基于递推随机子空间的电力系统低频振荡辨识

马燕峰，刘伟东，赵书强，范振亚

（1.华北电力大学 电力工程系，河北 保定 071003；2.国网天津市电力公司，天津 300072；3.国网内蒙古东部电力有限公司赤峰供电公司，内蒙古 赤峰 024000）

0 引言

近年来，我国电力系统发展迅速，虽然系统稳定性得到了显著提高，但电网结构中仍存在许多薄弱环节，低频振荡问题仍然对系统稳定性影响严重。智能电网的发展极大地推动了电力系统运行控制技术的提高，特别是广域测量系统（WAMS）的引入，为低频振荡的实时分析和控制提供了可能。

迄今为止，许多学者对低频振荡辨识技术进行了广泛的研究。目前，低频振荡辨识方法包括自回归移动平均（ARMA）、子空间、汉克总体最小二乘（HTLS）、Prony、矩阵束、频域分解（FDD）等参数化方法以及FFT、谱密度分析、维格纳维尔时频分布（WVD）、经验模态分解（EMD）、局部均值分解（LMD）等非参数分析方法［1-3］。

其中，Prony方法应用最为广泛和成熟。Prony算法将辨识信号表示成一系列具有任意幅值、相位、频率和衰减因子的复指数信号的线性组合，具有非线性的多位滤波特性。文献［4］深入分析了Prony方法的特点，对辨识中模型阶数和输入信号的选择问题进行了研究，结合实际WAMS测量系统建立了基于Prony方法的低频振荡辨识的实现方案。文献［5］指出Prony方法只能用于振荡信号（ringdowns）分析，提出了振荡信号的判定方法，实现了辨识过程中的辨识算法自动切换。

由于Prony方法一般用于暂态振荡信号辨识，但对于平稳运行时环境噪声激励下的稳态信号（ambient data）分析精度差。而实际WAMS记录的信号中含有大量的稳态信号，其中也蕴含了大量系统信息，更为充分有效地利用这些信号具有非常重要的意义。利用稳态信号进行辨识最早由文献［6］提出，随后众多谱分析方法用于该信号分析。近年来，ARMA分析方法在稳态信号分析中得到了广泛应用。文献［7］提出了采用自回归法对类噪声信号进行低频振荡模式辨识，从而实现电网正常运行状态下的动态稳定性预警。文献［8］提出了基于归一化峰度在常规ARMA法和高阶ARMA法之间自适应切换的低频振荡模式辨识，实现了对稳态噪声和动态数据的辨识。

子空间（subspace）算法包含随机子空间算法（SSI）、旋转矢量不变算法（ESPRIT）、N4SID算法、MOSEP算法等，这些算法将噪声子空间与信号子空间分离，识别精度高，抗噪能力强，适用于电力系统低频振荡的辨识。文献［9］将随机子空间方法应用于低频振荡辨识中，并采用改进稳定图技术实现了自动定阶。文献［10］提出了基于EMD和SSI的识别电力系统低频振荡模态参数的新方法，对于非线性非平稳的量测数据，首先通过EMD进行时空滤波和平稳化处理，得到本征模态函数（IMF）分量，再用SSI识别低频振荡参数。文献［11］提出利用子空间辨识电力系统降阶状态空间模型，辨识模型较为准确地识别出机电振荡模式。文献［12］提出了基于在线递推闭环子空间辨识的模型预测阻尼控制器的设计方法，通过辨识结果获得包含主导振荡模式的系统降阶状态空间模型。

由于传统SSI计算过程较为复杂，计算的时间复杂度较高，对逐点更新的WAMS数据，若逐采样点更新，则无法满足实时要求，只能使用块更新的方式进行计算，这样无法全面地展示系统状态的动态变化。针对该缺陷，与ARMA方法类似，SSI也可以采用逐点递推的方式从而可以极大地降低计算的复杂度，满足在线实时监视的要求。

文献［13］构造了基于协方差的随机子空间自适应递推方法，利用2台计算机分别采用不同遗忘因子递推并自适应切换，实现了递推平稳性与快速性配合，但这种方法需多个线程一起执行，且仅利用2个固定的遗忘因子，占用硬件资源大，同时灵活性和适应性差。

针对文献［13］中的缺点，本文采用递推随机子空间方法，实现低频振荡信息的实时提取。本文采用双边递推迭代方法实现递推过程，并根据低频振荡辨识信号的特点，制定了适合的遗忘因子和加权系数的选择策略，提高了递推抗噪声能力，并实现了平稳性和快速性二者间的平衡。

1 随机子空间基本原理

传统基于协方差的随机子空间中，n阶系统状态空间模型可以描述为［14］：

其中，状态向量 xk∈Rn；输出向量 yk∈Rm；系统矩阵A∈Rn×n；输出矩阵 C∈Rm×n；过程白噪声扰动向量 wk∈Rn；测量白噪声vk∈Rm。其中wk和vk满足互不相关的条件，即：

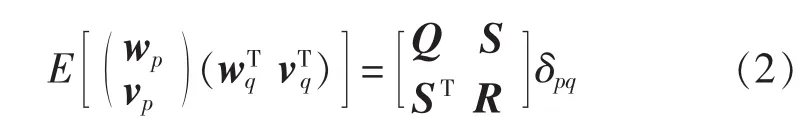
其中，E为数学期望算子；δpq为克罗内克函数，即当p=q 时 δpq=1，当 p≠q 时 δpq=0。

SSI辨识中首先构造Hankle矩阵：

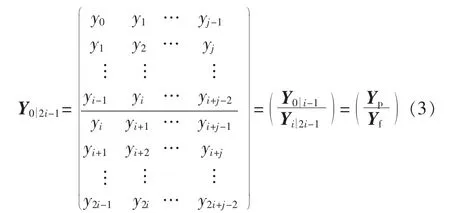
基于wk、vk为互不相关白噪声的假设，从而根据式（2）可以得到：

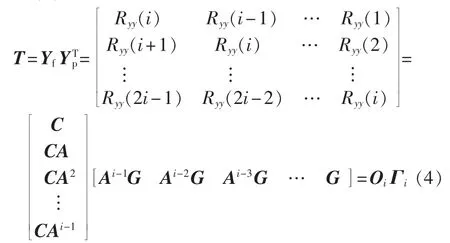
其中，Oi∈Rli×n为扩展可观测矩阵；Γi∈Rn×li为扩展可控矩阵；Ryy为相关函数为通道数；i为行数；j为列数。

对T进行SVD：

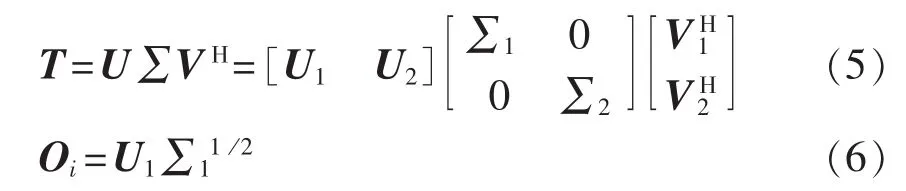
其中，U1、∑1、V1构成信号子空间，U2、∑2、V2构成噪声子空间，∑2相对于∑1要小很多；“H”表示转置。

模式、模态识别：

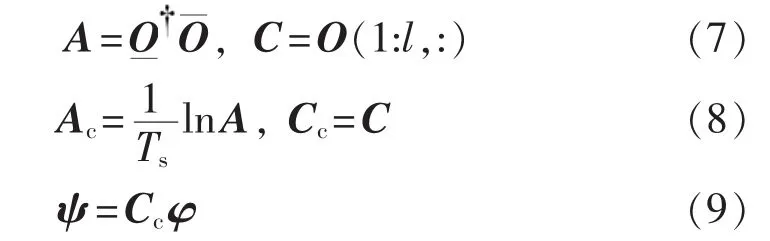
其中，A、C 为离散矩阵；Ac、Cc为连续矩阵Rl（i-1）×n为 O 去掉前 l行后的矩阵为 O 去掉后l行后的矩阵；Ts为采样时间；φ为-Ac特征分解的右特征向量；ψ为振型；“”表示伪逆。

2 子空间递推原理

子空间递推方法中主要包括梯度更新、投影更新等方法，其中较为熟知的有投影估计子空间跟踪算法（PAST）、压缩投影估计子空间跟踪算法（PASTd）、辅助变量投影子空间跟踪算法（PAST-EIV）、正交投影估计子空间跟踪算法（OPAST）、双边奇异值追踪（BI-SVD）、加权信息子空间（WINC）等方法。 文献［12］、［13］均采用了最为常用的 PAST-EIV，但 PASTEIV的正交性较差，本文并未采用该方法，而是采用了文献［15］提出的一种双边迭代的辅助变量子空间跟踪方法，其具体推导过程请参照该文献。对于其与PAST-EIV的性能对比，鉴于该文献中已经做了说明，本文将不再赘述，两者跟踪的结果大致相同，但相对于 PAST-EIV，其具有更低的算法复杂度和更好的收敛特性，且跟踪速度有所提高。

对第1节中T（t）采用如下的方式更新（类似于折息法最小二乘跟踪［16］）：

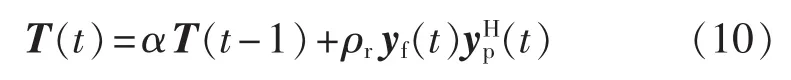
其中，α为遗忘因子；ρr为加权系数。

对T（t）进行SVD得到的右特征向量采用文献［15］提出的双边迭代方法进行更新，更新过程如下：

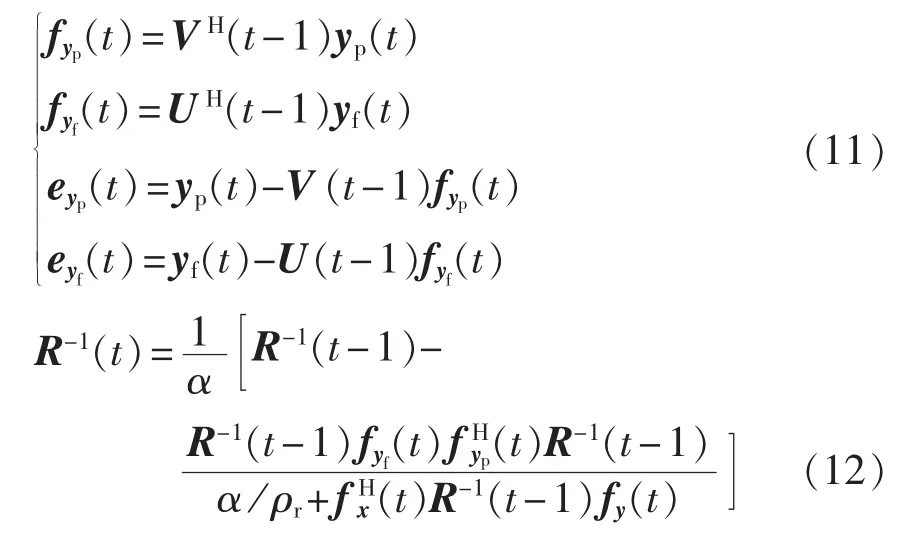
递推过程中唯一需要确定的2个参数是α和ρr，自适应地调整这2个参数对增强系统的鲁棒性非常重要。

以新息 eyf（t）作为衡量指标，当 eyf（t）突然急剧增大时，表明系统发生了变化，需要减小遗忘因子以加速遗忘，降低以前数据造成的影响，从而快速跟踪系统变化，当eyf（t）变化相对平稳时，表明系统变化目前相对平稳，应使遗忘因子尽量接近于1，以保证充分利用已有信息，保持递推辨识的平稳性。本文构建如下的自适应调整策略。

基于文献［17］中的统计方法，本文采用如下的方法测量新息 eyf（t）统计量：

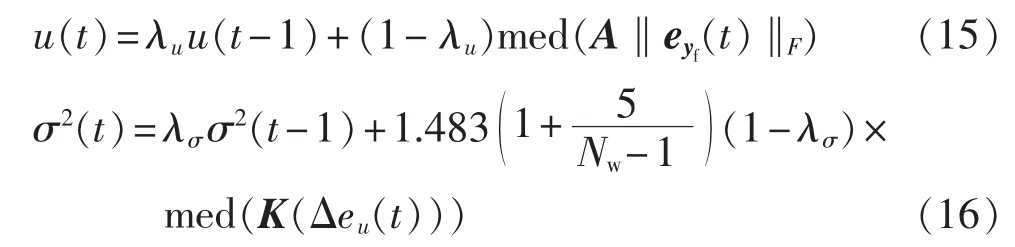
其中，u（t）为均值；σ（t）为方差；λu、λσ分别为相应的遗忘因子，一般取 0.9～0.99；K（x（t））=［x（t） x（t-1）… x（t-Nw+1）］；Δeu（t）=|‖e（t）‖F-u（t）|，‖·‖F为范数；Nw一般取5～11；med为求取中值。

根据获得的统计信息，采用Hampel函数自适应产生α：

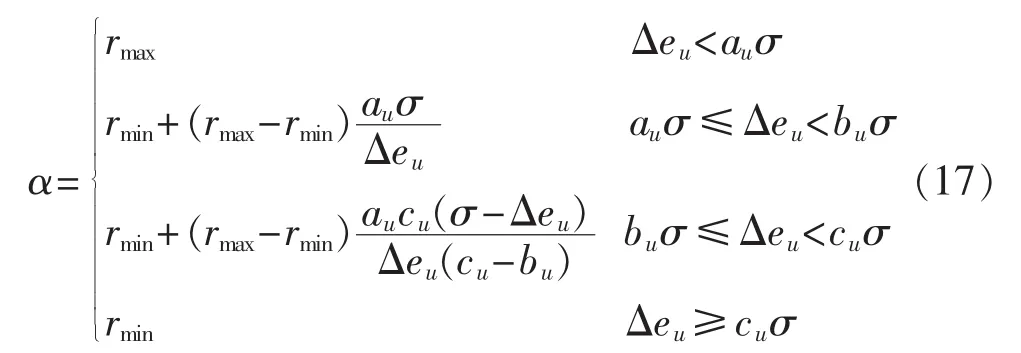
其中，rmax、rmin分别为设定的遗忘因子的最大值和最小值，本文取 rmax=1，au=1.5，bu=3.0，cu=4.5，rmax取 1可保证更新的渐进无偏性，而rmin需根据具体的采样速率确定合适值。

除系统变化引起新息eyf（t）突然增大外，冲击噪声也同样可以引起新息的增大，而引入ρr则是抑制冲击噪声引起的影响。ρr选用如下的形式：

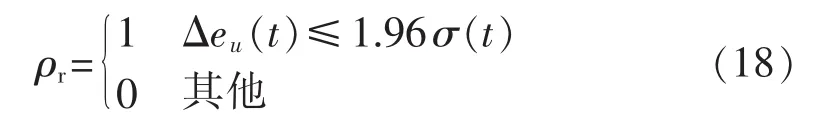
现在唯一的问题就是，怎样区分是冲击噪声还是系统变换引起的eyf（t）突然增大，本文采用了文献［17］提出的设置长度为Lw的缓冲区的思想，i0时刻eyf（t）突然增大，记录 U（i0-1）、V（i0-1）、R-1（i0-1），同时在接下来的Lw时间内，ρr保持为1不变，使上面提到的ρr机制暂停运行，如果是i0时刻系统变化引起的经过Lw次更新后新息均值u（i0+Lw）可以恢复到突变前的水平，如果是i0时刻仅是孤立的冲击噪声，那么经过Lw次更新u（i0+Lw）也可以恢复到突变前水平，如果u（i0+Lw）未恢复到正常，则表明Lw时间段内受到了多次冲击噪声影响，需要采用i0时刻前记录的 U（i0-1）、V（i0-1）、R-1（i0-1）重置 U、V、R-1后继续更新，i0+Lw后式（18）重新有效。

针对双边跟踪的特殊性，单个冲击噪声会影响2i次更新，缓冲区的长度将设为2i+Lw，同时考虑到遗忘因子不能仅作用于一次更新，这样的遗忘因子起不到实际作用，引用如下机制更新遗忘因子：

αr（t）=min（α（t），rααr（t-1）+（1-rα）） （19）其中，αr（t）为最终确定的遗忘因子；α（t）为式（17）确定的遗忘因子；rα为更新因数，取 0.9～0.99。 rα决定了最终遗忘因子恢复到rmax的速度，rα越小，则α（t）恢复越快遗忘能力越小，rα越大，则α（t）恢复越慢遗忘作用越强。当Δeu＜4.5σ时，认为系统中未受冲击噪声或者动态信号的影响，此时rα应选得小一些以保持更新的平稳性，而当Δeu≥4.5σ时，则表明系统很有可能发生了变化，rα选得大一些以加速遗忘作用，特别是动态信号发生后，应保持一定的遗忘能力，以避免幅值过高的动态信号对更新的影响，使更新保持良好的跟踪能力，基于上面的分析本文在Δeu＜4.5σ 时 rα取 0.9，Δeu≥4.5σ 时取 0.98。 同时，考虑到判据有可能在某些情况下失效，本文考虑引入均方根判据：

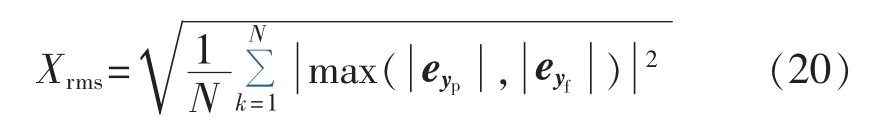
一旦Xrms＞ΓXth则也应判断为系统发生变化，应对遗忘因子进行修正，可置为rmin，Γ和Xth可由Xrms的统计特性得到，N可设为100。

结合低频振荡辨识中存在的实际问题，本文提出的遗忘因子和加权因子的选取策略如图1所示。

3 案例分析

3.1 理想系统

构造如下理想系统。

系统1：

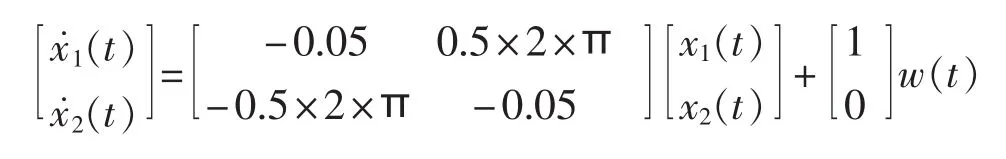
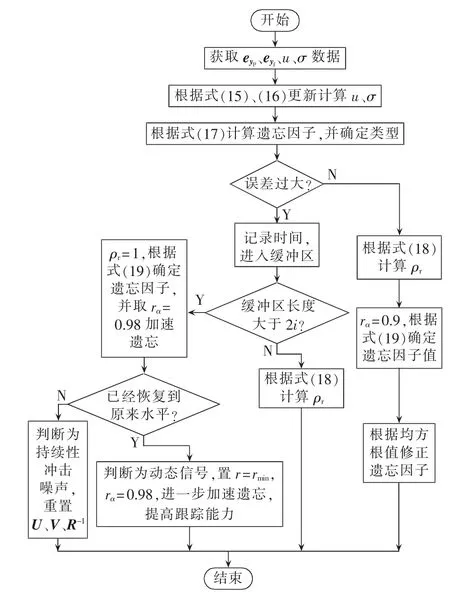
图1 遗忘因子和加权因子选取策略Fig.1 Strategy for selecting forgetting factor and weighting factor

系统2：

其中，w（t）为均值为0、方差为1的高斯白噪声序列。仿真过程中，从系统1突然切换到系统2。系统1理想频率和阻尼比分别为0.5 Hz和1.59%，系统2理想频率和阻尼比分别为 1 Hz和 1.59%，取信号 x1（t）为待辨识信号，选定跟踪阶数为2阶，子空间跟踪辨识结果如图2所示。

由图2（a）中可以看出系统在363 s进行了系统间切换。由图2（b）、（c）中可以看出,固定遗忘因子0.99 跟踪最快，而遗忘因子 0.995 和 0.998 则出现了较大的延迟，可见小遗忘因子可以保证跟踪的快速性，本文算法对切换系统的跟踪速度与固定遗忘因子 0.99 大体相近，但遗忘因子 0.995 和 0.998 相比0.99时的波动性要低，可见较大的遗忘因子可以保证跟踪的平稳性，而同固定遗忘因子0.998的跟踪结果相比，本文所提算法在平稳性方面仍略有优势，这点在阻尼比辨识结果中更为显著。同时，由阻尼比辨识结果可以看出，受200～300 s间相对较大的冲击性噪声影响，固定遗忘因子中由于未使用加权因子，对冲击性噪声的抗噪能力差，在冲击噪声影响下阻尼比变化很大，而本文算法中考虑了加权因子有效降低了冲击噪声的影响。本文所提算法能良好地跟踪系统变化，频率辨识结果与理想值吻合，阻尼辨识结果在理想值1.59%附近波动，误差在可接受范围内。

采用本文提出的递推更新辨识方法，提高辨识速度的同时，利用变遗忘因子和加权因子策略，在辨识的平稳性与快速性之间做出了相对的平衡，保证了辨识的鲁棒性。

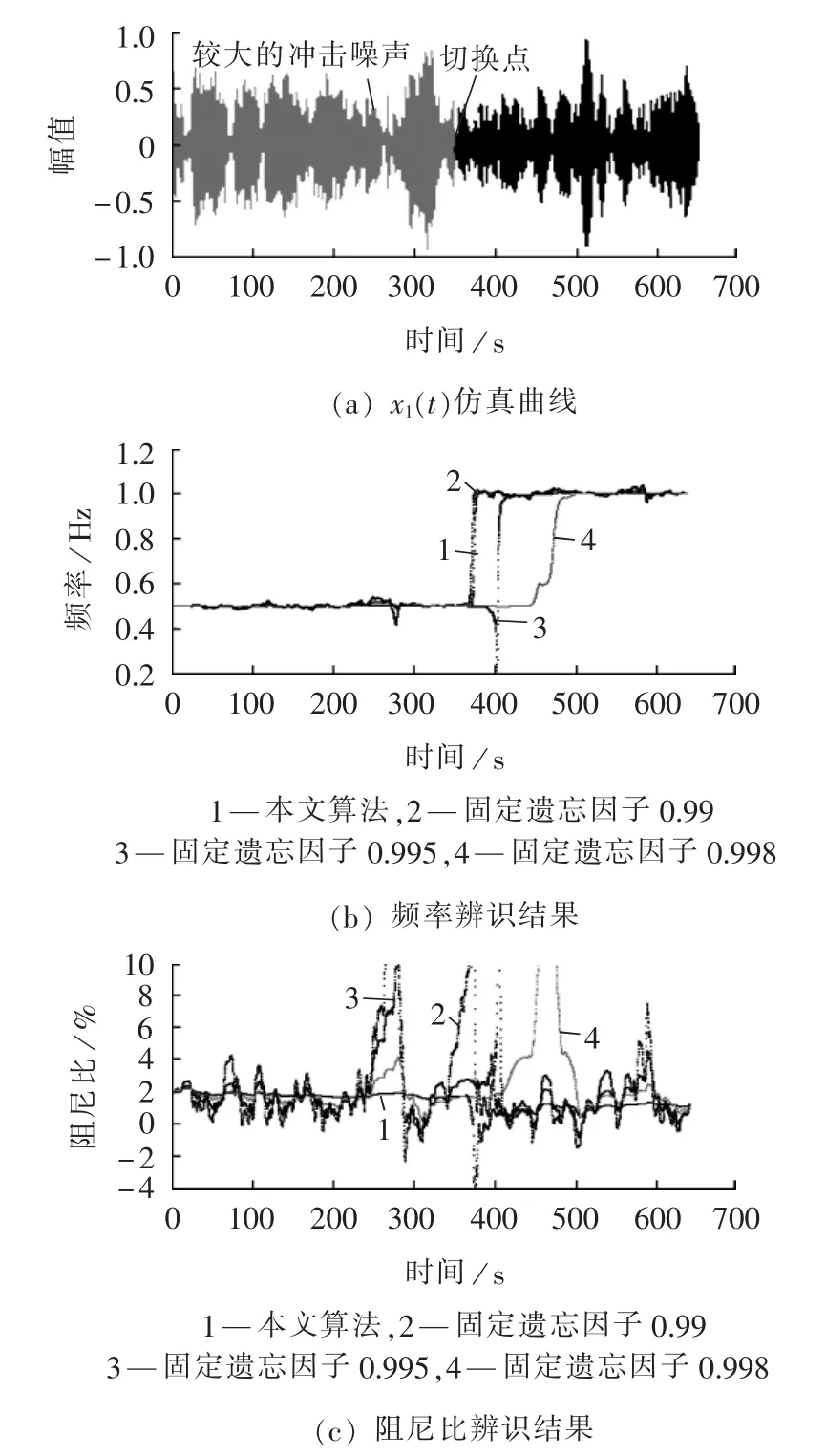
图2 理想系统辨识结果Fig.2 Identification results for ideal system

3.2 4机2区系统仿真

采用 PST（Power System Toolbox）仿真工具，调节4机2区系统参数，在负荷中加入方差为0.05的高斯噪声进行仿真，并在仿真中设置地区一负荷节点突然失去负荷500 MW，其不平衡功率由各机组平均分配，失负荷前后系统小干扰稳定分析结果如表1所示。

本文根据文献［9］提出的方案，离线确定递推阶数为4，选定阶数后在此基础上进行递推更新，其更新结果如图3所示，图中功率为标幺值。

对比故障前PST中小干扰分析结果与辨识得到的结果可以看出，频率辨识的结果基本相同，阻尼结果存在一定波动，但对于区间主导模式对应的阻尼辨识结果与小干扰分析结果一致，并在其附近波动，且相对平稳，对于信号较弱的地区模式，其阻尼比变化相对较大，阻尼辨识结果较差，故障后由于遗忘因子调整机制的作用，算法在很短的时间内，跟踪收敛到了新的模式下，收敛过程快速稳定，同时由于充分利用了动态信号的作用，使得故障后的阻尼比变化更为平滑。

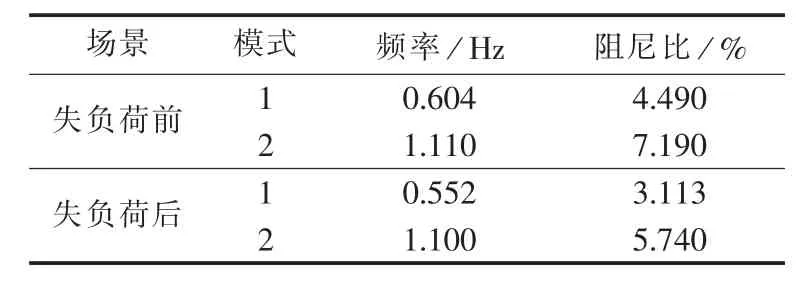
表1 4机2区系统PST小干扰稳定分析结果Table 1 Results of small disturbance stability analysis by PST for 4-generator 2-area system

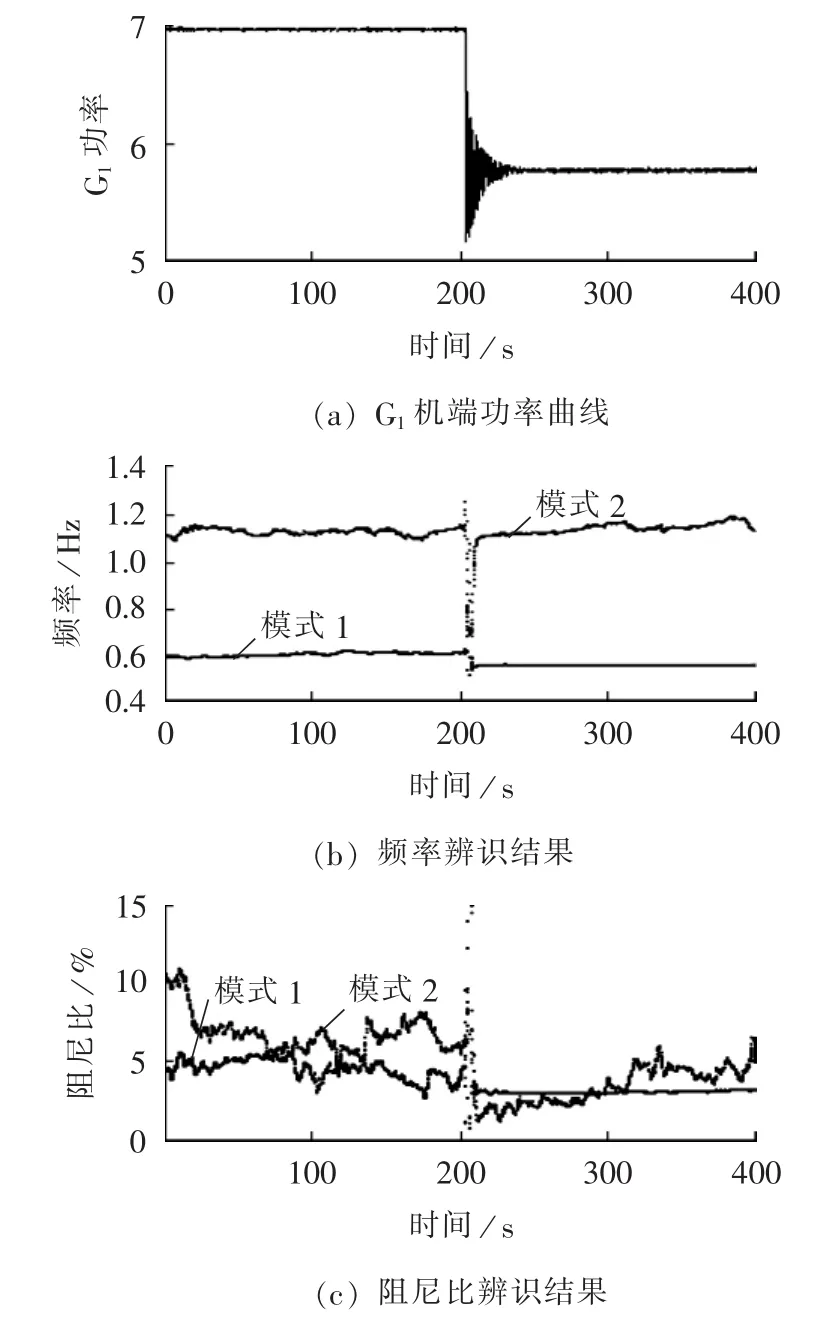
图3 4机2区系统仿真辨识结果Fig.3 Identification results for 4-generator 2-area system

3.3 PMU数据

3.3.1 NASPI-2104-Workshop-Oscillation-Case2［18］

采用NASPI Oscillation-Case2中线路2-1的电流幅值作为待辨识数据，选取起始52 s环境激励数据作为SSI分析,离线确定阶数为4，但递推跟踪中考虑实际数据中非振荡分量较多，采用8阶进行递推更新350 s数据，其递推更新结果如图4所示。

递推辨识中前180 s存在0.31 Hz和0.88 Hz左右2个模式，二者阻尼比均相对较高，系统稳定，180 s（对应NASPI数据232 s）左右出现明显的1.25 Hz振荡，188 s（对应 NASPI数据 240 s）时 2.5 Hz频率分量趋于稳定，二者阻尼均降为0。1.25 Hz振荡阻尼比为0，与系统中发生1.25 Hz共振振荡相吻合，可通过NASPI提供的案例参考结果验证本文结果［18］，并与ABB等公司的辨识结果对比分析。

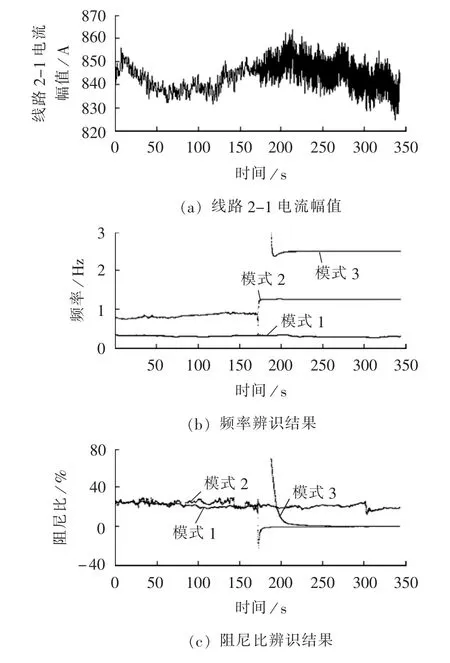
图4 NASPI数据辨识结果Fig.4 Identification results for NASPI data

3.3.2 某电厂实测WAMS数据

图5（a）为某电厂实测得到的WAMS数据，去均值处理后的功率波动情况，机组运行53.25 s时发生瞬时性单相短路故障，造成WAMS数据在53.25～54.65 s产生了冲击性噪声，针对此WAMS数据跟踪辨识结果如图5所示。

通过对WAMS数据辨识分析可以看出，该机组主要参与了0.5 Hz和1.1 Hz左右的2个振荡模式，其中0.5 Hz振荡模式阻尼较强，而1.1 Hz振荡模式阻尼较弱，瞬时性单相短路故障后，1.1 Hz模式阻尼减弱到5%左右，运行人员需要关注此振荡模式。计算机采用2.5 GHz双核处理器，实现了5000余次更新仅用时3.3s，而普通随机子空间方法实现此计算需用时100 s以上，相比较而言，递推方法极大地降低了时间复杂度，同时更能有效地体现出模式信息的动态变化过程。

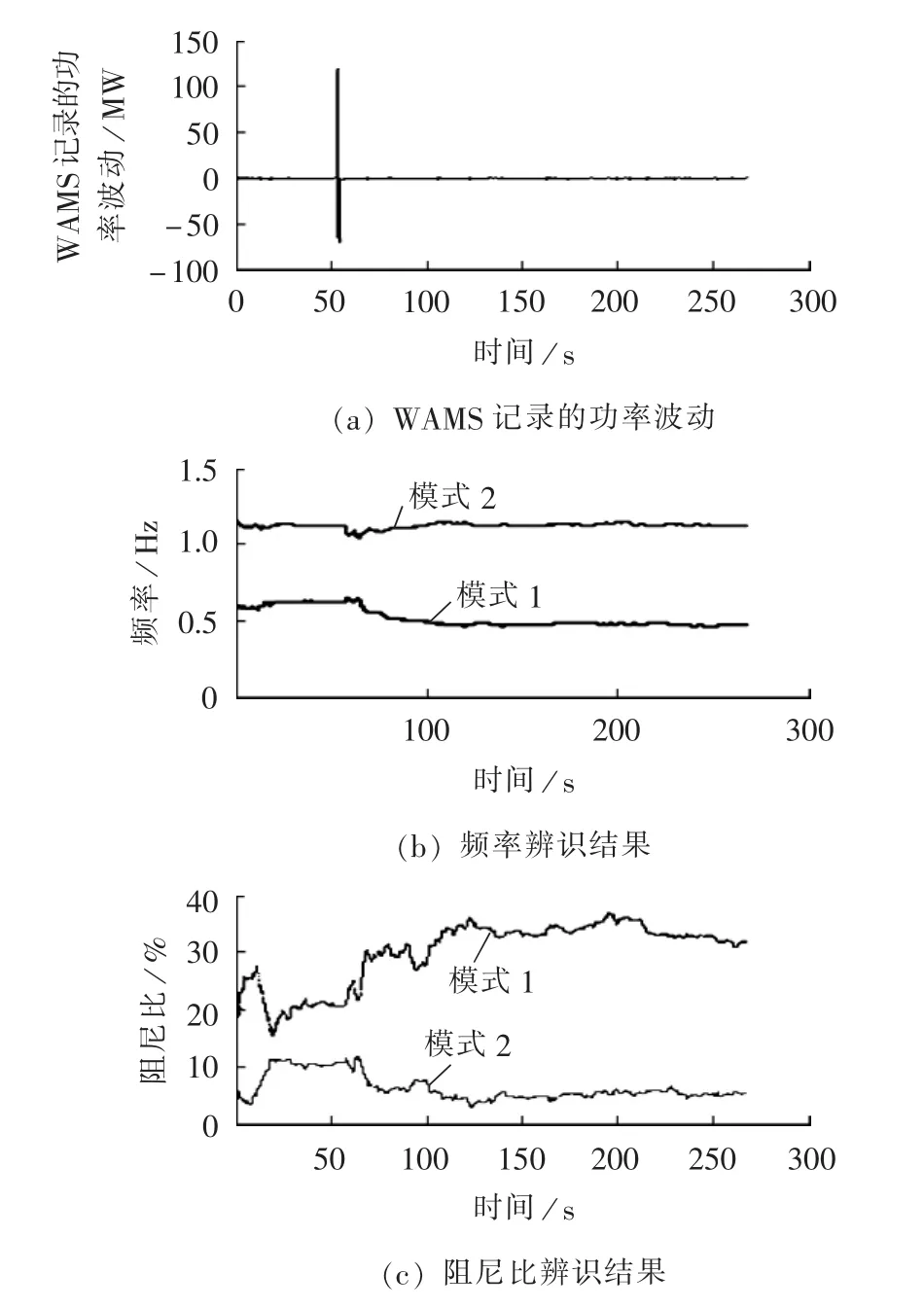
图5 WAMS数据辨识结果Fig.5 Identification results for WAMS data

4 结论

本文基于随机子空间方法，实现低频振荡的实时在线递推辨识，采用递推方式更新降低了低频振荡辨识的时间复杂度，使随机子空间可以有效地进行在线应用。本文基于低频振荡数据类型的特点，提出了兼顾递推平稳性与快速性的遗忘因子和加权因子确定策略，更能有效地抑制冲击性噪声的影响。

遗忘因子和加权因子是递推更新中极为重要的2个参数，能直接决定递推更新的效果。准确的数据类型判别对2个参数的确定具有举足轻重的作用，本文主要利用了更新新息作为判断标准确定这2个参数，显然有些不足，依靠其他数据特征和故障检测方法，对低频振荡数据类型做进一步的分类需要更为细致的研究，同时针对递推辨识的平稳性和跟踪快速性这对相互矛盾的性能，结合低频振荡数据类型特点提出更为有效的参数选取策略或者更为鲁棒的跟踪算法也是亟待详细研究的方面。

参考文献：

［1］高洁，李群湛，汪佳，等.基于NExT-ERA与SSI-DATA环境激励下的低频振荡辨识方法比较［J］.电力自动化设备，2016，36（1）：89-95.GAO Jie，LIQunzhan，WANG Jia，etal.Comparison oflowfrequency oscillation identification between NExT-ERA and SSIDATA ambient excitation methods［J］.Electric Power Automation Equipment，2016，36（1）：89-95.

［2］汪颂军，刘涤尘，廖清芬，等.基于EEMD-NExT的低频振荡主导模式工况在线辨识与预警［J］. 电力自动化设备，2014，34（12）：111-116.WANG Songjun，LIU Dichen，LIAO Qingfen，et al.Online dominant mode identification and warning based on EEMD-NExT for low frequency oscillation in operating conditions［J］.Electric Power Automation Equipment，2014，34（12）：111-116.

［3］吴超，陆超，韩英铎，等.Prony方法和ARMA法在低频振荡模式辨识中的适用性比较［J］.电力自动化设备，2010，30（3）：30-34.WU Chao，LU Chao，HAN Yingduo，et al. Comparison of applicabilityin low frequency oscillation mode identification between Prony and ARMA［J］.Electric Power Automation Equipment，2010，30（3）：30-34.

［4］鞠平，谢欢，孟远景，等.基于广域测量信息在线辨识低频振荡［J］.中国电机工程学报，2005，25（22）：59-63.JU Ping，XIE Huan，MENG Yuanjing，et al.Online identification of low-frequency oscillations based on wide-aera measurments［J］.Proceedings of the CSEE，2005，25（22）：59-63.

［5］ZHOU Ning，HUANG Zhenyu，TUFFNER F，etal.Automatic implementation ofProny analysisforelectromechanicalmode identification from phasor measurements［C］∥Power and Energy Society General Meeting.Minneapolis，USA：IEEE，2010：1-8.

［6］PIERRE J W，TRUDNOWSKI D J，DONNELLY M K.Initial results in electromechanical mode identification from ambient data［J］.IEEE Transactions on Power Systems，1997，12（3）：1245-1251.

［7］吴超，陆超，韩英铎，等.计及模型定阶的低频振荡模式类噪声信号辨识［J］.电力系统自动化，2009，33（21）：1-6.WU Chao，LU Chao，HAN Yingduo，et al.Power system oscillation modes estimation based on ambient signals considering model order selection［J］.Automation of Electic Power Systems，2009，33（21）：1-6.

［8］徐玉韬，卢继平，陈刚，等.稳态和动态混合信号的在线低频振荡模式辨识方法［J］.电力系统自动化，2012，36（2）：31-35.XU Yutao，LU Jiping，CHEN Gang，et al.An online low frequency oscillation estimation method for ringdowns signals mixed ambient data［J］.Automation of Electic Power Systems，2012，36（2）：31-35.

［9］赵书强，张一，马燕峰.基于数据驱动随机子空间方法在低频振荡辨识中的应用［J］.电力系统保护与控制，2013，41（8）：81-86.ZHAO Shuqiang，ZHANG Yi，MA Yanfeng.Data-drivenbased stochastic subsapce indentification for low frequency oscillation analysis［J］.Power System Protection and Control，2013，41（8）：81-86.

［10］蔡国伟，杨德友，张俊丰，等.基于实测信号的电力系统低频振荡模态辨识［J］.电网技术，2011，35（1）：59-65.CAI Guowei，YANG Deyou，ZHANG Junfeng，et al. Mode identification of power system low-frequency oscillation based on measured signal［J］.Power System Technology，2011，35（1）：59-65.

［11］郝正航，陈卓，李少波，等.子空间法在小干扰稳定分析及协调控制中的应用［J］.电工电能新技术，2007，26（3）：20-23.HAO Zhenghang，CHEN Zhuo，LIShaobo，etal.Small-signal stability analysis and coordinated control based on subspace algorithm［J］.Advanced Technology of Electrical Engineering and Energy，2007，26（3）：20-23.

［12］叶华，刘玉田.基于在线递推闭环子空间辨识的模型预测阻尼控制［J］.中国电机工程学报，2009，29（28）：55-61.YE Hua，LIU Yutian.Model predictive damping control based on on-line recursive closed-loop subspace identification［J］.Proceedings of the CSEE，2009，29（28）：55-61.

［13］NEZAM S S A，VENKATASUBRAMANIAN V.Electromechanical mode estimation using recursive adaptive stochastic subspace identification［J］.IEEE Transactions on Power Systems，2014，29（1）：349-358.

［14］VAN OVERSCHEE P，DE MOOR B.Subspace identification theory implementation application［M］.Amsterdam，Holland：Kluwer，1996：95-134.

［15］朱从光，冯大政，聂卫科.辅助变量双迭代子空间追踪［J］.制导与引信，2007，28（2）：42-46.ZHU Congguang，FENG Dazheng，NIE Weike. Bi-interation subspace tracking using instrumental variable［J］.Guidance&Fuze，2007，28（2）：42-46.

［16］萧德云.系统辨识理论及应用［M］.北京：清华大学出版社，2014：124-126.

［17］CHAN S C C，WEN Y，HAO K L.A robust past algorithm for subspace tracking in impulsive noise［J］.IEEE Transactions on Signal Processing，2006，54（1）：105-115.

［18］NASPI Oscillation Detection and Voltage Stability Tools Technical Workshop Meeting.Houston，TX ［EB／OL］.（2014-10-22）［2015-05-20］.https：∥www.Naspi.org／site／Module／Meeting／Forms／General.spx?m_ID=MEETING&meetingid=347.