空间耦合粒子群优化算法及峰谷电价下IES-CCHP区域联合调度
2016-05-22周任军晁岱旭李新军刘嫣然
周任军,晁岱旭,李新军,刘嫣然,许 阳,孙 洪
(长沙理工大学 智能电网运行与控制湖南省重点实验室,湖南 长沙 410114)
0 引言
在能源需求大幅增长与环境保护日益迫切的双重压力下,综合能源系统IES(Integrated Energy System)将成为未来30~50年能源领域的主要承载形式[1]。伴随节能减排政策的促进以及天然气成本的降低,冷热电联供CCHP(Combined Cold Heat and Power)技术作为区域供冷/热系统已得到示范和推广[2-3]。其研究以热能的综合梯级利用为主线,考虑系统的经济性以及用户的电力需求,遵循冷热电联产系统的集成原则[4];为考虑天然气与电力系统之间的相互影响,研究了考虑天然气管道运行约束的电力风险评估[5]和风电随机性的电力机组日前调度[6]。这些研究或重点考虑电力、热力系统联合,或考虑电力、天然气联合,但均未综合考虑其三者的联合,然而这却是在IES背景下能源领域最受关注的关键技术。同时作为IES中的主要能源网络,电/气/热转换环节是通过CCHP机组实现的,通过利用CCHP输出与输入间的能源集线器模型[7],能够刻画出电力、天然气和热力系统间的交互影响。
CCHP接入电网运行时既从主网购电,又可以向主网售电。为获得最优经济效益将响应分时电价改变其供能方案[8],尤其是购售电交易计划。而峰谷电价能激励用户积极参与削峰填谷[9],达到需求侧管理的目的。目前,峰谷定价问题主要针对只消耗电能的一般电力用户[10-11],对于CCHP这类具有灵活调节供能方案的用户鲜见报道。为此,在传统考虑燃料成本和排放污染气体所产生的环境成本的基础上,计及峰谷电价下的购售电成本不仅能够使CCHP参与需求侧管理,而且能促使其获得更大的经济效益。
近年来,粒子群优化PSO(Particle Swarm Optimization)算法由于其快速、简便的优点已广泛应用于函数优化、神经网络训练、组合优化、模式识别、电力系统优化等领域[12-13]。随着融入改进的混沌策略[14]、采用自适应变异算子的自调节[15]、随机黑洞处理与聚类[16]等方法引入了全局搜索信息,为其增加了解的多样性,在一定程度上改善了过早收敛的缺陷。但优化效率低,效果不太令人满意。一种改进的空间粒子群优化SPSO(Space Particle Swarm Optimization)算法通过高度参数的引入[17],与速度、位置共同组成一个三维寻优参数空间,促使粒子改变寻优视角,改善了局部最优问题。然而多维空间并不同于二维平面,粒子的寻优方向随机性很大。为了有效地将每个粒子每一维参数彼此联系起来,使所有参数从总体上同时趋向最优解,达到将寻优视角指向全局极值点的目的,引入了一种耦合协调数学模型,提出空间耦合粒子群优化SC-PSO(Space-Coupling Particle Swarm Optimization)算法。
1 峰谷电价下IES-CCHP区域联合环保经济调度模型
1.1 CCHP能源集线器模型
在IES中,可用能源集线器来描述其中的能源转换关系,其基本结构如图1所示。典型的CCHP能源集线器模型由电力变压器、微型燃气轮机MT(MicroTurbine)和燃气锅炉 GB(Gas Boiler)共同构成。图中,输入环节包括电能和天然气,其中电能直接输入变压器,而天然气同时输入微型燃气轮机和燃气锅炉;输出环节包含了电力和冷热能两部分,其中所输出的电能由变压器和微型燃气轮机供给,而所输出的冷热能则由燃气锅炉和微型燃气轮机共同产生。由此可得如式(1)所示的多输入多输出的功率转换关系式,其中的耦合系数不仅与转换装置的转换效率有关,还与能源在不同转换装置中的分配比例有关,因此引入分配系数 νMT(0≤νMT≤1),则 νMTPg表示输入微型燃气轮机中的天然气,(1-νMT)Pg表示输入燃气锅炉中的天然气。

其中分别为天然气经过微型燃气轮机转化为电力和热能的转换效率;ηT为变压器效率;ηGB为燃气锅炉的制冷和制热的能效比;Pe和Pg分别为CCHP与电网和天然气网络的能量交互值;Le和Lh分别为CCHP所供应的电负荷和热负荷。

图1 能源集线器典型结构Fig.1 Typical structure of energy hub
1.2 峰谷电价下CCHP的购售电成本f1
峰谷电价能够激励用户积极参与削峰填谷。峰谷定价时,CCHP系统较统一电价所得经济效益是激励其调节用能的主要动力。因此CCHP系统为获取最大经济效益将响应电价改变其供能方案,尤其是购售电交易计划。购售电成本受电价和购售电功率的相互影响,包括买电带来的成本和卖电带来的收益。
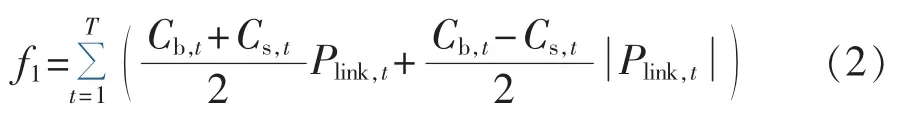
其中,Cb,t、Cs,t分别为时段 t购电和售电的价格;Plink,t为CCHP系统在时段t的购售电功率,为正表示CCHP系统向电网买电,为负表示向电网售电;T为总时段数。
1.3 燃料成本模型f2
系统总燃料花费f2(单位为$)可表示为:
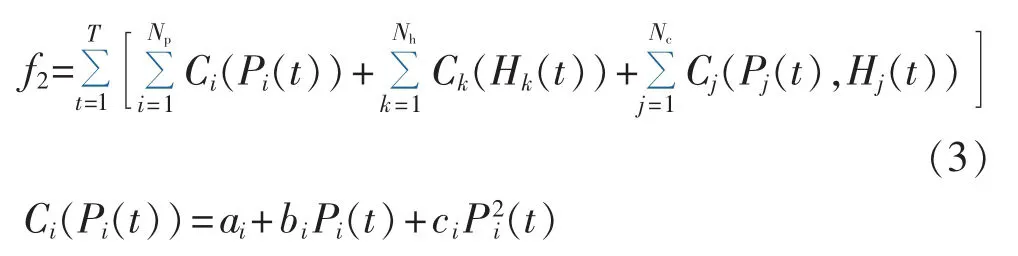
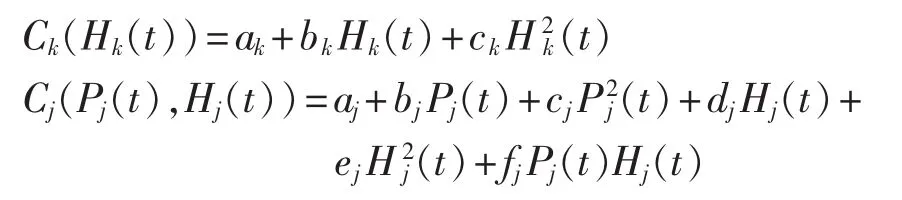
其中,Ci(Pi(t))为第 i台发电机组在时段 t产生的燃料成本(单位为 $);Ck(Hk(t))为第 k 台供冷热机组在时段 t产生的燃料成本(单位为 $);Cj(Pj(t),Hj(t))为第j台CCHP机组在时段t内产生的燃料成本(单位为 $);aj、bj、cj、dj、ej、 fj为第 j台机组的燃料消耗函数系数;Np、Nc、Nh分别为仅发电、CCHP 和仅供冷热机组的台数。
1.4 环境成本模型f3
(1)仅发电机组部分。
仅发电机组在时段t内产生的环境成本ft31(单位为$)可表示为:

(2)仅供冷热机组部分。
仅供冷热机组在时段t内产生的环境成本ft32(单位为$)可表示为:

(3)CCHP机组部分。
CCHP机组在时段t内产生的环境成本ft33(单位为$)可表示为:
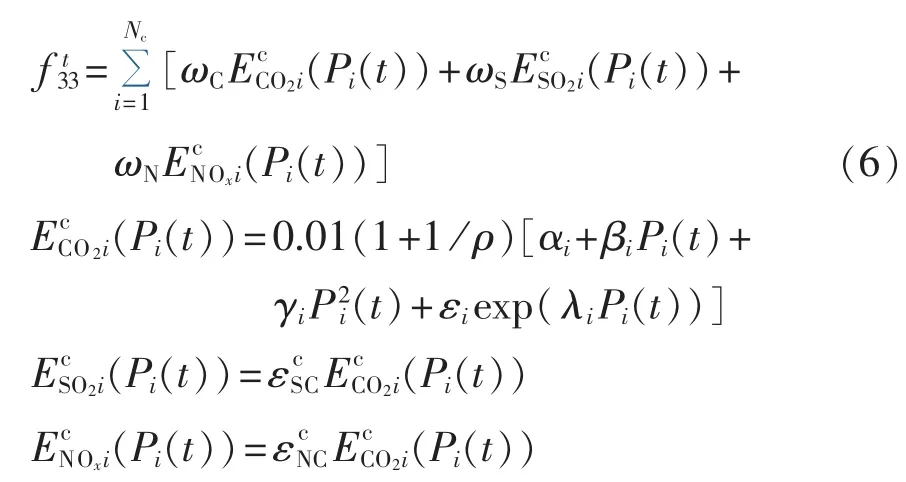
综上所述,系统在整个调度时段T内产生的环境总成本f3(单位为$)为:
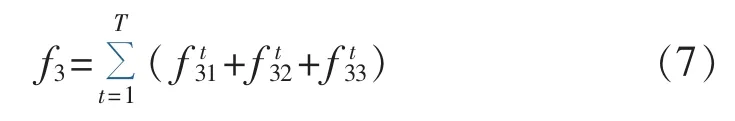
其中,ωC、ωS、ωN分别为 CO2、SO2、NOx单位排放量所对应的环境价值与污染排放罚款之和分别为第 i台仅发电机组的CO2、SO2、NOx排放模型(单位为 t/h);αi、 βi、λi、γi、εi为第i台机组的CO2气体排放参数;ρ为供热当量性能系数[10]为仅发电机组部分的碳排放折算系数分别为第 i台 CCHP 机组的 CO2、SO2、NOx排放模型(单位为t/h)为 CCHP 机组部分的碳排放折算系数;分别为第 i台仅供冷热机组的 CO2、SO2、NOx排放模型(单位为 t/h);为仅供冷热机组部分的碳排放折算系数。
1.5 IES-CCHP联合环保经济调度模型
1.5.1 目标函数
IES-CCHP环保经济优化调度的目标是,在整个调度时段T内,在满足CCHP能源集线器模型的条件下,使系统购售电成本、燃料成本与环境成本之和达到最小值。因此,其优化目标函数可表示为:
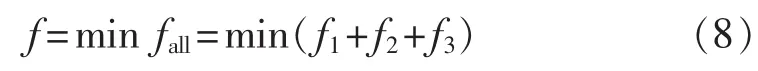
其中,f为系统的综合成本;f1、f2和 f3分别如式(2)、式(3)、式(7)所示。
1.5.2 约束条件
(1)购售电功率约束。

其中分别为CCHP系统在时段t购售电功率的最小值和最大值。
(2)各机组出力约束。
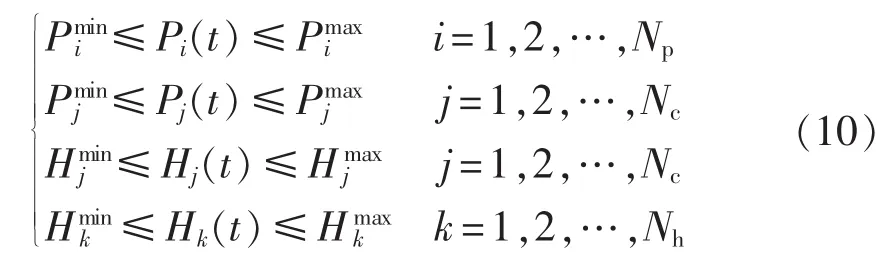
(3)系统功率平衡约束。
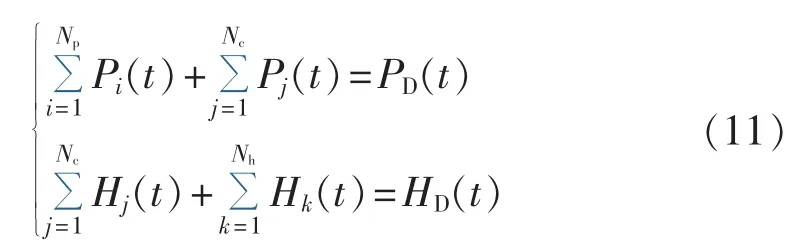
其中,PD(t)、HD(t)分别为时段 t的总电负荷和总热负荷。
(4)系统许可的污染气体排放约束。

其中,ECO2i、ESO2i、ENOxi(i=1,2,…,N)分别为第 i台机组排放 CO2、SO2、NOx的总量;ECz、ESz、ENz分别为 CO2、SO2、NOx的配额排放量;N为系统总机组数。
2 耦合协调函数
2.1 耦合意义及模型
耦合具有多方面的意义[18]:物理学指2个或2个以上的系统或运动方式之间通过各种相互作用而彼此影响以致联合起来;电子学中指能量从一种介质(例如一根金属线、光导纤维)传播到另一种介质的过程,是一种能量传递过程;概率论中耦合被认为是关联结构,是一种处理统计中随机变量相关性问题的方法;从经济学意义来看,耦合是为了降低耗费、提高效率。
借用耦合度函数,可以揭示n个(不失一般性,假设n=3)目标函数彼此之间相互作用、相互影响的内在协同机理。耦合度函数表示为:
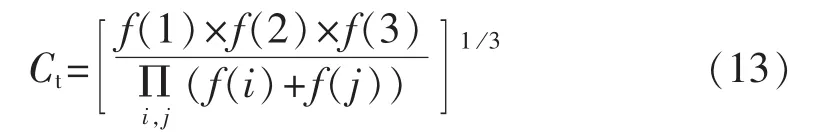
其中,i,j=1,2,3,i≠j;Ct为耦合度,取值范围为[0,1]。Ct值越大,表明耦合度越好,说明系统之间有序配合,紧密相关。
2.2 耦合协调模型
耦合度函数的缺点是仅仅能够描述系统之间协调发展的程度,但是无法确定系统是在较高的水平上相互促进,还是在较低的水平上紧密联系。因此,进一步引入耦合协调函数,不仅能够反映系统之间的协调程度,还能体现协调发展水平的阶段性。耦合协调度可表示为:

其中,R为耦合协调度;Tt为综合评价指数,可由式(15)表示。

其中,α、β、γ 为权重系数,分别表示 f(1)、f(2)、f(3)的贡献量,且有 α+ β+γ=1。
R值越大,反映了系统之间在高水平上相互协调。 本系统中 f(1)、 f(2)、 f(3)的贡献量一样,令α=β=γ=1/3。按照耦合协调度的大小可以划分不同耦合协调发展阶段。设定耦合协调度R,当0<R<0.3时,为低级耦合协调发展阶段;0.3≤R<0.5时,为中级耦合协调发展阶段;0.5≤R<0.8时,为高级耦合协调发展阶段;0.8≤R<1时,为极度耦合协调发展阶段。
3 SC-PSO算法
3.1 SPSO算法及其高度参数
在PSO算法中,每个优化问题的未知解都可以作为搜寻范围内的一个点,即粒子。每个粒子都对应一个取决于待优化函数的适应度值。所有粒子移动的方向和距离都是由其速度决定的,并且群体中的所有粒子均跟随最优粒子在一个平面解域内搜寻。每次速度和位置的更新原则分别如式(16)、(17)所示。
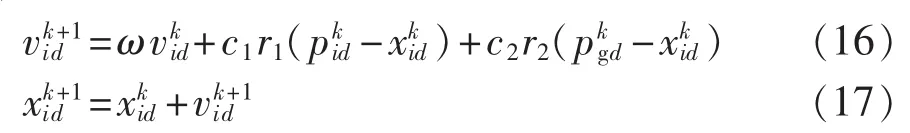
其中,i=1,2,…,m,m 为种群规模;d=1,2,…,D,D为待优化变量的个数;c1和c2为学习因子分别为粒子i对应第d个待优化变量在第k次、第k+1次修正时对应的速度分别为粒子i对应第d个变量在第k次、第k+1次修正时对应的位置为粒子i对应第d个待优化变量在第k次修正时个体最优位置为整个群体对应第d个变量在第k次修正时全局最优位置;r1、r2为介于0与1之间均匀分布的随机数;ω为惯性权重。
SPSO算法通过对每个粒子优化变量矩阵的每一分量附加一组高度参数,使得每个待优化变量在由位置x、速度v和高度h组成的全新参数空间域内寻优,即x-v-h空间。其寻优过程就像在绵延山群中,站在每个山腰均容易得到所在山头极值点,通过增加一维高度参数的扰动,能促使粒子改变寻优视角,便于寻求整个山脉的最高处。此时,位置xij的修正方式发生了变化,按式(18)来更新。

其中为粒子i对应第j个变量在第k+1次修正时对应的高度。
高度参数h的具体修正格式如式(19)所示。
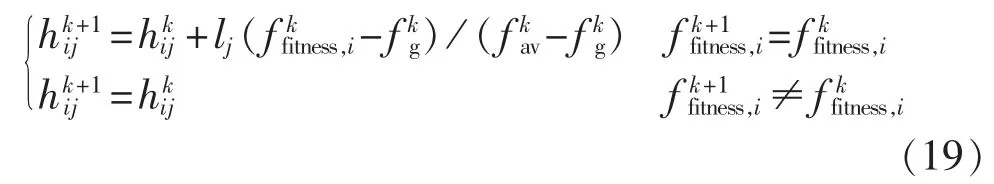
其中为粒子i在第k次修正时所对应的适应度值;lj为第j个变量对应的可行区间的长度为所有粒子在第k次修正时所对应的最优适应度值为所有粒子在第k次修正时所对应的平均适应度值。
3.2 SC-PSO算法
多维空间并不同于二维平面,粒子的寻优方向随机性很大。从式(16)和式(19)可看出,速度v和高度h每次更新时都是按照各自的方式进行的。而x、v和h三者每次更新时相互影响的关系并不能看出来。为此在构成的全新的三维空间里引入上述耦合协调模型如式(13)所示,有效地将每个粒子每一维参数彼此联系起来,使所有参数从总体上同时趋向最优解,达到将寻优视角指向全局极值点的目的。进而,探索一种新型的SC-PSO算法。由于速度v是时间的函数,此SC-PSO算法不仅体现了空间上的联系,而且从时间尺度上也进行了一定关联。
另一方面,从PSO算法的内部运动来看,当群体中的所有粒子对应的每一维参数变量跟随最优粒子对应的参数在一个全新的空间解域内搜寻时,可有效地将每一维参数变量彼此联系起来,从而使所有参数从总体上同时趋向最优解,而不是杂乱分裂地仅根据每一维参数变量的最优解进行毫无目的和联系的寻优。SC-PSO算法不仅提高了全局收敛性,而且从根本上减少了算法的无效路径,提高了效率,大幅降低了随机性。
4 算例仿真结果分析
4.1 算例与参数处理
以某地方的IES-CCHP系统为例,其中输入环节包括电能和天然气;负荷包含电负荷、热(冷)负荷,系统各时段电、热(冷)负荷需求如图2所示;各发电机的基本参数如表1所示,其中 G1、G2、G3、G4为仅供电机组,C5和C6为CCHP机组,H7为仅供冷热机组;取粒子种群规模m=40,学习因子c1和c2均取1.5,惯性权重取ωmax=0.9、ωmin=0.4,R取高级耦合阶段指标0.85,最大迭代次数为100次,初始惩罚系数μ取100;CO2排放参数如表2所示;SO2排放参数如表3所示;NOx排放参数如表4所示;按电力行业排放标准设定各类污染气体单位排放量的环境价值与相应罚款如表5所示;某地CCHP峰谷电价如表6所示。
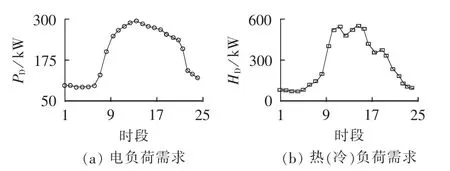
图2 电和热负荷需求情况Fig.2 Electricity and heat demands
4.2 仿真结果分析
为了对比明显,选取负荷需求最大的时段进行对比分析,此时电负荷为293 kW,热负荷为548 kW。针对上述案例分别采用PSO算法、SPSO算法和SC-PSO算法进行优化,三者优化过程对比见图3。
从图3中可以看出,SC-PSO算法在一定程度上比SPSO算法更好地缓解了PSO算法容易陷入局部最优且难跳出来,导致过早收敛的缺陷。在收敛性能方面,PSO算法在迭代不到10次就陷入了局部最优而且不能自我调整跳出局部最优区域;SPSO算法虽然在前面部分跳出了局部最优区域,但是也在不到50次迭代又陷入了新的局部最优;而SC-PSO算法出现了非常明显多次自我调整的现象,跳出局部最优区域,而且也在寻优不到60次就找到了全局最优解,获得了更好、更精确的目标值,这也进一步展现了其良好的收敛特性和高效稳定的寻优性能,较好地解决PSO算法容易陷入早熟且难跳出局部最优区域的缺陷。这是由于SC-PSO算法通过引入耦合协调模型,有效地将每个粒子的每一维变量彼此联系起来,使所有变量从总体上同时趋向最优解,从而使得粒子易于跳出局部最优区域,同时也避免了其他跟随的粒子陷入局部最优,提高了全局收敛性和效率,增强了全局寻优能力。对于该时段,在同等条件下分别对各算法独立计算50次,得到其优化结果分布图如图4所示。
从图4中可以看出:SC-PSO算法优化结果的随机性明显小于SPSO算法优化结果的随机性;对50次独立计算的结果取平均值,可得各自的该时段综合成本优化结果如表7所示。

表1 CCHP机组参数Table 1 Parameters of CCHP units
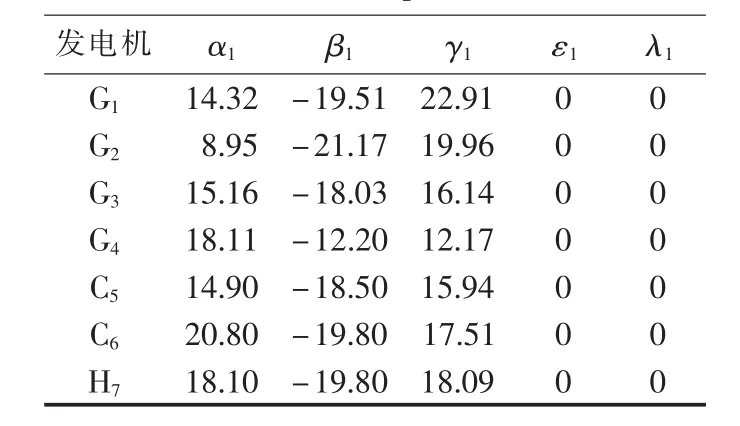
表2 各机组CO2排放参数Table 2 CO2emission parameters of units
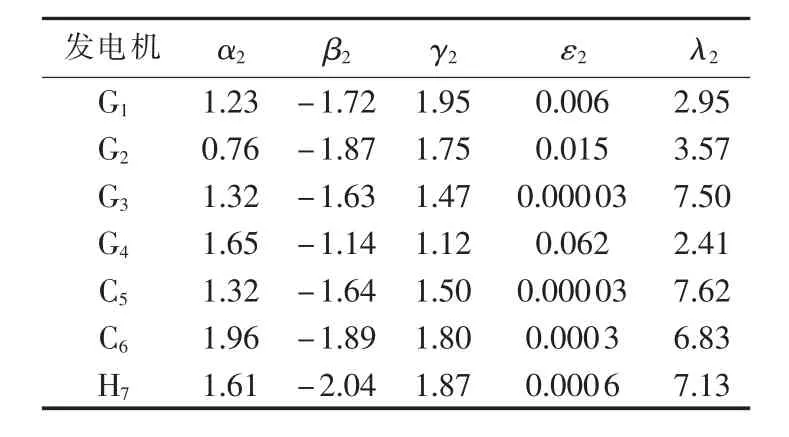
表3 各机组SO2排放参数Table 3 SO2emission parameters of units
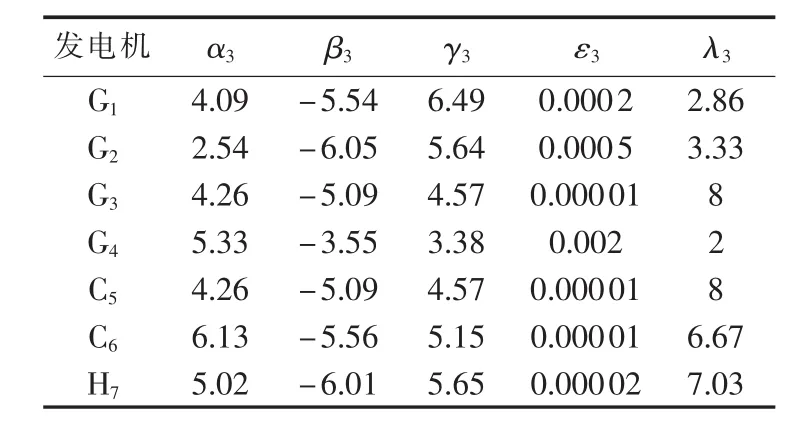
表4 各机组NOx排放参数Table 4 NOxemission parameters of units
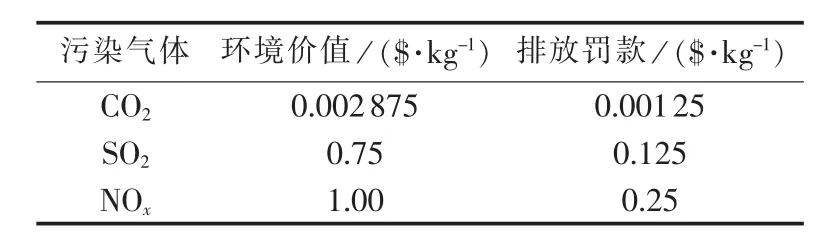
表5 电力行业污染气体排放标准Table 5 Pollutant emission specifications of electric power industry

表6 某地CCHP机组分时电价Table 6 TOU prices of a regional CCHP system

图3 3种算法的收敛特性对比Fig.3 Comparison of convergence among three algorithms
从表7中可以看出:PSO算法优化结果的随机性最大,SPSO算法优化结果的随机性次之,SC-PSO算法优化结果的随机性最小。这也说明了SC-PSO算法的寻优性能明显优于PSO算法,一定程度上比SPSO算法好。同时,从多次计算所得到的平均综合成本来看,融入耦合协调后的SC-PSO算法所求得平均综合成本最小,即更经济环保,其寻优所求的结果更加合理,进一步体现了该算法的优越性和有效性。
从图5所示机组出力分配的情况来看,在充分考虑峰谷分时电价对购售电成本的影响下,利用CCHP机组的能源集线器模型,在电、热(冷)负荷需求增加时,优先考虑增加CCHP机组的出力配额,从而降低系统的综合成本,使系统能够高效、节能、环保运行。
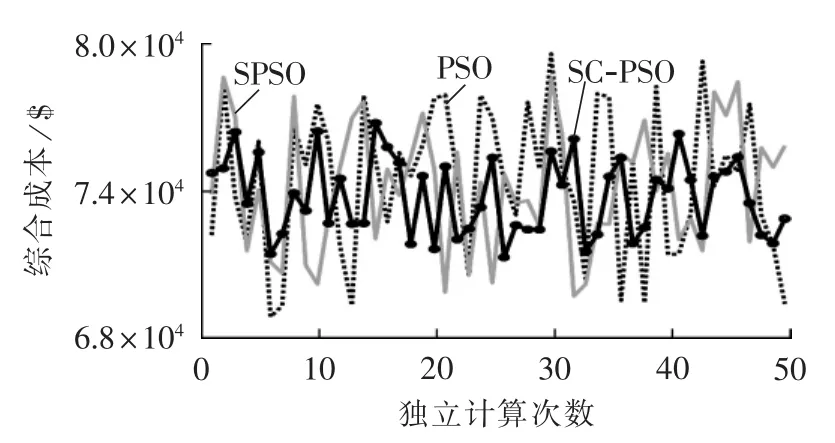
图4 3种算法50次独立计算结果分布Fig.4 Results of 50 independent calculations for three algorithms
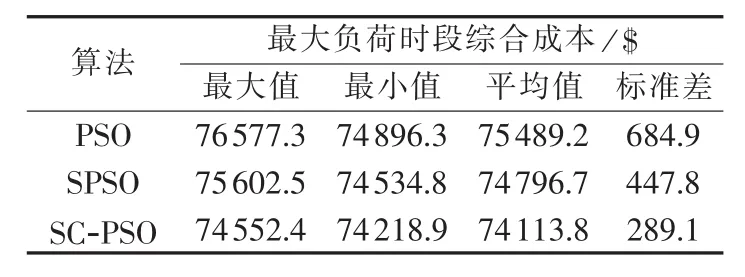
表7 3种算法50次独立计算的平均总成本Table 7 Statistics of 50 independent calculations for three algorithms
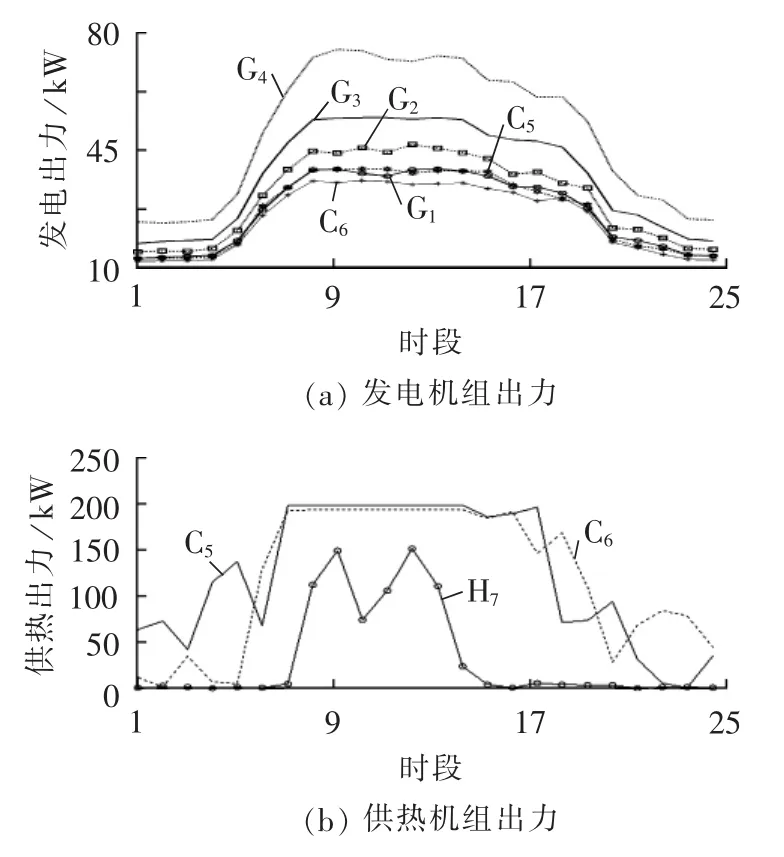
图5 机组出力优化结果Fig.5 Optimized outputs of different units
5 结论
充分考虑IES中电力、热力系统和天然气之间的交互影响,建立了CCHP系统区域联合环保经济调度模型,拓宽了IES中能量利用的相关性研究和计算思路。
在传统考虑燃料成本和排放污染气体所产生的环境成本的基础上,计及峰谷电价下的购售电成本不仅能够使CCHP参与需求侧管理,而且促使其获得更大的经济效益。
引入耦合协调数学模型而提出的SC-PSO算法,可针对性地解决PSO算法固有的随机性强、低效、容易陷入局部收敛而早熟的问题。仿真结果表明该方法不仅易于跳出早熟区间,增强全局寻优能力,而且提高了全局收敛性和效率,降低了随机性。
参考文献:
[1]贾宏杰,王丹,徐宪东,等.区域综合能源系统若干问题研究[J].电力系统自动化,2015,39(7):198-207.JIA Hongjie,WANG Dan,XU Xiandong,et al.Research on some key problems related to integrated energy systems[J].Automation of Electric Power Systems,2015,39(7):198-207.
[2]荆有印,白鹤,张建良.太阳能冷热电联供系统的多目标优化设计与运行策略分析[J].中国电机工程学报,2012,32(20):82-87,143.JING Youyin,BAI He,ZHANG Jianliang.Multi-objective optimization design and operation strategy analysis of a solar combined cooling heating and power system[J].Proceedings of the CSEE,2012,32(20):82-87,143.
[3]朱建文,石琳.天然气冷热电联产系统的应用与发展[J].华电技术,2014,36(10):73-76,80.ZHU Jianwen,SHI Lin.Application and development of natural gas CCHP production system[J].Huadian Technology,2014,36(10):73-76,80.
[4]冯志兵.燃气轮机冷热电联产系统集成理论与特性规律[D].北京:中国科学院工程热物理研究所,2006.FENG Zhibing.Integration principia and performance of CCHP with gas turbine[D].Beijing:Institute of Engineering Thermophysics,Chinese Academy of Sciences,2006.
[5]SAHIN C,SHAHIDEHPOUR M,ERKMEN I.Generationrisk assessment in volatile conditions with wind,hydro,and natural gas units[J].Applied Energy,2012,96(3):4-11.
[6]ALABDULWAHAB A,ABUSORRAH A,ZHANG X,et al.Coordination of interdependent natural gas and electricity infrastructures for firming the variability of wind energy in stochastic day-ahead scheduling[J].IEEE Transactions on Sustainable Energy,2015,6(2):606-615.
[7]徐宪东,贾宏杰,靳小龙,等.区域综合能源系统电/气/热混合潮流算法研究[J].中国电机工程学报,2015,35(14):3634-3642.XU Xiandong,JIA Hongjie ,JIN Xiaolong,et al.Study on hybrid heat-gas-power flow algorithm for integrated community energy system[J].Proceedings of the CSEE,2015,35(14):3634-3642.
[8]董军,张晓虎,李春雪,等.自动需求响应背景下考虑用户满意度的分时电价最优制定策略[J].电力自动化设备,2016,36(7):1-7.DONG Jun,ZHANG Xiaohu,LI Chunxue,etal.OptimalTOU pricing strategy considering user satisfaction in automated demand response background[J].Electric Power Automation Equipment,2016,36(7):1-7.
[9]崔强,王秀丽,王维洲.考虑风电消纳能力的高载能用户错峰峰谷电价研究[J].电网技术,2015,39(4):946-952.CUI Qiang,WANG Xiuli,WANG Weizhou.Stagger peak electricity price for heavy energy-consuming enterprises considering improvement of wind power accommodation[J].Power System Technology,2015,39(4):946-952.
[10]郭联哲,谭忠富,李晓军.基于用户响应下的分时电价优化设计模型与方法[J].电网技术,2006,30(5):24-28.GUO Lianzhe,TAN Zhongfu,LI Xiaojun.Demand response based model and method for optimal design of time-of-use electricity pirce[J].Power System Technology,2006,30(5):24-28.
[11]苏海锋,梁志瑞.基于峰谷电价的家用电动汽车居民小区有序充电控制方法[J].电力自动化设备,2015,35(6):17-22.SU Haifeng,LIANG Zhirui.Orderly charging control based on peak-valley electricity tariffs for household electric vehicles of residential quarter[J].Electric Power Automation Equipment,2015,35(6):17-22.
[12]PEHLIVANOGLU Y V.A new particle swarm optimization method enhanced with a periodic mutation strategy and neural networks[J].IEEE Transactions on Evolutionary Computation,2013,17(3):436-452.
[13]LI P,XU D,ZHOU Z Y,et al.Stochastic optimal operation of microgrid based on chaotic binary particle swarm optimization[J].IEEE Transactions on Smart Grid,2016,7(1):66-73.
[14]沈茂亚,丁晓群,王宽,等.自适应免疫粒子群算法在动态无功优化中应用[J].电力自动化设备,2007,27(1):31-35.SHEN Maoya,DING Xiaoqun,WANG Kun,et al.Application of adaptive immune PSO in dynamic reactive power optimization[J].Electric Power Automation Equipment,2007,27(1):31-35.
[15]邹恩,辛建涛,方仕勇,等.ICPSO算法及其在经济负荷分配中的应用[J].电力系统及其自动化学报,2012,24(4):19-24.ZOU En,XIN Jiantao,FANG Shiyong,et al.Improved chaotic particle swarm optimization algorithm and its application in economic load dispatch[J].Proceedings of the CSU-EPSA,2012,24(4):19-24.
[16]刘静,罗先觉.采用多目标随机黑洞粒子群优化算法的环境经济发电调度[J].中国电机工程学报,2010,30(34):105-111.LIU Jing,LUO Xianjue.Environmentaleconomicdispatching adopting multiobjective random black-hole particle swarm optimization algorithm[J].Proceedings of the CSEE,2010,30(34):105-111.
[17]周任军,李绍金,李红英,等.空间粒子群优化算法及其在电力系统环保经济负荷分配中的应用[J].电力自动化设备,2014,34(9):7-12.ZHOU Renjun,LI Shaoj in,LI Hongying,et al.Space particle swarm optimization algorithm and its application in environmental&economic load distribution of power system[J].Electric Power Automation Equipment,2014,34(9):7-12.
[18]杜晖.基于耦合关系的学术信息资源深度聚合研究[D].武汉:武汉大学,2013.DU Hui.Research on in-depth aggregation of academic information resource on the basis of coupling relationships[D].Wuhan:Wuhan University,2013.
