面向海量历史监测数据的谐波污染用户统计建模方法

邵振国，吴瑾樱，苏文博

（福州大学 电气工程与自动化学院，福建 福州 350116）

1 已有的谐波污染用户模型

由于大量电力电子装置及其他类型非线性负荷的不断增加，电网中的谐波污染日益严重，降低了电网运行可靠性［1］。建立谐波污染用户模型有助于分析用户污染域［2］，设计治理方案。

在稳定工作状态下，污染用户的谐波特性可统一表述成式（1）的形式［3］。

其中，Ih为用户发出的h次谐波电流；U1和U2、…、Uh分别为用户节点电压中的基波和各次谐波分量；C为用户控制参数。

式（1）考虑了不同次数谐波电压对用户谐波电流的影响，可称之为耦合模型。理论上只要给出电压波形和控制参数，通过供电电压和负荷的伏安特性就能够精确求解其注入系统的谐波电流值。但是在实际应用中往往不能得到式（1）的精确表达，并且也难以获得参数C，因而工程中常常对该模型进行不同程度的简化以得到一些实用化模型。文献［4］提出了配电网建模的诺顿等效法，将谐波源负荷表示成阻抗、电流源的组合模型，用一个恒定的阻抗模拟负荷的线性部分，用一个谐波电流源模拟负荷的非线性部分。文献［5］将不同次的谐波电压、电流之间的耦合关系线性化，提出了基于交叉频率导纳矩阵的谐波源模型。文献［6］将谐波源等效为恒流源和受控电流源，然后利用谐波监测数据进行模型参数辨识。

文献［7-8］利用时域状态估计技术对通用模型进行参数辨识。文献［9］利用模型中电压、电流之间的物理关系，通过对电流的最佳平方进行逼近辨识出模型参数，可对各种类型的负荷进行谐波建模。文献［10］利用现场测量数据来提高模型参数辨识的精度。这些参数辨识方法能够准确地得到通用模型的各个参数，但谐波幅值和相角的测量值是模型参数辨识必不可少的条件。由于判断谐波是否超标是以谐波幅值作为基准，同时为了节省存储空间，当前的电能质量监测数据往往只保存谐波幅值，而不保存相角，这就限制了以上参数辨识方法的应用。此外，谐波污染用户的工作状态具有随机性和时变性，模型参数不可能恒定不变。如果参数辨识样本集包含用户的多个工况数据，那么基于最佳估计思想的参数辨识结果并不能表征用户运行特性的变化。

本文提出一种基于谐波幅值监测数据的谐波用户建模思路，同时考虑用户模型参数的波动特点，建立谐波污染用户的统计模型。该方法采用用户的历史监测数据，不需要进行额外测量。计算结果为统计型模型参数，包含了用户工况的变化特征，因而能够更全面地评估用户运行污染。

2 基于谐波幅值监测数据的污染用户建模

2.1 用户污染模型

大电力用户由变压器和各种类型的用电设备构成，运行具有时变性和随机性，在高次谐波情况下还存在多种耦合作用，因此无法精确模拟。在谐波分析中，通常采用图1所示的负荷集总效应电路结构模拟污染用户。

图1 负荷谐波模型Fig.1 Model of load harmonic

图1 中，Us、Zs分别为系统电压和系统阻抗；Upcc、Ipcc分别为公共连接点（PCC）的电压、电流；R、X 分别表示用户负荷中电阻、电感元件部分的集总效应，一般电力用户负荷为感性负荷，因此模型中不含有电容元件；谐波电流源Ich表示非线性负荷产生的谐波交叉耦合效应。该模型将谐波污染用户负荷分为线性负荷部分和非线性负荷部分分别建模。在忽略系统背景谐波的情况下，可由图2所示的基波等效电路和谐波等效电路分别求解。 其中，Upcc1、Upcch分别为PCC的基波电压和谐波电压监测值，Ipcc1、Ipcch分别为PCC的基波电流和谐波电流监测值。

图2 谐波等效计算网络Fig.2 Equivalent calculation networks for harmonic analysis

2.2 线性负荷模型参数

将用户的线性负荷部分等效为并联阻抗，则其基波阻抗与谐波阻抗的关系如式（3）所示。

其中，Zch为线性负荷谐波等值阻抗；Zc1为线性负荷基波等值阻抗。

基波阻抗值可以由用户的基波电压、电流和功率因数测量值计算得到。

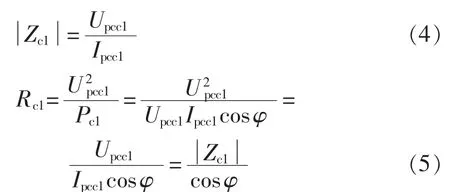
根据式（2）可以推导出基波电抗的计算公式，如式（6）所示。

2.3 非线性负荷模型参数

根据图2（b）所示电路，有如下关系式：

其中，Upcch、Ich分别为 Upcch、Ich的相量形式。

推导可得谐波电流源的幅值，如式（8）所示。

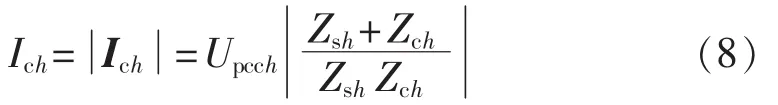
其中，Zsh为系统谐波等值阻抗，一般表示为串联阻抗。系统谐波阻抗与系统基波阻抗满足如式（19）所示关系。

许多相关文献已经研究了辨识系统谐波阻抗参数的方法，如文献［11］利用改进的偏最小二乘法求解系统阻抗，文献［12］应用秩次回归估计系统谐波阻抗。这些方法都能精确地估计出系统等效阻抗值。因此，本文在负荷谐波建模时假设系统阻抗已知。

由式（4）—（6）能够从谐波污染用户接入点的监测数据计算得到用户的线性负荷参数，由式（3）计算得到用户的非线性负荷参数，根据式（8）可计算得到谐波污染用户产生的谐波电流值。

3 基于拉丁超立方采样的统计建模

电力系统中的负荷类型复杂，运行方式也处在不断的变化之中，因而PCC的监测数据包含大量的随机波动成分，更适合采用统计型的模型参数描述用户的污染特性。

利用蒙特卡罗模拟（MC）法，对监测数据分组计算模型参数，进而进行概率统计分析，可得到统计型模型参数。根据GB／T19862—2005《电能质量监测设备通用要求》中的相关规定：谐波监测的一个基波记录周期为3s，存储记录周期为3min，即每3min产生一个保存记录。因此谐波污染用户接入点的监测数据有成千上万组，若对每组数据都进行计算，则存在计算量太大、占用内存太多的缺点，并不实用。为了缩短计算时间，提高计算效率，本文引入基于分层采样原理的拉丁超立方采样（LHS）方法处理海量历史监测数据，该方法可以在保证计算精度的前提下大幅减小采样数，提高计算效率。

3.1 拉丁超立方采样方法

拉丁超立方采样是M.D.Mckay等学者在1979年提出的一种分层采样方法［13］，具有采样效率高和稳健性好等优点。在进行相同规模的抽样时，该方法可以获得更高的精度。

拉丁超立方采样方法分为采样和排序2个步骤。采样时把随机变量累积分布函数的取值空间均分为N等份，从每个区间中随机选取一个数（或选择区间中间）作为累积分布函数的采样值，通过求反函数得到随机变量的采样值，形成采样矩阵S。

电力系统中输入随机变量的概率分布特性受众多因素影响，难以建立概率分布函数的准确模型。一般只能得到大量离散的监测数据。针对这种情况，本文利用离散拉丁超立方采样法处理用户接入点含有大量离散的历史监测数据而没有其准确的概率分布函数的情形。

根据大数定律，随机事件发生的频率依概率收敛于该事件发生的概率。因此，离散拉丁超立方采样并不计算具体的样本值，而是计算在一定的样本容量下某一状态的数据。对于采样规模N，输入随机变量X处于状态xi的个数与其处于该状态的概率成正比，即：

其中，xi为随机变量X的第i个样本值；n（xi）为随机变量X处于状态xi的个数；P（xi）为随机变量X处于状态xi的概率。

采样过程具体实现如下。

将单个随机变量的离散数据按从小到大的顺序排序，并分成N等份，则每个子区间中包含n／N个样本。 第 j个子区间（（j-1） ／N，j／N］的元素在数组中的分布范围可由式（11）确定。由拉丁超立方采样法的原理可知，第j个子区间对应的样本可取区间内任意的值，根据式（12）确定。

其中，a为子区间元素范围下限；b为子区间元素范围上限；k为第j个子区间采样值在排序后的数字的位置；round为小数部分四舍五入取整函数；rand为随机数生成函数。

所有随机变量都完成采样后，对采样样本进行排序，降低采样值之间相关性对拉丁超立方采样模拟精度的影响［14］。排序方法有多种，如Gram-Schmidt序列正交化方法［15］、Cholesky 分解法［16］等。 对于具有相关性的随机变量，亦可通过排序方法［17-18］使得随机变量采样值间的相关性尽可能接近随机变量间的相关性。对于离散的历史监测数据，各个变量之间的相关性可用其相关系数矩阵表示，结合Cholesky分解法进行排序能够很方便地处理变量之间的相关性。

3.2 统计建模步骤

利用拉丁超立方采样法进行谐波污染用户统计建模的步骤如下：

a.输入PCC的历史监测数据，包括电压、电流幅值和功率因数；

b.利用上述单个随机变量的采样方法对离散数据中的各个变量进行采样，得到初始样本矩阵；

c.利用Cholesky分解法，根据相关系数矩阵对初始样本矩阵进行排序，形成计算样本；

d.对每一组样本数据按式（4）—（6）和式（8）计算模型参数，并保存计算结果；

e.按步骤a—d完成对所有样本数据的计算后，通过统计学方法求得负荷谐波模型中电阻、电抗、阻抗和谐波电流的期望值与方差等数字特征及其概率分布曲线。

4 仿真算例

为了验证本文所提方法的正确性，通过仿真模拟了污染用户的运行工况，此后采用MATLAB进行建模。仿真中系统侧基波阻抗参数为：Rs1=0.03 Ω、Xs1=0.1 Ω；用户侧基波阻抗参数为：Rc1=5 Ω、Xc1=15 Ω，用户5次谐波注入电流均值为14.14 A。假设谐波用户负荷参数服从正态分布，其标准差为均值的10%。利用MATLAB的随机数生成器得到负荷节点的运行样本数据作为监测数据。

利用拉丁超立方抽样法对监测数据进行抽样，得到基波电压、电流，谐波电压、电流和功率因数的采样数据，本文采样次数取500次。对500组采样数据分别进行确定性的负荷模型参数计算，得到500组结果，进行概率统计分析后可得到模型参数的期望值、方差和累积分布曲线等。将计算结果与实际的仿真参数进行对比，结果列在表1中。模型参数的概率分布曲线分别如图3所示。根据图中结果和表中数据对比可以看出，采用拉丁超立方抽样的计算结果能够准确地估计模型的统计特征参数，在大幅减小计算量的情况下，精度较高。

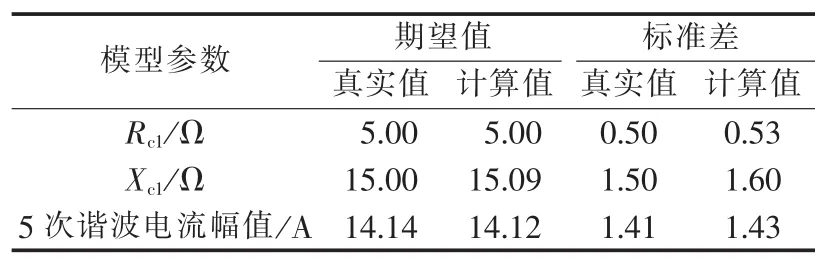
表1 模型参数计算值与真实值的对比Table1 Comparison between calculated and actual model parameters

图3 模型参数的概率分布曲线Fig.3 Probability distribution curve for different model parameters

5 工程算例

实测数据来源于某变电站10 kV出线，每3min记录一次，记录数据为基波和各次谐波电压、电流幅值，同时可以获取运行时的功率因数。此处采用的是基波电压、电流幅值与5次谐波电压、电流幅值进行参数辨识。15d的6900组监测数据波形如图4所示，波形从上至下分别为基波电压、电流幅值与5次谐波电压、电流幅值。

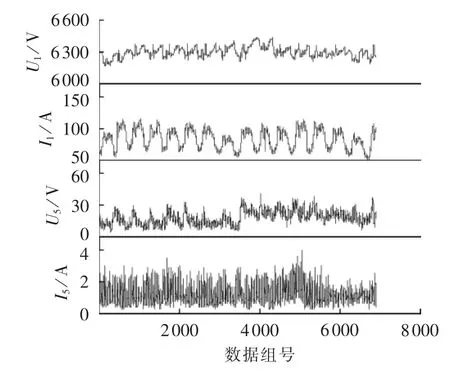
图4 电压、电流幅值监测数据Fig.4 Monitored measurements of voltage and current

分别采用蒙特卡罗模拟法和拉丁超立方采样法进行参数辨识。其中，蒙特卡罗模拟法需要对每一组监测数据进行一次计算，即需要6900次计算，而拉丁超立方采样法在500次抽样时就能达到较好的计算精度。对比可以看出，拉丁超立方采样法降低计算量的效果十分明显，而该方法所增加的只是对大量离散监测数据的采样过程，该过程额外增加的时间相比于节省的计算时间要少得多。由此可知，拉丁超立方采样法具有减小蒙特卡罗法计算量的作用，并且监测数据的规模越大，其效果越明显。

蒙特卡罗模拟法和拉丁超立方采样法进行统计建模的计算结果的期望值和标准差列在表2中，其概率分布曲线如图5所示。

通过仿真对比可以看出，本文方法能从大量的历史监测数据中准确得到用户模型参数的统计特征参数，从而快速地建立用户的谐波污染统计模型，具有较好的工程应用价值。

表2 2种方法的计算结果Table 2 Calculated results by two methods

图5 2种方法得到的模型参数的概率分布曲线对比Fig.5 Comparison of model parameter probability distribution between two methods

6 结论

针对电网中部分历史监测数据只保留用户电压、电流谐波幅值，而缺少谐波相角的情形，本文提出了一种基于谐波幅值的建模方法。该方法根据电压、电流基波和谐波幅值以及功率因数计算负荷谐波模型参数，对实际工程较为实用。同时考虑用户运行中具有的随机波动特性，利用拉丁超立方采样法由大量的历史监测数据计算模型参数的数字特征及其概率分布曲线。与传统蒙特卡罗模拟法相比，计算量小且精度高，可用于实际的谐波污染用户统计建模分析，具有很高的工程应用价值。仿真算例和工程实例证明了所提方法的有效性、准确性和快速性。

［1］林海雪.电力网中的谐波［M］.北京：中国电力出版社，1998：56-78.

［2］CHANG G，HATZIADONIU C，XU W，et al.Modeling devices with nonlinear voltage-current characteristics for harmonic studies［J］.IEEE Transactions on Power Delivery，2004，19 （4）：1802-1811.

［3］Task Force on Harmonics Simulation.Modeling and simulation of the propagation of harmonics in electric power networks，part I：concepts，models，and simulation techniques［J］.IEEE Transactions on Power Delivery，1996，11（1）：452-465.

［4］THUNBERG E，SODER L.A Norton approach to distribution network modeling for harmonic studies［J］.IEEE Transactions on Power Delivery，1999，14（1）：272-277.

［5］FAURI M.Harmonic modelling of non-linear load by means of crossed frequency admittance matrix［J］.IEEE Transactions on Power Systems，1997，12（4）：1632-1638.

［6］赵勇，张涛，李建华，等.一种新的谐波源简化模型［J］.中国电机工程学报，2002，22（4）：46-51.ZHAO Yong，ZHANG Tao，LI Jianhua，et al.A new simplified harmonic source model for harmonic analysis and mitigation ［J］.Proceedings of the CSEE，2002，22（4）：46-51.

［7］吴笃贵，徐政. 电力负荷的谐波建模［J］. 电网技术，2004，28（3）：20-24.WU Dugui，XU Zheng.Harmonic modeling of electric loads［J］.Power System Technology，2004，28（3）：20-24.

［8］SOLIMAN S A，AL-KANDARI A M，EL-HAWARY M E.Time domain estimation techniques for harmonic load models［J］.Electric Machines and Power Systems，1997，25（8）：885-896.

［9］冯士刚，艾芊.一种谐波负荷建模的新方法［J］.电力系统自动化，2007，31（17）：26-30.FENG Shigang，AI Qian.A new approach for harmonic modeling ofelectricloads［J］.Automation ofElectric PowerSystems，2007，31（17）：26-30.

［10］RUDION K，GUO H，ABILDGAARD H，et al.Non-linear load modeling-requirements and preparation for measurement［C］∥2009 IEEE Power&Energy Society General Meeting.Calgary，AB，Canada：IEEE，2009：1-7.

［11］李丽，马宏忠，姜宁，等.基于改进偏最小二乘法的系统谐波阻抗及谐波发射水平估算［J］.电力系统保护与控制，2011，39（1）：92-95.LI Li，MA Hongzhong，JIANG Ning，et al.Assessing harmonic impedance and the harmonic emission level based on improved partial least-squares regression method［J］.Power System Protection and Control，2011，39（1）：92-95.

［12］解绍锋.基于秩次回归的系统谐波阻抗分析与谐波评估方法［J］. 电力自动化设备，2010，30（11）：29-33.XIE Shaofeng.Harmonic impedance analysisand harmonic assessment based on rank regression［J］.Electric Power Automation Equipment，2010，30（11）：29-33.

［13］MCKAY M D.A comparison of three methods for selecting values of input variables in the analysis of output from a computer code［J］.Technometrics，2000，42（1）：55-61.

［14］蔡德福，石东源，陈金富.基于多项式正态变换和拉丁超立方采样的概率潮流计算方法［J］. 中国电机工程学报，2013，33（13）：92-100.CAI Defu，SHI Dongyuan，CHEN Jinfu.Probabilistic load flow calculation method based on polynomial normal transformation and Latin hypercube sampling［J］.Proceedings of the CSEE，2013，33（13）：92-100.

［15］于晗，钟志勇，黄杰波，等.采用拉丁超立方采样的电力系统概率潮流计算方法［J］. 电力系统自动化，2009，33（21）：32-35.YU Han，CHUANG Chiyong，WONG Kitpo，et al.A probabilistic load flow calculation method with Latin hypercube sampling［J］.Automation of Electric Power Systems，2009，33（21）：32-35.

［16］YU Han，CHUANG Chiyong，WONG Kitpo.Probabilistic load flow evaluation with hybrid Latin hypercube sampling and Cholesky decomposition［J］.IEEE Transactions on Power Systems，2009，24（2）：661-667.

［17］陈雁，文劲宇，程时杰.考虑输入变量相关性的概率潮流计算方法［J］. 中国电机工程学报，2011，31（22）：80-87.CHEN Yan，WEN Jinyu，CHENG Shijie.Probabilistic load flow analysis considering dependencies among input random variables［J］.Proceedings of the CSEE，2011，31（22）：80-87.

［18］徐潇源，严正，冯冬涵，等.基于输入变量秩相关系数的概率潮流计算方法［J］. 电力系统自动化，2014，38（12）：54-61.XU Xiaoyuan，YAN Zheng，FENG Donghan，et al.Probabilistic load flow calculation based on rank correlation coefficient of input random variables［J］.Automation of Electric Power Systems，2014，38（12）：54-61.