基于混合光线反射优化算法的最近电压稳定临界点求取方法

方斯顿 ，程浩忠 ，徐国栋 ，曾平良 ，姚良忠

（1.上海交通大学 电力传输与功率变换控制教育部重点实验室，上海 200240；2.中国电力科学研究院，北京 100192）

0 引言

电力系统电压稳定性与系统最大传输容量密切相关。因此，电压稳定性评估是电压安全分析的研究重点之一［1］。当节点负荷增长方式固定时，通常可采用连续潮流法［2］、崩溃点法［3］和非线性规划法［4-5］进行求解。但电力系统在实际运行中存在大量不确定因素［6］，这给节点注入功率带来不确定性。以风电、光伏为代表的可再生能源具有较高的功率因数，其大规模接入电网使得负荷增长不确定性也急剧增加［7］。因此，如何在考虑负荷增长方向不确定性的情况下求取最近电压稳定临界点是保障系统安全稳定运行的重要手段。

最近电压稳定临界点问题首先由Dobson在文献［8］中提出。Dobson指出，最近电压稳定临界点的求解目标是找出距当前运行点“最近”的电压稳定临界点，并提出利用极限曲面法向量修正负荷增长方向，从而通过迭代求得最近电压稳定临界点的方法。但该方法存在2点不足：第一，该方法未限定负荷增长方向不确定性的范围，求出的电压稳定裕度甚至可能小于基态值，这在实际运行中出现的可能性极小；第二，由于极限曲面性质复杂，当系统增大时算法容易陷入局部最优，造成评价结果不准确。

根据鲁棒优化理论，求取最近电压稳定点可转化为内层嵌套连续潮流计算的双层规划模型［9］。求解该问题可分为2种途径。第一类方法首先利用近似曲面逼近极限曲面，然后将原问题转化为“预估-校正”模式。如文献［9］采用超平面逼近电压稳定极限曲面，通过该平面预估最危险负荷增长方向并采用连续潮流进行校正。这类方法效率较高，算法鲁棒性好，收敛可靠，但受限于曲面逼近的精度，这类方法全局寻优能力不强。另一类方法是采用智能算法，如 Big Bang-Big Crunch 算法［10-11］、支持向量机［12］等。这类方法不受极限曲面复杂性影响，具有较强全局寻优能力，但计算效率偏低。光线反射优化OIO（Optics Inspired Optimization）算法由 Kashan于2014年提出［13］，该算法将待优化函数曲面根据局部凹凸性质分别看成凹面镜和凸面镜，将可行解看作光源，利用光源发出光线在凹面镜和凸面镜上汇聚、发散成像（产生新的可行解）。由于其利用待优化函数曲线的局部凹凸性质，适合于约束少而待优化函数性质复杂的优化问题，近百个标准测试函数的仿真证明其具有较高的计算效率及很强的寻优能力，明显优于粒子群优化PSO（Particle Swarm Optimization）算法［14］、遗传算法 GA（Genetic Algorithm）［15］等目前常用的智能算法。

为进一步增强该算法的全局寻优能力，本文基于House-Holder变换和混合多光源策略提出混合光线反射优化SOIO（Shuffled OIO）算法，并首次将该方法应用于最近电压稳定临界点求取中。算例分析表明本文方法可有效求解该问题，计算效率高且全局搜索能力强。

1 最近电压稳定临界点模型

1.1 参数化潮流方程

含负荷参数的潮流方程可表示为［16］：

其中，x∈Rn为节点电压列向量；λ∈R为负荷参数，本文不考虑发电机的出力增长方式变化；P（λ）∈Rn和Q（λ）∈Rn为此时的节点注入功率列向量；f：Rn×R2nR2n为含参数潮流方程。

定义 λv=（PT（λ），QT（λ））T，随着负荷参数 λ 逐渐增长，电力系统会达到某个电压稳定临界点（PT（λc），QT（λc））T。 由所有临界点组成的电压稳定极限曲面可定义为：

其中，f（·）=0为电压稳定临界点处的系统潮流方程，表达式详见式（1）；ΩSNB、ΩLIB分别为 SNB 型和LIB型电压稳定临界点；∑∈R2n-1为系统所有可能的电压稳定临界点处节点注入功率构成的超曲面。

在图1中，∑代表极限曲面，包括SNB和LIB型的电压失稳点。代表基态运行点；d0为预测负荷增长方向；E1+ξ和E1-ξ分别代表负荷增长方向的上、下限，其中ξ∈R2n，E1表示元素全为1的向量。

图1 电压稳定极限曲面Fig.1 Voltage-stability limit surface

1.2 最近电压稳定临界点两层规划模型

最近电压稳定临界点是所有可能的电压稳定临界点中离基态运行点最近的点。根据鲁棒优化理论，该问题求取可表示为两层优化模型［9］。下层问题是求取某一可能负荷增长方向上的电压稳定临界点，通常采用连续潮流法［2］求解；上层问题则是求取在负荷增长方向约束的条件下最危险的负荷增长方向。

两层模型详细描述如下。

上层：

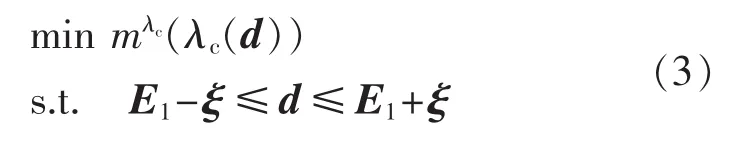
其中，d 为某负荷增长方向；λc（d）=λcd.× λ0（d），“.× ”表示逐位相乘；mλc（λc（d））=|λc（d）-λ0（d）|。

下层：

不等式约束包括发电机有功出力上、下限约束。两层模型关系如图2所示。

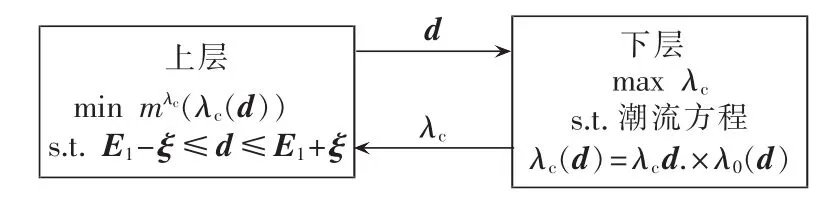
图2 两层模型关系Fig.2 Relationship between two levels of model

2 光线反射优化算法

光线反射算法由Kashan于2014年提出［13］，其直接利用待优化函数的局部几何特性，计算效率高且具有较强全局寻优能力，其过程简述如下。

2.1 光线反射定律

光线在凹面镜和凸面镜上反射时成像情况分别如图3（a）、（b）所示。

图3 球面镜成像原理Fig.3 Principle of spherical mirror imaging

图3中，r和fo分别为球面镜曲率和焦距，满足r=2fo。如图所示，凹面镜对光线有汇聚作用，根据物体距凹面镜的距离不同分别成放大、缩小的实像（实线）及放大、缩小的虚像（虚线），如图3（a）所示；而凸面镜对光线具有发散效果，成像为缩小的虚像（虚线），如图3（b）所示。

为方便进一步分析，定义光源长度为lHO，所成像长度为lHI，光源离球面镜距离为p，像距离球面镜q，球面镜焦距fo，球面镜曲率r。本文中，在球面镜以上距离为正，在球面镜以下距离为负。以凹面镜为例，各量如图4所示，各量之间满足球面镜反射公式［17］，如下式所示：

此外，根据相似三角形可得：

图4 球面镜反射参量定义Fig.4 Definition of spherical mirror reflection parameters

2.2 可行解产生机制

基于前文叙述，函数曲面为凹时光线反射算法的可行解产生机制如图5所示。

图5 可行解产生示意图Fig.5 Schematic diagram of feasible solution generation

图中 g（Y）=g（y1，y2，…，yn）为待优化函数，其中lmin≤yi≤lmax（i=1，2，…，n），g：RnR。 优化问题的目标是在可行域内寻找g的全局最优解Y*∈Rn，使得 g（Y*）≤g（Y）（∀Y∈Rn）。 图中各变量定义如下：代表第j个光源在Rn空间里的投影，即原问题第j个可行解；代表寻优空间中的另一个点，ik是该点在光源群中的标号，ik∈｛1，2，…，lNO｝，定义水平线通过点代表像点在Rn空间里的投影，由光源点通过确定的轴线反射而成为光源点距离的距离；为水平线与光源点之间距离；为水平线与像点之间距离；为水平线到曲率中心距离；为曲率中心到的距离；为光源长度；为像长度。上标t均代表第t次迭代。

基于以上定义，设种群中共有lNO个光源投影，对第j个光源投影，在种群中选择任意，若，则设函数曲面为凹面镜，反之为凸面镜；不失一般性，下文叙述过程中函数曲面均设为凹面镜。函数曲面为凸时过程类似，详见文献［13］。

在均匀分布中随机产生和，C为某设定常数；则入射光源点坐标和曲率中心分别可表示为如式（7）所示。

由此可得，，根据式（5）可得：

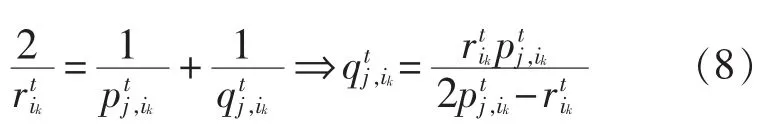
又可得：

由式（6）得：

由此可得：

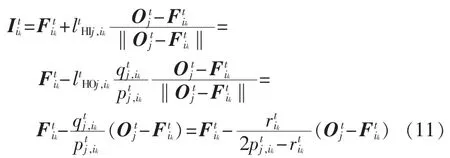
根据以上方法，可由解在解空间中产生另一可行解

3 混合光线反射优化算法

光线反射优化算法直接利用待优化函数的局部几何性质，可有效产生更优秀的个体。本文在原始光线反射优化算法的基础上提出基于House-Holder变换的变异策略和混合多光源策略，进一步改善算法性能。

3.1 基于House-Holder变换的可行解变异策略

文献［13］提出旋转光线反射优化ROIO（Rotation OIO）算法，但将所有解全部进行House-Holder旋转变换会破坏原有可行解的结构，因此本文采用该旋转变换以一定概率对所得解进行变异。该方法是以一定概率对生成解进行旋转变换获得如式（12）所示。

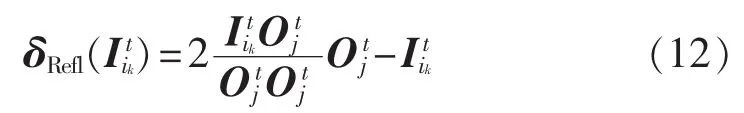
3.2 混合光线反射优化算法流程

单一种群下智能算法容易早熟，不利于提高算法全局收敛性，因此本文提出采用混合多光源策略，进一步提高算法的全局收敛能力，所得混合光线反射优化算法流程如下。

步骤1：初始参数设定。光源总群体数lNO，光源子群体数m，局部搜索次数上限N1，全局搜索次数Ng。

步骤2：在负荷增长方向范围内随机产生lNO个光源，第j个光源设为全局迭代计数器t=1。

步骤3：t=t+1，以每个光源向量为负荷增长方向，并进行连续潮流计算，获得各光源的电压稳定裕度

步骤4：将所有光源按升序排列，记电压稳定裕度最小的为，将全体光源按电压稳定裕度划分为m个子群，其中，第1个光源放入种群1，第m个放入种群m，第m+1个放入种群1，依此类推。

步骤5：在每个子光源群中，根据各光源所对应电压稳定裕度，记最差的光源（电压稳定裕度最小），最好为（电压稳定裕度最大），对利用2.2节中方法与产生像，若，则替换；若无改变，则替换，继续更新；重复这一过程直到被替换或达到局部搜索次数上限N1。

步骤6：对每个子光源群中，除去最优光源外，利用选择机制选择一个光源进行变异，对其利用3.1节中方法产生变异解

步骤7：混合光源群，重复步骤4—6，直到全局迭代次数Ng；获得光源对应负荷增长方向为最危险增长方向，与之对应的电压稳定裕度为最近电压稳定临界点。

4 算例分析

4.1 最近电压稳定临界点

4.1.1 算例设置

以多个IEEE标准系统作为测试算例［18］，负荷和发电机出力均按初始基准比例增长。负荷增长方向不确定量ξ中各元素ξi均相等，光源总数lNO设为30，子光源群数目m=6；局部迭代次数N1和全局迭代次数 Ng分别为 10 和35，参数此外，为衡量负荷增长不确定性对静态电压稳定裕度的影响，定义电压稳定裕度减少量：

其中，ME为固定负荷增长方向时的静态电压稳定裕度；Mξ为考虑负荷增长不确定性时的静态电压稳定裕度。

4.1.2 优化效果分析

用 IEEE 30、57、118、300、2736sp、2746wp 系统作为测试。本文方法所得静态电压稳定裕度Mξ和Er结果如表1所示。

表1 本文方法最近电压稳定临界点计算结果Table 1 Calculated closest critical points by proposed algorithm

从以上数据可知，采用本文所提算法可有效计算最危险负荷增长方向，所得结论如下：

a.负荷增长方向的不确定性会加大系统运行风险，会显著降低运行点的电压稳定裕度；

b.在含不确定新能源的电网的安全分析中，仅对固定负荷增长方向进行分析远远不够，应当计及负荷增长的不确定性对电压稳定裕度进行校核。

4.2 算法效率分析

4.2.1 计算耗时分析

本文采用计算仿真平台Intel Core Dual i7-3820（3.6 GHz，RAM 8 GB，MATLAB2013a）。 以 IEEE 118节点系统为例，分别采用本文方法、遗传算法和粒子群优化算法计算100次，平均收敛性曲线如图6所示。所求得的电压稳定裕度λ、收敛平均迭代次数N、平均计算耗时t如表2所示。遗传算法参数：种群数30，交叉率0.8，变异率0.2，自然数编码。粒子群优化算法参数：粒子数30，惯性权重0.8，局部与全局学习因子2，自然数编码。

图6 3种方法所得的收敛曲线Fig.6 Convergence curve for three algorithms

表2 3种算法所得的计算效率Table 2 Computational efficiency for three algorithms

从图6和表2中数据可得，本文算法效率高于其他2种算法，可兼顾计算效率与准确性，从而准确评估最近电压稳定点处的稳定裕度。

4.2.2 参数对SOIO算法寻优效果影响

为分析本文算法参数设置对算法效率的影响，以IEEE 118节点系统为例，光源总数lNO和光源子群数目m与对应最危险电压稳定裕度关系如图7所示。

图7 参数对寻优效果影响Fig.7 Influence of parameters on searching effect

从图中可得，当lNO和m都增大时，算法的寻优效率提高。当lNO增加时，种群光源多，使得全局寻优能力变强；而当m增加时，局部搜索效率提升，算法更容易发掘最优解，也会提高算法寻优效率。但从曲面对各坐标轴投影的斜率也可以看出，子群数目对算法效率影响更大。进一步地，当lNO和m均大于一定数值时算法寻优能力与参数关系不大，这证明了本文算法参数选择的鲁棒性。

4.2.3 改进策略对算法效率影响

为评价本文改进策略的有效性，通过采用或不采用改进策略对算法效率进行比较，2种策略均采用的算法为混合光线反射优化算法，结果见表2；不采用变异策略但保留混合策略的为SOIO2，采用变异策略不采用混合策略的为OIO1，2种策略均不采用的为OIO2，3种算法计算结果如表3所示。

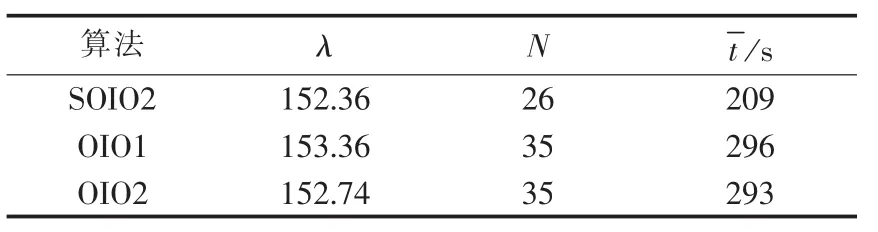
表3 3种算法计算效率对比Table 3 Comparison of computational efficiency among three algorithms

从表中数据可知本文所采用的改进策略的有效性。算法效率SOIO＞SOIO2＞OIO1＞OIO2，这是由于采取变异策略时可增加光源的多样性，从而增强了算法接受劣解的能力，因此全局寻优能力增强，算法效率高；而混合多光源策略的采用则增强了局部搜索能力。而从效率顺序也可得，混合策略对算法效率的提高作用强于变异策略。

5 结论

针对目前算法求解最近电压稳定临界点时在计算精度和效率上的矛盾，本文提出混合光线反射优化算法对该问题进行求解，得到结论如下。

a.当考虑负荷增长方式不确定性时，最近电压稳定临界点的电压稳定裕度会有明显下降，会给系统带来运行风险；因此，在含大量新能源的电网中，应当对最近电压稳定裕度进行校核。

b.本文提出的混合光线反射优化算法可有效求解最近电压稳定临界点问题，与粒子群优化算法和遗传算法的对比证明其具有更好的收敛特性。

c.对算法参数的分析表明，子群体数目和种群规模均对算法寻优效率影响较大，且子群规模作用强于种群规模，当参数大于一定数值后，算法对参数选择具有一定鲁棒性，参数变化对算法性能影响不大。

d.对改进策略的研究表明，本文提出的2种改进策略均可有效提高算法效率，且其中混合多光源策略的作用强于变异策略。

［1］MANANDUR K R C，CHENOWETH R D.Optimal control of reactive power flow for improvements in voltage profiles and real power loss minimization［J］.IEEE Trans on Power Apparatus and Systems，1981，100（7）：3185-3194.

［2］AJJARAPU V，CHRISTY C.The continuation power flow：a tool for steady state voltage stability analysis［J］.IEEE Trans on Power Systems，1992，7（1）：416-423.

［3］CANIZARES C A，ALVARADO F L.Point of collapse and continuation methods for large AC-DC systems［J］.IEEE Trans on Power Systems，1993，8（1）：1-8.

［4］IRISARRI G D，WANG X，TONG J，et al.Maximum loadability ofpowersystemsusing interiorpointnonlinearoptimization method［J］.IEEE Trans on Power Systems，1997，12（1）：162-172.

［5］韦化，丁晓莺.基于现代内点理论的电压稳定临界点算法［J］.中国电机工程学报，2002，22（3）：27-31.WEI Hua，DING Xiaoying.An algorithm for determining voltage stability critical point based on interior point theory［J］.Proceedings of the CSEE，2002，22（3）：27-31.

［6］HU Zechun，WANG Xifan.A probabilisticload flow method considering branch outages［J］.IEEE Trans on Power Systems，2006，21（2）：507-514.

［7］HU Zechun，WANG Xifan，TAYLOR G.Stochastic optimal reactive power dispatch：formulation and solution method［J］.International Journal of Electrical Power and Energy Systems，2010，32：615-621.

［8］DOBSON I，LU L.New methods for computing a closest saddle node bifurcation and worst case load power margin for voltage collapse［J］.IEEE Trans on Power Systems，1993，8（3）：905-913.

［9］胡泽春，王锡凡，程浩忠.最近电压稳定临界点的两层规划模型和信赖域算法［J］.中国电机工程学报，2008，28（1）：6-12.HU Zechun，WANG Xifan，CHENG Haozhong. A bilevel programming formulation and trust region approach for closet critical point of voltage stability［J］.Proceedings of the CSEE，2008，28（1）：6-12.

［10］EROL O K，EKSIN I.A new optimization method：Big Bang-Big Crunch［J］.Advances in Engineering Software，2006，37（2）：106-111.

［11］DJILANI B.Big Bang-Big Crunch optimization algorithm for the maximum power point tracking in photovoltaic system［J］.IJMER，2014，4（9）：11-17.

［12］SUGANYADEVI V M，BABULAL K C，KALYANI S，et al.Assessmentofvoltage stability margin by comparing various support vector regression models［J］.Soft Computing，2014，12：54-61.

［13］KASHAN A H.A new meta-heuristic for optimization：optics inspired optimization［J］.Computer&Operations Research，2015，55：99-125.

［14］冯士刚，艾芊.带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用［J］.电工技术学报，2007，22（12）：145-151.FENG Shigang，AI Qian.Application of fast and elitist nondominated sorting generic algorithm in multi-objective reactive power optimization［J］.Transactions of China Electrotechnical Society，2007，22（12）：145-151.

［15］张聪誉，陈民铀，罗辞勇，等.基于多目标粒子群算法的电力系统无功优化［J］.电力系统保护与控制，2010，38（20）：153-159.ZHANG Congyu，CHEN Minyou，LUO Ciyong，et al.Power system reactive power optimization based on multi-objective particle swarm algorithm［J］.Power System Protection and Control，2010，38（20）：153-159.

（continued on page 75）（continued from page 62）

［16］KATAOKA Y，SHINODA Y.Voltage stability limit of electric power systems with generator reactive power constraints considered［J］.IEEE Trans on Power Systems，2005，20（2）：951-963.

［17］ZITZEWITZ P W，ELLIOTT T G，HAASE D G，et al.Physics：principles and problems［M］.Glencoe，USA：McGraw-Hill，2005.

［18］Power Systems Engineering Research Center（PSERC）.MATPOWER4.1［EB／OL］. ［2015-03-01］.http：∥www.pserc.cornell.edu／matpower／.