基于导纳重构的大型光伏电站谐波谐振抑制策略

郑 晨，周 林，张 密

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.国网重庆市电力公司长寿供电分公司，重庆 401220）

0 引言

相比分布式光伏发电系统，大型光伏电站以其独有的高效率、集中管理等优势已成为光伏发电产业的重要趋势［1-5］。由于电网阻抗的存在，大型光伏电站与电网之间以及光伏电站内各逆变器之间的相互影响日益凸显［3-5］。

已有部分文献对电网阻抗引起的并网逆变器稳定性问题进行研究，可归为2类：一类是从电流环传递函数角度分析［5-8］，另一类是从系统阻抗角度分析［9-11］。 文献［9］根据直流系统的稳定性判据，拓展得到交流系统源与载的阻抗稳定性判据；文献［10］在广义奈奎斯特稳定性判据基础上，简化得到关于d轴输出导纳的稳定性判据；文献［11］以小功率并联整流器为背景，将阻抗稳定性判据扩展到2台整流器并联系统。然而这些方法都是针对单个逆变器或微电网系统，不能直接用来判别大型光伏电站的稳定性。文献［5］提出利用大型光伏电站电流闭环传递函数的根轨迹来分析电网阻抗对系统稳定性的影响；文献［6-8］利用电流开环传递函数的伯德图来研究电网阻抗对系统稳定性的影响。但此类方法需要知道大型光伏电站的精确数学模型。

针对电网阻抗引起的并网逆变器谐波谐振问题，已有部分文献提出了解决方案，文献［11］采用阻性功率因数校正装置抑制系统的谐波谐振，但该方法提高了成本，降低了系统可靠性；文献［12-13］通过检测谐振频率、电网阻抗等，在线调整控制器参数，但该类方法需要复杂的检测与控制算法；文献［14］通过反馈并网点电压的高阶微分环节来提高系统对电网阻抗变化的适应能力，但高阶微分环节在工程中难以实现，容易引入噪声干扰；文献［15］在滤波电感L1和电容C支路串联或者并联虚拟电阻来改善逆变器的输出阻抗，但该方法在改变输出阻抗的同时也改变了电流环的控制性能；文献［16］对逆变器输出阻抗特定频率处的相位进行补偿，进而提高系统的稳定性，但该方法需要实时检测电网阻抗来确定需要补偿的频率点。因此难以将上述方法借鉴到大型光伏电站中。

基于上述分析，本文首先根据大型光伏电站诺顿等效模型，推导出一种基于系统导纳的大型光伏电站稳定性判据；然后提出一种对系统输出导纳相位和幅值进行改善的导纳重构策略，该策略能够提高光伏电站的稳定性，实现对谐波谐振的抑制；最后通过仿真及实验对本文理论分析进行验证。

1 基于系统导纳的大型光伏电站稳定性判据

1.1 大型光伏电站等效模型

大型光伏电站通常由多台LCL型并网逆变器并联组成，其等效电路结构如图1 所示［2，4-5］。 其中，L1j、Cfj、L2j分别为逆变器j的逆变器侧电感、滤波电容及网侧电感；isjabc为逆变器j的并网电流；upabc、ugabc分别为三相并网点电压和理想电网电压；Zg为等效电网阻抗，主要包括升压变压器漏感抗和长距离高压输电线路的等效电阻、电抗，由于高压输电线路的电阻远小于电抗，因此本文只考虑感性分量，记 Zg（s）=sLg，对应的导纳 Yg（s）=1 ／Zg（s）。

图1 大型光伏电站拓扑结构Fig.1 Topology of LSPV

工程实际中，光伏电站中的所有逆变器通常采用相同的电路结构和参数［2］，为了提高效率，尽量降低在电能变换过程中的能量损耗，逆变器的控制结构多为单级式结构［5］，如图2所示，kc为电容电流有源阻尼系数。并网参考电流由最大功率点追踪（MPPT）产生的功率参考值和并网点电压经瞬时功率理论合成，以实现功率控制。

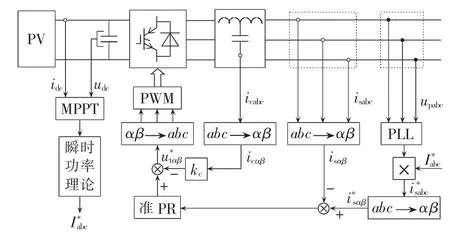
图2 两相静止坐标系下并网逆变器控制策略Fig.2 Control strategy of grid-connected inverter in two-phase stationary coordinates system

准PR控制器对正弦交流能够实现无静差控制［17］，因此本文采用准PR控制器来控制并网电流，其数学模型如式（1）所示。两相静止坐标系下α轴与β轴对称相同，因此仅以α轴为例进行分析，系统在复频域下的数学模型如图3所示。图中Gd（s）为数字控制过程中1.5拍延时的等效传递函数［11］，如式（2）所示。

其中，Tc为采样周期。

图3 系统复频域数学模型Fig.3 Mathematic model of system in complex frequency domain

根据文献［4］可以得到大型光伏电站α轴下的诺顿等效模型，如图4所示。可以看出，系统中既包含电流源与电压源之间的相互作用，又包含电流源与电流源之间的相互作用，显然根据单个并网逆变器的稳定性判据无法判别该复杂系统的稳定性。

图4 α轴下大型光伏电站诺顿等效模型Fig.4 Equivalent Norton model of LSPV in α axis

图中：

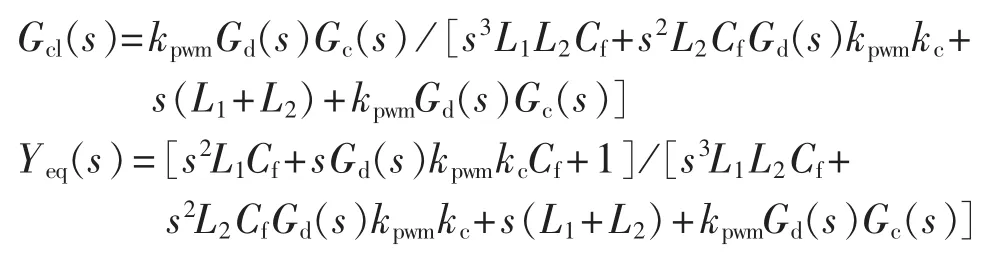
1.2 大型光伏电站导纳稳定性判据

根据叠加原理，由图4可以得到大型光伏电站中逆变器j的并网电流：

其中，Gj-j（s）为逆变器j对自身并网电流的影响系数；Gj-m（s）为逆变器m对逆变器j并网电流的影响系数；Gj-g（s）为电网电压对逆变器j并网电流的影响系数。经过整理可以将式（3）等效转化为：

由上式可知，当光伏电站中每台逆变器自身内部稳定且电网自身稳定时，系统的稳定性仅取决于：

可以看出，式（4）等效为前向通道为 1／n、反馈通道为 Yg（s） ／Yeq（s）的负反馈系统，环路增益为Yg（s）／［nYeq（s）］，记其为大型光伏电站的稳定性环路增益。因此可以得到大型光伏电站稳定性判据：光伏电站中每台逆变器自身内部稳定，即Gcl（s）不包含右半平面极点；电网自身内部稳定，即Yg（s）不包含右半平面极点；大型光伏电站的稳定性环路增益满足奈奎斯特稳定性判据。

以6台结构及参数相同的逆变器组成的大型光伏电站为分析算例，根据文献［18］设计的系统参数如表1所示。电网阻抗变化时，系统稳定性环路增益的奈氏曲线如图5所示。可以看出，当Lg=18μH时，系统运行于稳定状态，当Lg增加到19μH时，系统恰好进入不稳定状态，当Lg继续增加时系统稳定性进一步降低。

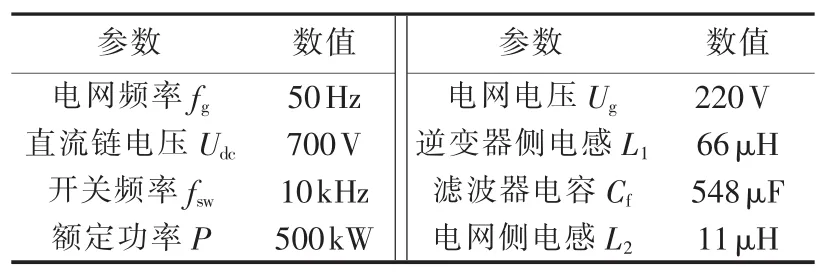
表1 系统参数Table 1 System parameters

图5 大型光伏电站稳定性环路增益的奈氏曲线Fig.5 Nyquist diagram of stability loop gain of LSPV

由上述分析可知，随着电网阻抗的增加，大型光伏电站的稳定性逐渐降低，最终进入不稳定运行状态。并且当电网导纳与系统闭环等效输出导纳相匹配时，会引发谐波谐振。因此有必要采取一定的措施提高大型光伏电站对电网阻抗变化的适应能力，抑制系统谐波谐振。

2 基于导纳重构的谐波谐振抑制策略

图6 不同电网阻抗时等效输出导纳和Yge（s）的伯德图Fig.6 Bode diagram of equivalent output admittance and Yge（s） for different grid impedances

对于大型光伏电站中的每台逆变器，其等效输出导纳的伯德图如图6所示，可以看出其相位曲线与90°线存在交点，交点处的频率为f1、f2。根据文献［6］可知，大型光伏电站中每台逆变器看到的等效电网导纳为 Yge（s）=Yg（s）／n，因此 Yge（s）的相位为-90°。 由图6 可以看出，随着 Lg的增大，Yge（s）幅值曲线与Yeq（s）幅值曲线的交截频率逐渐趋近于f2，并网电流的谐波含量将增大，且谐波频率主要集中在交截频率附近。当Lg增加到18.5μH时，两者的幅值曲线在 f2处交截，Yge（s）与 Yeq（s）处于并联谐振状态，此时并网电流中会出现大量f2频率附近的谐波，并网电流波形严重畸变，直至逆变器脱网停机。另外，由前文的稳定性判据可知，两者的幅值曲线在f2处交截时，大型光伏并网系统恰好处于临界不稳定状态。当Lg继续增大时，两者幅值曲线的交截频率小于 f2，系统进入不稳定运行状态。

如果采用一定的控制策略对Yeq（s）重新构造，使 Yeq（s）的幅值曲线不与 Yge（s）的幅值曲线相交，或者使 Yeq（s）的相位曲线不与 90°线相交，且距 90°线存在一定的裕度，那么就无法满足谐振产生的条件，可以避免由于电网阻抗变化而导致的谐波谐振。

本文提出一种将并网点电压反馈至电流控制器输出端的导纳重构方法，其控制结构如图7所示，由图可得导纳重构后的系统并网电流，如式（5）所示。

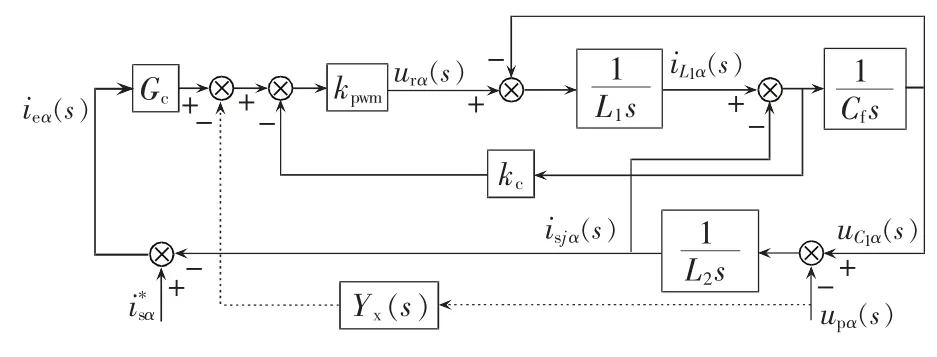
图7 输出导纳重构结构框图Fig.7 Block diagram of output admittance reshaping

由式（5）可得此时系统的等效输出导纳，如式（6）所示，相当于在系统原始输出导纳支路上并联了一个新的导纳Yeq_ne（s），系统等效模型如图8所示。

图8 输出导纳重构后的系统等效诺顿模型Fig.8 Equivalent Norton model of system after output admittance reshaping

由图8可知，理想情况下应使逆变器输出的基波电流不通过Yeq_re（s），而谐波电流要全部通过Yeq_re（s），因此输出导纳幅值重构的准则为：在基波频率处Yeq_re（s）的增益很小，以使基波电流不能通过；在谐波频率处Yeq_re（s）的增益很大，以使谐波电流全部通过。

根据导纳幅值重构准则易知，在Lg任意变化的过程中，不可能满足 Yeq_re（s）的幅频曲线不与 Yge（s）的幅频曲线相交。因此本文采用改变输出导纳相位的方法抑制谐波谐振，即Yeq_re（s）的相位在全频范围内不与90°线相交。如果将Yx（s）构造成简单的比例环节，只能通过调节Yeq_ne（s）的幅值来改变等效输出导纳的相位，无法同时满足幅值和相位的要求；若构造成积分环节，虽然使Yeq_ne（s）的相位有一定降低，但该相位不能调节，也相当于只能通过调节Yeq_ne（s）的幅值来改变等效输出导纳，难以满足设计要求。基于上述分析，本文将 Yx（s）构造成如式（7）所示的环节，该环节具有2个可调参数，k1用来调节Yx（s）的幅值，k2用来调节Yx（s）的相位和幅值，能够在较宽的频率范围内提供-90°附近的相位，可以实现对系统输出导纳相位的改善。

如果仅采用式（7）来构造输出导纳，虽能满足相位条件，但会使导纳在基频处的幅值较大，因此本文采用在式（7）中串联陷波器的方法来增加导纳在基频处的幅值衰减程度，其传递函数如式（8）所示［17］。

其中，ω0为陷波器的中心频率，本文即为基波角频率；Q为陷波器的自然模品质因数，Q值越小，陷波器在ω0处的幅值衰减越大，反之在ω0处的幅值衰减越小，综合考虑本文取Q值为0.707。

基于上述分析，本文最终将Yx（s）构造成如式（9）所示的传递函数，相比文献［14］的方法，该式不包含高次微分环节，工程中易于实现。

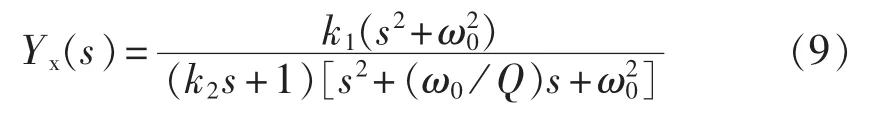
固定k1、k2中的一个，调节另一个时，系统等效输出导纳的伯德图如图9所示，可以看出，随着k1的增加，（f1，f2）频率段内的相位减小，低频段内的幅值增加，基频处的增益衰减程度有所减小，而随着k2的增加，幅相频率曲线的变化趋势正好与k1增加时相反；当k1太大或者k2太小时，基频以下频率段的相位将突变，且在基频附近穿越90°线；另外参数的变化对高频段几乎无影响。综合考虑，本例取k1=0.4、k2=0.06。

图9 参数变化时输出导纳的伯德图Fig.9 Bode diagram of output admittance for different parameters

采用导纳重构策略前后，逆变器输出导纳的伯德图如图10所示。可以看出，重构后逆变器等效输出导纳的相位曲线不再与90°线相交，且存有一定的裕度，在基频处的幅值有了更大的衰减，在低次谐波频率处的幅值有所提高，能够增强对低频谐波的抑制能力。因此导纳重构后系统不会由于电网导纳与逆变器等效输出导纳的交截而发生谐波谐振。

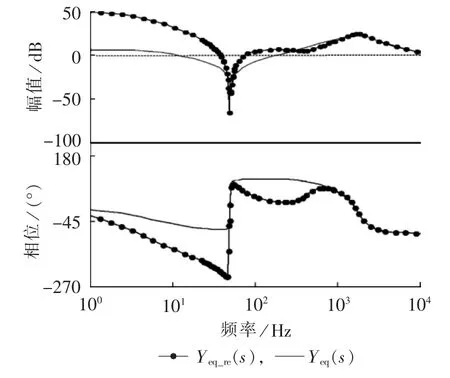
图10 导纳重构前后系统输出导纳伯德图Fig.10 Bode diagram of output admittance，before and after admittance reshaping

采用导纳重构策略后电网阻抗变化时，大型光伏电站的稳定性环路增益奈氏曲线如图11所示。可以看出，随着电网阻抗的增加，奈氏曲线始终不包围（-1，j0）点，且始终不包含右半平面极点，因此系统始终处于稳定运行状态。这说明导纳重构策略提高了系统稳定性，增强了系统对电网阻抗变化的适应能力。

图11 导纳重构后光伏电站稳定性环路增益奈氏曲线Fig.11 Nyquist curve of stability loop gain of LSPV after admittance reshaping

3 仿真结果

为了验证本文理论分析的正确性，根据图1、2所示的原理图搭建额定功率为3MW的大型光伏电站仿真模型，逆变器参数如表1所示。由于所有逆变器均相同，仅对1号逆变器的仿真结果进行分析。

图12、13 为原始系统在 Lg分别取 10 μH、70 μH情况下的系统并网电流。由图12可以看出，Lg取10μH时逆变器的并网电流谐波含量较小，满足并网要求，与前面分析的系统处于稳定状态相符合；谐波主要集中在550Hz附近，与逆变器输出导纳幅值曲线和电网导纳幅值曲线的交截频率551Hz相吻合。当Lg增加到70μH时，由图13可以看出逆变器并网电流谐波含量增大，不满足并网要求，与前面分析的系统处于不稳定状态相符合；谐波主要集中在250Hz附近，与逆变器输出导纳幅值曲线和电网导纳幅值曲线的交截频率244Hz相吻合。

图12 Lg取10 μH时系统并网电流Fig.12 Grid-connecting current of system when Lgis 10 μH

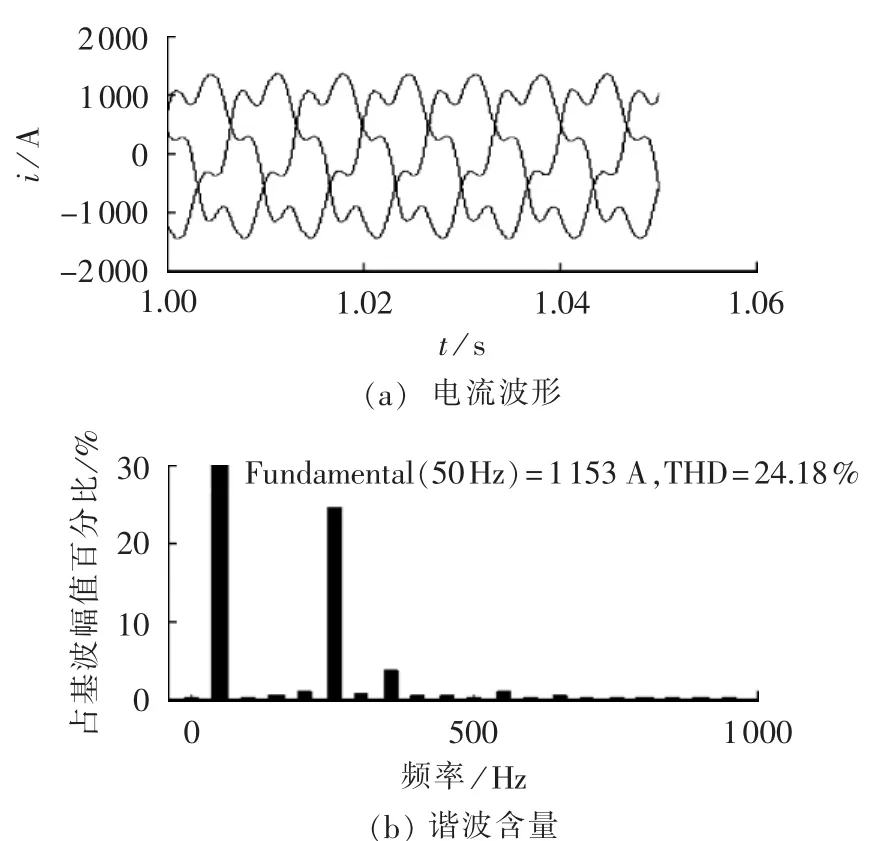
图13 Lg取70 μH时系统并网电流Fig.13 Grid-connecting current of system when Lgis 70 μH

图14为原始系统分别处于谐振状态（Lg=18.5μH）和不稳定状态（Lg=70μH）情况下，在t=1.06s时向所有逆变器中加入导纳重构策略前后的系统并网电流波形。可以看出，采用导纳重构策略后2种状态下的并网电流谐波都得到了很好的抑制，电流波形均变好，谐波含量较小，满足并网要求。这说明导纳重构策略提高了系统稳定性，能很好地抑制谐波谐振。

图14 系统并网电流仿真波形Fig.14 Simulative waveforms of system grid-connecting current

4 实验结果

为了进一步验证理论分析的正确性，同时考虑到实验条件等因素，现仅以2台电路结构、参数相同的三相LCL型并网逆变器为例进行实验分析。实验主要参数根据文献［18］进行设计，如表2所示。2台逆变器采用相同的控制策略，其中导纳重构策略的参数取为：k1=1、k2=0.04。由于2台逆变器相同，仅以其中一台的实验结果为例进行分析。

表2 实验系统电路参数Table 2 Circuit parameters of test system

图15为不采用任何抑制策略情况下，Lg取2.8mH时的实验波形，根据前文分析可以判断此时系统处于谐振状态。可以看出，并网电流中含有大量11次频率附近的谐波，与逆变器输出导纳幅值曲线和电网导纳幅值曲线的交截频率581Hz相符合。

图15 电网阻抗为2.8 mH时原始系统实验波形Fig.15 Experimental waveforms of original system when Lgis 2.8 mH

图16为原始系统分别处于谐振状态（Lg=2.8mH）和不稳定状态（Lg=4mH）情况下，采用本文所提导纳重构策略后的实验波形。对比图15和图16（a）可以看出，采用导纳重构策略后，系统中的11次频率附近的谐波得到了很好的抑制，且3、5、7次等低频谐波含量较小，满足并网要求。由图16（b）可以看出，原本处于不稳定状态的系统，采用导纳重构策略后进入稳定状态，并网电流波形良好，谐波含量较小，满足并网要求。这说明导纳重构策略提高了系统稳定性，对谐波谐振具有很好的抑制作用，增强了系统对电网阻抗变化的适应能力。

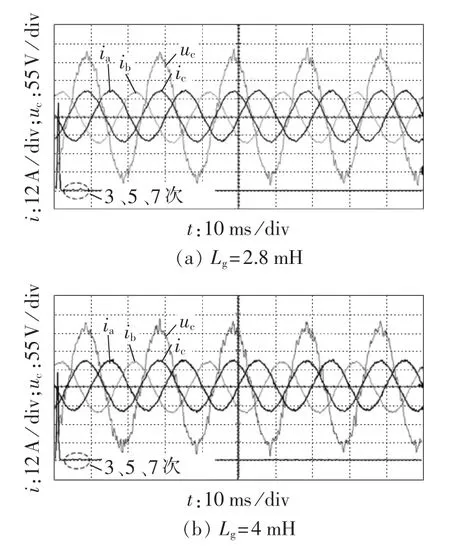
图16 采用导纳重构策略时的实验波形Fig.16 Experimental waveforms，with admittance reshaping strategy

5 结论

本文推导出一种基于系统导纳的大型光伏电站稳定性判据，并分析了电网阻抗对系统稳定性的影响，提出一种基于导纳重构的大型光伏电站谐波谐振抑制策略，主要得到以下结论。

a.当大型光伏电站内各逆变器稳定，且电网自身稳定时，大型光伏并网系统的稳定性取决于其稳定性环路增益是否满足奈奎斯特稳定性判据。

b.电网阻抗的增加使系统稳定性降低，并网电流谐波含量增大，且谐波集中在电网导纳幅值曲线与逆变器输出导纳幅值曲线的交截频率附近；当输出导纳在其幅值曲线与电网导纳幅值曲线交截频率处的相位为90°时，系统处于谐振状态，电网阻抗继续增加时系统进入不稳定状态。

c.为使光伏电站不受电网阻抗的影响，理想情况下逆变器等效输出导纳在基频处的幅值应为无穷小，在谐波频率处的幅值应为无穷大，相位曲线在全频范围内不与90°线相交，且存在一定裕度。根据该准则设计的导纳重构策略能够提高光伏电站的稳定性，增强其对电网阻抗变化的适应能力，进而抑制谐波谐振的发生。

［1］赵争鸣，雷一，贺凡波，等.大容量并网光伏电站技术综述［J］.电力系统自动化， 2011，35（12）：101-107.ZHAO Zhengming，LEI Yi，HE Fanbo，et al.Overview of large-scale grid-connected photovoltaic power plants［J］.Automation of Electric Power Systems，2011，35（12）：101-107.

［2］RUB’EN I，TAKESHI S，YOSUKE F，et al.Parallel connection of grid-connected LCL inverters for MW-scaled photovoltaic systems［C］∥2010 International Power Electronics Conference （IPEC）.Sapporo，Japan：IEEE，2010：1988-1993.

［3］周林，张密.大型光伏电站谐振现象分析［J］.电力自动化设备，2014，34（6）：8-14.ZHOU Lin，ZHANG Mi.Analysis of resonance phenomenon in large-scale photovoltaic power plant［J］.Electric Power Automation Equipment，2014，34（6）：8-14.

［4］杨明，周林，张东霞，等.考虑电网阻抗影响的大型光伏电站并网稳定性分析［J］. 电工技术学报，2013，28（9）：214-223.YANG Ming，ZHOU Lin，ZHANG Dongxia，et al.Stability analysis of large-scale photovoltaic power plants for the effect of grid impedance［J］.Transactions of China Electrotechnical Society，2013，28（9）：214-223.

［5］周林，张密，居秀丽，等.电网阻抗对大型并网光伏系统稳定性影响分析［J］. 中国电机工程学报，2013，33（34）：34-41.ZHOU Lin，ZHANG Mi，JU Xiuli，et al.Stability analysis of largescale photovoltaic plants due to grid impedances［J］.Proceedings of the CSEE，2013，33（34）：34-41.

［6］AGORRETA J L，BORREGA M，LÓPEZ J，et al.Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants［J］.IEEE Transactions on Power Electronics，2011，26（3-4）：770-785.

［7］HE J W，LI Y W，BOSNJAK D，et al.Investigation and active damping ofmultiple resonancesin a parallel-inverter-based microgrid［J］.IEEE Transactions on Power Electronics，2013，28（1）：234-246.

［8］MARCO L，REMUS T，FREDE B.Stability of grid-connected PV inverters with large grid impedance variation［C］∥Power Electronics Specialisis Conference.Bari，Italy：IEEE，2004：4773-4779.

［9］SUN J. Impedance-based stability criterion for grid-connected inverters［J］.IEEE Transactions on Power Electronics，2011，26（11）： 3075-3078.

［10］李小强，伍小杰，耿乙文，等.感性电网阻抗下三相光伏逆变器稳定性分析［J］.中国电机工程学报，2014，34（18）：2906-2916.LI Xiaoqiang，WU Xiaojie，GENG Yiwen，et al.Stability analysis of three-phase PV inverter under inductive grid impedance condition［J］.Proceedings of the CSEE，2014，34（18）：2906-2916.

［11］WANG X，BLAABJERG F，LISERRE M，et al.An active damper for stabilizing power electronics based AC systems［J］.IEEE Transactions on Power Electronics，2014，29（7）：3318-3329.

［12］PEÑA-ALZOLA R，LISERRE M，BLAABJERG F，et al.A selfcommissioning notch filter for active damping in a three-phase LCL-filter-based grid-tie converter［J］.IEEE Transactions on Power Electronics，2014，29（12）：6754-6761.

［13］CESPEDES M，SUN Jian.Adaptive control of grid-connected inverters based on online grid impedance measurements［J］.IEEE Transactions on Sustainable Energy，2014，5（2）：516-523.

［14］YANG Dongsheng，RUAN Xinbo，WU Heng.Impedance shaping of the grid-connected inverterwith LCL filterto improve its adaptability to the weak grid condition［J］.IEEE Transactions on Power Electronics，2014，29（11）：5795-5805.

［15］曾正，赵荣祥，吕志鹏，等.光伏并网逆变器的阻抗重塑与谐波谐振抑制［J］. 中国电机工程学报，2014，34（27）：4547-4558.ZENG Zheng，ZHAO Rongxiang，LU¨Zhipeng，et al.Impedance reshaping of grid-tied inverters to damp the series and parallel harmonic resonances of photovoltaic systems［J］.Proceedings of the CSEE，2014，34（27）：4547-4558.

［16］陈新，张旸，王赟程.基于阻抗分析法研究光伏并网逆变器与电网的动态交互影响［J］. 中国电机工程学报，2014，34（27）：4559-4567.CHEN Xin，ZHANG Yang，WANG Yuncheng.A study of dynamic interaction between PV grid-connected inverters and grid based on the impedance analysis method［J］.Proceedings of the CSEE，2014，34（27）：4559-4567.

［17］赵清林，郭小强，邬伟扬.单相逆变器并网控制技术研究［J］.中国电机工程学报，2007，27（16）：60-64.ZHAO Qinglin，GUO Xiaoqiang，WU Weiyang.Research on control strategy for single-phase grid-connected inverter［J］.Proceedings of the CSEE，2007，27（16）：60-64.

［18］LISERRE M，BLAABJERG F，HANSEN S.Design and control of an LCL-filter-based three-phase active rectifier［J］.IEEE Transactions on Industry Applications，2005，41（5）：1281-1291.