计及分布式电源和负荷不确定性的多目标配网重构

王薪苹，卫志农，孙国强，李逸驰，臧海祥

（河海大学 能源与电气学院，江苏 南京 211100）

0 引言

配网重构技术作为未来实施智能电网的基础，是配电自动化的关键技术之一，其在保障电能质量、降低网络损耗等方面有着重要作用。在研究配网重构的初始阶段，主要以配网的某一项评估指标作为优化目标［1-2］，随着研究不断深入，对于单目标重构的研究趋于完善。然而，配网重构实际上是一个复杂的非线性多目标组合优化问题，近期国内外学者对此有一些研究。文献［3］以降低网损和减少开关操作次数为综合优化目标构建配网多目标动态重构模型，阐明了配网重构降损效果同开关操作次数之间的最佳均衡关系，但未考虑电压质量和负荷的均衡度。文献［4］通过负荷均衡和支路交换相结合实现了配网重构的多目标优化，达到了均衡负荷和降低网损的目的，但目标函数中并没有考虑到电压质量。文献［5］结合人工免疫算法与非支配等级概念，同时优化有功损耗和可靠性指标，然而，考虑可靠性后，应该确保有较高的电压质量，因此，有必要将电压质量指标计入目标函数集中。

此外，近年来风电等新能源并网速度的加快，使得配网中不确定性因素显著增加，为了使重构研究更加符合实际情况，在建模优化过程中，需要合理地处理新能源出力等其他不确定性因素。文献［6］建立了基于非支配解排序粒子群算法的多目标配网重构模型，其处理风电和太阳能出力的方法较为简单，没有充分考虑分布式电源（DG）的不确定性。文献［7］采用点估计法处理风电和光伏出力的不确定性，采用自适应粒子群算法求解多目标模型，较好地处理了计及不确定因素的多目标配网重构问题，相比本文采用的场景分析法，其随机模型较为复杂。

基于上述分析，本文首先介绍了场景分析法的2个关键问题，即场景数的确定方法与场景综合指标定义，给出了本文3个优化目标的定义：有功损耗、节点最小电压值、负荷均衡度，构建了多目标配网重构模型。其次，详细介绍了风电机组出力和光伏出力模型，以及对负荷不确定性的处理策略，接着详细介绍了多目标扰动生物地理学优化MDBBO（Multiobjective Disturbance Biogeography-Based Optimization）算法的求解流程。最后，在对多目标算法性能分析的基础上，算例分析了风电和光伏并网以及场景数对多目标网络重构的影响，使得整个网络重构过程更加符合实际情况。

1 基于场景分析法的多目标配网重构模型

1.1 场景数确定策略及方案综合最优性的评价

场景分析法能够高效地解决随机性问题［8］。该方法的核心思想是将不确定性因素转化到确定性场景中来，从而使模型得到简化，提高运算效率。风电、光伏并网后，配网重构中不确定性因素主要来自3个方面：风电机组输出功率、太阳能电池板输出功率、负荷，因而重构模型中选择的场景是以上三者所含场景的组合。本文采用同步回代缩减SBR（Simultaneous Backward Reduction）法对大规模的场景进行削减［9］，避免场景组合爆炸，其核心思想是使缩减前后场景集合之间的概率距离最小。对于方案的综合性能，最常用的一种评估方法是：比较基于场景发生概率的目标函数期望值大小［10］，如式（1）所示。

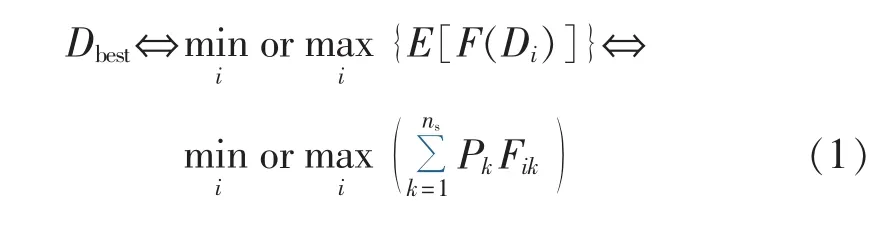
其中，ns为削减后的场景数；Pk为场景k发生的概率；Fik为第k个场景下第i个优化方案的综合评价值；Di为第 i个优化方案；E［F（Di）］为第 i个优化方案的目标函数期望值。

1.2 多目标配网重构模型

（1）配网系统有功损耗表达式为：

其中，Nb为支路数；Rk为支路k的电阻；Pk为支路k的有功功率；Qk为支路k的无功功率；Uk为支路k的末端电压。

（2）电压质量评价指标，使电压最低节点电压最大化，即：

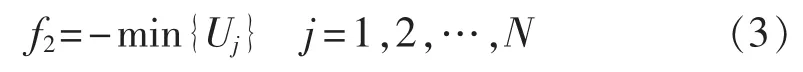
其中，N为节点数。

（3）负荷均衡是指通过网络重构将负荷较重线路上的部分负荷转移到负荷较轻的线路上，该目标定义为系统负荷均衡度指数（SLBI），其值越小越好，用式（4）进行衡量：

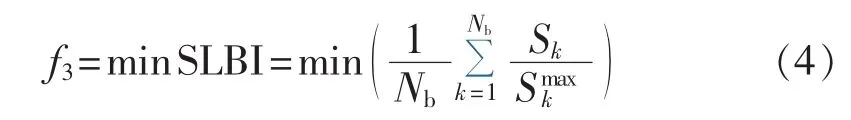
其中，Sk为流经支路k的实际电流大小；Skmax为允许流经支路k的最大电流。

针对每个重构方案，计算每一个场景下上述3个指标值，按照式（1）求出每个目标的期望值，按式（5）进行综合，在本文所用的MDBBO算法中，式（5）定义为综合评价指标，用来引导种群进化。

其中，F为栖息地适宜度向量；fi为栖息地第i个目标函数值向量；fi，max、fi，min分别为所有栖息地第 i 个目标的最大、最小值；Arank为栖息地非支配等级向量；δratio为种群中非支配等级为1的个体所占的比例，迭代前期，支配等级为1的个体较少，支配等级在综合指标中所占比重较大，随着种群迭代进化，非支配等级为1的个体越来越多，支配等级在综合评价指标中的作用降低；w1、w2、w3初始值均设置为 1，根据对各目标的重视程度，可以灵活设置权重，三者的和为1。

潮流计算中，还需要考虑以下约束条件：

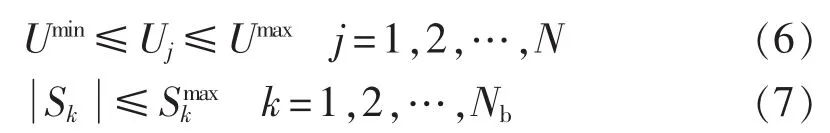
其中，Umax、Umin分别为配网正常运行时节点电压的上、下限；为支路k的最大载流量。

2 分布式电源及负荷不确定性的处理

2.1 风机及光伏出力场景划分

图1是风电机组输出功率与风速的关系曲线，其中，vi、vr、vo分别为风机切入风速、额定风速和切出风速，Pr为风机额定输出功率。

图1 风电机组功率特性曲线Fig.1 Power characteristic curve of wind turbine-generator set

目前一般认为风速v服从Weibull分布［11］，如式（8）所示。

其中，c和d分别为尺度参数和形状参数，可以根据现场实测风速的历史数据辨识。在已知风速随机分布参数的条件下，可以求出任意风速区间的概率，计算公式如下：

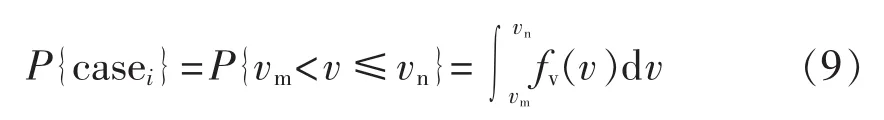
其中，casei表示第i个场景；vn和vm分别为风速场景区间的上、下边界。

太阳光照强度可以近似看成服从Beta分布［11］：

其中，s和smax分别为一时间段内的实际光强和最大光强（W／m2）；α和β为一段时间内服从Beta分布的形状参数。

太阳能电池方阵输出功率为：

其中，A为太阳能电池方阵总面积；δ为光电转化效率。

采用与风电机组出力同样的场景划分方法，划分光强区间，根据光强概率密度函数计算不同区间（场景）的概率。

本文将单台风机和单个光伏接入点分别划分为5个典型场景；由于同一地区的风光差异不大，机组选择同种型号，多台机组可以采用单台机组划分场景的策略；输出功率取为相应风速和光强范围内输出功率的平均值。

风电机组和太阳能电池板方阵所在节点可简化处理为PQ节点，并假设可以通过电容器的自动投切保持功率因数不变，则无功功率可按式（12）求得。

其中，ψ为功率因数角。

2.2 负荷不确定性的处理

配电网络中，日负荷曲线、月负荷曲线和年负荷曲线都有较大的波动，随着分布式电源并网，负荷预测更加困难，因此使得配网重构中的不确定性更强。本文将负荷分为3个典型场景：常态负荷场景、低负荷场景、高负荷场景。

3 基于MDBBO算法的求解流程

标准测试函数表明：生物地理学优化BBO［12］（Biogeography-Based Optimization）算法具有实现简单、搜索精度高、参数少、收敛速度快等优点。在BBO算法中，主要有迁移和突变2个操作。通过迁移操作可共享栖息地间的信息，共同向着目标方向进化；通过变异操作，能够保障栖息地个体的多样性。

本文在基本BBO算法的基础上，采用扰动迁移算子和余弦迁移模型，根据最小化各子目标的原则设计栖息地适宜度评价指标以引导种群进化，用归档种群保存进化过程中的非支配解，并用循环拥挤距离法对归档种群实时更新，最后用相同体检测策略剔除进化过程中产生的相同解，从而形成MDBBO算法［13］，用以解决多目标配网重构问题。由于多目标Pareto解集中不止一个解，本文采用模糊集理论［14］来确定最佳决策解。

3.1 扰动迁移算子

用轮盘赌确定第k个栖息地的第j个变量迁移到第i个栖息地的第j个变量位置后，随机生成k1、k2ϵ｛1，2，…，Np｝／｛i｝，Np为种群规模。 按式（13）对迁移进行扰动。

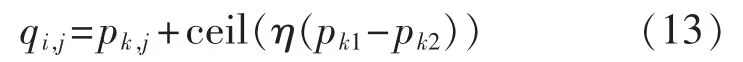
其中，η 为 0～1 间的随机数；ceil（·）表示向正无穷方向取整。

3.2 余弦迁移模型

文献［15］对比分析了6个线性和非线性种群迁移模型，标准算例测试结果表明，复杂的迁移模型比线性迁移模型更加符合客观规律，寻优性能更佳。因此，本文使用如图2所示的余弦迁移模型来替换标准BBO算法中的线性迁移模型。由图2可知，当栖息地中物种数较少或较多时，迁入率λ和迁出率μ的变化相对比较平稳，而当栖息地物种数量处于中等时，λ和μ的变化相对较快。该模型的计算公式如下：

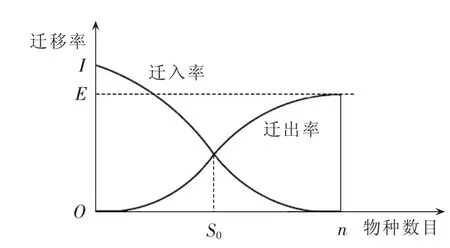
图2 余弦迁移模型Fig.2 Cosine migration model

其中，I和E分别为最大迁入率、最大迁出率；λk和μk分别为第k个栖息地的迁入率、迁出率。

3.3 网络简化及编码

基于智能算法的配网重构在种群初始化和迭代过程中，将会产生大量的不可行解，即重构后网络拓扑结构不满足辐射状的解。不可行解占据大量的搜索空间，使得常规搜索方法的效率大幅降低。本文采用基于独立环路［16］的编码策略可以有效地减少变量维数。同时，利用图论中连通度理论［17-18］对不可行解进行辨识，使得解满足网络呈辐射状的约束条件，算法流程图如图3所示。

图3 多目标扰动生物地理学优化算法流程图Fig.3 Flowchart of MDBBO algorithm

4 算例分析

4.1 算法性能分析

本文使用文献［19］所给的69节点配网系统，该配网系统含有73条支路、5个基本环，基准功率为 10 kV·A，基准电压为 12.66 kV，全系统的负荷为3.9MW和2.7 Mvar。每条支路的载流量分别为：支路1—9为400 A，支路46—49和52—64均为300 A，其他支路均为200 A。初始条件下，支路69、70、71、72、73断开，网损为 224.93 kW。 使用 MATLAB R2013a 编写程序，计算环境为：Intel（R）Core（TM）i3-2120CPU@3.30 GHz，4GB RAM。

MDBBO算法参数设置如下：种群规模Np=70，最大迭代次数Kmax=50，最大突变率mmax=0.05，最大迁入、迁出率均取1，即E=I=1。

由于Pareto解集中解的个数比较少，文献［19］给出了分别以各个子目标为主要目标的测试结果，为了便于比较，本文采取同样的优化方式，优化结果对比如表1—3所示，表中，方案一列中14／57／61／69／70 表示断开的支路为 14、57、61、69、70，具体编号见文献［19］；Umin为标幺值，后同。

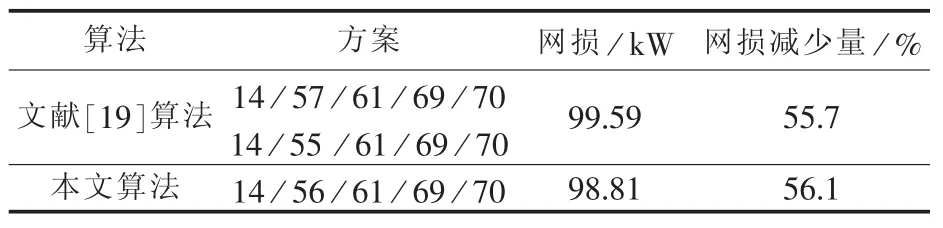
表1 网损优化结果Table 1 Results of net-loss optimization

表2 电压质量优化结果Table 2 Results of voltage quality optimization

表3 负荷均衡度优化结果Table 3 Results of load balancing degree optimization

从表1—3的优化结果中可以看出，本文在分别以不同子目标为主要目标的优化中，优化结果更好，在网络有功损耗、电压质量、负荷均衡三方面分别较初始网络状态提高了56.1%、4.4%、22.9%。特别是在负荷均衡度上，较文献［19］提高了8.7%，从而验证了MDBBO算法在求解多目标配网重构问题方面的可行性与有效性。

本文给出网损目标期望值的收敛曲线如图4所示。由图4可见，算法在迭代11次后进入收敛状态，具有较好的收敛性。

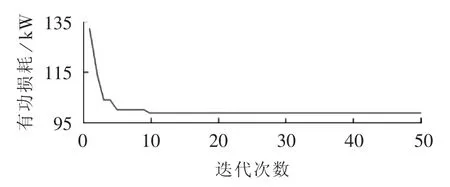
图4 网损收敛曲线Fig.4 Net-loss convergence curve

4.2 计及分布式电源的多目标配网重构

算例选取及算法参数设置同4.1节。风机和太阳能分布参数 d=1.99，c=9.94，α=0.28，β=2.05。 风机的切入、额定、切出风速分别为 3m／s、14m／s、25 m／s，额定功率为400 kW；光伏电池方阵单个组件面积为2.16m2，光电转换效率为13.44%，400个组件组成一个光伏电池方阵，最大日照强度为0.5W／m2。分别在节点8、13、18处接入3台风力发电机，在节点20、26、29处分别接入50个光伏电池方阵。高、低负荷分别为常规负荷的1.1倍、90%，高、低负荷概率均取0.2，常规负荷概率取0.6。表4为重构方案对比结果，表中指标值均为期望值，方案为模糊化后的最终决策方案，表5中同。

表4 重构方案对比Table 4 Comparison among reconfiguration schemes

由表4可知，不计及分布式电源的多目标重构结果相比原始网络下的各指标都有较大的提升，有功损耗降低52.97%，最小电压提升4.3%，负荷均衡度降低19.47%，重构优化结果较明显。计及分布式电源的多目标重构使得网损和负荷均衡度进一步降低，相比不计及分布式电源的重构，这2项指标分别降低了14.45%和7.14%。图5为节点电压分布（标幺值），图中，不计及分布式电源的重构的网络节点电压相比原始网络有较大提升，计及分布式电源后，部分节点的电压相比不计及分布式电源的优化结果有进一步提升，从而表明，适当的分布式电源并网和优化重构，不仅消纳了可再生能源，而且能够明显改善系统的各项指标。

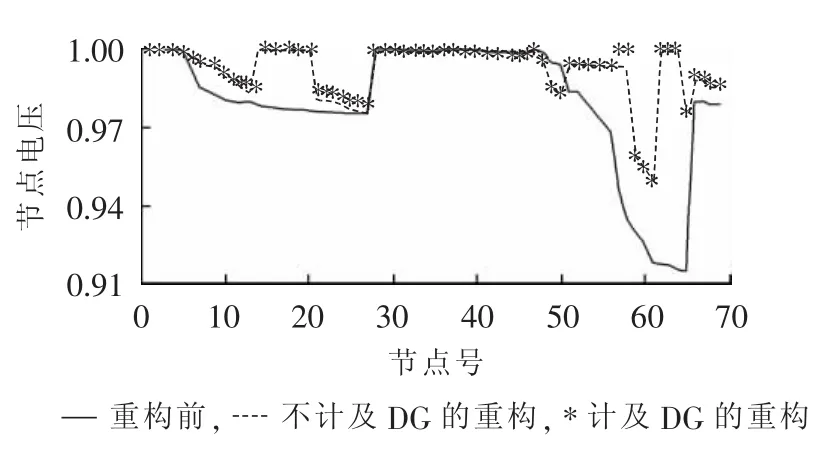
图5 电压分布图Fig.5 Voltage distribution

4.3 场景数对优化结果的影响

在削减场景的过程中，需要确定最终场景数，表5给出了3个场景数下的重构优化结果。由表可知，当场景数较少时，有功损耗较多，负荷均衡度较低，计算时间较短；场景数较大时，有功损耗较低，负荷均衡度较高，但是计算时间较长；不同场景数对最小电压没有影响。综上，本文场景数取30较为合理，均衡考虑了各项指标。

表5 不同场景数下的优化结果Table 5 Results of optimization for different scenario numbers

5 结论

本文提出了计及分布式电源和负荷不确定性的多目标配网重构模型，该模型充分地考虑了风电出力、光伏发电以及负荷的不确定性，同时优化了配网的多个重要指标，相比以往的重构研究，网络优化更符合实际决策过程。算例测试表明：MDBBO算法求解模型具有较高的搜索效率；在配网消纳可再生能源的同时，通过网络重构技术，能够较明显地降低网络损耗、提升节点电压、均衡线路上的负荷分布，从而验证了本文所提模型的有效性与实用性。然而，由于分布式电源的接入，将对网络供电的可靠性造成潜在威胁，在接下来的研究工作中将会重点考虑。

［1］卫志农，王丹，孙国强，等．基于动态粒子群优化算法的配电网动态重构研究［J］．中国电机工程学报，2005，25（增刊 1）：93-98．WEI Zhinong，WANG Dan，SUN Guoqiang，et al．Research of dynamic reconfiguration of feeder based the dynamic particle swarm optimization algorithm［J］．Proceedings of the CSEE，2005，25（Supplement 1）：93-98．

［2］胡卫，黄纯，孙彦广，等．基于人工培植杂交的配电网重构方法［J］．电力自动化设备，2014，34（9）：106-111．HU Wei，HUANG Chun，SUN Yanguang，et al．Distribution of network reconfiguration based on artificial cultivated hybrid［J］．Electric Power Automation Equipment，2014，34（9）：106-111．

［3］孙惠娟，彭春华，袁义生．综合开关次数分析的配电网多目标动态重构［J］．电力自动化设备，2014，34（9）：41-46．SUN Huijuan，PENG Chunhua，YUAN Yisheng．Multi-objective dynamic distribution network reconfiguration considering switching frequency［J］．Electric Power Automation Equipment，2014，34（9）：41-46．

［4］孙健，江道灼．一种多目标配电网络重构新算法［J］．电力系统自动化，2003，27（20）：57-61．SUN Jian，JIANG Daozhuo．A new multi-objective algorithm for distribution network reconfiguration［J］．Automation of Electric Power Systems，2003，27（20）：57-61．

［5］ALONSO F R，OLIVEIRA D Q， ZAMBRONID S A C．Artificial immune systems optimization approach for multiobjective distribution system reconfiguration ［J］．IEEE Transactions on Power Systems，2015，30（2）：840-847．

［6］TULADHAR S R，SINGH J G，ONGSAKUL W．A multi-objective network reconfiguration of distribution network with solar and wind distributed generation using NSPSO［C］∥2014 International Conference on Green Energy for Sustainable Development.Cape Town，South Africa：IEEE，2014：1-7．

［7］MALEKPOUR A R，NIKNAM T，PAHWA A，et al．Multi-objective stochastic distribution feeder reconfiguration in systems with wind power generators and fuel cells using the point estimate method［J］．IEEE Transactions on Power Systems，2013，28（2）：1483-1492．

［8］何禹清，彭建春，文明，等．含风电的配电网重构场景模型及算法［J］．中国电机工程学报，2010，30（28）：12-18．HE Yuqing，PENG Jianchun，WEN Ming，et al．Scenario model and algorithm for the reconfiguration of distribution network with wind power generators［J］．Proceedings of the CSEE，2010，30（28）：12-18．

［9］张晓辉，闫柯柯，卢志刚，等．基于场景概率的含风电系统多目标低碳经济调度［J］．电网技术，2014，38（7）：1835-1841．ZHANG Xiaohui，YAN Keke，LU Zhigang，et al． Scenario probability based multi-objective optimized low-carbon economic dispatching for power grid integrated with wind farms ［J］．Power System Technology，2014，38（7）：1835-1841．

［10］陈海焱，陈金富，段献忠．含风电机组的配网无功优化［J］．中国电机工程学报，2008，28（7）：40-45．CHEN Haiyan，CHEN Jinfu，DUAN Xianzhong．Reactive power optimization in distribution system with wind power generators［J］．Proceedings of the CSEE，2008，28（7）：40-45．

［11］王成山，郑海峰，谢莹华，等．计及分布式发电的配电系统随机潮流计算［J］．电力系统自动化，2005，29（24）：39-44．WANG Chengshan，ZHENG Haifeng，XIE Yinghua，et al．Probabilistic power flow containing distributed generation in distribution system［J］．Automation of Electric Power Systems，2005，29（24）：39-44．

［12］SIMON D．Biogeography-based optimization［J］．IEEE Transactions on Evolutionary Computation，2008，12（6）：702-713．

［13］徐志丹，莫宏伟．多目标扰动生物地理学优化算法［J］．控制与决策，2014，29（2）：231-235．XU Zhidan，MO Hongwei．Multi-objective disturbance biogeography based optimization algorithm［J］．Control and Decision，2014，29（2）：231-235．

［14］FARINA M，AMATO P．A fuzzy definition of optimality for many-criteria optimization problems［J］．Systems，Man and Cybernetics，Part A：IEEE Transactions on Systems and Humans，2004，34（3）：315-326．

［15］MA H．An analysis of the equilibrium of migration models for biogeography-based optimization［J］．Information Sciences，2010 ，180（18）：3444-3464．

［16］李振坤，陈星莺，余昆，等．配电网重构的混合粒子群算法［J］．中国电机工程学报，2008，28（31）：35-41．LI Zhenkun，CHEN Xingying，YU Kun，et al．Hybrid particle swarm-optimization for distribution network reconfiguration ［J］．Proceedings of the CSEE，2008，28（31）：35-41．

［17］FIEDLER M．Algebraic connectivity of graphs［J］．Czechoslovak Mathematical Journal，1973，23（2）：298-305．

［18］管宇，张晓东，徐光辉．树的变形与代数连通度［J］．应用数学学报，2011，34（2）：341-352．GUAN Yu，ZHANG Xiaodong，XU Guanghui．Deformation and algebraic connectivity of weighted trees ［J］．Acta Mathematicae Applicatae Sinica，2011，34（2）：341-352．

［19］ELDURSSI A M，O’CONNELL R M．A fast non-dominated sorting guided genetic algorithm for multi-objective power distribution system reconfiguration problem［J］．IEEE Transactions on Power Systems，2015，30（2）：593-601．