基于BPSOGA的含风电机组的配电线路故障区段定位

金 涛，李鸿南，刘 对

（福州大学 电气工程与自动化学院，福建 福州 350116）

0 引言

随着世界能源危机和环境污染的加重，人们开始关注更洁净、可再生、高效的电源——分布式电源 DG（Distributed Generator）［1-2］。然而 DG 的接入使得配电系统从单电源辐射状网络变为功率双向流动的复杂多端电源网络［3-4］。此外，配电系统的结构和潮流等也随之发生变化，这给配电线路的故障定位造成了一定的影响。因此，以单电源辐射状为基础的配电网络故障区段定位方法因受到DG的影响而需要改进和完善［5］。对于在分段开关或联络开关处配备馈线终端单元FTU（Feeder Terminal Unit）的配电线路，可将其收集的故障信息上传至数据采集与监视控制系统（SCADA），启动故障定位软件判断故障区段［6-7］。但由于配电线路中经常发生多重故障，且FTU安装在户外，受恶劣环境等因素的影响，其上传的故障信息经常发生畸变，使得上传的信息无法正确反映故障情况，因此急需研究出具有高准确性和容错性的故障区段定位算法。

国内外学者针对未接入DG的传统配电网故障区段定位提出了多种定位方法［8-9］。有关接入DG后配电线路的故障区段定位方法也有相应的研究。文献［10］在利用FTU采集信息的基础上，对配电线路的开关函数和适应度函数进行改进，提出在配电线路投入多端电源和发生多重故障下的故障区段定位方法。但是，这些方法在故障定位时需要多次假定故障电流正方向，给算法的编码和故障定位带来诸多麻烦。文献［11］提出假定每个开关的上游电源和下游电源、上游线路和下游线路，再根据改进的遗传算法GA（Genetic Algorithm）和配电线路数学模型进行区段定位，但该方法在开关上游具有多个电源时会造成同一个开关上游线路和下游线路的重叠，不利于定位；文献［12］提出根据故障电流信息改进的故障区段定位方法，但该文只将DG集中接在出线开关处，且短路电流均按DG出口三相短路时的最大短路电流计算，这些假定条件太苛刻，不利于该方法的广泛使用。其他学者也在不同文献中对此问题展开了广泛有益的研究［13-14］。

本文对整个配电线路开关统一假定网络正方向（主电源指向线路），使得每个开关都有明确的上下游线路。考虑风电机组的并入和负荷时变性，对配电线路的开关函数和适应度函数进行改进。针对普通智能算法普遍存在的“未成熟收敛”问题，本文提出一种基于二进制粒子群优化BPSO（Binary Particle Swarm Optimization）算法和GA的混合算法（BPSOGA）的定位方法。该方法利用双种群进化和信息交换的策略对本文所建立的含风电机组的配电线路故障区段定位数学模型进行求解，减少故障定位过程中出现“未成熟收敛”的概率，提高故障区段定位的准确性和容错性，且收敛速度得到有效提升。

1 配电线路故障区段定位关键技术

配电线路发生故障时，FTU可检测到故障电流，由于风电机组等DG的投入，使得网络功率双向流动。如图1（a）所示，规定主电源到线路的方向为整个网络的唯一正方向，当正方向k1点发生短路故障时，流过FTU1的短路电流I=Ik1，方向与正方向一致，滞后于母线电压U一个相角φk1（φk1为母线到k1之间的阻抗角），如图 1（b）所示，0°＜φk1＜90°，此时故障电流方向为正，短路功率为正；当反方向k2点发生短路故障时，流过FTU1的短路电流I=-Ik2，方向与正方向相反，滞后于母线电压U一个相角180°+φk2（φk2为母线到 k2之间的阻抗角），如图 1（c）所示，180°＜180°+φk2＜270°，此时故障电流为负，短路功率为负。因此可以通过判别短路功率方向来判别故障电流方向。

图1 故障电流检测工作原理Fig.1 Principle of fault current detection

开关处FTU检测过流信号的编码方式如下：

其中，si为区段Si的区段状态编码。在图2所示含风电机组的配电线路中，区段S3发生短路故障，开关1、2、3上的FTU检测到正方向的故障电流，开关4、5上的FTU检测到负方向的故障电流，开关状态编码为［1 1 1-1-1］，区段状态编码为［0 0 1 0 0］。

其中，Ij（j=1，2，…，D）为第 j个开关状态编码，D 为开关总数。

同时，配电线路含有D个区段，当发生短路故障时，对应的区段状态编码为1，否则编码为0，如式（2）所示。

图2 配电线路区段故障示意图Fig.2 Schematic diagram of faulty section of distribution line

利用智能算法对配电线路进行故障区段定位时，需要构建一个函数将区段状态编码和开关状态编码联系起来，该函数即为开关函数Ij（s），对于单一电源的配电线路，其表达式如下：

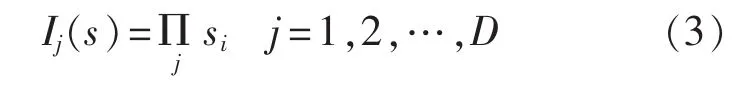
其中，Ij（s）为第 j个开关的开关函数，假设第 j个开关与电源之间的线路称为该开关上游线路，其与线路末端之间的线路称为该开关的下游线路；Π为“逻辑或”运算，表示第j个开关下游线路区段状态至少有1 个为 1 时，Ij（s）就为 1，否则为 0。

式（3）所示的开关函数只适用于单一电源网络，对于并有风电机组等DG的配电线路将会出现误判。另外，配电系统的感性负荷较多，发生故障时负荷继续与配电网连接运行，负荷中心点经大地与配电网主电源的中性点构成回路，因此感性负荷也会对配电线路的故障点产生故障电流［15］。为了解决多电源多重故障且带有感性负荷的配电线路区段定位问题，本文对上述开关函数进行改进，建立新的开关函数如下所示：

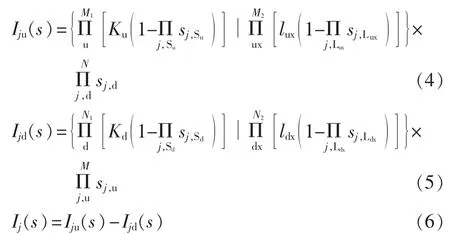
其中，以开关j为分断点，将配电网分成两部分，包含主电源的为上半部分，对应线路为上游线路，其他的为下半部分，对应线路为下游线路，上、下游线路分别有 M1、N1个电源和 M2、N2个负荷；“|”表示“逻辑或”；Iju（s）和 Ijd（s）为第 j个开关上、下游线路的开关函数；Ku、Kd分别为上、下游线路的电源开关系数，若电源接入则取 1，否则取 0；sj，Su、sj，Sd分别为从第 j号开关到上游线路电源、下游线路电源路径上所经过的区段线路状态值；lux、ldx分别为上、下游线路的感性负荷系数，若感性负荷接入则取 1，否则取 0；sj，Lux、sj，Ldx分别为从第j号开关到上游线路感性负荷、下游线路感性负荷路径上所经过的区段线路状态值；sj，u、sj，d分别为上、下游线路所有区段线路状态值；M、N分别为上、下游线路的区段线路总数。

若配电线路中只存在主电源S，存在于第j个开关的上半部分，则开关函数为：

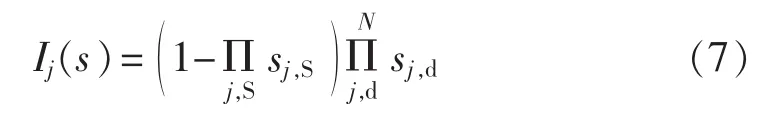
若配电线路中第j个开关上半部分存在主电源S，下半部分存在一个DG S1，此时开关函数变为：

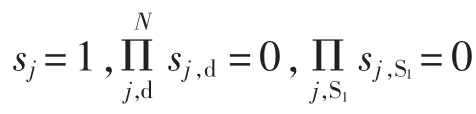
利用所得到的开关状态编码，算法将搜索出所有可能发生故障的区段线路个体解空间，并从中选取最优解，该最优解能最好地解释FTU所上传的开关状态编码。此步骤的关键在于适应度函数的构建，因为适应度值的大小是衡量群体中个体优劣的唯一标准，值越大说明个体性能越好，反之越差。根据开关函数构造出适应度函数如下所示［16］。

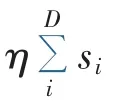
2 基于BPSO算法和GA的二进制混合算法原理

粒子群优化PSO（Particle Swarm Optimization）算法由N个粒子组成群体在D维空间进行寻优搜索。进化过程中粒子根据个体最优位置和群体最优位置不断修正前进方向和速度［16-18］。其中第i个粒子的速度和位置分别为：vi=（vi1，vi2，…，viD），xi=（xi1，xi2，…，xiD）。标准PSO算法按照如下公式进行速度和位置的迭代更新。

其中，ω为惯性权重；学习因子c1和c2分别表示对粒子自身和对整个种群知识的认知，均为正实数；ξ1和ξ2为区间［0，1］上的随机数；分别表示第i个粒子第k次迭代时在第d维的速度和位置；pkbest，d为第i个粒子第k次迭代时在第d维的个体最优位置；gkbest，d表示第k次迭代时在第d维的群体最优位置；i=1，2，…，N；d=1，2，…，D。

BPSO算法则将粒子每一维的状态限制为0或1，速度进化公式保持不变，利用式（12）代替式（11）来实现粒子群算法的二进制化处理。

其中，为［0，1］上的随机数。本文将所有粒子的速度限制在［-4，4］之间，目的在于防止函数饱和。

GA是一种借鉴生物界“优胜劣汰”自然选择过程的随机全局搜索算法。本文首先进行基于线性排序的适应度值分配，按照目标值从小到大的顺序对它们进行排序，并根据排序位置计算出对应个体适应度值，将适应度值大小控制在［0，2］之间，即压差设置为2，计算公式如下：

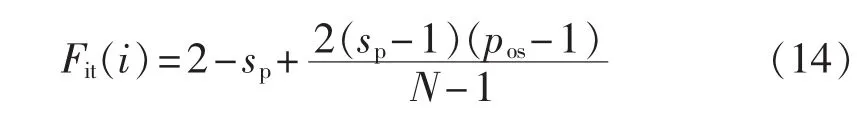
其中，N为种群个体数；pos为个体根据目标值大小在种群中的排序位置；sp为种群中最佳个体选中概率与平均选中概率的比值，它决定了收敛速度，通常取值范围为［1，3］。该排序方法实现了比例适应度计算的均匀尺度变换。

然后进行3个基本操作：选择、交叉和变异。个体被选择的概率由下式给出：

其中，f（xi）为个体 xi的适应度；F（xi）为该个体被选择的概率；N为种群中个体总数。

变异操作是一种局部随机搜索，对于选中的个体以某个变异概率PM改变某一个或者某一些染色体上的基因。

其中，PX为交叉概率；Lind为染色体长度；PM值的选择可以使染色体上的每个基因的变异概率近似等于0.5。以基本位变异算子为例给出下面例子，“ ”表示变异位。

本文中引入了重插入操作。设定重插入因子GGAP，当N个个体经过遗传操作得到NGGAP个个体时，新旧种群的大小差异称为代沟。将旧种群N个个体和新种群NGGAP个个体分别根据适应度值大小排序，并将新种群插入到旧种群中，以代替适应度值较小的NGGAP个父个体。该操作可以进一步保证种群中适应度高的个体进入下一代的进化。

为了使得2种算法形成优势互补，本文提出的基于BPSO算法和GA的BPSOGA故障区段定位方法主要利用双种群进化方式，将群体分成种群规模为N1和N2的2个子种群，并通过信息交换策略使得进化过程中每一代的信息能在2个群体间传递共享，并利用最优信息同步进化。

BPSOGA参数初始化包括：BPSO子种群规模N1、惯性权重 ω、学习因子 c1和 c2、GA 子种群规模 N2、交叉概率 PX、变异概率 PM、重插入因子 GGAP、sp、M、权系数η、最大迭代次数T和种群空间维数D等，取N1=N2=N；随机初始化BPSO子种群中粒子位置p1（i）和粒子速度 vi，并计算粒子适应度值 fit1（i）、粒子最优位置 pbest（i）及粒子最大适应度值 pbest（i）、群体最优位置gpbest及群体最大适应度值gbest；随机初始化GA子种群个体解 p2（i）及个体适应度值 fit2（i）（i=1，2，…，N）；其中 BPSO 子种群中的粒子位置 p1（i）与 GA子种群中个体解p2（i）都采用二进制编码，具有相同的维数，都表征配电线路中对应区段的的区段状态编码。

按照式（10）、（12）和（13）对 BPSO 子种群的粒子速度vi和位置p1（i）进行更新，形成新一代的BPSO种群粒子，并更新适应度值fit1（i）；同时对GA子种群个体适应度值fit2（i）取反，得到目标值，并根据式（14）计算基于线性排序的适应度值 Fit2（i），再进行遗传操作，得到新一代的GA子种群，并更新其适应度值fit2（i）；比较新一代的BPSO子种群的粒子适应度值fit1（i）和对应的新一代的GA子种群的个体适应度值fit2（i），取适应度值大的粒子或个体作为2个种群下一代进化的父代粒子和父代个体：令j=1，进行迭代运算，从而求出最优解。本文提出的BPSOGA流程图如图3所示。

图3 所提算法流程图Fig.3 Flowchart of proposed algorithm

3 仿真算例分析

本文采用如图4所示的含有风电机组的配电线路模型。其中，S为系统主电源，K1—K3为风电机组并入配电线路的开关，L1、L2为感性负荷。案例中设置了30个开关，如图中黑色圆点所示，编号为1—30，同时设置 30 条区段线路，编号为（1）—（30），具体位置如图4所示。区段定位开始时对程序进行参数初始化：BPSO种群个体总数N1=50，惯性权重ω=0.9，学习因子c1=c2=1.5，GA种群个体总数N2=50，交叉概率PX=0.7，变异概率PM=0.2／30，重插入因子GGAP=0.9，最大迭代次数T=100，种群空间维数D=30，M=60，sp=2，η=0.5。 仿真中，BPSOGA 维数与开关个数、区段线路总数都相同，以维数状态值表示区段状态编码值。

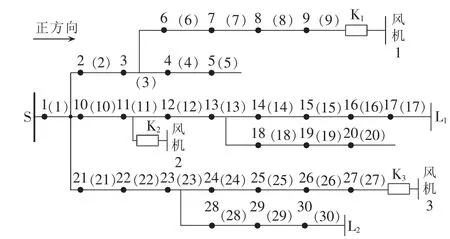
图4 配电线路示意图Fig.4 Schematic diagram of distribution lines

首先，本文设置区段（3）发生单相接地故障，所有的风电机组并网运行，FTU反馈结果为［1 1 1 0 0-1-1-1-1-1-1-1-1-1-1-1-1 0 0 0-1-1-1-1-1-1-1-1-1-1］，将其输入本文提出的BPSOGA中，启动算法可得到如图5所示个体适应度分布图和图6所示维数状态值图。

由图5可知，当区段（3）发生单相接地故障时，个体的适应度值最大为59.5，对应的个体编号为28，由图6可知第28个个体的维数状态值为［001000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0］，第 3 维的编码为1，可得知对应的区段（3）发生故障，定位结果与预先设置的故障情况相吻合。

图5 个体适应度值分布图Fig.5 Schematic diagram of individual fitness distribution

图6 维数状态值图Fig.6 Diagram of dimension status value

配电线路往往会发生多重故障，DG投入位置和数量不固定，且FTU上传的信息受外界环境影响会发生畸变。为了检验BPSOGA故障区段定位的准确性、有效性和容错性，下面对图4所示的算例在不同的情况下进行仿真分析。 其中［B1，B2，B3］表示风电机组的开关系数矩阵，当 Bi=1（i=1，2，3）时，表示对应的风电机组并入配电线路，否则表示不并入配电线路。感性负载始终接入线路中。

a.单一故障。

当线路发生单一故障，风电机组数量不同，并网位置不同，且FTU上传的信息发生畸变时，仿真结果如表1所示，对于同一故障，无论风电机组的并网位置改变与否、数量改变与否、故障信息畸变与否，该算法都能准确定位，说明本文算法适应于不同情况下的单一故障区段定位。

b.两重故障。

设置与单一故障相同的条件，仿真两重故障，结果如表2所示，可知算法适应于不同情况下的两重故障。

c.三重故障。

设置与单一故障、两重故障相同的条件，仿真三重故障，结果如表3所示，可知算法适应于不同情况下的三重故障。

由以上仿真结果可以看出，BPSOGA适用于发生单一、两重、三重等多重故障（限于篇幅，不再详细说明）的区段定位，且当风电机组并入配电线路的位置、数量发生变化时，该算法都能准确地确定出故障区段，具有较高的准确性。即使在FTU上传的个别故障信息畸变时，算法也能准确完成故障区段定位，具有一定的容错性。

表1 单一故障仿真结果Table 1 Simulative results of single fault

表2 两重故障仿真结果Table 2 Simulative results of double faults

此外，本文从出现“未成熟收敛”现象和收敛速度两方面比较改进后的BPSOGA在配电线路定位时与BPSO算法和GA的性能。

分别利用3种算法对预设的同一个单一故障进行定位分析，每种算法连续运行30次，再预设两重、三重故障，操作方法与单一故障时相同，得到的3种算法出现“未成熟收敛”次数比较结果如表4所示。

表3 三重故障仿真结果Table 3 Simulative results of triple faults

表4 3种算法出现“未成熟收敛”的次数Table 4 Times of premature convergence for three algorithms

由表4可以看出，单独使用BPSO算法或GA进行故障区段定位时，均出现了“未成熟收敛”现象，且次数随着故障重数的增加而增加；而使用改进后的BPSOGA后，未出现该现象。

同一故障下3种算法的收敛速度如图7所示，可明显看出改进后的BPSOGA比单独使用其余2种算法的收敛速度快，更容易得出全局最优解，避免不必要的冗余迭代。这两方面充分说明改进后的算法性能得到提升。

图7 3种算法的收敛速度比较Fig.7 Comparison of convergence speed among three algorithms

4 结论

风电机组等DG并入配电线路会改变其结构和潮流分布，这给配电线路的故障定位带来新的挑战。本文提出统一假定配电线路的网络正方向，以网络正方向为基础假定每个开关的上下半部分和上下游线路。对开关函数和适应性函数进行改进，充分利用FTU上传的故障信息进行区段定位。同时本文提出了一种基于BPSO算法和GA的二进制混合算法，对含风电机组的配电线路进行故障区段定位，将区段定位问题转变为一个利用算法求解适应度函数最大值的最优解问题。该算法利用双种群进化机制，在进化过程中2个子种群互不干扰，在完成每一代的进化后共享最优个体，进行信息交换传递，使BPSO算法和GA在进化过程中相互监督，帮助对方跳出“未成熟收敛”。仿真结果表明，BPSOGA适应于单一和多重故障，对DG并入配电线路的数量和位置没有限制，且具有一定的容错性，对于畸变信息依旧能准确定位出故障区段。相比于单独使用BPSO算法和GA，收敛速度得到提高，出现“未成熟收敛”的概率降低。

［1］钱科军，袁越，石晓丹，等．分布式发电的环境效益分析［J］．中国电机工程学报，2008，28（29）：11-15．QIAN Kejun，YUAN Yue，SHI Xiaodan，et al. Analysis of environmental benefit of distributed generation［J］.Proceedings of the CSEE，2008，28（29）：11-15.

［2］OCHOA L F，PADIHA-FELTRINA A，HARRISON G P.Evaluating distributed generation impacts with a multi objective index［J］.IEEE Transactions on Power Delivery，2006，21（3）：1452-1458.

［3］麻秀范，崔换君．改进遗传算法在含分布式电源的配电网规划中的应用［J］．电工技术学报，2011，26（3）：175-181．MA Xiufan，CUI Huanjun.An improved genetic algorithm for distribution network planning with distributed generation［J］.Transactions of China Electrotechnical Society，2011，26（3）：175-181.

［4］孙景钌，陈荣柱，蔡轼，等．含分布式电源配电网的故障定位新方案［J］．电网技术，2013，37（6）：1645-1650．SUN Jingliao，CHEN Rongzhu，CAI Shi，et al.A new fault location scheme for distribution system with distributed generations［J］.Power System Technology，2013，37（6）：1645-1650.

［5］康龙云，郭红霞，吴捷，等．分布式电源及其接入电力系统时若干研究课题综述［J］．电网技术，2010，34（11）：43-47．KANG Longyun，GUO Hongxia，WU Jie，et al.Characteristics of distributed generation system and related research issues caused by connecting it to power system［J］.Power System Technology，2010，34（11）：43-47．

［6］孙鸣，余娟，邓博．分布式发电对配电网线路保护影响的分析［J］．电网技术，2009，33（8）：104-107．SUN Ming，YU Juan，DENG Bo．Analysis of impact of DGs on line protection of distribution networks［J］.Power System Technology，2009，33（8）：104-107.

［7］刘蓓，王沨，陈春，等．和声算法在含DG配电网故障定位中的应用［J］．电工技术学报，2013，28（5）：280-284．LIU Bei，WANG Feng，CHEN Chu n，et al.Harmony search algorithm for solving fault location in distribution networks with DG［J］.Transactions of China Electrotechnical Society，2013，28（5）：280-284.

［8］王江海，邰能灵，宋凯，等．考虑继电保护动作的分布式电源在配电网中的准入容量研究［J］．中国电机工程学报，2010，30（22）：37-43．WANG Jianghai，TAI Nengling，SONG Kai，et al.Penetration level permission of for DG in distributed network considering relay protection［J］.Proceedings of the CSEE，2010，30（22）：37-43.

［9］THUKARAM D，KHINCHA H P，VIJAYNARASIMHA H P.Artificial neural network and support vector machine approach for locating faults in radial distribution systems［J］.IEEE Transactions on Power Delivery，2005，20（2）：710-721.

［10］刘健，张志华，张小庆，等．配电网模式化故障处理方法研究［J］．电网技术，2011，35（11）：253-257．LIU Jian，ZHANG Zhihua，ZHANG Xiaoqing，et al.Modeled fault isolation and restoration for distribution systems［J］.Power System Technology，2011，35（11）：253-257.

［11］王进强．含分布式电源的配电网故障定位的应用研究［D］．广州：广东工业大学，2011．WANG Jinqiang.Application study of fault location for distribution network containing distributed generation［D］.Guangzhou：Guangdong University of Technology，2011.

［12］刘健，张小庆，同向前，等．含分布式电源配电网的故障定位［J］．电力系统自动化，2013，37（2）：36-48．LIU Jian，ZHANG Xiaoqing，TONG Xiangqian，et al.Fault location for distribution systems with distribution generations［J］.Automation of Electric Power Systems，2013，37（2）：36-48.

［13］郑顾平，姜超，李刚，等．配网自动化系统中小电流接地故障区段定位方法［J］．中国电机工程学报，2012，32（13）：103-109．ZHENG Guping，JIANG Chao，LI Gang，et al.Method of fault area& section location for non-solidly earthed distribution system［J］.Proceedings of the CSEE，2012，32（13）：103-109.

［14］郭壮志，吴杰康．配电网故障区间定位的仿电磁学算法［J］．中国电机工程学报，2010，30（13）：34-40．GUO Zhuangzhi，WU Jiekang.Electromagnetism-like mechanism based fault section diagnosis for distribution network［J］.Proceedings of the CSEE，2010，30（13）：34-40.

［15］梁睿，靳征，王崇林，等．行波时频复合分析的配电网故障定位研究［J］．中国电机工程学报，2013，33（28）：130-136.LIANG Rui，JIN Zheng，WANG Chonglin，et al.Research of fault location in distribution networks based on integration of travelling wave time and frequency analysis［J］.Proceedings of the CSEE，2013，33（28）：130-136.

［16］李振坤，陈星莺，余昆，等．配电网重构的混合粒子群算法［J］．中国电机工程学报，2008，28（31）：36-41．LI Zhenkun，CHEN Xingying，YU Kun，et al.Hybrid particle swarm optimization for distribution network reconfiguration ［J］.Proceedings of the CSEE，2008，28（31）：36-41.

［17］吴小刚，刘宗歧，田立亭，等．基于改进多目标粒子群算法的配电网储能选址定容［J］．电网技术，2014，38（12）：3405-3411．WU Xiaogang，LIU Zongqi，TIAN Liting，et al.Energy storage device locating and sizing for distribution network based on improved multi-objective particle swarm optimizer［J］.Power System Technology，2014，38（12）：3405-3411.

［18］李超文，何正友，张海平，等．基于二进制粒子群算法的辐射状配电网故障定位［J］．电力系统保护与控制，2009，37（7）：35-39．LI Chaowen，HE Zhengyou，ZHANG Haiping，et al. Fault location for radialized distribution networks based on BPSO algorithm［J］.Power System Protection and Control，2009，37（7）：35-39.