一种含间隙解耦并联机构动力学分析与混沌现象辨识

侯雨雷， 张占叶， 李明洋， 汪　毅， 曾达幸， 李慧剑(.燕山大学 机械工程学院，河北 秦皇岛　066004；. 燕山大学 河北省重型装备与大型结构力学可靠性重点实验室，河北 秦皇岛　066004)



一种含间隙解耦并联机构动力学分析与混沌现象辨识

侯雨雷1， 张占叶1， 李明洋1， 汪毅1， 曾达幸1， 李慧剑2(1.燕山大学 机械工程学院，河北 秦皇岛066004；2. 燕山大学 河北省重型装备与大型结构力学可靠性重点实验室，河北 秦皇岛066004)

摘要：以自主提出的一种两转动解耦并联机构为研究对象，阐述机构结构组成，并针对其运动副存在间隙状况，建立含间隙机构动力学模型；基于ADAMS软件进行动力学仿真，并分析在有无运动副间隙、不同间隙和驱动速度下，机构位移、速度、加速度以及运动副接触力的变化；借助Poincare截面映射法对解耦并联机构动力学行为中的混沌现象予以辨识，绘制Poincare映射图，揭示间隙对机构动力学特性的影响。研究结果表明含间隙解耦并联机构存在混沌运动现象，对其更进一步的非线性动力学研究有一定指导意义。

关键词：解耦并联机构；间隙；动力学；混沌辨识

在实际机械系统中，运动副间隙是不可避免的，由于间隙的存在，使得机构的动力学系统为非线性系统，而混沌现象普遍存在于非线性系统中[1]，研究机构动力学混沌现象可以更好的揭示系统宏观动力学特性。

混沌是确定的非线性动力系统所特有的复杂运动形态。混沌打破了确定性与随机性之间不可逾越的分界线，初始条件的微小变化将导致系统运动状态的巨大差异[2]。由于混沌在工程技术上的重大研究价值和极其诱人的应用前景，混沌理论及其应用已成为非线性科学研究的一个热点[3-4]。James等[5]分析了直升机振动机制，探讨了直升机振动中混沌行为存在的可能性及其对动力系统的影响。Zukovic等[6]分析了一种含间隙的非理想机械系统中的混沌现象，通过求解最大Lyapunov指数证明了系统中混沌的存在，并发现系统经倍周期分岔而进入混沌。

迄今为止，机构学中混沌现象的研究大多集中在机构动力学分析方面，尤其是带间隙的运动副和有柔性构件的连杆机构、非线性齿轮传动力和齿侧间隙引起的非线性动力学分析等。金国光等[7]依据变胞机构全构态动力学模型，研究了双柔性机械臂动力学中的混沌现象。李立等[8]通过分析混沌的数值方法，获得平面串联型运动冗余机器人自运动状态与其零空间中矢量关系的统计规律。王国庆等[9]采用非线性弹簧阻尼模型分析了含间隙机构的非线性，证明了其运动中存在混沌现象。王三民等[10]分析了弧齿锥齿轮的非线性特性，得出随支撑刚度变化弧齿锥齿轮系经拟周期分岔进入混沌振动。陈学森等[11]针对含间隙非线性单级齿轮系统，利用OGY混沌控制原理，通过对外激励参数实施连续的小扰动，将系统的混沌吸引子内的不稳定周期轨道稳定化。马洪涛等[12]分析了行星换向机构的分岔及混沌特性，通过增大转速使系统由周期运动状态统突变为混沌状态，又通过增大扭矩使系统由混沌状态转为单周期运动状态。谢进等[13]分析了驱动关节运动已知的平面2R欠驱动机械臂混沌运动，当机构受重力作用且驱动关节运动频率较高时，机构将呈现混沌运动状态。

混沌识别是研究混沌的前提和首要条件。准确而高效的对系统混沌进行辨识是实现混沌控制、利用的基础。由于混沌运动具有复杂性和非周期性的特点，关于混沌理论的研究还处于探索阶段，主要通过求解非线性系统动力学微分方程数值解，分析数值解在时域、空间等的特征来判断系统是否处于混沌状态。应用较广泛的数值分析方法有：时间历程和相图法、庞加莱(Poincare)截面法、自功率谱密度分析法、分维数分析法以及最大李雅普诺夫(Lyapunov)指数法[14]等。

现有文献中，机构的动力学及混沌现象分析已较普遍，而针对解耦并联机构混沌现象的分析鲜有报道。相比其他机构而言，并联机构运动输出为各分支不同运动副共同作用结果，而对应某一特定任务，机构各运动副多为往复、交变运动，并非单一方向的运转，在此情况下建立并联机构合理的间隙副模型，分析运动副间隙对机械系统动力学特性的影响对机构的设计及应用具有重要的工程实际意义。

本文将以含间隙RU-RPR(R为转动副，U为虎克铰，P为移动副)解耦并联机构为研究对象，建立机构动力学仿真模型，以并联机构学和混沌理论为基础，借助ADAMS软件分析机构在不同间隙大小、不同工况下的动力学行为及相关特性，并对机构混沌现象予以辨识。

1解耦并联机构动力学仿真建模的建立

1.1并联机构结构组成

如图1所示为RU-RPR并联机构简图，该并联机构具有两转动自由度[15]，可用于追踪飞行目标，如天线座等。RU-RPR并联机构由定平台、动平台以及连接两平台的两条支链组成，从定平台到动平台，第一条分支链依次由转动副(R)和虎克铰(U)相连，第二条分支链依次由转动副、移动副(P)和转动副相连。其中，第二条分支中移动副的移动方向垂直于该分支两个转动副的轴线，两分支中与固定平台相连的两转动副轴线相互平行且与虎克铰的一条轴线平行，虎克铰的另一条轴线与第二分支中与动平台相连的转动副轴线重合。

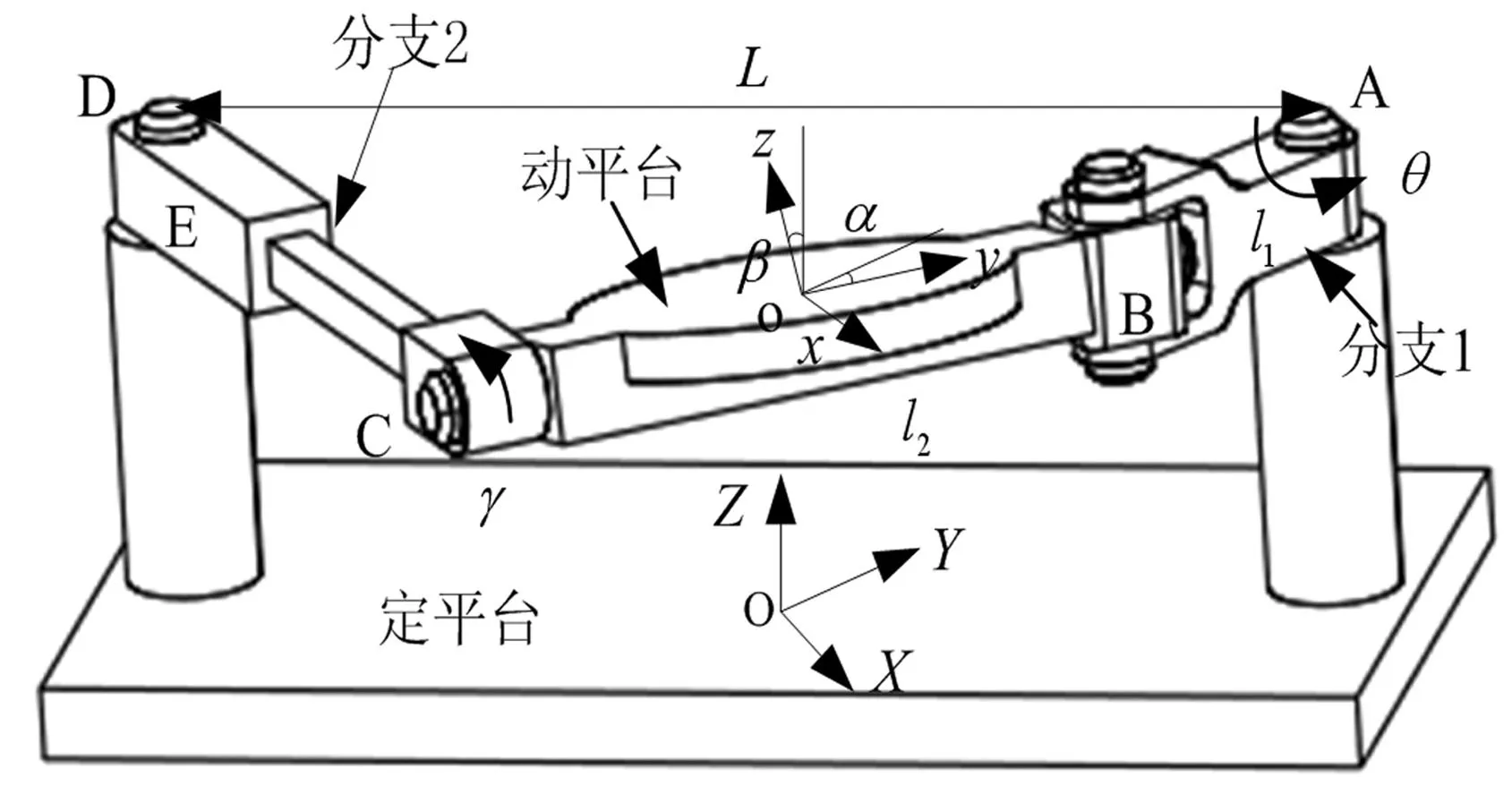
图1　RU-RPR 2自由度转动并联机构Fig.1 RU-RPR 2-DOF rotational parallel mechanism

在定平台上固连定坐标系O-XYZ，其中，坐标原点O为与连线中点在定平台平面的投影，Z轴竖直向上，Y轴与和定平台相连的两转动副A、D轴线垂直并指向A；在动平台上固连动坐标系o-xyz，其中，坐标原点o建立在动平台几何中心，y轴和分支2中与动平台相连的转动副的轴线共线，方向指向虎克铰，z轴与动平台平面垂直，方向向上。

1.2解耦并联机构运动学分析

如图1所示，将RU-RPR并联机构第一分支的转动副和第二分支与动平台相连的转动副作为主动副。符号定义如下：以θ表示第一分支的转动副绕Z轴旋转角度；γ表示第二分支与动平台相连的转动副绕Y轴旋转角度；α和β分别表示动平台绕动坐标系的z轴和y旋转角度；L表示与固定平台相连的两个转动副轴线间的垂直距离，l1和l2分别表示杆AB、BC的长度。根据机构位置与速度分析，可得其雅可比矩阵为[16]

(1)

RU-RPR并联机构具有绕y轴和z轴的两转动自由度[15]，且其雅可比矩阵J为对角阵，故该机构为完全解耦，即两转动互不影响。因此，在研究转动副D处的间隙时，可暂不考虑机构绕y轴的转动，而只考虑动平台沿z轴(铅垂方向)的转动，故可将RU-RPR解耦并联机构视作一个平面四杆机构，其等效机构简图如图2所示。

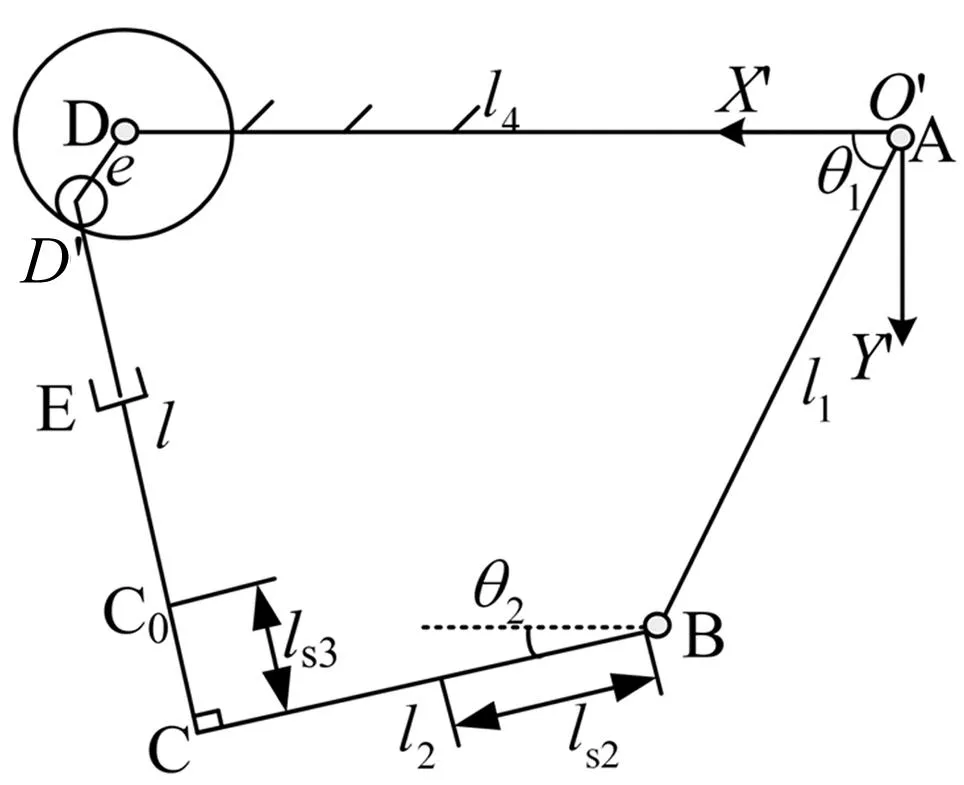
图2　含间隙两转动并联机构等效机构简图Fig.2 Schematic diagram of the equivalent mechanism of two rotation parallel mechanism with clearance

1.3机构动力学仿真模型的建立

针对等效的含间隙RU-RPR解耦并联机构建立平面坐标系X′O′Y′，并对后续动力学分析所需相关参数定义如下：l1、θ1、J1分别表示杆AB的长度、转角以及对转动连接副A的转动惯量；l2、ls2、θ2、m2、Js2分别表示杆BC的长度、质心S0距运动副B的距离、转角(与X′轴正向的夹角)、质量以及对自身质心的转动惯量；m3、ls3、Js3分别表示杆CE的质量、质心C0与C之间的距离以及对自身质心的转动惯量；l表示CD之间的距离，l4表示机架的长度；x、y分别表示间隙(图中小圆表示轴销，大圆表示轴套)的横向、纵向分量，即轴销和轴套间的横向、纵向相对位移分量。

机构杆件形状如图1所示，多选用长方形和圆柱形，其材料为45钢，则可得到RU-RPR机构相关参数如下：l1=130 mm，l2=308 mm，ls2=0.154 mm，ls3=79.7 mm，l4=520 mm，J1=7.351×10-3kg·m2，Js2=6.16×10-2kg·m2，Js3=5.772×10-3kg·m2,J4=7.105×10-3kg·m2，m2=8.516 kg，m3=1.161 kg。

应用软件对机构建模时，默认运动副都是理想约束，而在实际机构中，因设计时动配合的考虑以及加工装配中的误差，运动副之间存在间隙，进而导致运动过程中的冲击和碰撞。为真实的反映现实中含间隙的运动副之间的碰撞情况，利用ProE软件建立RU-RPR解耦并联机构三维实体模型并设置间隙，之后导入ADAMS中，根据含间隙运动副的作用机理，结合软件提供的约束联合建立等效间隙约束。

将运动副之间的碰撞模型等效为弹簧阻尼模型，采用冲击函数法计算碰撞力，即通过Impact函数计算两构件之间的接触力，该接触力由两部分组成：① 两构件之间相互切入，表面发生细微变形而会产生相互作用的弹性力；② 由于相对速度的存在，产生阻尼力。弹簧接触力根据Hertz接触理论来计算，同时用阻尼器模拟接触过程中的能量损失。

本文采用Gstiff积分器中的SI2积分格式进行求解，对非连续问题，SI2积分格式求解速度稍慢，但是稳定性较好。设置ADAMS中机构间隙模型建立所涉及的各项参数如表1所示。

表1　RU-RPR解耦并联机构间隙模型碰撞参数

2解耦并联机构动力学仿真分析

将D处转动副含间隙RU-RPR机构和不含间隙RU-RPR机构的三维模型分别导入到ADAMS中。在不考虑含间隙时，D处将添加理想的转动副约束；当D转动副处有间隙时，对其施加接触力约束。如下分别分析有无转动副轴销与轴套间的径向间隙、径向间隙不同、驱动速度不同时机构的动态性能。

2.1有无间隙机构动力学性能分析

设转动副D处轴销与轴套间的径向间隙为0.3 mm，驱动角速度为ω=12π rad/s，模拟运行的时间选取为0.5 s，即运转3个周期。RU-RPR解耦并联机构在无间隙理想状态与D转动副处含间隙时，动平台质心在定坐标系中的位移、速度变化曲线分别如图3、图4所示。鉴于含间隙机构初始碰撞时，碰撞深度较大，接触力也较大，对机构动态特性影响也较剧烈，故在图4中采用局部放大的方式以观察机构在初始碰撞时速度曲线的变化过程，从而在一定程度上便于认识到间隙对机构动态特性的影响。文中后续其它图中放大图的作用类似，不再一一赘述。

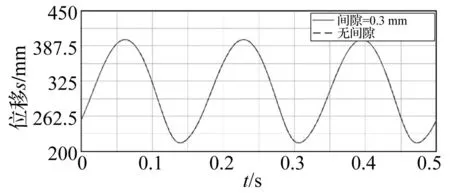
图3　考虑间隙与无间隙机构动平台位移变化曲线对比图Fig.3 Comparison diagram of displacement variation for the moving platform of the mechanism considering clearance or not

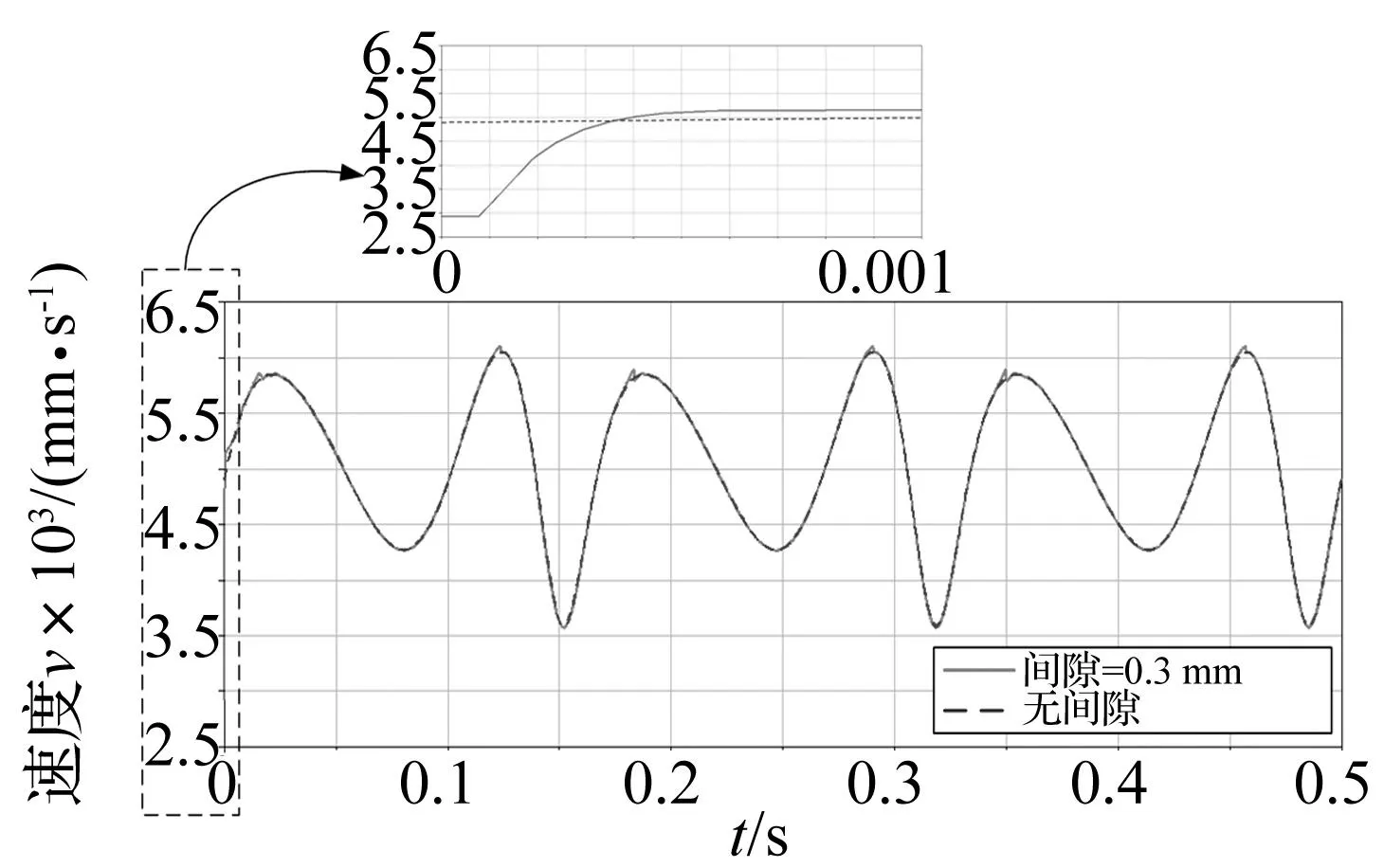
图4　考虑间隙与无间隙机构动平台速度变化曲线对比图Fig.4 Comparison diagram of the velocity variation for the moving platform of the mechanism considering clearance or not

由图3可知，含间隙与无间隙理想机构的位移曲线图基本重合，位移稳定变化，说明间隙对机构动平台位移的影响是很小的。

如图4所示，含间隙机构运动初始阶段，动平台质心发生较大的速度变化，由此推断，含间隙机构在运动之初，轴销和轴套处于分离状态，施加驱动后使得轴销和轴套发生猛烈的冲击，因此出现角速度突变，但由于接触摩擦和阻尼作用，动平台又很快稳定下来，逐步进入平稳状态，后续中含间隙与无间隙机构速度曲线基本重合，说明间隙对机构动平台速度的影响比较小。

图5～图7分别为考虑间隙与无间隙时，机构动平台质心加速度和角加速度以及轴销轴套接触力变化曲线。

图5　考虑间隙与无间隙时机构动平台加速度变化曲线对比图Fig. 5 Comparison diagram of the acceleration variation for the moving platform of the mechanism considering clearance or not

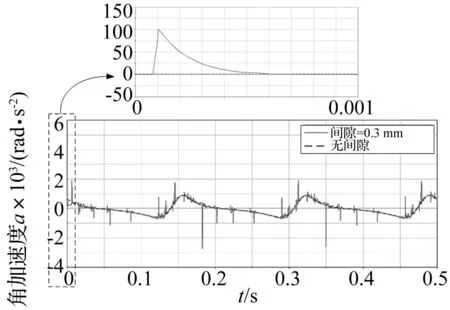
图6　考虑间隙与无间隙时机构动平台角加速度变化曲线对比图Fig.6 Comparison diagram of the angular acceleration variation for the moving platform of the mechanism considering clearance or not

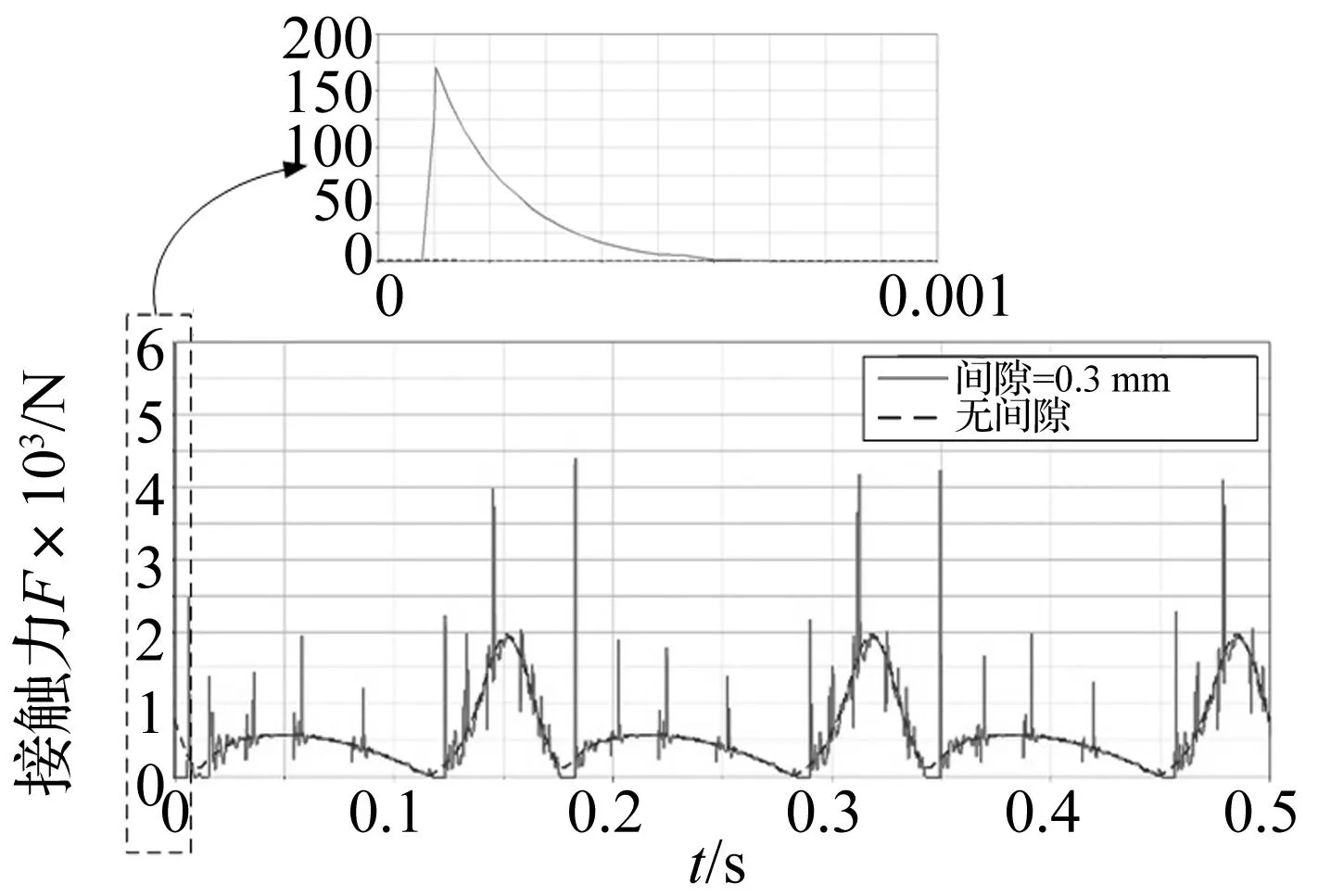
图7　考虑间隙与无间隙时机构D处轴销轴套接触力变化曲线对比图Fig.7 Comparison diagram of contact force for the shaft pin and sleeve on D point of the mechanism considering clearance or not

通过对图5～图7变化曲线对比分析可知，无间隙理想机构动平台的加速度、角加速度以及轴销与轴套之间接触力的曲线变化平稳，没有突变；而考虑间隙机构动平台的加速度、角加速度和轴销轴套之间的接触力曲线突变明显，运动不稳定，尤其是在运动初始阶段，轴销和轴套发生冲击，使铰关节瞬间产生一个很大的接触力，并引起较大的初始加速度和角加速度，说明间隙对机构的加速度和角加速度影响比较显著。

从接触力变化曲线图上可以看出，含间隙机构在运动初始的两个周期内，出现了多个接触力的峰值，分别为运动起始时的170 470 N和各个周期内的4 391 N、4 183 N、4 099 N等，由此可见，含有间隙时，不仅在起始时接触力会突然变大，在每个运动周期也会出现偏离理想状态数值的高次波，因此，在机构设计和制造时，需要考虑间隙对轴套轴销接触力的影响，在长期、往复作用情况下，接触力变化对运动副疲劳磨损的影响不可忽视。

从图4～图7中的放大图可以看出，在运动起始时，轴销与轴套未接触时，接触力为0，速度、加速度以及角加速度曲线变化比较平稳；而当轴销与轴套初始接触时，接触力迅速增大，与此同时，速度、加速度、角加速度曲线也显著变化。对比接触力的放大图与原图可以看出，初始运行时的接触力峰值是运动过程中峰值的几十倍，这是由于初始运行时，存在较大的冲击所造成，因而不能忽略初始运行的影响。

综合以上分析可知，由于间隙的存在，轴销和轴套产生碰撞，对机构的运动性能，即位移和速度的影响较小，而对机构的动态特性，包括加速度、角加速度以及接触力有较大的影响。

2.2径向间隙不同时机构动力学性能分析

当驱动角速度为ω=12π rad/s时，改变轴销和轴套之间径向间隙的大小，进行机构的动力学仿真。

如图8所示为径向间隙分别为0.05 mm和0.5 mm时动平台质心加速度对比曲线。两种径向间隙下，径向间隙为0.05 mm时初始加速度为1.419×107mm/s2，径向间隙为0.5 mm时初始加速度为1.369×107mm/s2，二者基本相同。同时由放大图可以看出，径向间隙为0.05 mm时，加速度曲线变化更迅速，这是因为间隙较小时，轴销与轴套初始接触所需要的时间更短。而在运动过程中，径向间隙为0.05 mm时的加速度曲线与径向间隙为0.5 mm时的加速度曲线相比，径向间隙为0.5 mm时存在更多的波峰，波动更加剧烈。这与角加速度曲线以及接触力曲线是一致的，如图9，图10所示。

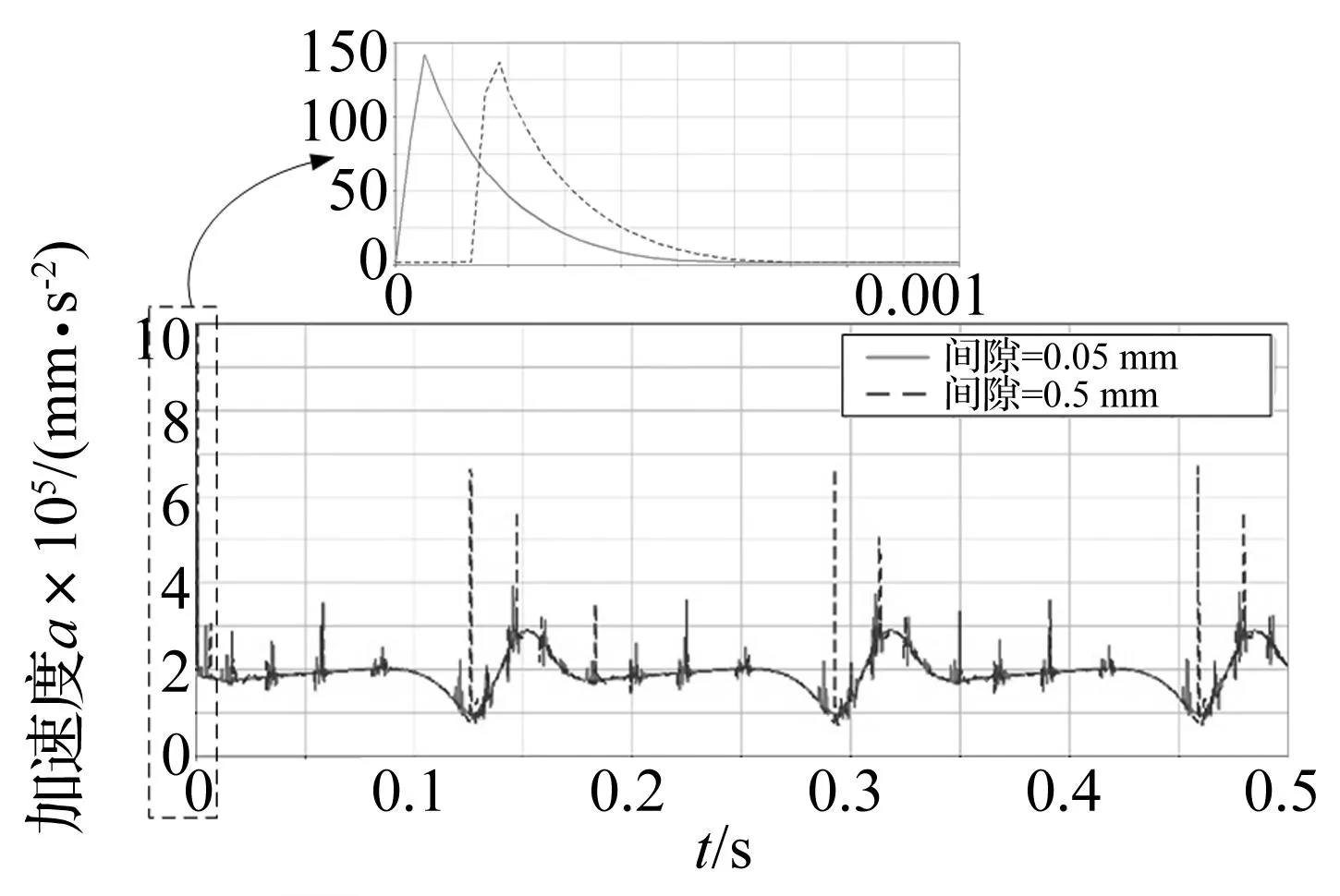
图8　不同径向间隙下机构动平台质心加速度变化曲线对比图Fig.8 Comparison diagram the acceleration variation for the moving platform of the mechanism under different radial clearance

图9　不同径向间隙下机构动平台质心角加速度变化曲线对比Fig.9 Comparison diagram of the angular acceleration variation for the moving platform of the mechanism under different radial clearance

图10　不同径向间隙时D处轴销轴套接触力变化曲线对比图Fig.10 Comparison diagram of the contact force variation for the shaft pin and sleeve on D point under different radial clearance

通过对图8～图10的分析可知，随着间隙的增大，曲线的波动幅值比较大，说明间隙越大，铰关节处冲击碰撞严重，将导致机构运动更加不稳定，产生较大的波动。

可见，间隙的变化会对机构的动态特性造成较大的影响，从这一角度出发，结构设计过程中，在零件选材、精度要求等方面要有针对性考虑。

2.3驱动速度不同时机构动力学性能分析

当转动副D处的径向间隙为0.3 mm，驱动角速度分别为12π rad/s和30π rad/s时，对含间隙解耦并联机构进行动力学仿真。动平台质心速度、加速度以及接触力曲线分别如图11～图14所示。

图11　驱动角速度不同时含间隙机构动平台质心速度变化曲线Fig.11 Velocity variation curve for the moving platform of the mechanism under different driving angular velocities

图12　驱动角速度不同时含间隙机构动平台质心加速度变化曲线Fig.12 Acceleration variation curve for the moving platform of the mechanism under different driving angular velocities

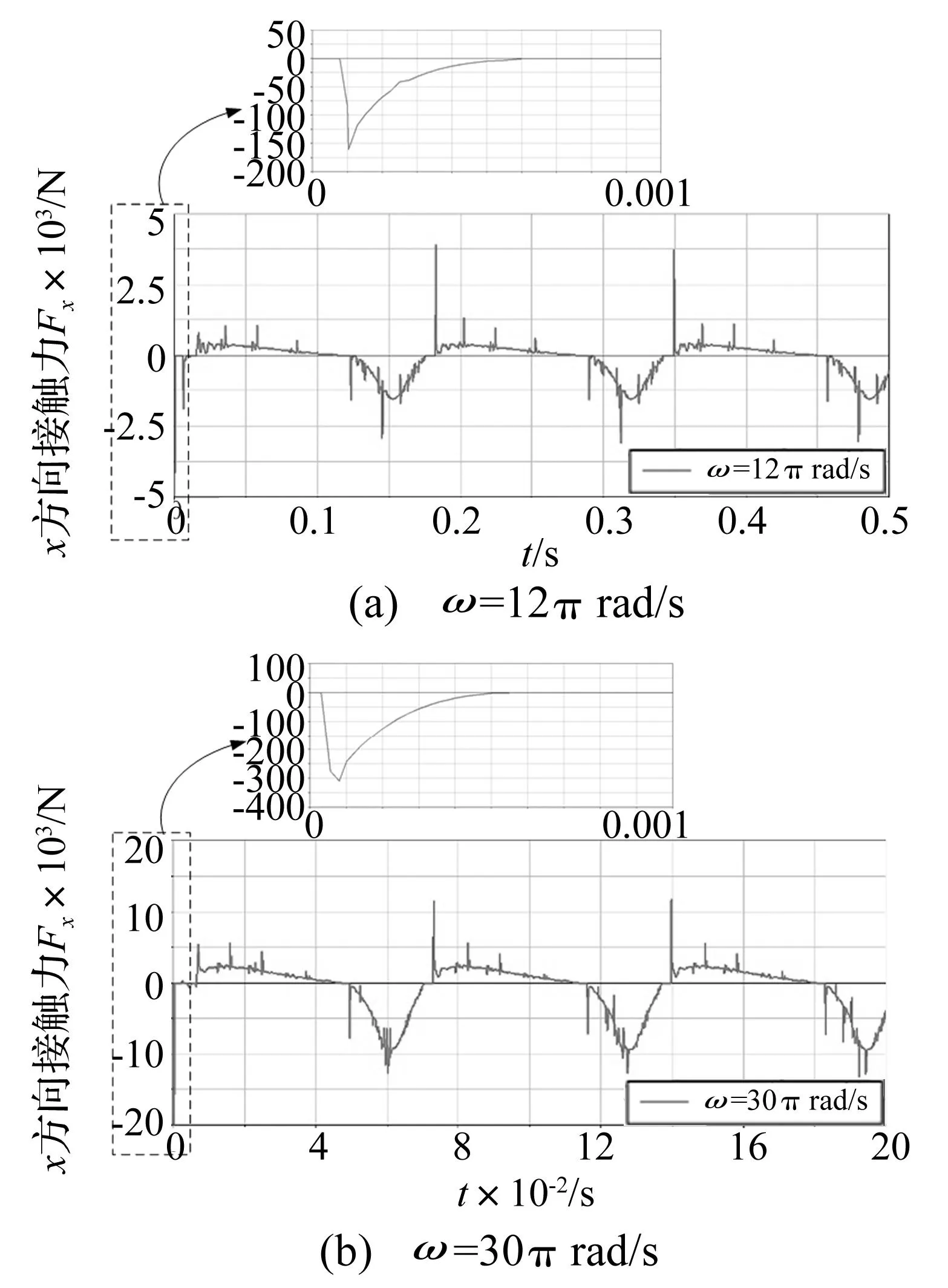
图13　驱动角速度不同时含间隙机构销轴与轴套间接触力在x方向分量变化曲线Fig.13 Contact force component along x direction variation curve for the shaft pin and sleeve on D point under different driving angular velocities

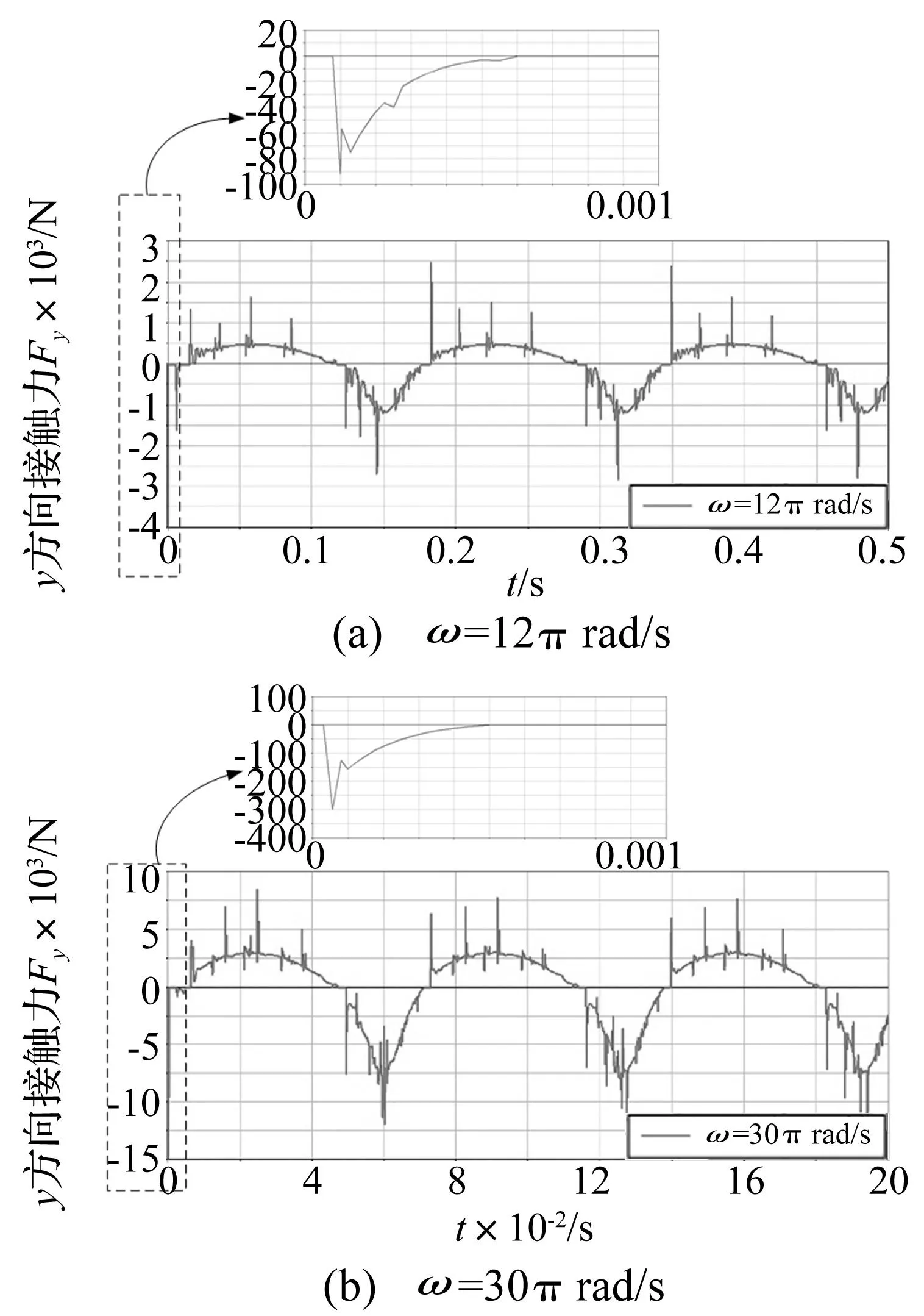
图14　驱动角速度不同时含间隙机构销轴与轴套间接触力在y方向分量变化曲线Fig.14 Contact force component along y direction variation curve for the shaft pin and sleeve on D point under different driving angular velocities

从图11可以看出，解耦并联机构动平台质心速度变化曲线比较光滑，说明驱动角速度的变化对动平台质心速度无明显的影响。图12表明，驱动角速度的变化对动平台质心加速度有显著影响，驱动角速度越小，动平台的质心加速度振动频率越大，运动表现不稳定；而当驱动角速度较大时，动平台加速度相比而言变得稳定，运动曲线相对光滑理想，表明在某一特定的间隙条件下，增大驱动角速度对机构动态特性是有利的。

由图13、图14可以看出在ω=30π rad/s时，销轴和轴套间接触力的曲线变化相比ω=12π rad/s时的曲线较为光滑，表明驱动角速度的变化会明显影响销轴与轴套间接触力，即在一定的间隙条件下，增大驱动角速度使得机构的动态特性相对比较稳定。

3含间隙解耦并联机构混沌现象辨识

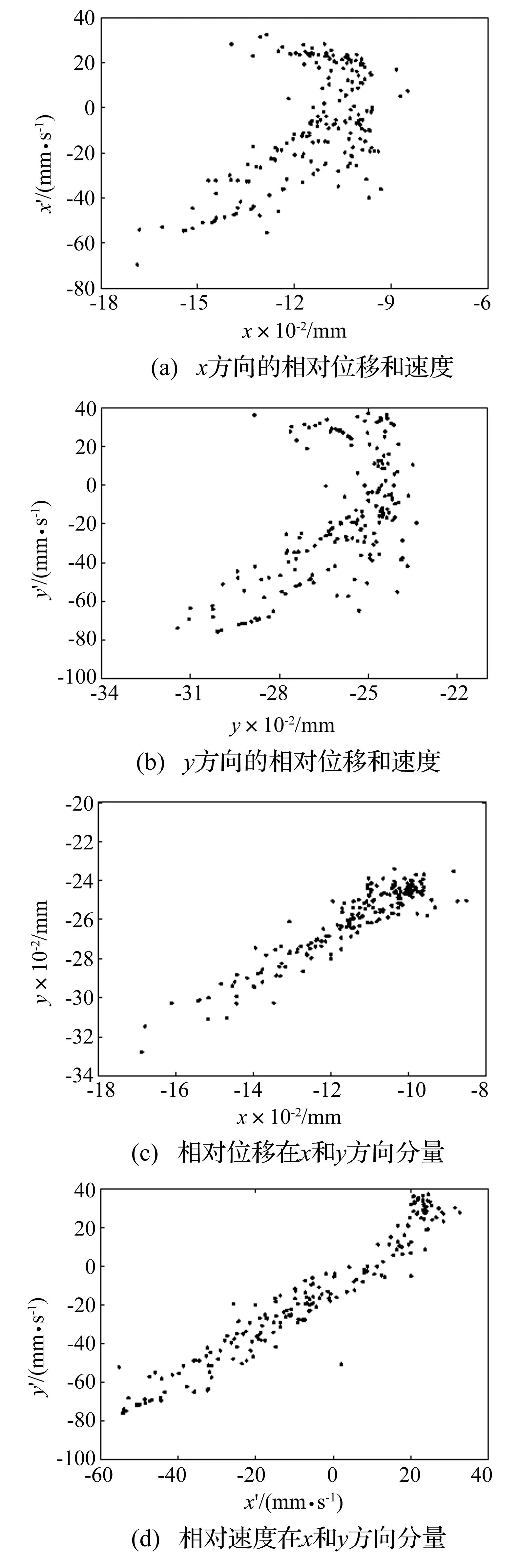
图15　径向间隙为0.3 mm时解耦并联机构Poincare映射图Fig.15 Poincare maps of the decoupled parallel mechanism under radial clearance of 0.3 mm

通过图15所示的Poincare映射图可以看出，在Poincare截面上，大量的映射点呈现带状分布而非孤立点或闭合曲线，并且相邻的映射点之间没有关系，由此可以判断此时RU-RPR解耦并联机构处于混沌状态，并且当系统处于混沌时，映射点数的多少并不会改变映射形状，只是大量的映射点将使映射的形状更为稠密[17]。

改变径向间隙的大小，取r=0.05 mm，与前述类似作RU-RPR解耦并联机构Poincare映射图，其形状如图16所示。

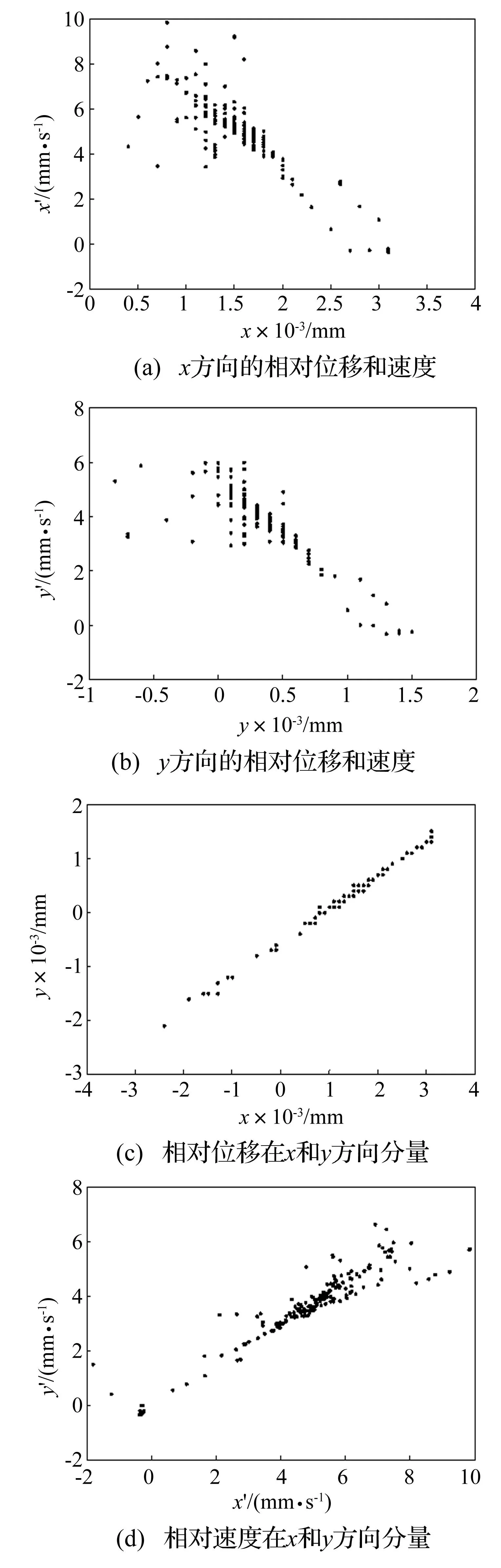
图16　径向间隙为0.05 mm时解耦并联机构Poincare映射图Fig.16 Poincare maps of the decoupled parallel mechanism under radial clearance of 0.05 mm

通过对比分析图15和图16可以看出，随着运动副间隙值的减小，机构Poincare映射点向直线趋势收缩，说明RU-RPR解耦并联机构混沌现象有所减轻；考虑极限或理想情况，当运动副无间隙时，Poincare截面上将只有一个点，此时机构没有混沌现象。

4结论

本文以解耦并联机构非线性动力学中的混沌现象为研究目标，分含间隙与不含间隙、不同径向间隙大小、不同驱动速度三种情况，对含间隙RU-RPR解耦并联机构进行动力学仿真和混沌现象辨识。对比分析结果表明：间隙运动副对机构动平台的位移和速度影响较小，而动平台加速度会产生比较大的波动；减小运动副径向间隙，有利于减小运动副元素之间剧烈的接触碰撞；增大驱动速度机构运动趋于稳定。

通过分析所绘制的Poincare映射图，证实了含间隙RU-RPR两转动解耦并联机构中确实存在混沌现象。不同间隙值时机构混沌现象的影响对比分析表明，混沌现象随着间隙值的减小而减轻。

本文是对解耦并联机构混沌现象研究的有益尝试，有利于推进并联机构动力学理论研究的深化，也是对混沌理论应用领域的拓展。

参 考 文 献

[ 1 ] 周凤岐, 孔令云. 一类非线性系统的混沌控制[J].航空学报,2007, 28(6): 1443-1448.

ZHOU Feng-qi, KONG Ling-yun. Chaos control for a class of nonlinear system[J].Acta Aeronautica et Astronautica Sinica,2007, 28(6): 1443-1448.

[ 2 ] Aline S, Marcelo A. Comparative analysis of chaos control methods: a mechanical system case study[J].International Journal of Non-Linear Mechanics,2011, 46(8): 1076-1089.

[ 3 ] Blanchard E D, Sandu C, Sandu A. A polynomial chaos-based Kalman filter approach for parameter estimation of mechanical systems[J].Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME,2010, 132(6): 061404.

[ 4 ] Franck S,Humberto Y, Francesca L. Polynomial chaos representation for identification of mechanical characteristics of instrumented structures[J].Computer-Aided Civil and Infrastructure Engineering,2011, 26(3): 173-189.

[ 5 ] James H T, Saied S S. Chaos in nonlinear dynamic systems: helicopter vibration mechanisms[C]//Mediterranean Conference on Control and Automation.Athens:MED,2007.

[ 6 ] Zukovic M, Cveticanin L. Chaos in non-ideal mechanical system with clearance[J].Journal of Vibration and Control,2009, (15)8: 1229-1246.

[ 7 ] 金国光, 李东福，何颖, 等. 柔性变胞机构中的混沌现象研究[J].天津工业大学学报,2009, 28(4): 58-60.

JIN Guo-guang，LI Dong-fu，HE Ying，et al. Research of chaos of flexible metamorphic mechanism[J].Journal of Tianjin Polytechnic University,2009, 28(4): 58-60.

[ 8 ] 李立, 李开富, 陈永. 平面串联型冗余度机器人的混沌运动研究[J].中国机械工程,2003, 14(17): 1512-1515.

LI Li, LI Kai-fu, CHEN Yong.On the chaotic motion of planar serial kinematically redundant robot[J].China Mechanical Engineering,2003, 14(17): 1512-1515.

[ 9 ] 王国庆, 刘宏昭, 何长安. 非线性接触模型在多间隙机构混沌分析中的应用[J].机械科学与技术,2005, 24(6): 636-638.

WANG Guo-qing, LIU Hong-zhao, HE Chang-an. Application of nonlinear contact model in chaos analysis of a mechanism with clearance joints[J].Mechanical Science and Technology,2005, 24(6): 636-638.

[10] 王三民, 沈允文, 董海军. 含间隙和时变啮合刚度的弧齿锥齿轮传动系统非线性振动特性研究[J].机械工程学报,2003, 39(2): 28-32.

WANG San-min, SHEN Yun-wen, DONG Hai-jun. Nonlinear dynamical characteristics of a spiral bevel gear system with back-lash and time-varying stiffness[J].Chinese Journal of Mechanical Engineering,2003, 39(2): 28-32.

[11] 陈学森, 董海军, 刘晓宁. 含时变啮合刚度的间隙非线性齿轮系统的混沌控制[J].机械科学与技术,2006, 25(9): 1035-1037.

CHEN Xue-sen, DONG Hai-jun, LIU Xiao-ning. Chaos control of a nonliner gear system with clearance and time-varying stiffness[J].Mechanical Science and Technology,2006, 25(9): 1035-1037.

[12] 马洪涛, 薛殿伦. 外部激励下行星换向机构的分岔及混沌[J].中国机械工程,2013,24(23): 3129-3139.

MA Hong-tao, XUE Dian-lun. Bifurcation and chaos of planetary reverse system to external excitation[J].China Mechanical Engineering,2013,24(23): 3129-3139.

[13] 谢进, 刘朝晖, 陈永. 驱动关节运动已知的平面2R欠驱动机械臂混沌运动的分析[J].机械设计与研究,2013(增刊1): 254-256.

XIE Jin, LIU Zhao-hui, CHEN Yong. Kinematic analysis of 2R planar underactuated manipulator with knowing the motion of the actuated joint[J].Machine Design and Research,2013(Sup1): 254-256.

[14] Zhang J G,Chu Y D, Li X F, et al. Using proportional and different controller to control chaos in non-autonomous mechanical system[J].International Journal of Modelling, Identification and Control,2009, 8(1): 4-9.

[15] Hou Yu-lei, Zeng Da-xing, Zhang Zhan-ye, et al. A novel two degrees of freedom rotational decoupled parallel mechanism[J]. Applied Mechanics and Materials,2012, 215/216: 293-296.

[16] 侯雨雷, 张占叶, 胡鑫喆, 等. 新型两转动自由度完全解耦并联机构及其特性[J].哈尔滨工业大学学报,2014,46(9):80-85.

HOU Yu-lei, ZHANG Zhan-ye, HU Xin-zhe, et al. A novel 2-DOF fully decoupled rotational parallel mechanism and its characteristics[J].Journal of Harbin Institute of Technology,2014, 46(9): 80-85.

[17] 王国庆, 刘宏昭, 何长安. 含间隙连杆机构非线性行为研究[J].机械设计,2005, 22(3): 12-13.

WANG Guo-qing, LIU Hong-zhao, HE Chang-an. Research on nonlinear behavior of link mechanism with clearance joint[J].Journal of Machine Design,2005, 22(3): 12-13.

Dynamics analysis and chaos identification of a decoupled parallel mechanism concerning clearance

HOUYu-lei1,ZHANGZhan-ye1,LIMing-yang1,WANGYi1,ZENGDa-xing1,LIHui-jian2(1. School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China；2. Key Laboratory of Mechanical Reliability for Heavy Equipments and Large Structures of Hebei Province, Yanshan University, Qinhuangdao 066004, China)

Abstract:Taking a two-rotational independent decoupled parallel mechanism as an object, the structure composition of the mechanism was described.Considering the clearance condition exists in the assembly and operational process, the dynamics model was established in this paper.The dynamics simulation was performed based on ADAMS software, and the variation conditions of the displacement, velocity, acceleration and contact force of the mechanism corresponding to the presence or absence of the kinematic pair clearance, different pair clearance and driving velocity were analyzed.The chaos phenomenon in the dynamics behavior of the decoupled parallel mechanism was identified with the Poincaré section-mapping method, the Poincaré maps were plotted, and the effects of the clearance on the dynamic characteristics of the mechanism were revealed.The results showed that there exists the chaos phenomenon in the decoupled parallel mechanism concerning clearance, which is certainly significant for further nonlinear dynamics research.

Key words:decoupled parallel mechanism; clearance; dynamics; chaos identification

中图分类号:TH113

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.034

通信作者李慧剑 男，博士,教授,博士生导师，1960年生

收稿日期：2014-12-16修改稿收到日期：2015-04-30

基金项目：国家自然科学基金资助项目(51205339;51305384)；中国博士后科学基金资助项目(2013M541199)

第一作者 侯雨雷 男，博士后，教授，1980年生