内嵌倾斜压电柱复合材料板的压电振动特性分析

成建联， 刘含文， 王　越， 陈　炜(长安大学 公路养护装备国家工程实验室，道路施工技术与装备教育部重点实验室，工程机械学院，西安　710064)



内嵌倾斜压电柱复合材料板的压电振动特性分析

成建联， 刘含文， 王越， 陈炜(长安大学 公路养护装备国家工程实验室，道路施工技术与装备教育部重点实验室，工程机械学院，西安710064)

摘要：针对1-3型内嵌倾斜压电柱复合板结构，建立压电复合板结构的有限元模型，并推导出变形关系和形函数;应用拉格朗日方程，建立了单元结构的运动方程。针对不同倾斜角度压电柱复合板进行有限元仿真分析，研究了复合压电板的正压电特性，并对复合压电板的能量损耗因子进行分析。研究结果表明：在相同压力下，压电柱的倾斜角度对复合板的弯曲模态频率影响较大。随着压电柱体倾斜角度的增大，模态频率降低，弯曲变形增大；同时，倾斜柱体棱长变长，产生电压增大。悬臂板在压力作用下，沿宽度方向产生反对称电势。在压电陶瓷柱的倾角达到57°时，损耗因子达到最大。采用内嵌式倾斜压电柱复合板结构，降低了压电板的脆性，保证大尺寸压电板的结构均匀性和应用。

关键词：内嵌倾斜压电柱；压电复合板；压电效应；损耗因子

压电材料具有正逆压电效应，即可作为传感器又可作为作动器，并且具有低质量、宽频带,高灵敏度和容易安装等特点,非常适合于空间结构的振动控制。压电类智能结构是一个新兴的多学科交叉的前沿研究领域,在机器人、航天器、潜水器等领域具有广阔的应用前景,关于压电元件的致动与传感机理的研究在国际上受到广泛关注。目前已经研制出了0-3型、2-2型、1-3型等多种结构的压电复合材料。其中1-3型压电复合材料是由一维的压电陶瓷柱平行地排列于三维连通的聚合物中而构成的具有压电效应的两相压电复合材料。采用这种方式，压电陶瓷柱在黏弹性材料中产生剪切和压缩双重作用，可以提升复合材料的阻尼作用。这种压电陶瓷复合材料既可以粘贴在结构表面也可以嵌入在结构的内部用以控制结构的振动。

复合材料的阻尼特性采用压电陶瓷柱的纵向应变调整来控制，用以提高能量的耗散和控制系统的动力学行为。1-3型压电复合材料由于在某种程度上克服了纯压电陶瓷在强度、脆性方面的缺陷，同时大大增大了其在纵向的耦合系数。有限元分析方法的应用也使压电陶瓷在理论方面分析大大加强。Tzou等[ 1 ]提出了一种包含电势自由度的压电有限元模型,并采用该有限元模型分析了一个具有分布式压电传感器和作动器平板的动力学性能。Ha等[2]利用8节点三维体单元,研究了承受力学和电载荷的包含分布式压电陶瓷片的层状复合结构的动力学和静力学问题。Hauke等[3]采用有限元方法模拟了1-3型压电复合材料的性能并和实验数据进行了比较分析。Hossack等[4]用有限元方法分析了1-3 型压电复合材料中压电柱为方形、圆柱形、三棱柱时机电耦合系数及其波速特性，得到了压电柱在几何界面不同情况下的等效机电耦合系数及等效波速曲线。Reynolds等[5]采用有限元的方法结合实验数据分析了1-3 型压电复合材料陶瓷柱的高频径向谐振，结果证明陶瓷柱间的谐振模式是由于拉姆波(Lamb waves)通过柱间的聚合物传播而形成。Steinhausen[6]用有限元模型分析了1-3 型压电复合材料，在不同陶瓷相含量和不同纤维分布模式下的等效弹性常数、电场参数，并与实验值和理论值进行了比较，经过一定的修正就可以按所需的参数设计1-3型压电复合材料的模型。Arafa等[7]研究了1-3型压电复合材料用于梁的非线性行为的控制，得到较好的减振效果。

压电复合材料在国内受到很多学者的广泛关注，对压电复合材料理论和工艺方面的研究也开展得比较广泛。仲林建等[8]研究了1-3 型压电复合材料各性能参数随PZT体积比变化的曲线、通过有限元软件对1-3型压电复合材料进行了振动模式分析，包括压电材料振动的共振、反共振频率、谐振动以及静水压分析，利用割模-浇铸法制作了1-3 型压电复合材料，并对其性能进行了测试及分析。李莉等[9]根据Chan的1-3型复合材料理论模型和Newnham的复合材料串并联理论,提出了一种用于计算新型1-3-2型压电陶瓷/聚合物复合材料的介电常数和压电常数的理论模型。并进行了实验与理论分析对比，具有较好的符合精度。周勇等[10]进行了压电复合材料层合板弯曲变形及脱粘损伤的有限元分析，提出的四节点压电复合材料层合矩形板弯曲单元,对表面粘贴有压电驱动器的复合材料层合板在外加电场和外载荷作用下的弯曲变形进行了分析。在大量的研究工作中，1-3型压电复合材料大多数采用的是垂直压电陶瓷结构与聚合体之间的复合，这种结构往往主要考虑压缩应变[11]。

本文针对板壳型结构, 研究了使用压电复合材料的自适应结构的振动控制。建立倾斜压电陶瓷柱复合材料板的三维有限元模型，考虑压电陶瓷与聚合体之间的耦合效应，得出单元的运动方程和能量耗散因子。通过数值模拟，研究压电复合板的压电振动特性和能量耗散因子，即结构参数对压电复合材料板阻尼特性的影响，体现压电复合板用于结构振动控制的有效性。

1压电复合材料板的有限元模型

1.1模型与变形关系

图1为复合压电材料板的单元模型，压电陶瓷与z方向的夹角为β，压电复合材料板为薄板，用u,v,w分别表示x,y,z方向的位移，θx和θy分别表示板沿x和y方向的角位移。下标1、2、3分别表示上、中、下各层结构。假设底板和上覆板的中面不产生变形，复合板在弯曲时厚度的变化忽略不计；压电陶瓷和上下板在变形时无能量损失；聚合体为线性黏弹性材料且纵向应力忽略不计。考虑结构能耗的剪切弹性模量表示为G=G*(1+iη)，其中G*为剪切贮能模量，η为耗能因子。所有的各层被牢固地黏接在一起，不存在松动现象。

根据变形关系，板的角位移为：

(1)

图1　压电复合材料板的单元模型Fig.1 Finite element model of piezoelectrical composite

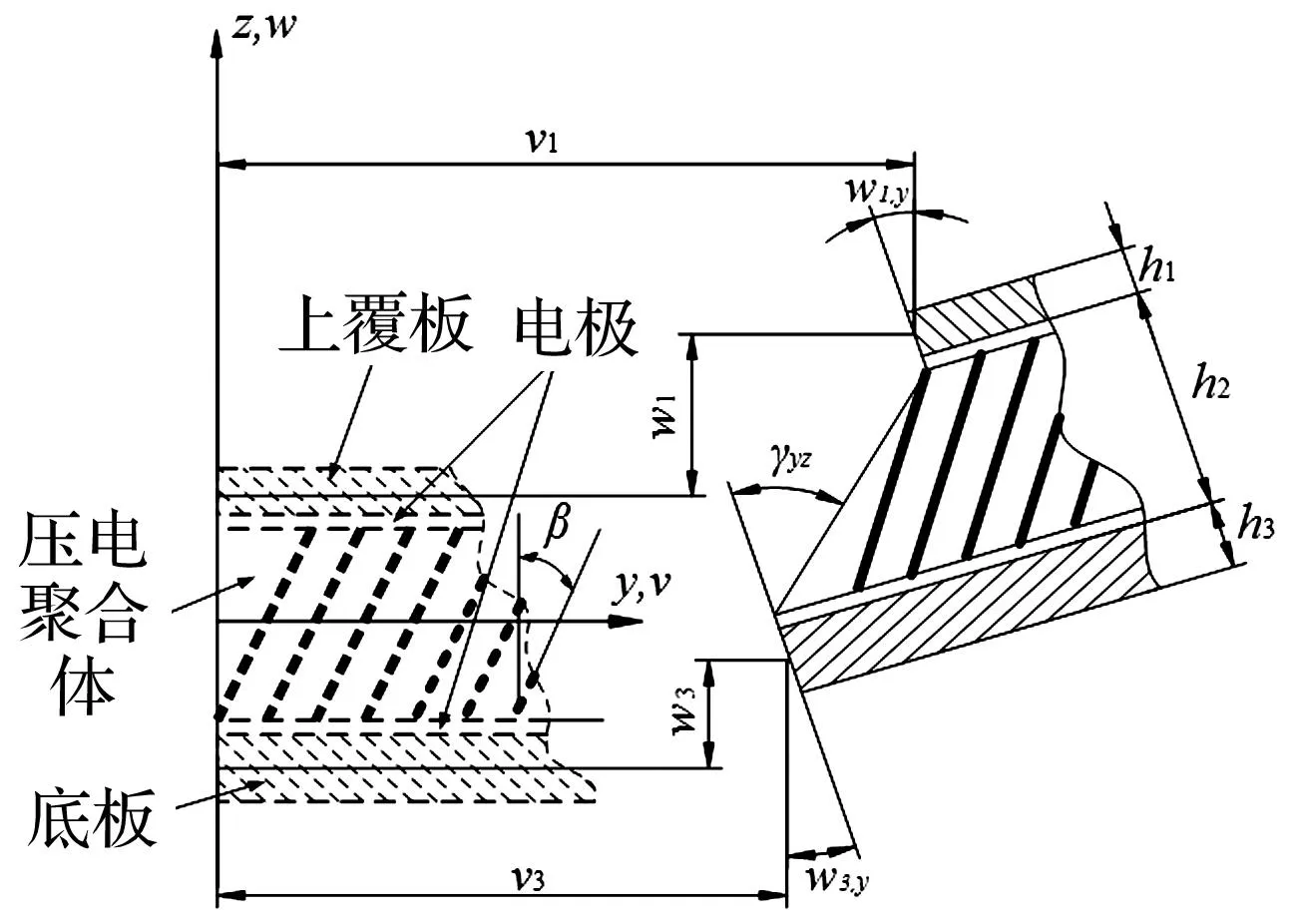
图2　压电复合材料板单元的几何变形Fig.2 Geometric distortion of piezoelectric composite plate element

对于压电复合材料板单元，上、下板的运动参数沿纵向、横向和转动方向发生运动，如图2所示变形过程。压电陶瓷聚合体沿中面的剪切变形可以表示为：

y方向：

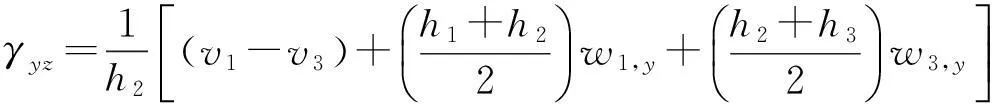
x方向：

式中，下标x和y表示对各自的偏微分、考虑到压电聚合体相对于板后较薄，假设压电聚合体的横向位移w2沿厚度方向线性变化，可表示为:

(4)

1.2单元自由度和形函数

考虑采用四边形单元，每个单元有4个节点，对每个节点采用10个自由度进行描述，上下两层板的中点分别用两个纵向、一个横向和两个角转动位移表示，如图3所示。

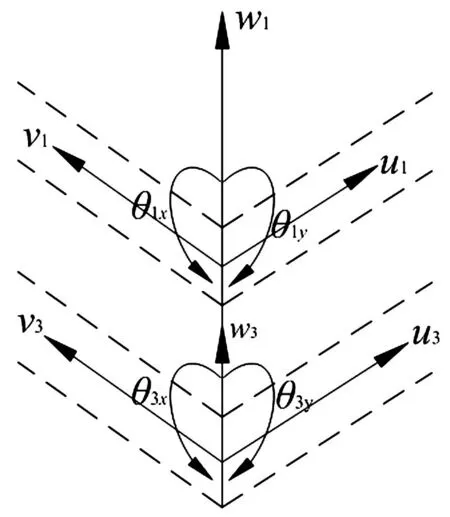
图3　复合材料单元节点自由度Fig.3 Freedom degree of the composite material node

采用多项式表示纵向和横向的位移如下：

(5)

考虑扭转位移，综合式(5)得到

{u1v1u3v3w1θx1θy1w3θx3θy3}T=

[P]{a}T

(6)

式中，[P]=[1xyx2xyy2x3x2yxy2y3x3yxy3]，{a}={a1a2a3…a40}T。

通过式(5)可以表示节点的自由度矢量为：

{δe}=[C]{a}

(7)

式中,[C]为系数矩阵。应用式(6)和式(7)，得到

{u1v1u3v3w1θx1θy1w3θx3θy3}T=

[P][C]-1{δe}=[A]{δe}

(8)

式中,[A]称为形函数矩阵。为了便于计算，将矩阵[A]的十列作为10个矢量，用来表示节点自由度矢量。于是就有

u1={A1}{δe},v1={A2}{δe}

u3={A3}{δe},v3={A4}{δe}

w1={A5}{δe},θx1={A6}{δe}

θy1={A7}{δe},w3={A8}{δe}

θx3={A9}{δe},θy3={A10}{δe}

(9)

压电聚合体层的横向应变可以表示为

(10)

横向剪切应变也可表示为

(11)

(12)

综合式(10)～式(12)，可以得到压电聚合体的应变矢量{S}为

(13)

2结构单元运动方程

2.1上、下层板的应变能

上、下层板的应变能由弯曲、扭转和拉伸三部分产生的应变能组成。根据弹性理论，由弯曲和扭转产生的应变能可表示为

UB+UT=

(14)

式中，E和μ分别表示弹性模量和泊松比。用式(9)，上述公式可以表示为

2μ1{A5,yy}T{A5,xx}+{A5,yy}T{A5,yy}+

2(1-μ1){A5,xy}T{A5,xy}]dxdy{δe}+

2μ3{A8,yy}T{A8,xx}+{A8,yy}T{A8,yy}+

2(1-μ3){A8,xy}T{A8,xy}]dxdy{δe}

(15)

上、下层板在应力作用下产生的应力-应变关系为

(16)

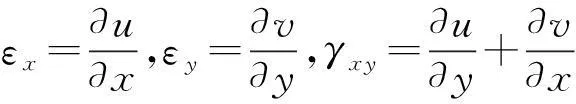
{σ}=[D]{ε}

(17)

则应变能可以表示为

(18)

将式(16)和(17)代入式(18)，得

(19)

将式(19)扩展开来，可以得到

(20)

将式(9)代入式(20)，得到

2μ1{A2,y}T{A1,x}+{A2,y}T{A2,y}+

(21)

式中，{A1,y;2,x}={A1,y}+{A2,x},{A3,y;4,x}={A3,y}+{A4,x}。

2.2压电陶瓷聚合体应变能

根据Yang[12]得出的压电陶瓷聚合体的本构关系:

{T}=[R]{S}-{d}Ez

(22)

式中，{T}表示应力，{S}表示应变，[R]为系数矩阵，{d}为位移，Ez为电场。压电聚合体单元的应变能表示为

(23)

将式(22)代入式(23)可得

Ez{R}-1{d}Ez]dV=

(24)

从式(24)可以看出，压电聚合体的应变能由正应变、剪切应变能，能量耗散和电场做功三部分构成。

压电复合层板单元的总应变能为

(25)

式中，[Ke]为单元的刚度矩阵，其表达式为

(26)

2.3压电复合材料板单元的动能

单元的动能可以为

(27)

式中，ρ为各层材料的密度，压电聚合体层的密度为ρ2=ζcρc+(1-ζc)ρp，ζc为压电陶瓷所占的百分比，ρc和ρp分别为压电陶瓷和聚合体的密度。由式(9)可以将动能表达式简写为：

(28)

式中，[Me]为质量矩阵，其表达式为

{A4}T{A4}+{A5}T{A5}]dxdy+

{A5}T{A8}+{A8}T{A8}]dxdy

(29)

2.4单元运动方程

系统的拉格朗日方程

(30)

式中，

(31)

求式(30)中的各项，其结果如下：

(32)

(33)

因此，可以得出单元的运动方程为

(34)

式中，{Fe}表示由压电陶瓷聚合体单元产生的力和力矩矢量，其表达式为

(35)

最终，可以得到压电复合材料板单元的运动方程为

(36)

如果考虑不同的结构单元、边界条件和控制策略，可以将运动方程式(36)应用于整个压电复合材料层板系统。其运动方程可以表示为

(37)

采用式(37)可以预测结构在开环或闭环控制作用下的动态响应。在闭环控制时，电场Ez需要根据反馈控制作用下的位移大小来确定。电场能被表示为

Ez=-{Kg}{δ}=-gds{C}{δ}

(38)

式中，{Kg}为增益矩阵，gd为微分控制增益系数，s为拉氏算子，s=iω。系统的运动方程可以表示为

(39)

则系统的有效刚度为

[Keff]=[K]+{f}(gdiω){C}

(40)

因此，系统总的能量可以表示为

(41)

其中压电复合体储存能量耗散系数η定义为

(42)

考虑损耗系数并结合压电复合材料本构关系，可以确定结构设计参数，并根据最大能量耗散特性可以对参数进行优化设计。

3仿真分析

3.1材料选用与边界条件

为了解内嵌压电陶瓷板的压电特性，采用100 mm×20 mm×7 mm，顶板和底板之间的距离为5 mm。压电柱采用2 mm×2 mm的方柱，柱之间的间隔为4 mm，倾斜角度β在0°～90°变化，顶板作用0.1 MPa的压力，压电材料选用常用的PZT-5H，上下板之间采用聚合体—软性聚丙烯填充，密度为0.86×103kg/m3。压电板采用悬臂结构，忽略非线性因素，其边界条件为：在y=0处，u=v=w=0，θx=θy=0；在z=1 mm处，V=0；并且电场Ex=Ey=0，在xy，xz平面剪切应变为Sxy=Sxz=0；同时考虑聚合体与陶瓷柱，在yz平面具有相同的剪切应变，在z方向具有相同的电场，在y方向电位移均为零。选用材料特性如表1、表2所示。

3.2分析结果

根据节点的位移变化，用以区分横向振动、面内振动和扭曲振动。图4所示为悬臂板的模态频率，从表中可以看出，板沿厚度方向的1阶、3阶和6阶横向振动模态频率随着压电柱的倾斜角度增大而逐渐降低，频率越高降低幅度越大；而沿板的宽度方向面内振动和扭曲振动，压电柱的倾角影响不大。

图5是针对板长方向在力的作用下位移的变化曲线，图中显示出随着压电柱倾斜角度的增加，同一位置点处悬臂板的位移变形也在增大，但其变化的幅度相对较小。图6显示压电柱沿其棱边的高度方向在力的作用下产生电势的变化，由于受倾斜影响，压电柱的棱长各不相同，角度越大，棱边越长，其产生的最大电压越高，沿棱柱长度呈现非线性变化。图中显示现象可解释为，零电位点确定为中间平面，材料没有发生应变，中间平面在棱柱中点偏下位置。在中间平面下部，压电陶瓷柱承受剪切和受压，产生负电压，数值变化较小，同时各角度棱柱中间平面距离底面高度变化较小，使最大应变位置和对应的反转点位置变化较小；而在中间平面上部，随着倾斜角度的加大，棱柱的边长加长，压电陶瓷柱承受剪切和拉伸作用比较明显，产生正电压，应变和系数值比较大，使电压数值变化较大，同时，最大应变位置点距离中间平面位置变高，相对应的正压反转点也变高。

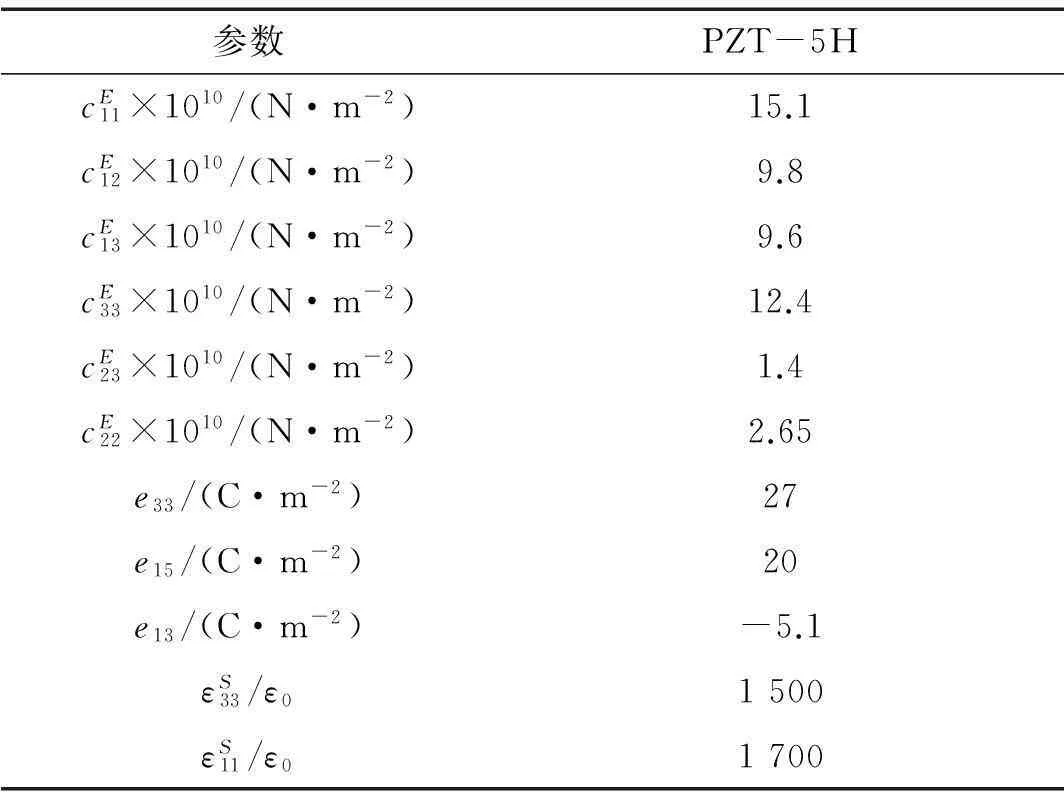
表1　压电柱材料的物理特性

表2　软性聚丙烯材料物理特性

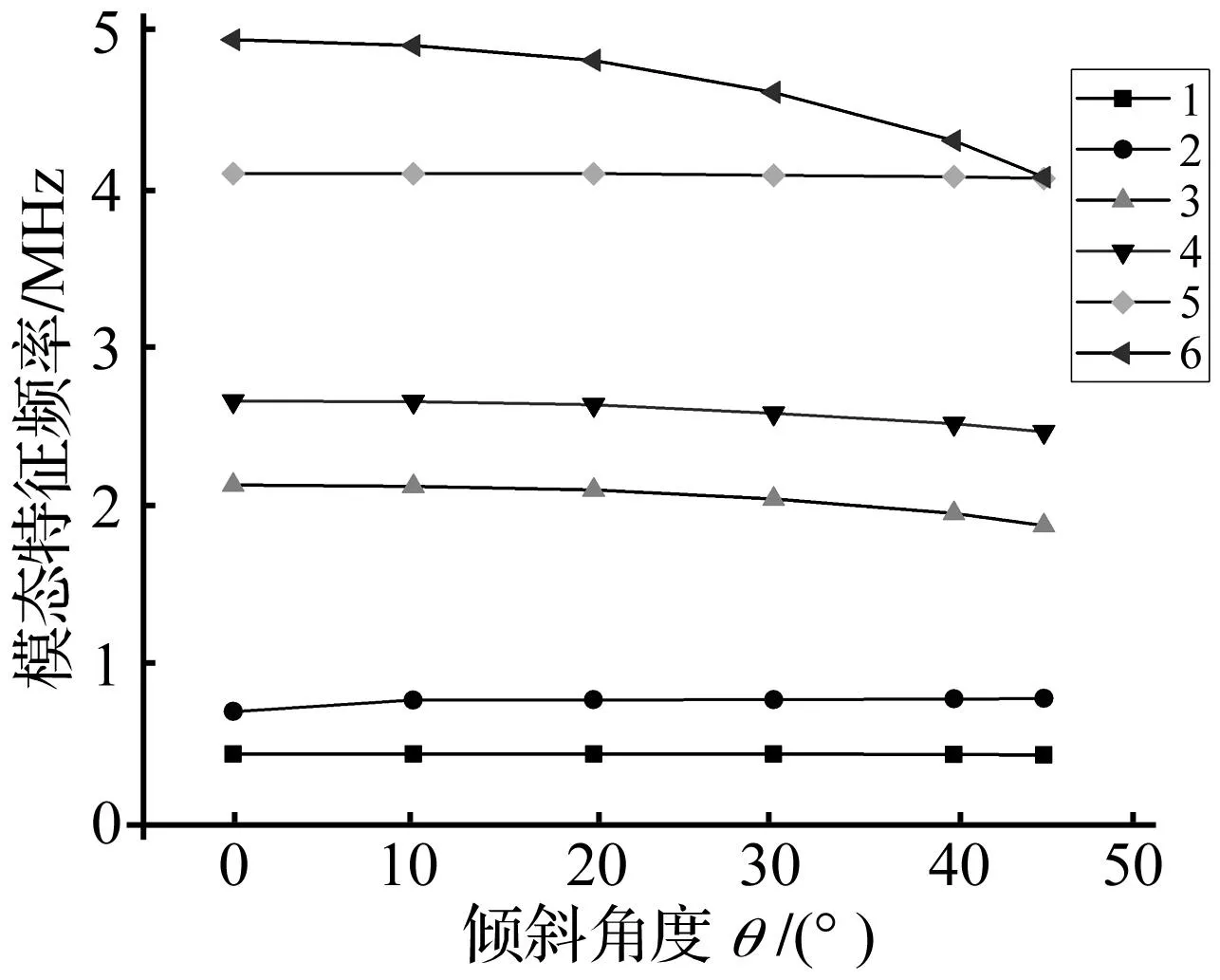
图4　不同倾角压电柱下板的模态特征频率Fig.4 Modal frequency of plate with different incline angle piezo-pillar

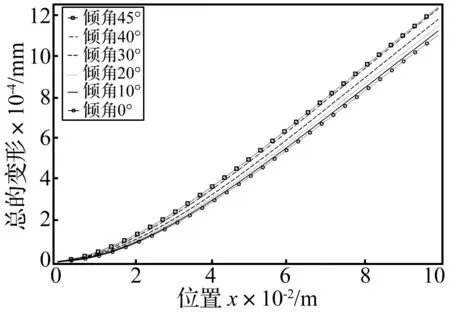
图5　压电悬臂板沿长度方向的位移变化Fig.5 The displacements of piezoelectric cantilever plate along the direction of length

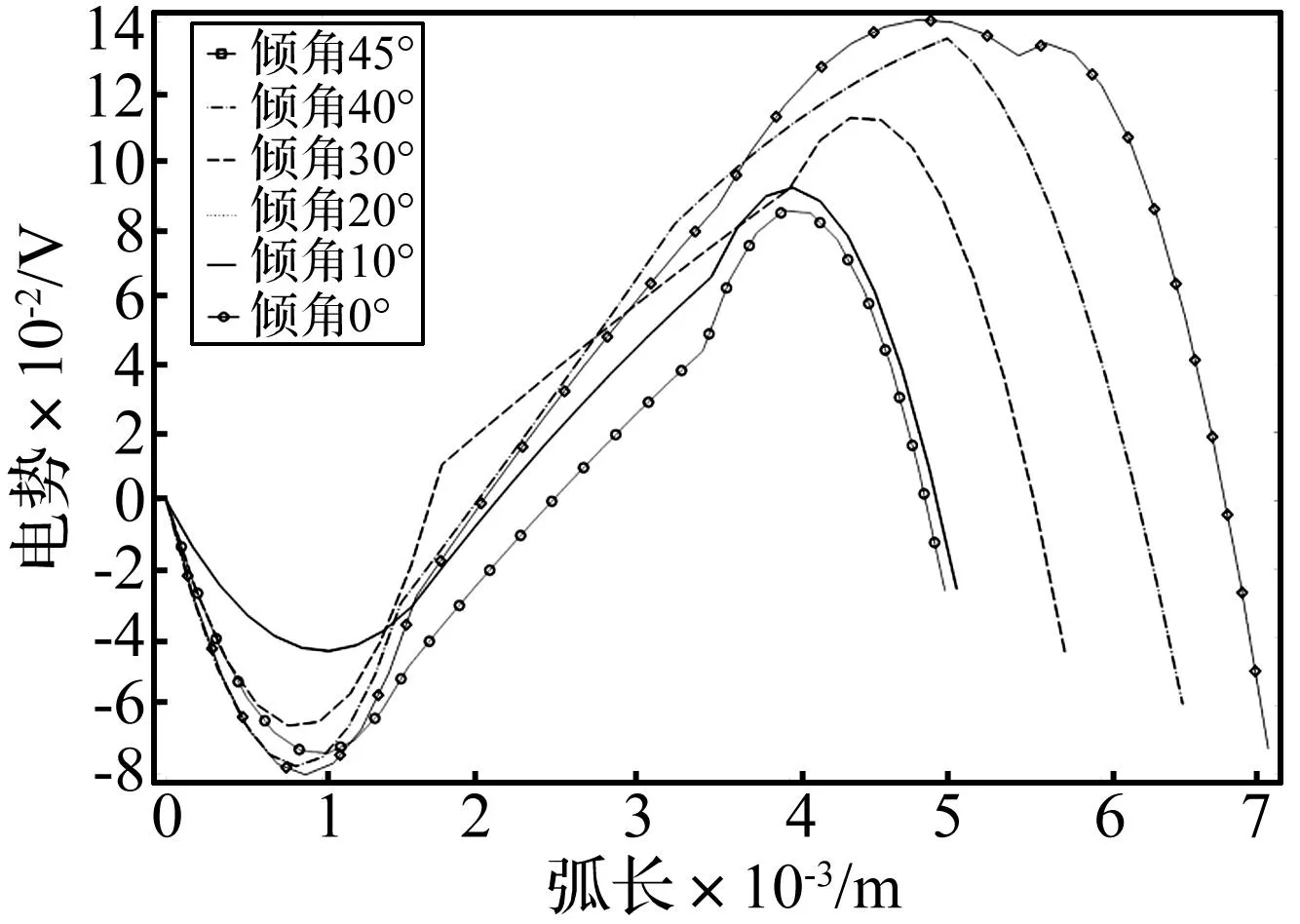
图6　压电柱沿棱柱高度的电势变化Fig.6 Electric potential of piezo-pillar along height of side

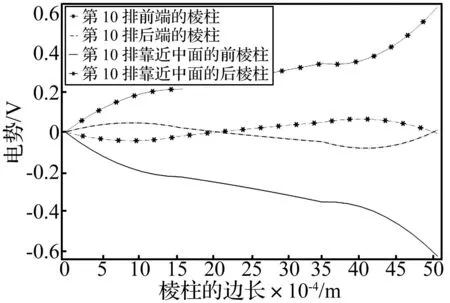
图7　沿板的宽度方向压电柱侧棱的电势对称变化Fig.7 Symmetrical electric potential of piezo-pillar along the width direction of plate

在仿真分析过程中发现有趣的现象，就是对由内嵌倾斜四棱柱复合板，在压力作用下，板的两边在棱柱上产生反对称的电势(如图7、8所示)，沿着板的宽度方向，产生的电势呈现对称状态。也就是说，在板宽度方向的中面上，其电势为0。这是由于在x方向剪切应变导致的结果，而在中面位置的剪切应变为零。因此，对于这种复合结构的压电板在使用时需要注意此特征，以确定电极的连接位置。并且通过多尺寸仿真分析，随着板的宽度增大，复合板的抗弯刚度增大，相同长度位置处，板边沿的倾斜棱柱产生的电势越低。根据板的弯曲特点，在其长度方向，越靠近端部，其应力越小，其产生的电势也越小，体现了压电材料在力的作用下产生电势的特性，其电势的产生主要依靠剪切和压缩的共同作用，端部只有压缩作用，因此，电势也越低。分析可知，在其端部压电柱的最大电势仅有5 mV。

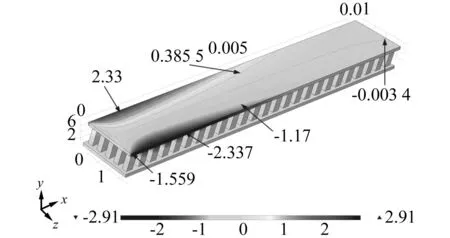
图8　在压力作用下压电复合板产生的电势云图Fig.8 Electric potential contour of composite plate under pressure

图9是压电柱倾斜角度对压电复合板的损耗因子影响变化曲线，图中显示在三种不同控制增益下损耗因子的变化曲线，其增益考虑其无量纲化,Gd=gdω/L，取Gd={1010,5×1010,1011}。从图中数据显示，在现有结构下压电陶瓷柱的倾斜角度达到57°时，损耗因子达到最大，在这个角度下，由于压缩和剪切的综合作用，使总的能量损失达到最大。倾斜角度在小于20°范围内，损耗因子变化较小，在超过最大值后，损耗因子随着倾斜角度的增大快速下降。在增益为1011下，θ=0°时压电柱承受纯压缩作用，这时的损耗因子约为0.154；θ=90°时压电柱承受纯剪切作用，损耗因子约为0.077，而综合作用下损耗因子最大约为0.205。从图中三种增益控制显示，增益越大能量损耗也随之增大。

4结论

(1) 应用拉格朗日方程，建立内嵌倾斜压电柱体复合板的有限元模型，结合压电陶瓷本构关系，得出单元的刚度矩阵[Ke]和质量矩阵[Me]的表达式，得到复合材料板单元的运动方程。

(2) 压电复合板沿板厚方向的模态频率随着压电柱倾斜角度的增大而降低，而侧向振动的模态频率几乎不受影响。

(3) 在同样作用力下，压电柱的倾斜角度越大，其抵抗变形的能力越差。在压力作用下，压电复合板的压电棱柱沿厚度方向产生反对称电动势，棱柱距离中间平面越远，其产生的电势越高。

(4) 能量损耗受压电柱倾斜角度和控制增益的影响，随着增益的增大，损耗因子变大。数值模拟结构的最大损耗因子发生在压电柱倾斜角度57°处。通过结构参数设计可以有效控制压电复合陶瓷板的阻尼。

(5) 本文采用此结构形式的压电复合板，作为一种新结构压电复合材料，在使用上与常规的压电板没有差异。采用倾斜棱柱结构，倾斜角在一定的数值范围内复合板压电性能优于倾斜角零度(垂直柱)的结构。但新结构使柱面只受垂直压力变为同时受垂直压力和切向力，从而增加了复合板正向和切向被破坏的风险；此外，倾斜结构使高度增大的尺寸转化为横向增大,这样占用空间并未减少，而使结构稳定性变差。

总之，本文提供了一种能权衡压电效率和负面影响综合结果的压电板结构设计途径。

参 考 文 献

[ 1 ] Tzou H S, Tseng C I. Distributed piezoelectric sensor/ actuator design for dynamic measurement/ control of distributed parameter systems: a piezoelectric finite element approach[J].Journal of Sound and Vibration, 1990, 138 (1): 17-34.

[ 2 ] Ha S K, Keilers C, Chang F. Finite element analysis of composite structures containing distributed piezoceramic sensors and actuators[J].AIAA Journal, 1992, 30(3): 772-780.

[ 3 ] Hauke T, Steinhausen R, Seifert W, et al. Modeling of poling behavior of ferroelectric 1-3 composites[J].Journal of Applied Physics, 2001, 89(9):5040-5047.

[ 4 ] Hossack J A, Hayward G. Finite-element analysis of 1-3 composite transducers[J].IEEE Trans U FFC, 1991,38(6):618-629.

[ 5 ] Reynolds P, Hyslop J, Hayward G. Analysis of spurious resonances in single and multi-Element piezocomposite ultrasonic Transducers[C]//IEEE International Ultrasonics Symposium (IUS),2003:1650-1653.

[ 6 ] Steinhausen R, Hauke T, Sifert W, et al. Fine scaled piezoelectric 1-3 composites: properties and modeling[J].Journal of the Europe Ceramic Society, 1999, 19:1289-1293.

[ 7 ] Arafa M, Baz A. On the nonlinear behavior of piezoelectric actuators[J].Journal of Vibration and Control,2004,10(3):387-398.

[ 8 ] 仲林建，陈俊波，王世全. 1-3型压电复合材料的制备及性能分析[J].声学与电子工程，2007，85(1)： 31-34.

ZHONG Lin-jian, CHEN Jun-bo, WANG Shi-quan. Manufacture andperformance analysis of 1-3 piezoelectric composites[J].Acoustics and Electronics Engineering,2007,85(1):31-34.

[ 9 ] 李莉,秦雷,万媛媛，等. 1-3-2型压电陶瓷/聚合物复合材料的理论模型[J].功能材料与器件学报, 2007,13(4):339-344.

LI Li, QIN Lei,WAN Yuan-yuan,et al. Model for 1-3-2 piezoelectric ceramic/polymer composites[J].Journal of functional Materials and Devices, 2007, 13(4): 339-344.

[10] 周勇, 王鑫伟, 孙亚飞, 等. 压电复合材料层合板弯曲变形及脱黏损伤的有限元分析[J].吉林大学学报:工学版, 2004, 34(2):180-184.

ZHOU Yong, WANG Xin-wei, SUN Ya-fei, et al.Finite element analyses for piezoelectric laminated plate in bending and actuator debonding[J].Journal of Jilin University of Technology:Natural Science Edition,2004,34(2):180-184.

[11] 水永安. 压电复合材料的理论模型[J].物理学进展, 1996, 16(3/4): 353-361.

SHUI Yong-an. Theoretical model of piezoelectrical composite material[J].Progress of Physics,1996,16(3/4):353-361.

[12] Yang Jia-shi. The mechanics of piezoelectric structures[M].Singapore:World Scientific Publishing Co. Pte. Ltd., 2006.

Analyzing characteristics of composite-plate-embedded sloping piezoelectrical pillars

CHENGJian-lian,LIUHan-wen,WANGYue,CHENWei(Highway Maintenance Equipment National Engineering Laboratory, Key Laboratory of Road Construction Technology and Equipment Ministry of Education, School of Construction Machinery, Chang’an University, Xi’an 710064, China)

Abstract:Piezo-composite plate consists of 1-3 type piezoelectrical pillars that are obliquely embedded in a viscoelastic soft polypropylene matrix.The finite element model (FEM) is developed to investigate the positive piezoelectrical properties and the energy-dissipation characteristics of active piezoelectric composites.The strain vectors and shape functions of composite plates are derived from the displacement relations.The motion equations of elements were obtained by using Lagrange’s equation.The loss factor is expressed by the ratio of the dissipation of the stored energy.The effects of the sloping angle of the piezoelectric pillars on the positive piezoelectric properties are shown.The bending mode frequencies and deflections and the positive potentials are analyzed.The antisymmetrical potential appears along the width of a composite plate under pressure.The loss factor of the composite plate is presented for the effect of the sloping angle of the piezoelectric pillars and the control gains considered.The results indicate that the loss factor reaches its maximum at an angle of 57 for the different control gains, and effectively high loss factors may be attained by proper selection of the design parameters of the composite plate.Using the composite plate-embedded sloping piezoelectric pillar can decrease the brittleness of the piezoelectrical plate and ensure homogeneity as well as the application of a larger piezoelectrical composite plate.

Key words:embedded sloping piezoelectric pillars; piezoelectrical composite plate; piezoelectric effect; loss factor

中图分类号:TB381；O326

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.030

收稿日期：2015-01-14修改稿收到日期：2015-03-23

基金项目：国家留学基金委资助项目(201306565032)

第一作者 成建联 男，博士，副教授，1969年9月生