二维晃动自然频率与阻尼比系数的试验识别

王立时， 李遇春， 张　皓(同济大学 土木工程学院，上海　200092)



二维晃动自然频率与阻尼比系数的试验识别

王立时， 李遇春， 张皓(同济大学 土木工程学院，上海200092)

摘要：液体的晃动模态(自然频率、振型与阻尼比系数)是贮液结构设计以及振动控制的重要参数。在液体晃动的模态试验中，需要激发液面的模态运动，但液面的对称模态运动一般较难激发出来，使得对称模态参数(特别是阻尼比系数)难以精确识别。采用参数激振的方法对矩形、U形和圆形截面容器进行竖向激振，容易激发出液体表面的前四阶模态(包括对称模态)运动，撤除激励后液体表面按某一特定的振型作自由衰减振动，通过激光测量液体表面波高的自由衰减曲线，从而精确得到液体晃动的自然频率与对应的阻尼比系数，测得晃动频率与理论频率结果吻合良好，表明该试验识别方法有效。

关键词：二维晃动；参数振动；实验；液体；模态参数

液体晃动问题在工程领域中十分常见，是一种非常复杂的流体运动现象，它会对载体运动产生重要影响，例如：携带液体燃料的航天或航空器，当液体晃动时可能对航天或航空器的正常飞行产生影响；又如：大型储液罐在地震作用下，会引起液体的强烈晃动，由此可能造成储液结构的破坏。考虑液体晃动所带来的不利影响是结构系统设计所必须考虑的重要问题，而液体晃动的模态参数(频率、振型、阻尼系数)是结构系统设计以及晃动控制的重要依据，因而液体晃动的模态识别具有重要的工程意义。

晃动的模态识别包括理论与实验两个方面。Dodge等[1-3]在他们的专著中对液体晃动模态的一般理论及工程应用进行了全面而系统的阐述，对于一些几何不规则的容器，模态的理论求解会遇到较大的困难，而且液体计算理论中的一些假设往往与实际情况有差别，理论计算的结果需要实验验证，因此液体晃动的实验模态识别对于理论与实际工程而言都极为重要。相对于液体晃动的理论研究而言，晃动的实验研究相对要少得多，夏益霖等[4-5]采用理论与试验的方法研究了液体等效力学模型的参数。王为等[6]对半球形容器中液体自由晃动的非线性行为进行了实验研究。

对于任意形状(截面)的二维晃动问题，Hasheminejad等[7]采用保角映射的方法研究了半椭圆截面内液体晃动模态的求解方法，但其计算公式只能适合半椭圆容器。最近Li等[8]基于Ritz方法提出了一个针对任意截面内的二维晃动自然频率的简单近似解析方法，与其它解析与数值解的误差在5%的范围内，但这个方法无法得到可靠的振型。为了得到更高精度的晃动频率及振型，李遇春等[9]针对一般二维晃动问题，提出了一个统一Ritz计算方法来识别晃动模态。然而模态分析的理论结果仍需要实验验证，且液体晃动的阻尼一般也需要实验来确定。

液体的模态识别需要激发液面的晃动，然后通过对液面运动的测量来确定模态参数，在实验中液面的反对称模态通常比较容易激发出来，而纯粹的对称模态比较难以激发出来，本文拟采用参数激振的方法对三种不同容器进行竖向激振，可容易激发出液体表面的前几阶反对称与对称晃动模态，撤除激励后液体表面按某一阶模态作自由衰减晃动，从而可以较精确地测量晃动的频率与对应的阻尼比系数。本文的模态试验识别方法可供相关的液体晃动研究参考。

1实验装置与模型

如图1所示，本文实验装置由激振器(HEV-1000)、信号发生器(SPF05A)、功率放大器(HEA-1000)、加速度计(LC0115 SNW121)、动态信号分析仪(IOTECH 650U)、激光位移传感器(SUNX-ANR 1215)、数据采集仪(INV306U-A)以及数据分析仪(INV306U)组成，试验模型为有机玻璃制作的贮液容器，固定安装在激振器上。

实验时，首先由信号发生器产生一个正弦信号，该信号经由功率放大器放大，然后传送给激振器，从而驱动激振器，给贮液容器(含水)施加一个竖直方向的正弦加速度，容器的竖直加速度由加速度计采集，通过动态信号分析仪进行分析后再由计算机记录下来，激光位移传感器固定在容器上，用于测量液体自由表面的波高随时间的变化历程，激光信号通过数据采集仪、信号分析仪以及电脑监测与记录。

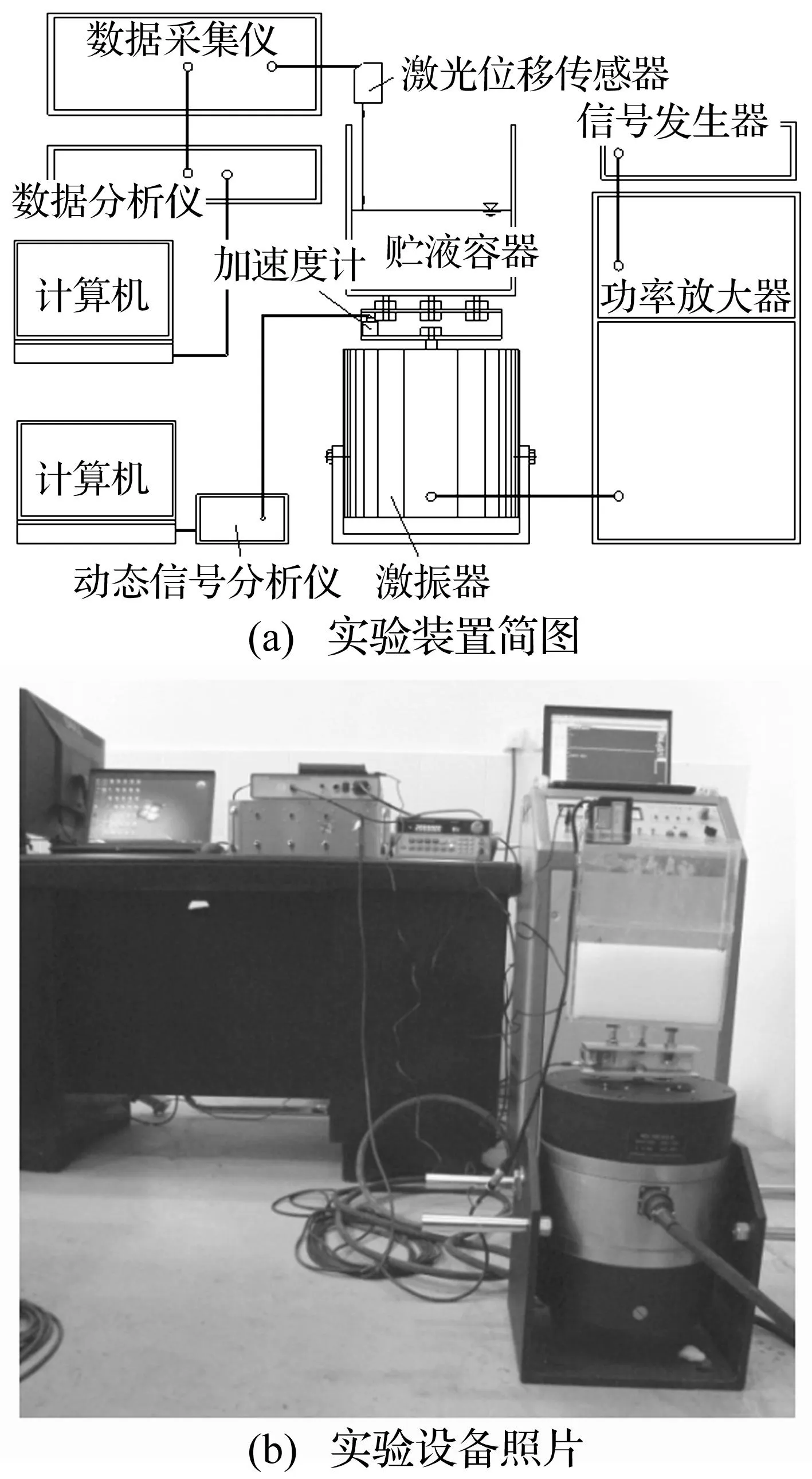
图1　晃动实验装置简图及设备Fig.1 Experiment diagram and devices

实验所用模型为扁平状容器，以模拟液体二维晃动，图2显示三种不同截面形式的实验模型，分别是矩形、圆形和U形容器。矩形容器的内宽为200 mm，圆形容器的内半径为125 mm，U形容器的底部内半径为100 mm，三个容器内腔厚度均为20 mm。容器内的水深因实验工况而有所不同。试验水体中加入了微量的白色染料，以使液体自由表面能反射激光传感器所发射的激光，染料对液体动力学特性的影响很小，可忽略不计，此外，液体中加入了少许清洁剂，以减小液体表面张力对晃动的影响。

图2　三个试验容器Fig.2 Three test tanks

2自由液面波高、频率与阻尼的测量

首先采用近似理论方法[8]，近似估算各种不同形状容器中液体的前四阶晃动自然频率f0j(j=1,2,3,4)，然后对试验模型进行主参数激振[2]，即把激振频率调整为fexitation≈2f0j，这时容器内的液体会发生第j阶模态的主参数晃动(共振)，然后停止激励，液体表面将以第j阶模态作自由衰减运动，根据这个自由衰减运动的时程曲线就可得到第j阶晃动自然频率及阻尼比系数。

晃动的波高可由固定在容器上的激光位移传感器测量，一个典型的实测波高时程响应曲线见图3，波高曲线可包括三部分：① 参数失稳过程，② 稳态响应，③ 停止激励后的自由衰减过程。其中第①部分可用于研究参数晃动的不稳定性质，第②部分用于研究参数晃动的极限环运动(非线性晃动)，关于第①、②的研究将另文讨论。第(3)部分为波高自由衰减曲线，这一部分的测量结果可用于识别晃动的自然频率及阻尼比系数。

需要说明的是，根据参数晃动理论[2]，对于某一固定幅值的激励加速度，在(激振频率=2×自然频率)附近的一个激励频率范围内(即：不稳定区域内)均可激发出液体的第j阶模态的主参数晃动，因此只要理论估计的频率f0j与实际自然频率相差不是太大，通常可容易地激发出第j阶模态的主参数晃动，采用现有的近似理论方法(如文献[8]的方法)得到的近似自然频率完全满足实验的计算精度需求。当发生参数晃动时，这时激励频率严格等于二倍的液面晃动响应频率，液面稳态响应幅值较大(见图3的第②部分)，呈现一种常见的非线性特征，即：(上部)波峰的幅值明显大于(下部)波谷的幅值，这时液面晃动响应频率一般情况下并不等于自然频率，当停止激励后，液面按其第j阶振型作自由衰减运动，当液面晃动幅值逐步减小趋于线性时，液面的晃动频率会略有改变，趋向于(线性)自然晃动频率。

从图3可以看出，自由衰减曲线前一部分晃动振幅较大，在实验数据处理中，为了去掉波形的非线性影响，以获得较精确的晃动自然频率与阻尼比系数ζ，可在衰减曲线中截取一段振幅较小(线性)的时间段(见图4，波峰与波谷的幅值大致相同)进行数据处理，通过对该段衰减曲线进行FFT变换，就可容易得到晃动的自然频率，而阻尼比系数可由下式估计：

(1)

式中：h1及hN+1分别为第1及N+1个振动循环的波高，见图4所示。

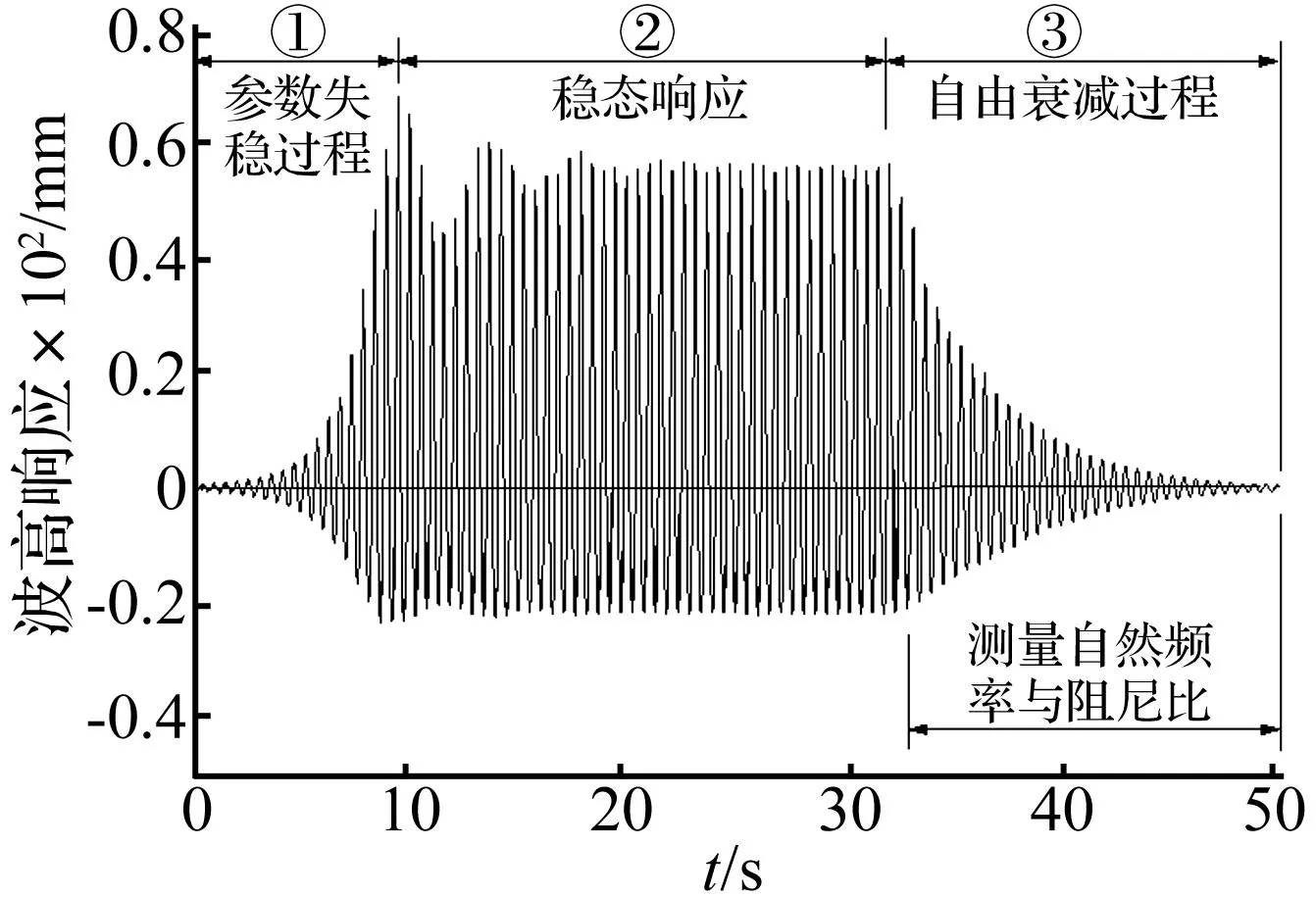
图3　典型的实测波高时程响应Fig.3 A typical measured time-history response of wave-height

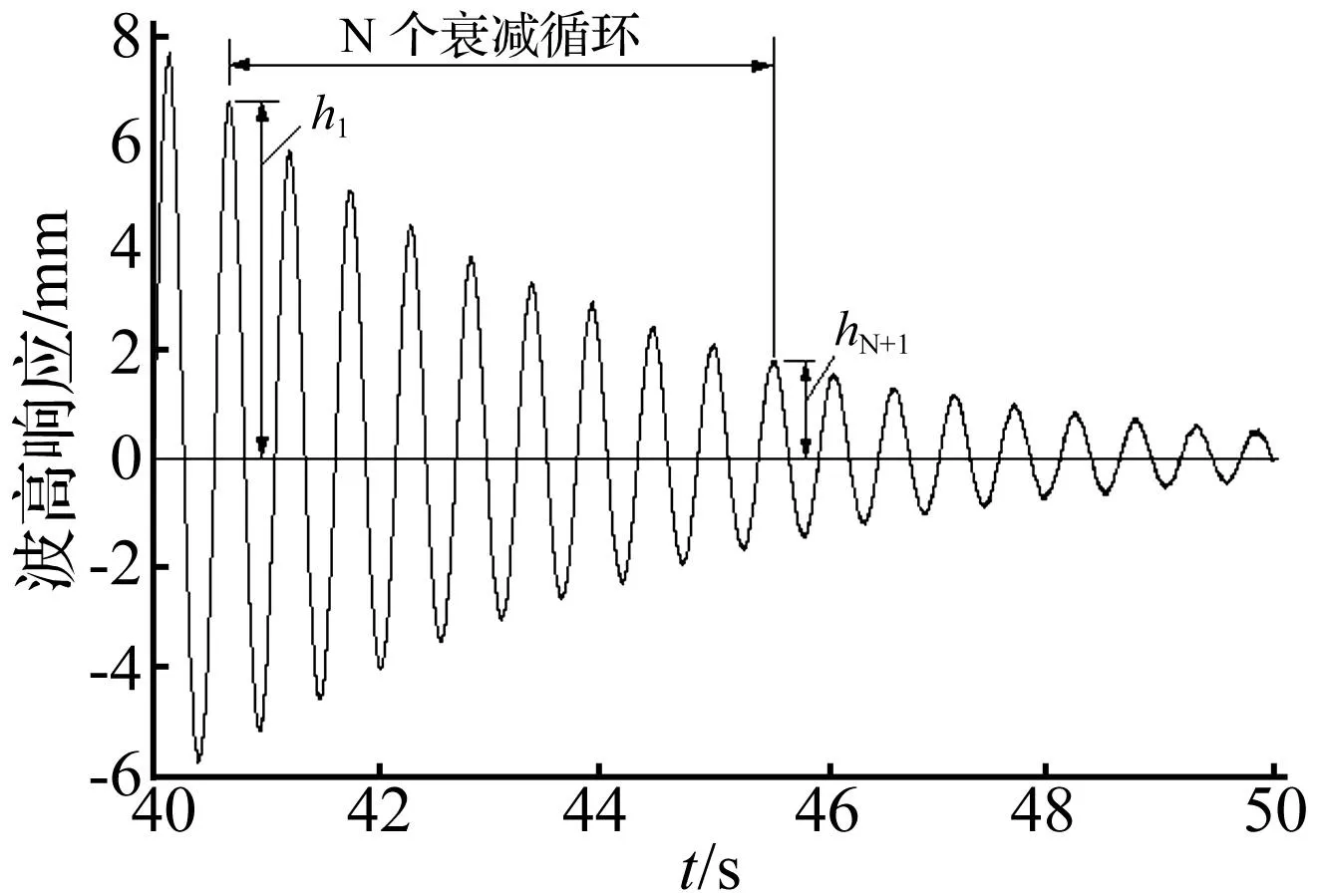
图4　实测波高自由衰减曲线Fig.4 A measured free-decay curve of wave height

3晃动模态的试验结果

3.1矩形容器实验结果

图5为水深h=120 mm，容器半宽a=100 mm的矩形容器前四阶晃动模态。实验按照上述步骤测出了矩形容器内液体的前四阶晃动频率，每阶晃动模态测得六组频率值，求得平均晃动频率，将实验结果列于表1，同时将文献[9]Ritz方法得到的计算结果也列于表1进行对比，从表中看出实测频率与预估的理论频率最大相对误差为2.31%，预估频率与实际频率吻合良好。将每阶模态自由晃动的平均阻尼比系数也列于表1，可以看到阻尼比总体上随模态阶数的增加而略有增大。

图5　矩形容器内前四阶晃动模态Fig.5 The first four sloshing modes in rectangular tank

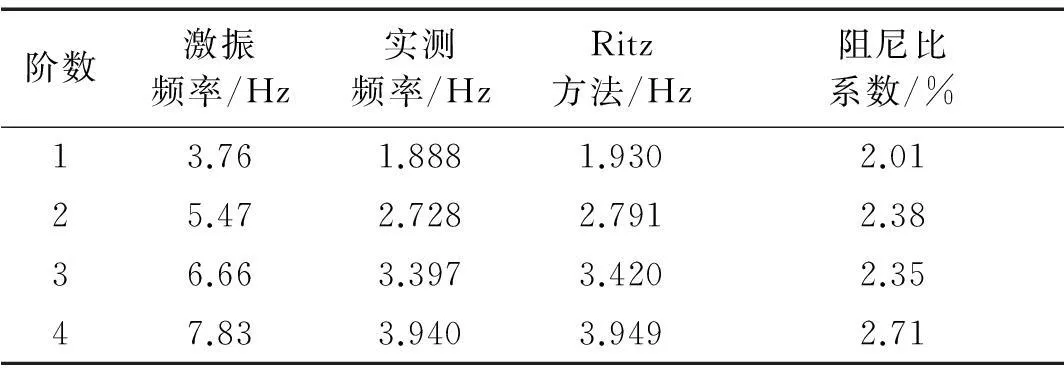
阶数激振频率/Hz实测频率/HzRitz方法/Hz阻尼比系数/%13.761.8881.9302.0125.472.7282.7912.3836.663.3973.4202.3547.833.9403.9492.71

3.2圆形容器实验结果

图6为水深h=160 mm，容器半径R=125 mm的圆形容器前四阶晃动模态。实验按照上述步骤测出了圆形容器内液体的前四阶晃动频率，每阶晃动模态测得六组频率值，求得平均晃动频率，将实验结果列于表2，同时将文献[9]Ritz方法得到的计算结果也列于表2进行对比，从表中看出实测频率与预估频率最大相对误差为4.76%，实验与理论结果吻合良好。将每阶模态自由晃动的平均阻尼比系数也列于表2，可以看到阻尼比系数比较分散。

图6　圆形容器内前四阶晃动模态Fig.6 The first four modes in circular tank

阶数激振频率/Hz实测频率/HzRitz方法/Hz阻尼比系数/%13.341.6811.7652.5324.922.5172.5472.7436.013.0873.1222.1447.003.5133.6052.40

3.3U形容器实验结果

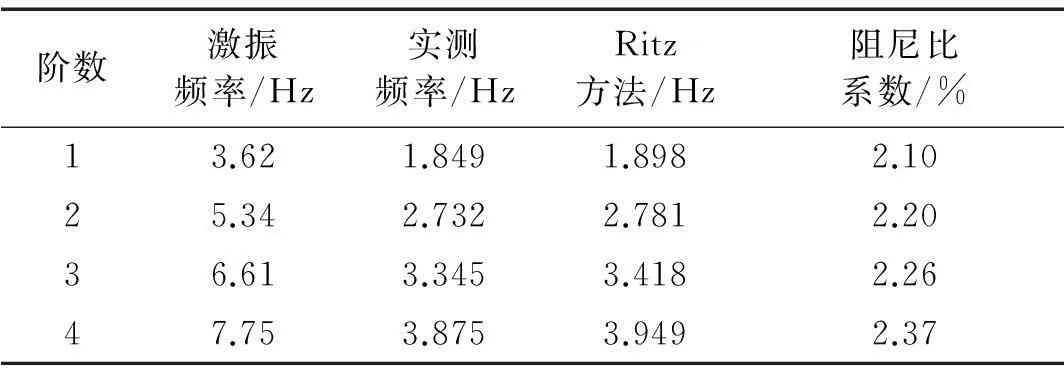
图7为水深h=115 mm，容器半径R=100 mm的U形容器前四阶晃动模态。U形容器内液体的前四阶晃动频率的实验与理论预估值列于表3，从表中看出实测频率与预估频率最大相对误差为2.65%，两个结果吻合良好。将每阶模态自由晃动的平均阻尼比系数也列于表3，可以看到阻尼比总体上随模态阶数的增加而略有增大。

图7　U形容器内前四阶晃动模态Fig.7 The first four modes in U-shaped tank

阶数激振频率/Hz实测频率/HzRitz方法/Hz阻尼比系数/%13.621.8491.8982.1025.342.7322.7812.2036.613.3453.4182.2647.753.8753.9492.37

4结论

本文制作了矩形、U形和圆形容器，利用参数振动的原理，激发各阶稳定晃动模态后撤除加载，从而测量不同容器内液体各阶自由晃动频率与阻尼比系数，测得晃动频率与Ritz方法得到的频率值进行了比较，实验与理论结果吻合良好，实验结果令人满意。限于实验条件的限制，本文没有给出液面晃动振型的测量结果，在实验条件允许的情况下，仍可采用本文的方法，布置多个激光位移传感器同时测量液面的晃动，可容易获得液体自由表面的振型曲线。

致谢：本文工作得到了王庄博士的协助，特此致谢。

参 考 文 献

[1] Dodge F T.The New Dynamic Behavior of Liquids in Moving Containers[R].San Antonio, TX: Southwest Research Institute,2000.

[2] Ibrahim R A. Liquid sloshing dynamics: theory and applications[M].Cambridge: Cambridge University Press,2005.

[3] Faltinsen O M, Timokha A N. Sloshing[M].Cambridge: Cambridge University Press, 2009.

[4] 夏益霖.液体晃动等效力学模型的参数识别[J].应用力学学报,1991,8(4):27-35.

XIA Yi-lin. Parameters estimation for liquid sloshing equivalent mechanical models[J].Chinese Journal of Applied Mechanics,1991,8(4):27-35.

[5] 丁文镜,曾庆长.晃动液体单摆模型动力学参数的频域辨识[J].振动工程学报，1992,5(3):211-218.

DING Wen-jing, ZENG Qing-chang. Identification in frequency domain for dynamic parameters of pendulum model of sloshing liquid[J].Journal of Vibration Engineering,1992,5(3):211-218.

[6] 王为,夏恒新,李俊峰,等. 半球形容器中液体自由晃动非线性现象的实验研究[J].清华大学学报,2008, 48(11):1833-1836.

WANG Wei, XIA Heng-xin,LI Jun-feng,et al. Experimental investigation on the nonlinear phenomenon of liquid free sloshing in a hemisphere container[J].Journal of Tsinghua University,2008,48(11):1833-1836.

[7] Hasheminejad S M,Aghabeigi M. Liquid sloshing in half-full horizontal elliptical tanks[J]. Journal of Sound and Vibration,2009,324(1/2):332-349.

[8] Li Yu-chun, Wang Zhuang. An approximate analytical solution of sloshing frequencies for a liquid in various shape aqueducts[J].Shock and Vibration,2014:672648.

[9] 李遇春, 张皓. 二维晃动模态的统一Ritz计算格式[J].振动与冲击,2014，33(19)：85-89.

LI Yu-chun, ZHANG Hao. A unified Ritz algorithm for two-dimensional slosh modes[J].Journal of Vibration and Shock,2014,33(19): 85-89.

Experimental identification for the natural frequencies and damping ratios of two-dimensional sloshing

WANGLi-shi,LIYu-chun，ZHANGHao(College of Civil Engineering, Tongji University, Shanghai 200092, China)

Abstract:The modal parameters of sloshing fluid are essential to the design of liquid tanks and vibration control.In the modal experiment of fluid sloshing，the modal motions of free liquid surface should be excited.However, the symmetric-mode motions of free surface are difficultly stimulated, therefore the modal parameters (especially for the damping ratios) of the symmetric modes cannot be accurately measured.This paper applied parametric vibration method to excite two-dimensional (parametric) sloshing in rectangular, U-shaped and circular tanks.The first four mode motions (including the symmetric-mode motions) of free surface were easily aroused.After stopping the external excitation, a free damped-vibration response of a certain mode on the free liquid surface could be obtained with the laser displacement sensor.The sloshing natural frequencies and the corresponding damping ratios were precisely obtained.The experimental and theoretical frequency results agree well, which validates the present experimental method.

Key words:two-dimensional sloshing; parametric vibration; experiment; liquid; modal parameter

中图分类号:O353.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.027

通信作者李遇春 男，博士，教授，博士生导师，1962年2月生

收稿日期：2014-11-27修改稿收到日期：2015-04-21

基金项目：国家自然科学基金资助项目(51279133)

第一作者 王立时 男，博士生,1987年9月生