桥梁风障挡风性能的试验研究
2016-05-20杨庆山北京交通大学土木建筑工程学院北京00044结构风工程与城市风环境北京市重点实验室北京000444
李 波, 张 剑, 杨庆山(.北京交通大学 土木建筑工程学院,北京 00044; 2.结构风工程与城市风环境北京市重点实验室,北京 000444)
桥梁风障挡风性能的试验研究
李波1,2, 张剑1, 杨庆山1,2(1.北京交通大学 土木建筑工程学院,北京100044; 2.结构风工程与城市风环境北京市重点实验室,北京1000444)
摘要:通过测速风洞试验,得到了孔隙率、障条宽度对桥梁风障挡风性能的影响规律,并对桥梁风障的模拟方法及其挡风性能评价参数进行了研究。试验结果表明,风障有效挡风高度约为2.0H(H为风障高度),在1.0H范围内,风速降低较多,在1.0H高度处,流场湍流度达到最大。孔隙率对风障挡风性能影响较大,随着孔隙率的增大,风障下游风速增大,湍流度减小。障条宽度对风障挡风性能影响较小,相同孔隙率时,障条宽度对风障下游湍流度的影响可以忽略。按压力等效定义的风速折减系数较好反映了风速的变化规律,能够来用定量评价风障的挡风效果。
关键词:风障;挡风;桥梁;风洞试验;孔隙率;障条宽度
桥梁是现代交通运输系统中的重要组成部分,在国民经济与社会发展中占有极其重要的地位[1]。风是大跨度桥梁结构设计的主要控制性载荷,由于抗风设计不合理风致桥梁破坏事故屡见不鲜;另一方面,因高风速而禁止车辆通行更是影响桥梁运营的瓶颈问题,造成了巨大的经济损失[2-4]。经过数十年的不懈努力,桥梁风致振动理论已经逐步完善起来,千米跨度范围内的各类桥梁均有较为成熟的措施用来保证桥梁的抗风性能。因此,改善桥梁(特别是大跨桥梁)的使用功能越来越受到研究者和设计人员的关注。
桥梁风障是设置于桥梁两侧,用于降低风速、防止车辆侧翻,保证车辆在侧风作用下行车安全的桥梁附属结构。通过加设风障能够降低桥面风速、增加桥面行车舒适性、是改善桥梁使用功能的一种主要手段。一般情况,桥梁大多采用“钢立柱+障条”的条式风障(见图1),其中,立柱起支撑作用,障条起挡风作用,通过调节障条的宽度、间距以及数量控制风障的挡风效果。英国赛文桥、香港青马大桥、中国杭州湾大桥均是通过风障提高桥梁运行效率的成功案例[5- 7]。

图1 桥梁风障Fig.1 Wind barrieron the bridge
由于桥梁的安全是关注的焦点,已有研究往往是针对某个实际工程,采用数值模拟的方法分析风障的挡风性能,并未就桥梁风障的模拟方法及其对下游流场的影响进行专门研究[8-9]。基于上述情况,本文将采用风洞试验的方法,对上述问题进行研究,为进一步研究风障遮挡下的列车气动力特征提供参考。
1试验介绍
1.1试验模型及测试方法
本次试验在北京交通大学风洞实验室高速试验段完成,该风洞(见图2)为双试验段回流式闭口风洞,风洞洞体平面尺寸为41.0 m×18.8 m,其中,高速试验段尺寸为:3.0 m×2.0 m×15.0 m,低速试验段尺寸为:5.2 m×2.5 m×14.0 m。经第三方校核,风洞风场品质优秀。

图2 北京交通大学风洞试验室Fig.2 Wind tunnel laboratory in Beijing Jiaotong University
选取实际工程中最常采用的双向八车道、箱型主梁大跨度桥梁为研究对象(见图3),制作用于桥梁风障挡风性能研究的桥梁刚性节段模型,该模型与实际桥梁保持几何相似,几何缩尺比1∶75,模型参数如表1所示。模型制作完成后,通过连接件将模型固定到风洞高速试验段的外支架上,确保在试验过程中模型不发生振动[10-12]。安装完毕后,桥梁截断模型位于风洞横截面中间,有效避免了风洞底板边界层的影响。
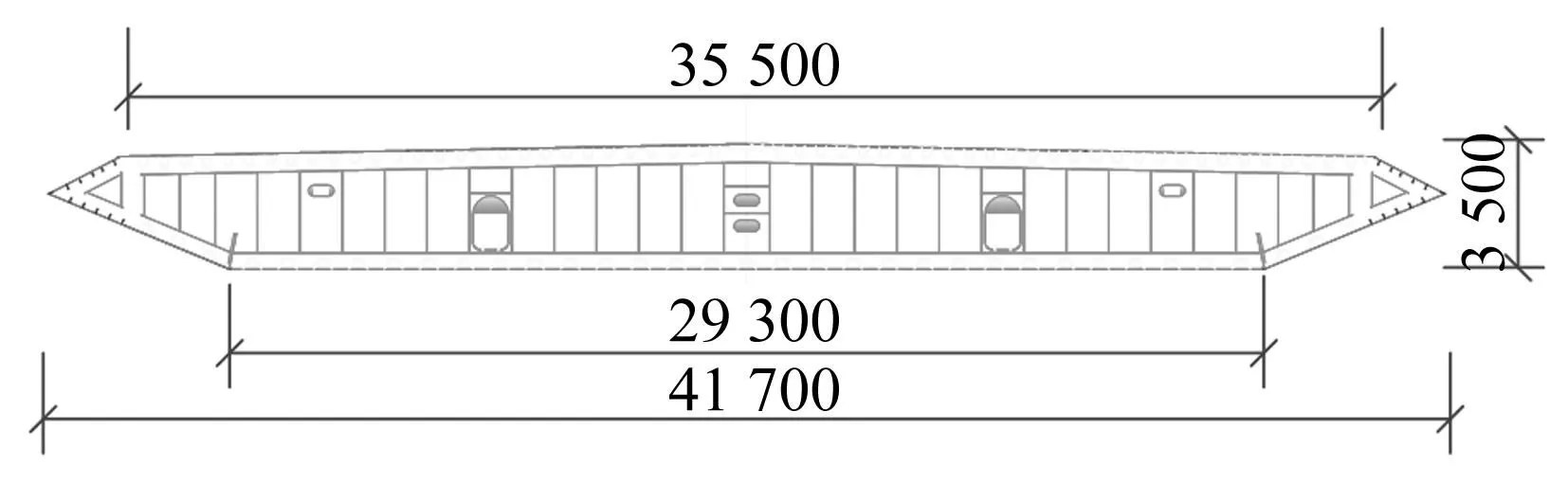
图3 桥梁主梁断面(mm)Fig.3 Cross section of bridge girder(mm)
为了方便测得桥面风场,采用间距为20 mm的钢针制作排管(顶部两排间距分别增大至40 mm和60 mm)。试验中将钢针与电子扫描阀相连,测得测点处动压,然后通过风速与风压的关系转化得到测点处的风速。为了验证排管的测量精度,在正式试验前,将排管安装在风洞地面上,测得风速沿高度分布,同时,通过皮托管测得相同高度处来流的风速值,两种方法测得的风速如表1所示。可以看出两种方法测量得到的风速误差小于3%,这说明排管能够用于桥面风场的测量。
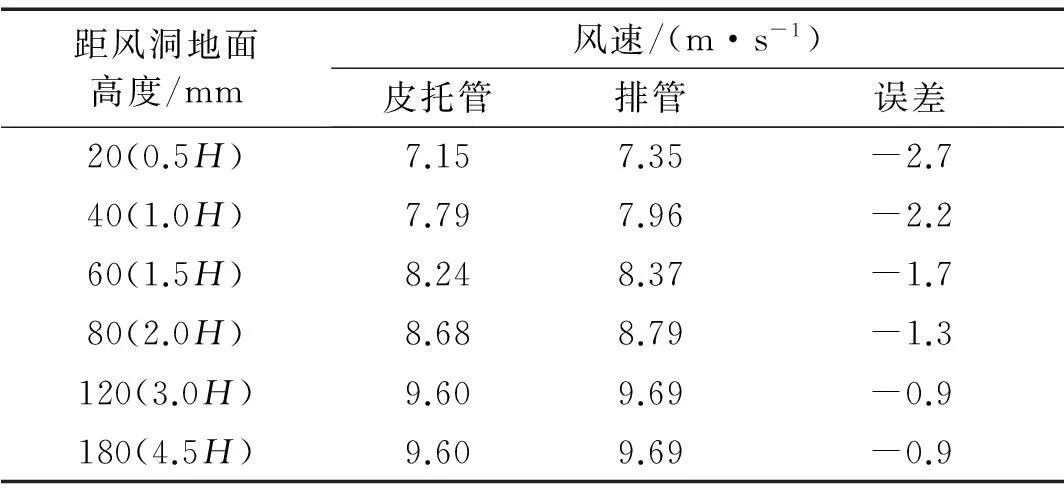
表1 风速测量结果
1.2试验工况与风障参数
风障高度虽然是影响其挡风效能的主要参数,但在实际工程中,风障高度一般是固定的。因此,本次试验中风障高度均3 m,主要研究风障孔隙率、所用障条宽度对其挡风性能的影响,试验工况及障条参数如表2所示。
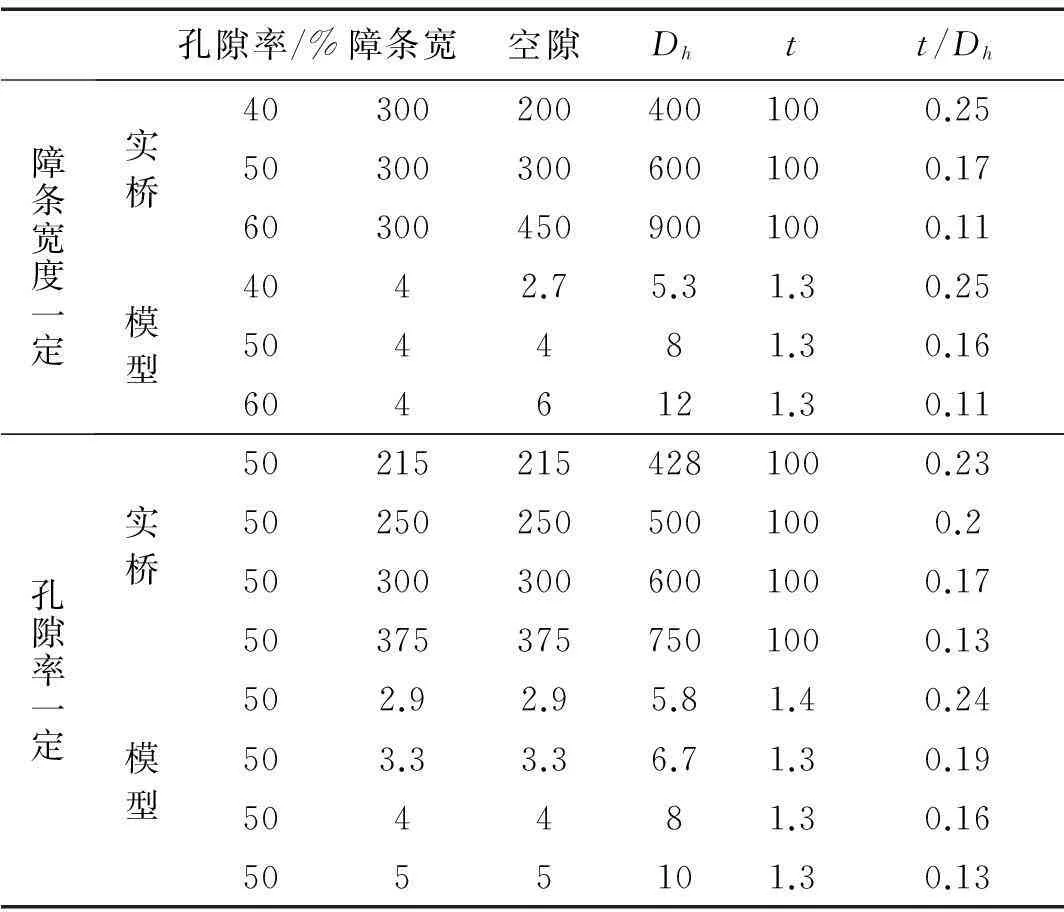
表2 风障参数
为了准确模拟开孔类物质的气动性能,除满足几何相似外,其缩尺模型与原型还需满足下面准则[13]:
1) 孔隙率ε相同
2) 板厚t与等效水力直径Dh之比相同
其中,气流流经障条式风障可近似为无限宽(宽度≫高度)的平行板间流动,其等效水力直径Dh取为2倍的板间距[14]。因此,为了满足上述准则需要选择合适的障条板厚度。根据试算,本次试验所用障条板厚取为1.3 mm,试验用风障如图4所示。

图4 风障模型图Fig.4 Wind barrier model
1.3有效性验证
Maruyama[15]通过风洞试验和数值模拟的方法对防风栅下游风场进行了研究,其中,所用到的试验装置如图5所示。该试验通过架空平台避免风洞底板边界层的影响,和本文采用的外支架抬高模型作用相同。
采用相同装置,图6给出了本文得到的60%孔隙率的风障下,距离风障3H处的平均风速剖面与Maruyama 测得的相同工况对比结果,图中,H表示风障高度,h表示测点距桥面高度,U表示来流平均风速,u表示测点处平均风速。可以看出,两者测量得到的无量纲风速比沿高度分布基本相同。

图5 风洞试验中的风障Fig.5 Arrangement of a wind breaks in wind tunnel
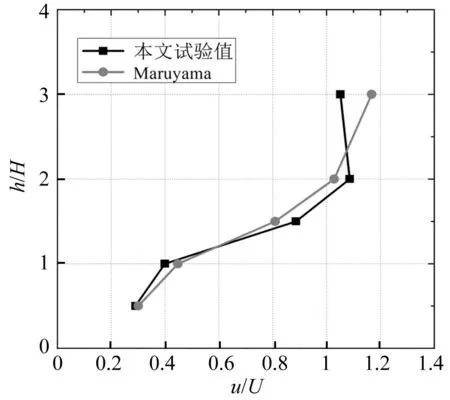
图6 风速比分布对比Fig.6 Comparison of distribution of ratio of wind velocity
2风障孔隙率的影响
本次风洞试验测试了障条宽度为300 mm,孔隙率分别为0%、40%、50%、60%、100%(即无风障)时,桥面风场的分布,根据风障下游平均风速的分布,说明风障孔隙率对其挡风性能的影响。
图7给出了第三车道无量纲风速比沿高度的分布。可以看出,不同孔隙率的风障都能起到一定的挡风作用。全封闭风障(孔隙率0%)对风速的遮挡影响高度最大,达到3H;设置一定孔隙率(40%~60%)后,风障对风速的影响高度降至2H。值得注意的是,当风障为全封闭时,在1.5H高度范围内,风速很小,且随着高度的增加,风速基本保持不变。但在该高度以上,风速随高度的增加而急剧增加,在3H高度处,风速增大至1.08U,相对于无风障状态,风速有所增大。
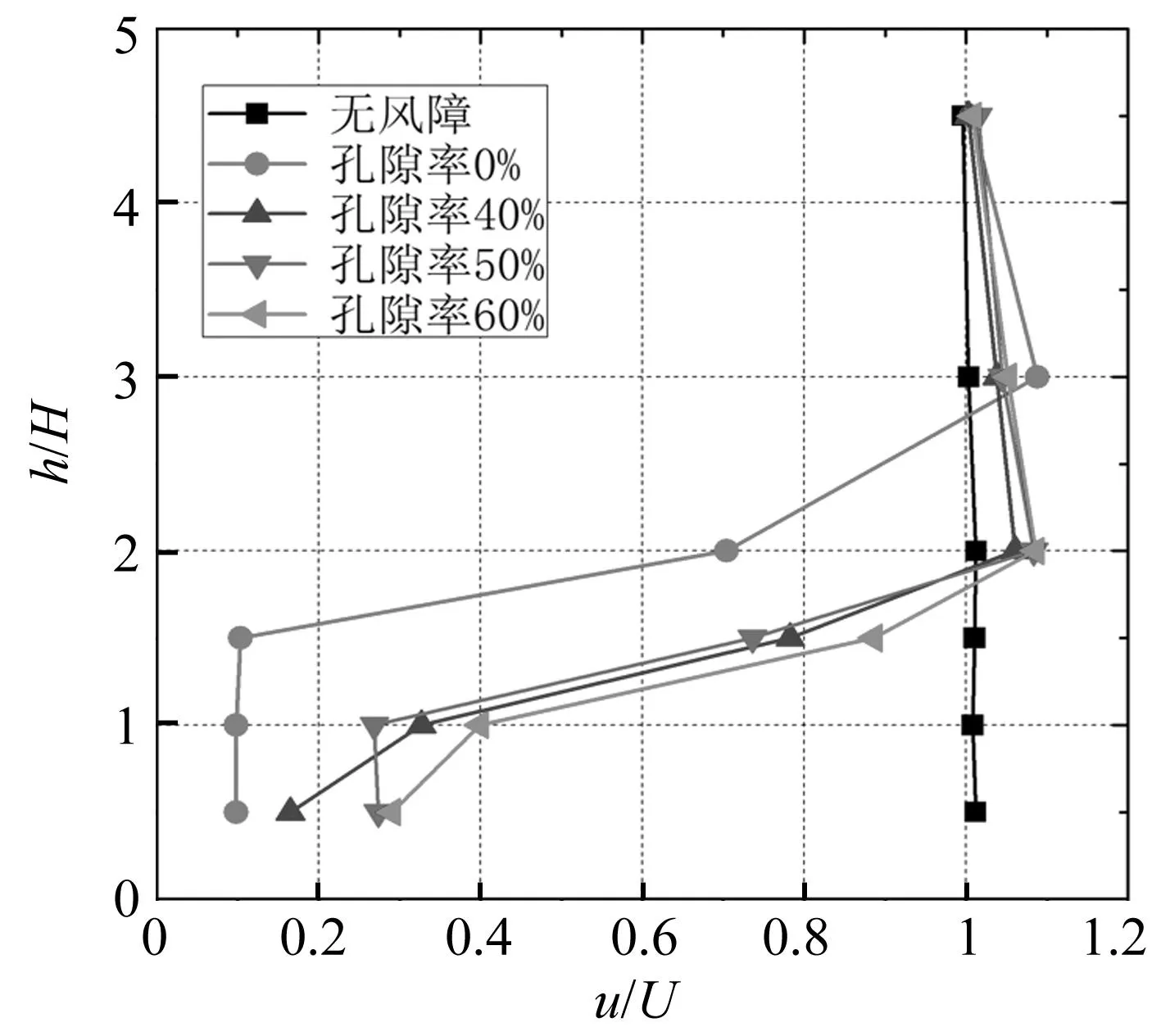
图7 风速比分布Fig.7 Distribution of ratio of wind velocity
参照轿车、中型卡车、集装箱车三种典型车辆的高度,分别取1H、1.5H、2H处的风速比,观察其在50%孔隙率的风障下风速沿车道横向分布,如图8所示。图中,纵轴表示相对风速,横轴x表示测点与风障的横向距离。
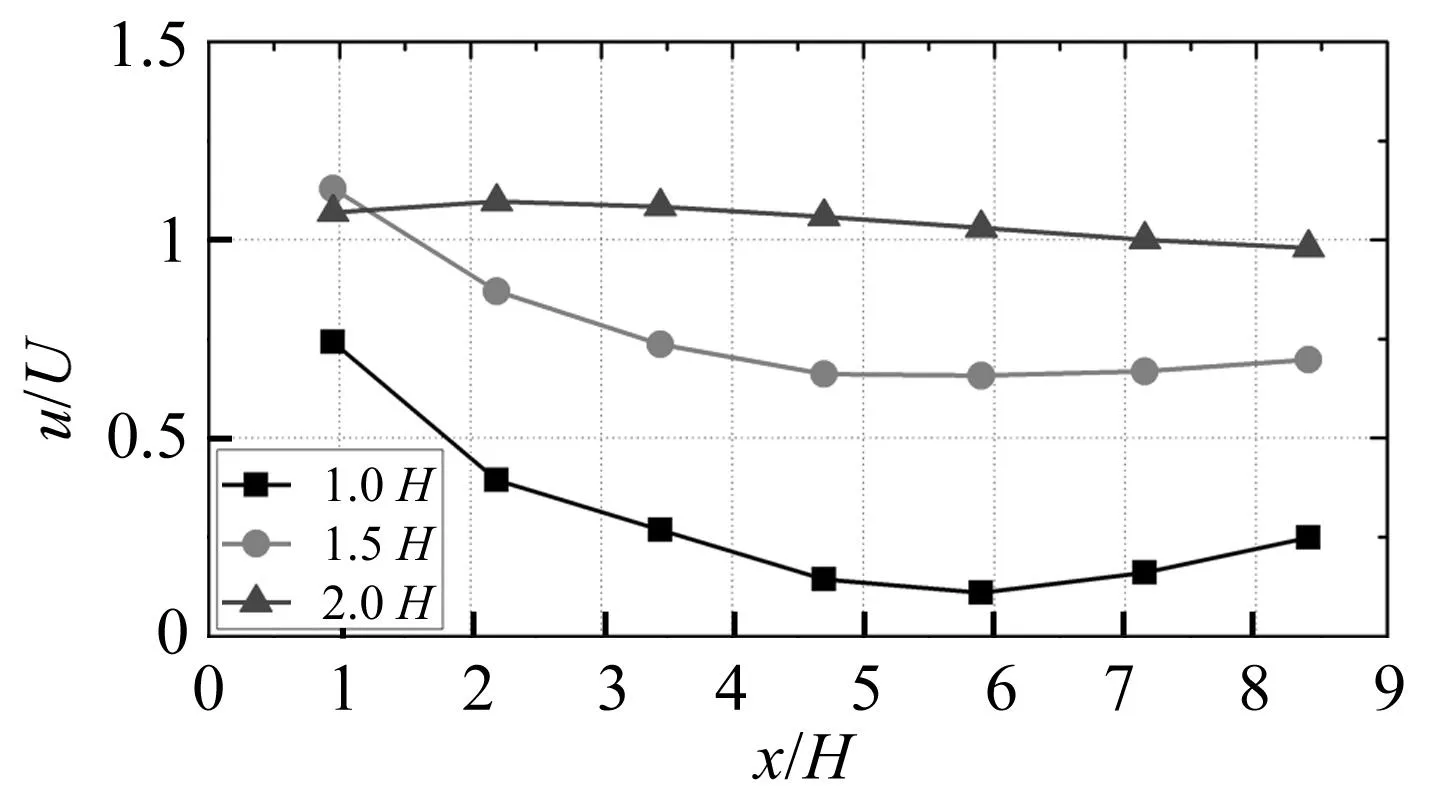
图8 风速比沿车道分布Fig.8 Distribution of relative wind velocity along the lane
可以看出,随着高度的增大,各个车道的风速也是逐渐增大的。在距离桥面2H处,风速沿纵向变化较小,且在下游车道处的风速基本接近来流风速,这说明,此时风速基本已不受风障的影响。不同高度处,风速沿桥面都是先降低后逐渐增大,风速在第五车道处达到了最小值。对于三类车辆而言,50%孔隙率的风障对轿车的挡风效果最好,且在第五车道处风速能够达到最小。
图9给出了不同高度处,8个车道最大风速比分布图。可以看出,对全桥而言,不同孔隙率风障的有效遮挡高度均为H,在该区域内,全封闭风障风速比能下降至0.25U,随着孔隙率的增加,有效遮挡区域内的风速逐渐增加。当孔隙率达到60%时,风速比增至0.82U。
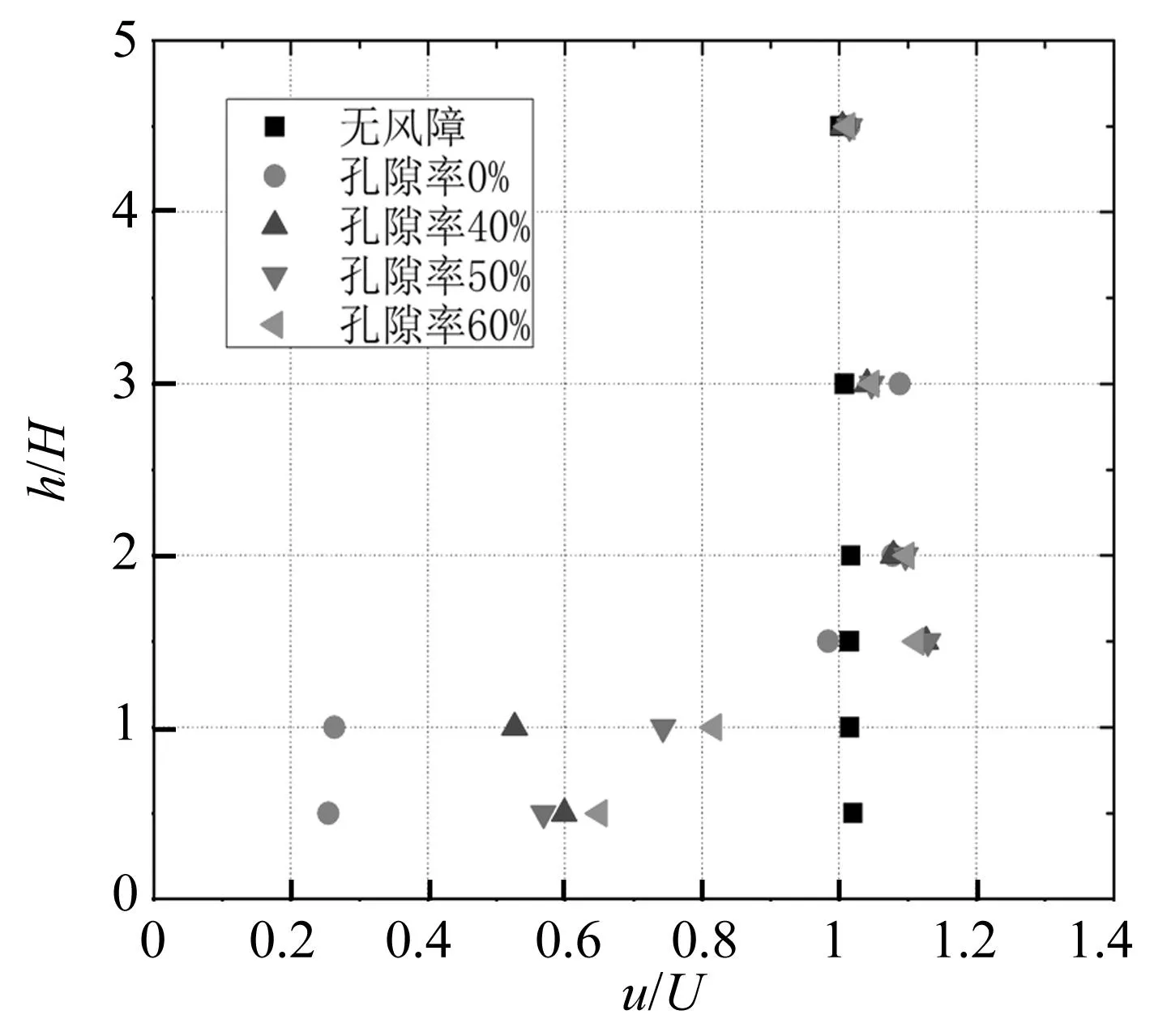
图9 风速比极值分布Fig.9 Distribution of the maximum of relative wind velocity
根据实际风速剖面可以计算出相应的等效风速,其计算原理是将实际风剖面等效为矩形,等效原则为实际风剖面和矩形风剖面的压力总和相等。定义无量纲化后的矩形等效风速为风速折减系数,可按下式进行计算:
(1)
式中,r为风速折减系数,hr表示所选风剖面高度,本文取3.0H,u(h)表示高度h处测得的风速。
表3给出了在不同孔隙率的风障遮挡下,一至五车道的风速折减系数。可以看出,风速折减系数较好反映了风速的变化规律,能够定量表示风障在不同位置处的挡风效果。

表3 风速折减系数分布
图10给出了第三车道湍流度沿高度的分布。可以看出,全封闭风障(孔隙率0%)对湍流度的影响高度最大,达到3H;设置一定孔隙率(40%~60%)后,湍流度影响高度降至2H,并且,随着孔隙率的增大,湍流度变小。值得注意的是,不同孔隙的风障,湍流度都在1H高度达到最大。
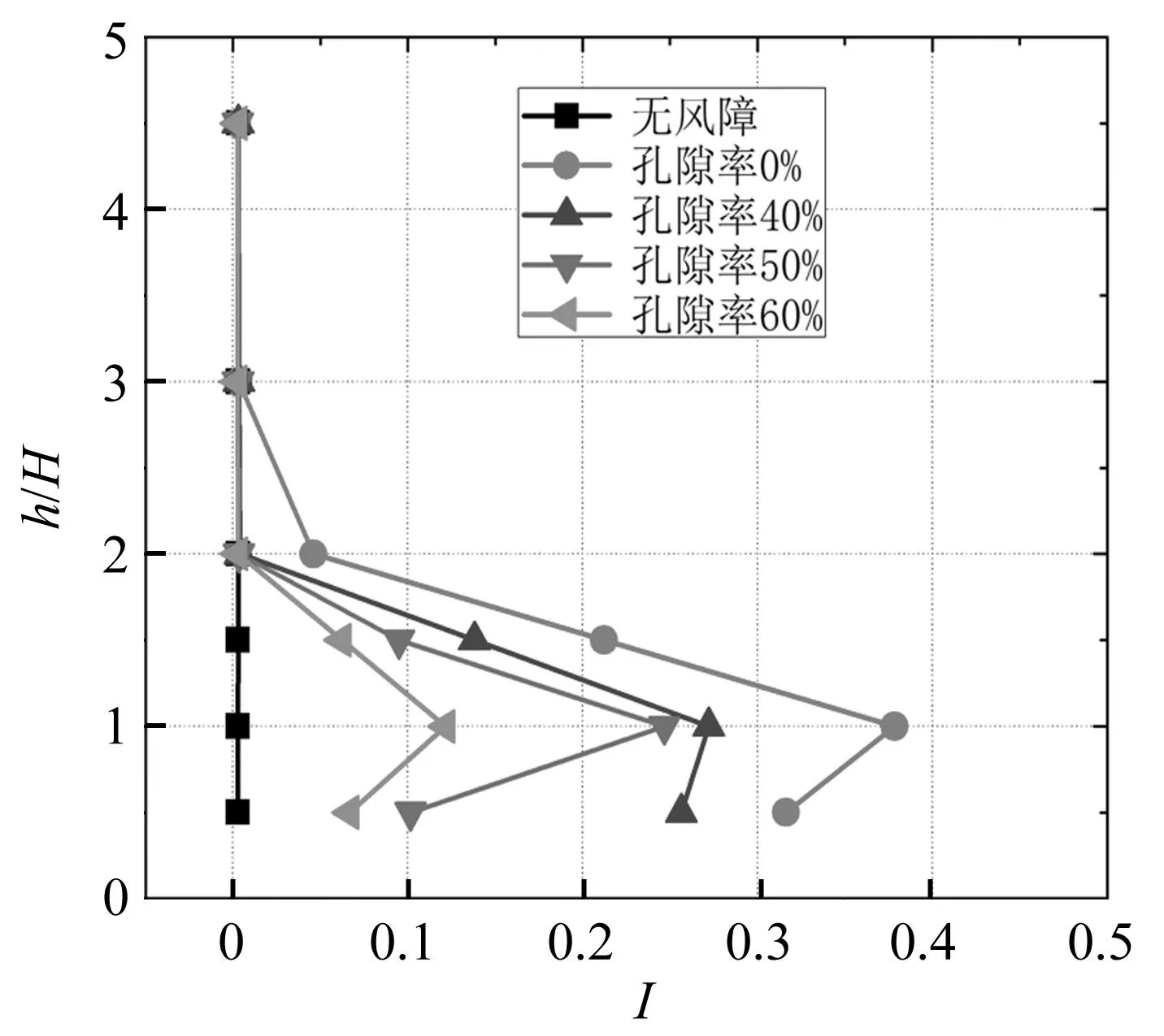
图10 湍流度分布Fig.10 Distribution of Turbulence Intensity
图11给出了不同高度处,8个车道最大湍流度分布图。可以看出,对全桥而言,湍流度也是在1H高度处达到最大。同样高度处,湍流度大致随着孔隙率的增大而减小。
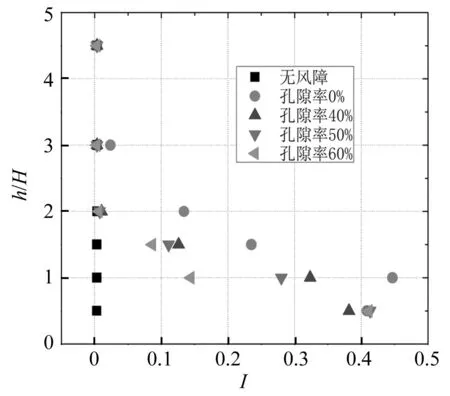
图11 湍流度极值分布Fig.11 Distribution of the maximum of turbulence intensity
3风障障条宽度的影响
图12给出了风障孔隙率为50%,不同障条宽度时,第三车道无量纲风速比沿高度的分布。
可以看出,风速在1H高度范围内有一定差异,但在该高度以上,各工况时测得的风速基本相同。这说明,相同孔隙率时,障条宽度对风障挡风效率的影响不大。
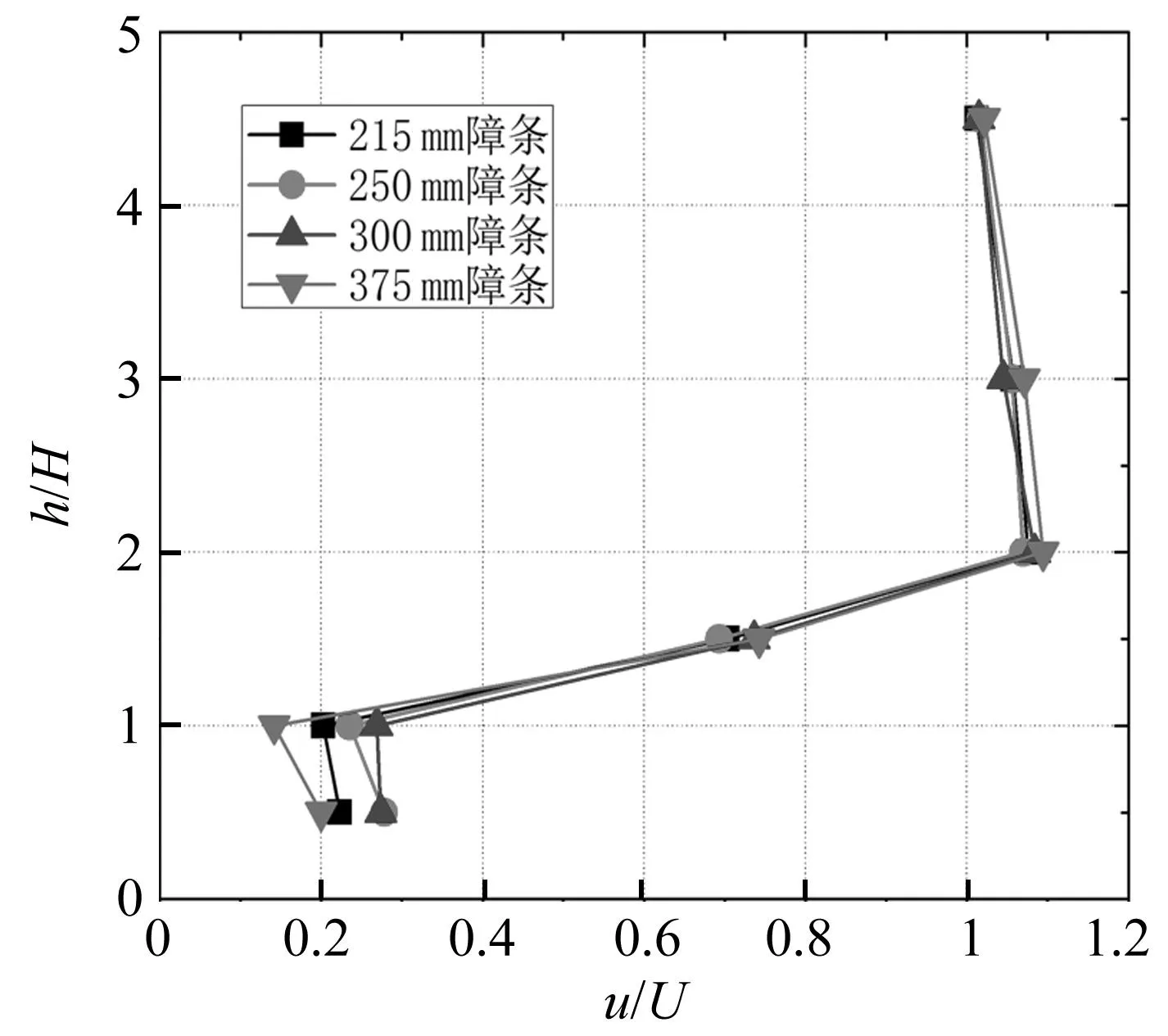
图12 风速比分布Fig.12 Distribution of ratio of wind velocity
图13给出了在不同障条宽度时,第三车道湍流度沿高度的分布。
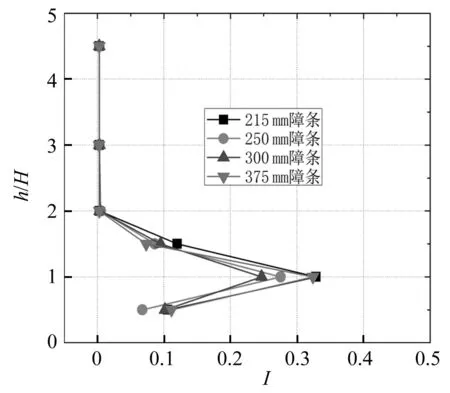
图13 湍流度分布Fig.13 Distribution of turbulence intensity
可以看出,孔隙率相同时,仅在1H高度处,障条宽度对湍流度有一定影响,其它位置处,障条宽度对湍流度的影响也不大。这说明,相同孔隙率时,障条宽度对风障下游湍流度的影响可以忽略。
4结论
本文通过风洞试验,研究了风障孔隙率以及障条宽度对桥面风速、湍流度的影响。主要结论如下:
(1) 在风洞模拟风障的挡风性能时,除几何尺度相似外,风障的孔隙率、厚度也要按要求进行相似比设计。
(2) 孔隙率对桥梁风障的挡风性能影响较大,障条宽度影响较小。随着孔隙率的增大,风障下游风速增大,湍流度减小。
(3) 风障有效挡风高度约为2.0H(H为风障高度),在1.0H范围内,风速降低较多,但在1.0H高度处,流场湍流度达到最大。
(4) 按压力等效定义的风速折减系数能够用来定量评价风障的挡风效果。
参 考 文 献
[ 1 ] 项海帆, 林志兴.公路桥梁抗风设计指南[M].北京:人民交通出版社, 1996.
[ 2 ] 刘庆宽, 杜彦良.日本列车横风和强风对策[J].铁道学报,2008, 30(1): 82-88.
LIU Qing-kuan, DU Yan-liang.Train-crosswind and strong wind countermeasure research in Japan[J].Journal of the China Railway Society, 2008, 30(1):82-88.
[ 3 ] Smith B W, Barker C P.Design of wind screens to bridges: experience and applications on major bridges[J].Bridges Aerodynamics,1998,3:289-298.
[ 4 ] 金学松, 郭俊, 肖新标.高速列车安全运行研究的关键科学问题[J].工程力学, 2009, 26(增刊Ⅱ):8-22.
JIN Xue-song, GUO Jun, XIAO Xin-biao.Key scientitfic problems in the study on running safety of high speed trains[J].Engineering Mechanics, 2009, 26(SupⅡ): 8-22.
[ 5 ] 周奇, 朱乐东, 郭振山.曲线风障对桥面风环境影响的数值模拟[J].武汉理工大学学报,2010, 32(10): 38-44.
ZHOU Qi, ZHU Le-dong, GUO Zhen-shan.Numerical simulation for curve windshield barrier effects on wind environment around bridge deck[J].Journal of Wuhan University of Technology,2010, 32(10): 38-44.
[ 6 ] 阮欣, 陈艾荣, 王达磊.杭州湾跨海大桥风障设置风险评估[J].桥梁建设, 2007(1):78-84.
RUAN Xin, CHEN Ai-rong, WANG Da-lei.Risk assessment of installing of wind shielding screen for Hangzhou Bay Sea-crossing Bridge[J].Bridge Construction, 2007(1):78-84.
[ 7 ] Chu C R, Chang C Y. Windbreak protection for road vehicles against crosswind[J].Journal of Wind Engineering and Industrial Aerodynamics,2013,116:61-69.
[ 8 ] 丛晓春, 张旭.风障外流场风速分布的预测[J].同济大学学报,2004,32(1):31-35.
CONG Xiao-chun, ZHANG Xu.Numerical prediction of airflow around windbreak[J].Journal of Tongji University, 2004,32(1):31-35.
[ 9 ] 董香婷, 党向鹏.风障对侧风作用下列车行车安全影响的数值模拟研究[J].铁道学报, 2008,30(5): 36-41.
DONG Xiang-ting, DANG Xiang-peng.Train-crosswind and strong wind countermeasure research in Japan[J].Journal of the China Railway Society, 2008, 30(5): 36-41.
[10] 张健.铁路防风栅抗风性能风洞试验研究与分析[J].铁道科学与工程学报, 2007, 4(1): 13-17.ZHANG Jian.Wind-tunnel test investigations and analysis on wind break performances of wind fences on railway[J].Journal of Railway Science and Engineering, 2007, 4(1): 13-17.
[11] 向活跃, 李永乐, 胡喆.铁路风屏障对轨道上方风压分布影响的风洞试验研究[J].实验流体力学, 2012,26(6):19-23.XIANG Huo-yue, LI Yong-le, HU Zhe.Effects of wind screen on wind pressure distribution above railway tracks by wind tunnel test[J].Journal of Experiments in Fluid Mechanics,2012,26(6):19-23.
[12] 王达磊, 陈艾荣, 马如进.风障对桥塔附近桥面汽车气动力特性的影响[J].工程力学,2013, 30(10): 244-250.
WANG Da-lei, CHEN Ai-rong, MA Ru-jin.Influence of wind barrier on aerodynamic characteristics of automobiles on bridge girder near pylon[J].Engineering Mechanics, 2013, 30(10): 244-250.
[13] Allori D, Bartoli G, Mannini C.Wind tunnel tests on macro-porous structural elements:a scaling procedure[J].Journal of Wind Engineering and Industrial Aerodynamics,2013,123(1):291-299.
[14] 周雪漪.计算水力学[M].北京:清华大学出版社,1995.
[15] Maruyama T.Large eddy simulation of turbulent flow around a windbreak[J].Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10/11): 1998-2006.
Experimental study on windbreak performance of wind barriers on bridge
LIBo1,2,ZHANGJian1,YANGQing-shan1,2(1.School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China; 2.Beijing’s Key Laboratory of Structural Wind Engineering and Urban Wind Environment, Beijing 100044, China)
Abstract:Wind tunnel velocity tests have been carried out to investigate the windbreak performance of wind barriers on bridges considering different barrier porosities and widths, the wind barrier wind tunnel simulation method and evaluation parameter of windbreak performances are discussed in the paper.Test results show that the shielding region of wind barriers is about 2.0H (H is the height of wind barrier) and that wind speed decreases significantly when the height is below 1.0H.The turbulence intensity of the downstream flow on the wind barrier reaches the maximum at a height of 1.0H.Windbreak performance depends on porosity of wind barrier, wind speed will rise and turbulence intensity decreases with increasing porosity.Barrier width seems to have no relationship with windbreak performance; when porosity is the same, the effect of barrier width can be ignored.The wind speed reduction coefficient can be used to evaluate windbreak performance, which is defined by pressure equivalence.
Key words:wind barrier; windbreak; bridge; wind tunnel test; porosity; width of barrier
中图分类号:TU973.212
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.08.013
收稿日期:2015-09-29修改稿收到日期:2015-11-05
基金项目:国家自然科学基金项目(51378060);高等学校学科创新引智计划(B13002)
第一作者 李波 男,博士,副教授,1978年生
E-mail:libo_77@163.com
