基于本征方程求解复合材料梁几何非线性静力平衡

李园园， 何　欢， 陈国平， 刘庞轮(南京航空航天大学 机械结构力学及控制国家重点实验室，南京　210016)



基于本征方程求解复合材料梁几何非线性静力平衡

李园园， 何欢， 陈国平， 刘庞轮(南京航空航天大学 机械结构力学及控制国家重点实验室，南京210016)

摘要：对基于本征梁理论求解复合材料梁的几何非线性大变形屈曲问题进行了研究，根据材料属性利用渐近变分法确定复合材料梁的刚度矩阵，再根据本构方程和平衡方程求得其静力学行为，结果表明：对单层铺层的复合材料梁来说，刚度矩阵的耦合项可以忽略，其变形构型及梁末端的位移及转角的变化趋势与各项同性材料相同；对一个一般的复合材料梁来说，其刚度矩阵的耦合项不可忽略，耦合项对位移和转角的影响与施加在梁上的载荷大小有关，在载荷小于30 N，以耦合项50%的变化量为界，当变化量小于50%时，位移和转角的变化趋势与初始时相同，当变化量大于50%时，位移和转角的变化趋势发生很大的改变，但与解耦后的变化趋势相似。

关键词：本征梁理论；复合材料梁；渐近变分法；几何非线性；大变形；屈曲

在飞行器、运载火箭、人造卫星等的航空航天领域，以弹性体为主装配部件的大范围运动装置比比皆是。随着国民经济的高速发展，各种机械系统在向着构型复杂化，结构轻巧化，运转高速化方向发展，所有的这些要求导致系统部件要有较大的柔性，因此，空间大范围运动柔性结构的研究成为一个引人注目的话题，其基础结构包括梁，板，壳等。

梁作为一种常见的单元应用于不同的机械和结构单元中，它在航空工业中的典型应用是大展弦比机翼和直升机旋翼，在分析梁的大范围运动时，由于变形过程的复杂性，单纯的线性理论已不足以描述这种复杂的运动，而非线性变形的量化开始倍受关注，很多学者对其进行了研究。Christensen等[1-2]从应变与位移的非线性角度出发，Boutaghou等[3]则采用Hamilton原理，各自建立了柔性梁的非线性力学模型，Hodges[4]基于几何精确的本征梁理论，它采用线应变和角应变代替位移和转角作为独立变量。Gatti-Bono等[5]在不考虑剪切变形的情况下得到了和文献[4]类似的方程。冯志华[6]基于Kane方程的建模方法研究了大范围运动柔性梁的非线性行为。齐朝晖[7]运用虚功原理推倒了大变形梁的动力学公式，并给出线弹性材料的本构关系。利用上述学者建立的模型求解梁的动力学或静力学行为时，基本都是基于能量法和有限元法，这些方法一般都需要多次迭代，且随着几何的变形，有限元方法必须不断修正载荷和刚度矩阵，增加了计算的费用和仿真时间。

由于梁可以被看成是维数降阶的结构，以其轴线方向x1作为参考，其他所有量都可以表达为x1的函数，因此梁的非线性方程中只有一个独立变量，而迭代打靶法就是针对只有一个独立变量的边界值问题的数值求解方法[8]，后来，Shvartsman[9-11]提出了一种求解受伴随载荷的平面悬臂梁问题的直接打靶方法，这些方法求解的非线性方程组阶数较低，但它仍需要多次迭代，计算量较大，且直接打靶法局限于利用Euler-Bernoulli梁理论，不能推广到三维的情况。

为克服上述的计算困难，Karlson等[12]提出了基于本征梁方程的打靶法，用于计算三维空间内，具有预弯曲型梁的大变形平衡问题。对于受非保守载荷的悬臂梁边界值问题，该方法不需要迭代就能得到一个精确解。同时，这些方程是以1阶形式定义的，因此仅需要一个初始条件就可以计算。

本文基于文献[12]的建模和求解方法，结合Hodges提出的渐近变分法[13-16](Variational-Asymptotic Beam Sectional Analysis，VABS)求解了复合材料梁的几何非线性大变形问题，比较了复合材料梁与各项同性材料梁的变形构型及末端的位移和转角的变化趋势，同时探讨了某种复合材料梁的耦合项对变形构型及末端位移和转角的影响，为后续进一步研究提供新的思路和理论依据。

1本征梁方程

1.1运动学方程

如图1描述了一个长度为l的复合材料梁的变形过程，可用三个构型来描述：参考构型Ωref，初始构型Ω0和变形构型Ωf，其中，参考构型表示没有预弯曲的直梁，而初始构型存在预弯曲γ0和κ0，变形构型是用内力表示的应力状态下的构型，此时的线应变和角应变相对于参考构型分别表示为γf和κf。在上述三种构型中分别定义三组基：[I1,I2,I3]T，[b1,b2,b3]T和[B1,B2,B3]T，这三组基在各自的构型中是互相正交的，且[B1,B2,B3]T随着参考轴线坐标的变化而变化，b1=b2×b3，B1=B2×B3，其中，b1和梁的参考轴线x1相切，而由于剪切变形的存在，B1不一定相切于参考轴线s，参考轴线由x1变为s的位移向量表示为u(x1,t)。变形构型的基与参考构型的基(笛卡尔坐标系)之间有关系：Βi=BixI1+BiyI2+BizI3，其中，i=1,2,3，Bix,Biy,Biz表示Bi在笛卡尔坐标系下的坐标分量，初始构型的基与参考构型的基之间也存在类似的关系。由图1可以看出，梁从构型Ω0变化到构型Ωf后横截面发生翘曲，其中的虚线表示初始构型的横截面形状，阴影表示翘曲了的横截面形状，横截面翘曲后存在翘曲位移。

根据文献[14]，在初始构型Ω0中，沿参考轴线x1的任意一点处，梁中心线的位置向量r与横截面上任意一点的位置向量r*以及基坐标之间存在如下的关系：

r*(x1,x2,x3)=r(x1)+xαbα

(1)

式中,α=2,3，x2,x3是在横截面上与x1正交的单位矢量且初始时分别相切于b2,b3。

在Ωf处，梁中心线的位置向量R与横截面上任意一点的位置向量R*以及基坐标和翘曲位移之间存在如下的关系：

R*(x1,x2,x3)=R(x1)+xαBα(x1)+wiBi(x1)=

r(x1)+u(x1,t)+xαBα(x1)+wiBi(x1)

(2)

式中，wi是与x1,x2,x3有关的翘曲矢量。

根据文献[12]，在变形构型Ωf中，中心线位置向量R和基矢量以及线应变和弯曲变形之间存在如下的关系式：

R′j=(1+γ11)B1j+2γ12B2j+2γ13B3j

(3)

B′ij=κ×Bij

(4)

(5)

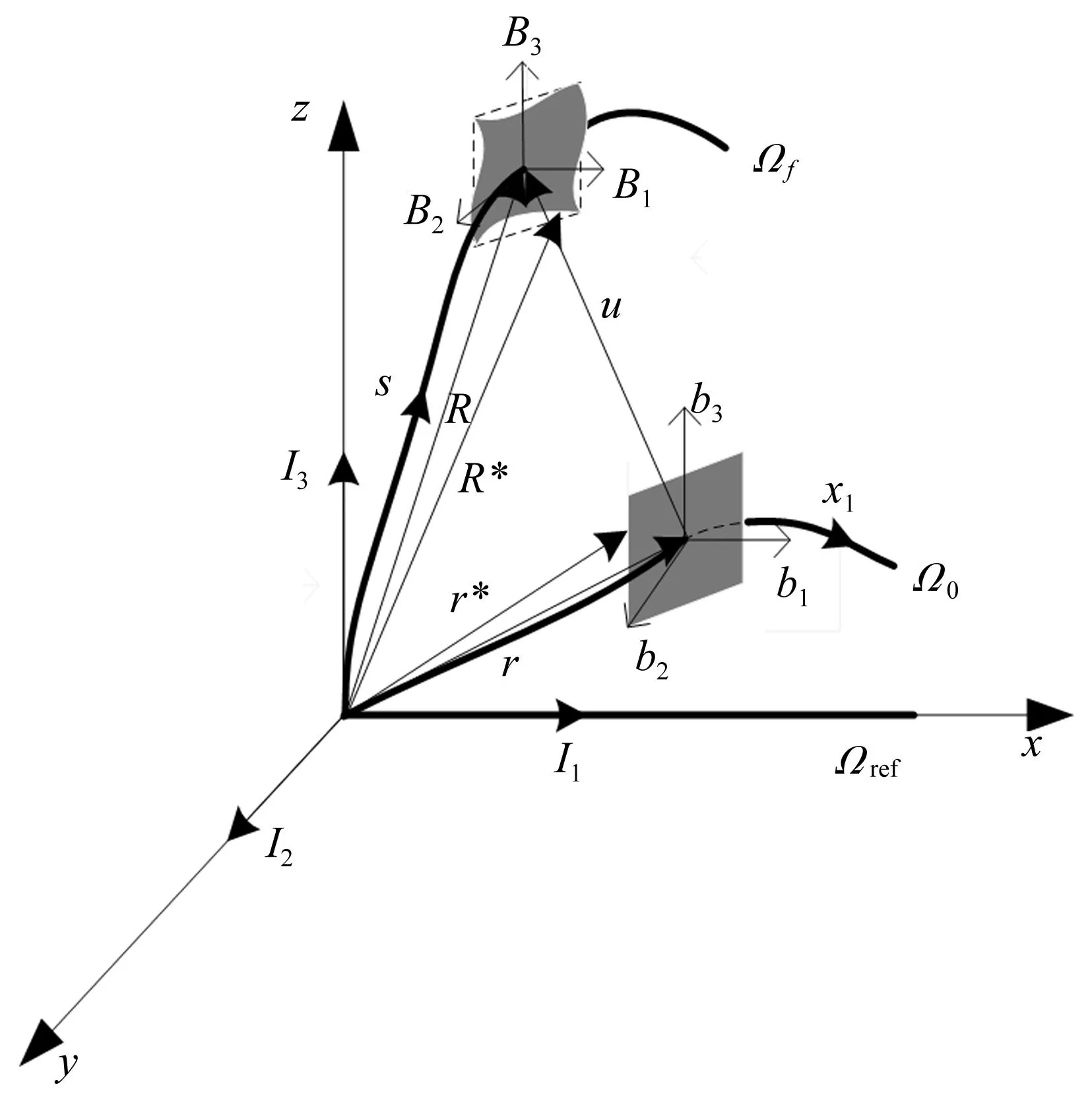
图1　梁的变形简图Fig.1 Schematic of beam deformation

1.2平衡方程

文献[17]提出的矩阵形式的运动方程定义了梁的线速度、角速度、弯曲应变及线应变的空间和时间变化，如式(6)和(7)：

(6)

M′+κf×M+(e1+γf)×F+m=

(7)

式中，上标“·”表示关于时间t的偏导数，内力F=[F1,F2,F3]T；弯矩M=[M1,M2,M3]T；单位长度上的外力和外力偶f=[f1,f2,f3]T和m=[m1,m2,m3]T；对应于线速度V=[V1,V2,V3]T和角速度Ω=[Ω1,Ω2,Ω3]T的单位长度线动量和角动量P=[p1,p2,p3]T和H=[H1,H2,H3]T；e1表示B1方向的单位矢量[1,0,0]T，γf=[γ11,2γ12,2γ13]T。

略去运动方程式(6)和(7)中的时间项与时间导数项，得到平衡方程式(8)和(9)：

F′+κf×F+f=0

(8)

M′+κf×M+(e1+γf)×F+m=0

(9)

内力和弯矩与弯曲变形和应变的本构方程式如下[18]：

(10)

其中，

(11)

为刚度矩阵，Sij(i=1,2,3,4,5,6，j=1,2,3,4,5,6)表示横截面的刚度系数，且SijT=Sji(i≠j)，下标1代表拉伸，2、3代表剪切， 4代表扭转，5、6代表弯曲。

对应变很小的各项同性材料梁，本构方程式(10)是线性的，此时的刚度矩阵D只存在对角线项，耦合项忽略不计，该刚度矩阵利用材料属性通过维数降阶即可获得[12]。然而，对初始弯曲变形不足够小的各项同性材料或对各项异性材料来说，刚度矩阵中的某些非对角线元素不能省略，这些非对角元素为耦合项，此时的刚度矩阵已不能通过简单的维数降阶获得。

注意到，在忽略剪切变形的情况下，式(10)得到弯曲变形和弯矩的关系：

(12)

其中，

(13)

2刚度矩阵的求解-渐近变分法(VABS)

前面提到，对初始弯曲变形不足够小的各项同性材料或对各项异性材料来说，刚度矩阵D不能通过简单的维数降阶获得，Hodges等开始将渐近变分法应用于求解复合材料梁的横截面弹性常数和翘曲场。对于梁这种维数降阶的结构，VABS是强有力的工具，它可以将一个一般的三维非线性弹性问题的求解转化为二维的线性横截面分析和一维的非线性分析两部分。经过不断发展，该方法已形成单独的工程软件包来进行具有任意横截面形状的各向异性材料梁的2D横截面分析。

在用渐近变分法求解横截面弹性常数时，所依据的基本理论是能量法，使容易求解的一维应变能近似代替原三维梁的应变能。式(14)给出了Timoshenko梁(1D)单位长度的能量与弹性常数和应变之间的关系[13]：

2U=εTXε+2εTYγs+γsTGγs

(14)

式中，ε=[γ11,κ1,κ2,κ3]T，分别代表广义应变(1D)中的拉伸，扭转和两个弯曲，γs=[2γ12,2γ13]T，X,Y,G即为组成6×6的刚度矩阵D的子矩阵。

式(14)可以转化为本构方程的如下形式：

{FM}=[Ds]{s}

(15)

式中，{FM}={F1M1M2M3F2F3}T，[Ds]=[XY;YTG]，{s}={εγs}T。

为求得X,Y,G，需将基于二阶渐进理论的梁横截面上的能量转化为1D的Timoshenko梁形式，转化过程涉及1D的动力学方程、本构方程和静力学平衡方程。基于二阶渐进理论的梁横截面上的应变能如下[15]：

(16)

将式(8)和(9)中所有的外力置为零，整理得到梁的静力学平衡方程变为如下形式：

{FM}′+[DM]{FM}=0

(18)

(19)

式中,R,S,T为横截面柔度矩阵的子矩阵。由式(19)递推得到：

(20)

将式(19)和(20)代入式(16)中，并使整理后的方程与式(14)对应，根据等号两边对应项相等即可求得X,Y,G的表达式，即确定了刚度矩阵。

3打靶法

对于受伴随力作用的悬臂梁来说，“打靶”从梁的自由端开始，一次“打靶”就能确定梁的非线性变形，不需要迭代，打靶过程自动实施了梁末端的固定边界。基于本征方程的打靶法就是将式(3)，(4)，(5)，(8)和(9)利用式(10)和(11)展开为具有初值问题的如下形式：

y′(x1)=f(x1,y(x1))

(21)

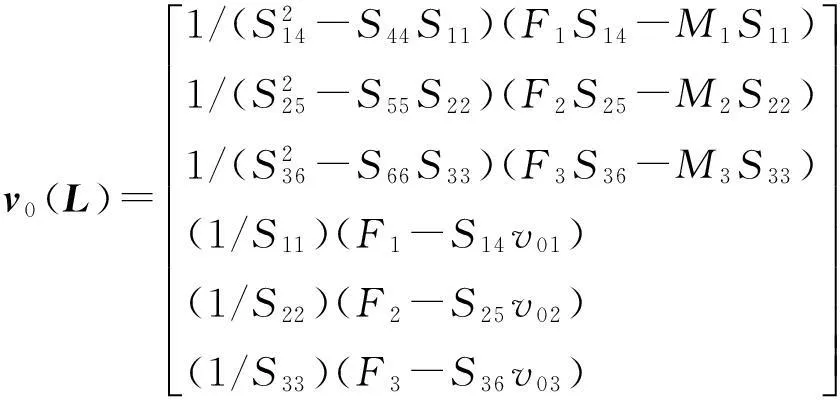
[uvw]T=R

(23)

式中，u，v，w分别对应全局坐标系下的X，Y，Z方向的位移。

基于上述理论，图2给出了本文基于本征方程求解复合材料梁的静力学问题的流程图。

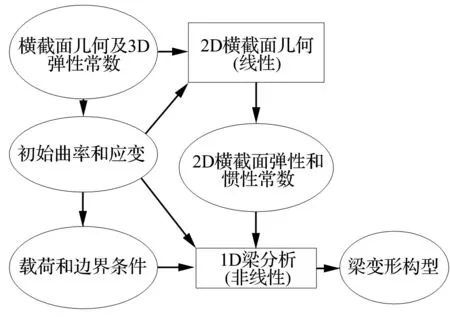
图2　复合材料梁静力学分析的流程图Fig.2 Flow chart of the static anlysis for composite beams

4算例

4.1算例1

算例1在忽略剪切变形，没有预弯曲的情况下，给出了末端分别承受不同大小单点力和分布力的各向异性材料直梁的变形构型、梁末端位移及转角的变化，并与文献[12]中承受单点力和分布力的各项同性材料直梁的变形构型、梁末端的位移及转角变化进行了对比。

表1给出了铺层只有一层的正交各向异性材料梁的材料属性、尺寸以及VABS输出的弹性常数，需要指出的是，表1给出的数值是在文献[20]的基础上进行单位换算得到的。其中，梁的长度是任意的，只要比横截面尺寸大的多即可。

其中，宽度方向沿横截面的x2，厚度方向沿横截面的x3，梁的长度L在本算中例取0.53 m，μ为梁单位长度的质量，i2,i3为横截面质量惯性矩，由表1发现，单层铺层的各向异性材料的刚度矩阵为对角阵，耦合项很小忽略不计。

表1　材料属性、横截面维数以及弹性常数

图3和图5分别为末端受不同大小单点力和分布力的各向异性材料直梁的变形构型，图4和图6分别为对应的梁末端位移及梁末端关于Y轴转角的变化趋势。

对比图3～图6以及文献[12]发现：对铺层只有一层的正交各向异性材料梁，其刚度矩阵耦合项很小以致忽略不计，只存在对角线元素，其变形构型、梁末端位移及转角的变化趋势与各项同性材料梁相同。

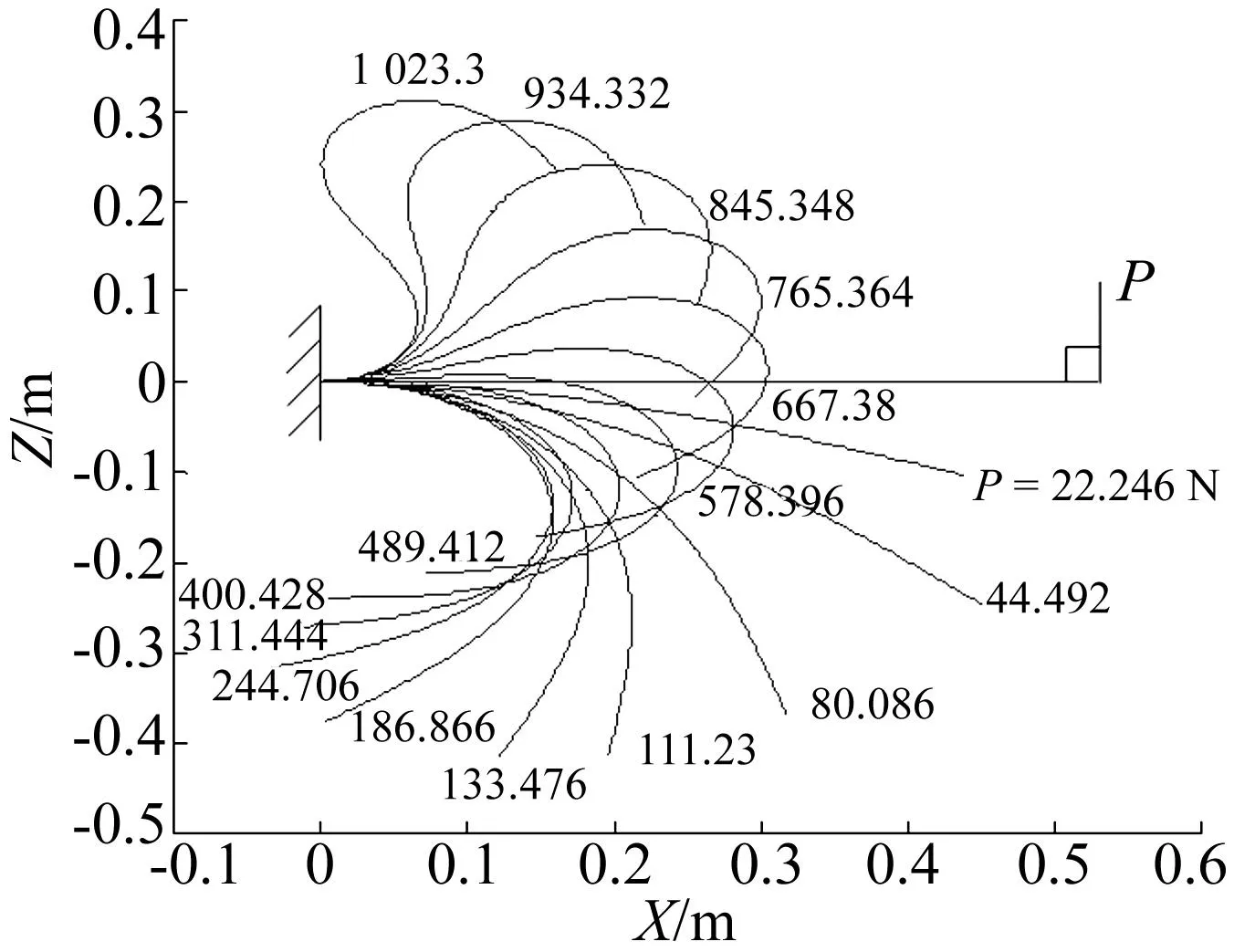
图3　受垂直梁末端单点伴随力作用的变形构型Fig.3 Deformation configuration of the beam loaded with a perpendicular, point, follower force

图4　单点力作用下的位移及转角Fig.4 Normalized displacements and rotations under perpendicular, point, follower force

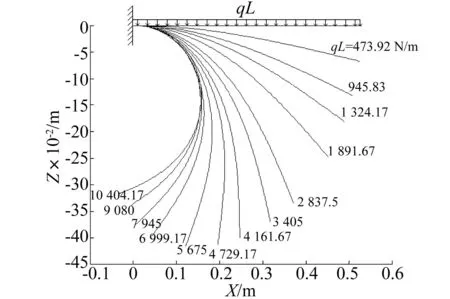
图5　受垂直梁均布伴随载荷作用的变形构型Fig.5 Deformation configuration of a straight beam loaded with a perpendicular, distributed, follower force

图6　均布载荷作用下的位移及转角Fig.6 Normalized displacements and rotations under perpendicular, distributed, follower force

4.2算例2

该算例同样在没有剪切变形及预弯曲的情况下，针对刚度矩阵耦合项不可忽略的各项异性材料梁，当末端承受不同大小的单点力时，观察梁末端位移及转角受耦合项的影响。表2给出了该各向异性材料梁的材料属性，横截面维数以及弹性常数。需要指出的是，表2给出的数值是在文献[21]的基础上进行单位换算得到的。

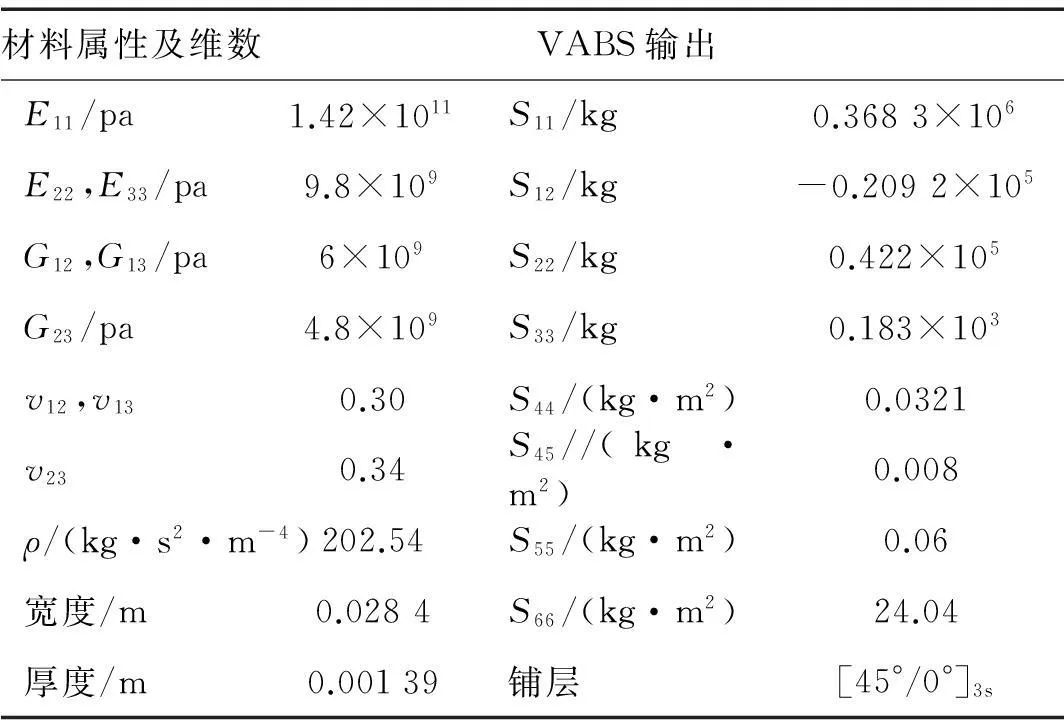
表2　材料属性、横截面维数以及弹性常数

为便于计算，该梁的长度L仍取0.53 m,由表2可以看出，该材料的拉-剪、弯-扭耦合S12,S45不可忽略。图7～图9分别给出了复合材料梁在单点力作用下，弯-扭耦合对梁末端位移及梁末端关于Y轴转角的影响。

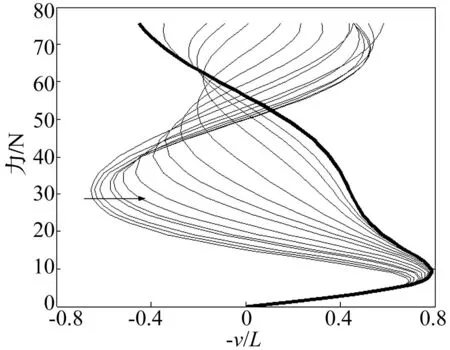
图7　单点力作用下弯扭耦合对Y方向位移的影响Fig.7 The normalized Y displacements impacted by bending and torsion coupling under perpendicular, point, follower force

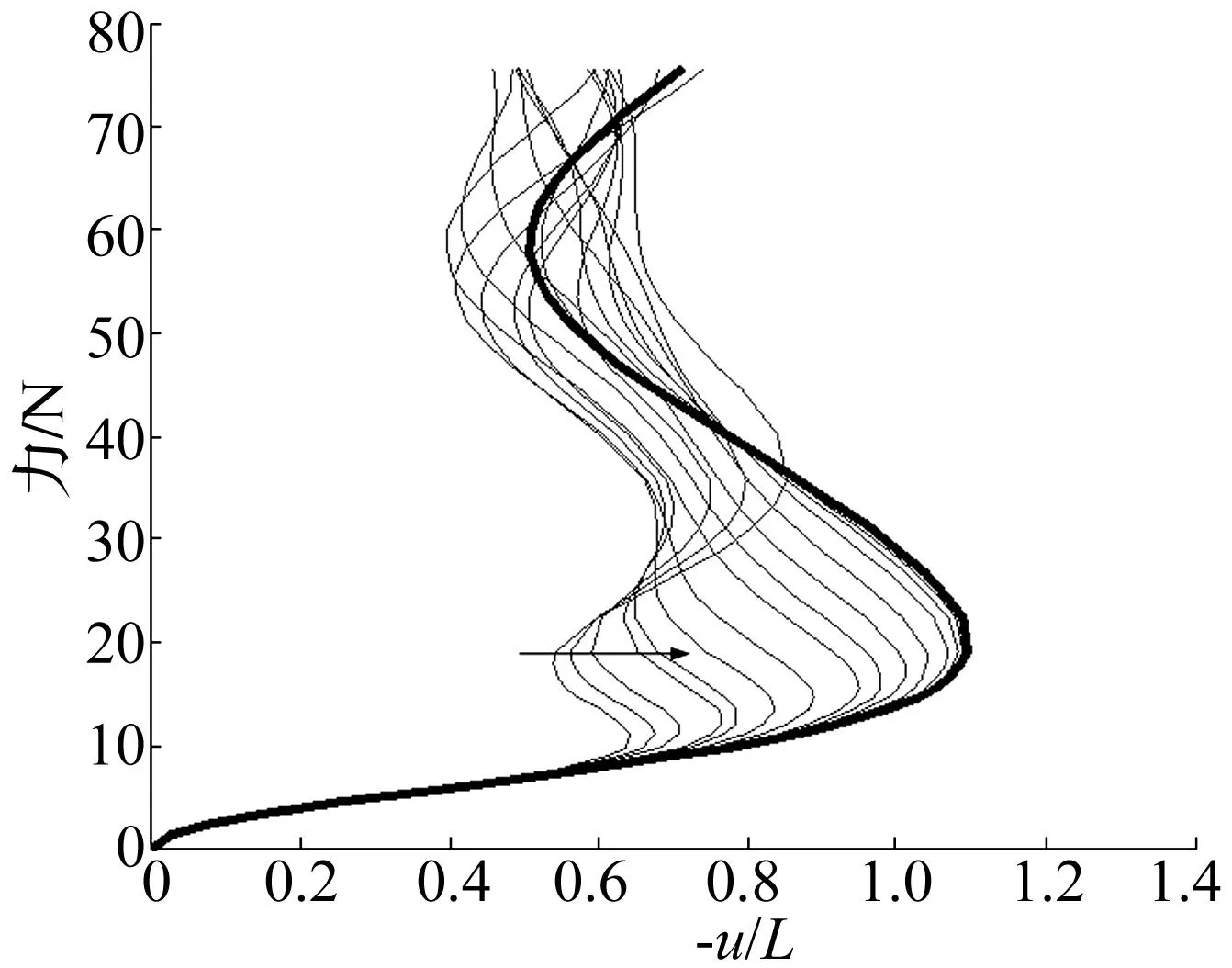
图8单点力作用下弯扭耦合对X方向位移的影响Fig.8 The normalized X displacements impacted by bending and torsion coupling under perpendicular, point, follower force

图9　单点力作用下弯扭耦合对转角的影响Fig.9 The normalized rotations impacted by bending and torsion coupling under perpendicular, point, follower force

图7～图9是弯扭耦合由0.008 kg·m2按图示的箭头分别减小10%，20%，35%，40%，50%，60%，70%，75%，80%，85%，90%，93%，95%和98%得到的弯扭耦合对位移和转角的影响曲线，其中，细实线表示位移和转角随弯扭耦合的变化规律，粗实线表示解耦后位移和转角的变化趋势。由这三幅图可以看出，当载荷约小于10 N时，弯扭耦合对位移和转角的影响较小，当载荷约大于30 N时，弯扭耦合对位移和转角的影响较复杂，当载荷在10～30 N之间时，弯扭耦合的影响开始呈现一定的规律：当弯扭耦合的变化量在0～50%之间时，随着弯扭耦合的变化，梁末端位移及转角的变化趋势与弯扭耦合为0.008 kg·m2(初始时)时的变化趋势相同，当弯扭耦合的变化量大于50%时，位移和转角按另一种变化趋势有规律的变化，但与解耦后相近，当完全解耦后，梁末端的位移及转角的变化趋势与各项同性材料一致，且载荷在10～20 N之间变化时，位移和转角随耦合项成比例的变化。

5结论

(1) 对单层铺层的各向异性材料梁来说，由于其刚度矩阵的耦合项忽略不计，此时的本构方程形式类似于各项同性材料，最终求得的变形构型、梁末端的位移及转角的变化趋势与各项同性材料的一致。

(2) 对刚度矩阵的耦合项不可忽略的各向异性材料来说，刚度矩阵没有解耦之前，耦合项对梁末端位移和转角的影响与载荷有关，载荷较小时耦合项的影响也小，几乎成比例变化，载荷较大时影响复杂，当载荷在10～30 N之间变化时，弯扭耦合以50%的变化量为分界点，分别呈现不同的变化规律，当完全解耦后，位移和转角的变化趋势与各项同性材料一致。

参 考 文 献

[ 1 ] Christensen E R, Lee S W. Nonlinear finite element modeling of the dynamics of unrestrained flexible structures[J]. Computers and Structures, 1986, 23(4): 819-829.

[ 2 ] Belytschko T, Hsieh B. Nonlinear transient finite element analysis with convected coordinates[J]. International Journal for Numerical Methods in Engineering,1973,26(2):255-271.

[ 3 ] Boutaghou Z E, Erdman A G, Stolarski H K. Dynamics of flexible beams and plates in large overall motion[J]. ASME Journal of Applied Mechanics, 1992, 59(4):991-999.

[ 4 ] Hodges D. Geometrically exact, intrinsic theory for dynamics of curved and twisted anisotropic beams[J]. AIAA Journal, 2003, 41 (6): 1131-1137.

[ 5 ] Gatti-Bono C, Perkins N. Physical and numerical modeling of the dynamic behavior of a fly line[J]. Journal of Sound and Vibration, 2002, 255 (3): 555-577.

[ 6 ] 冯志华. 大范围运动柔性梁非线性动力学[D]. 南京：南京航空航天大学, 2002.

[ 7 ] 齐朝晖. 大变形梁的动力学公式及本构关系[J]. 吉林工业大学学报, 1994, 24(73): 24-29.

QI Zhao-hui.Kinetic equations and constitutive relations of large deformation beam[J]. Journal of Jilin University of Technology, 1994, 24(73): 24-29.

[ 8 ] Roberts S, Shipman J. Two-point boundary value problems: shooting methods[M].New York:Elsevier,1972.

[ 9 ] Shvartsman B. Direct method for analysis of flexible beam under a follower load[J]. Proceedings of Computational Mechanics for the Next Millennium, 1999:155-160.

[10] Shvartsman B. Large deflections of a cantilever beam subjected to a follower force[J]. Journal of Sound and Vibration, 2007, 304 (3): 969-973.

[11] Shvartsman B. Direct method for analysis of flexible cantilever beam subjected to two follower forces[J]. International Journal of Non-Linear Mechanics,2009,44(2):249-252.

[12] Karlson K N, Leamy M J. Three-dimensional equilibria of nonlinear pre-curved beams using an intrinsic formulation and shooting[J]. International Journal of Solids and Structures, 2013, 50: 3491-3504.

[13] Hodges D H. Nonlinear composite beam theory[M]. Reston, VA:AIAA, 2006.

[14] Yu W, Hodges D H, Volovoi V V, et al. On timoshenko-like modeling of initially curved and twisted composite beams[J]. International Journal of Solids and Structures,2002,39(19):5101-5121.

[15] Yu W, Hodges D H. Generalized timoshenko theory of the variational asymptotic beam sectional analysis[J]. Journal of the American Helicopter Society, 2005, 50 (1): 46-55.

[16] Yu Wen-bin, Hodges D H, Volovoi V V, et al. On Timoshenko-like modeling of initially curved and twisted composite beams[J]. International Journal of Solids and Structures, 2002, 39: 5101-5121.

[17] Hodges D H. A mixed variational formulation based on exact intrinsic equations for dynamics of moving beams[J]. International Journal of Solids and Structures,1990,26(11):1253-1273.

[18] Leamy M. Intrinsic finite element modeling of nonlinear dynamic response in helical springs[J]. Journal of Computational and Nonlinear Dynamics,2012,7(3):031007.

[19] Cesnik C E S, Hodges D H. VABS: a new concept for composite rotor blade cross-sectional modeling[J]. Journal of the American Helicopter Society, 1997, 42(1): 27-38.

[20] Kovvali R, Hodges D H. Verification of variational asymptotic sectional analysis for initially curved and twisted beams [J]. Journal of Aircraft, 2012, 49(3): 861-869.

[21] Popescu B, Hodges D H. On asymptotically correct Timoshenko-like anisotropic beam theory [J]. International Journal of Solids and Structures, 2000, 37: 535-558.

Geometric nonlinear static equilibria of composite beams using intrinsic formulation

LIYuan-yuan,HEHuan,CHENGuo-ping,LIUPang-lun(The State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:Based on intrinsic beam theory, this paper solved the large deformation buckling problem of geometric nonlinear composite beams.Using the asymptotic variational method, we can get the stiffness matrix of the composite beam in light of material properties.Then, the static behavior of composite beams could be obtained through the balance equation and constitutive equation.The results show that if the composite beam has a single layer, the coupling terms of the stiffness matrix can be ignored and the trends of the deformation configuration, normalized displacements and rotations of the beam end are the same as the isotropic material beams.However, for a general composite beam, the coupling terms of its stiffness matrix cannot be ignored, and the impact of coupling term on displacement and rotation change regularly according to load.When the load is less than 10lb.if the amount of the coupling term change is less than 50%, the displacement and rotation are the same as the initial trends; however, if the change is greater than 50%, they will undergo great changes.

Key words:intrinsic beam theory; composite beam; variational asymptotic method; geometric nonlinearity; large deformation; buckling

中图分类号:V214.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.010

通信作者陈国平 男，博士，教授，1956年7月生

收稿日期：2014-12-03修改稿收到日期：2015-04-20

基金项目：国家自然科学基金资助项目(11472132)；中央高校基本科研业务费资助项目(NS2014002)；江苏高校优势学科建设工程资助项目

第一作者 李园园 女，博士生，1986年3月生