多跨的三种梁的横向自由振动模型

刘向尧， 聂　宏， 魏小辉(南京航空航天大学 机械结构力学及控制国家重点实验室，南京　210016)



多跨的三种梁的横向自由振动模型

刘向尧， 聂宏， 魏小辉(南京航空航天大学 机械结构力学及控制国家重点实验室，南京210016)

摘要：运用了参数变易法对Timoshenko、Rayleigh和Shear梁的横向自由振动模型进行了推导，分析了铰支座、集中质量、转动惯性、拉压弹簧和扭转弹簧的复杂边界条件的情形，进而给出了带有多个复杂边界条件的三种梁的自由振动模型。在其简化的Euler梁下对三个有一定工程实践意义的模型进行了推导，分别是双跨梁、双跨梁带有任意个集中质量和单跨梁带有任意个拉压弹簧的自由振动模型，三个模型的频率方程的结果与已有文献的结果相比具有很好的一致性。并运用Nastran将双跨梁进行了算例分析，该方法提出的公式计算的一阶频率与有限元方法得出的一阶频率之差小于5%，表明提出的模型是合理可用的。

关键词：自由振动； Timoshenko梁；Rayleigh梁；Shear梁；多跨梁

经典的飞机起落架的着陆动力学的相关分析中，将机身视为刚体，用二质量模型进行分析。朱齐丹[1]将此模型应用到舰载机弹射起飞和拦阻动力学的分析中，取得了良好的效果。

现代的大型民用客机由于其机翼尺寸大，新材料的使用使得机翼结构的刚度下降，将机翼甚至整个机体看成弹性体是近年来起落架着陆动力学研究的热点之一。

McPherson等[2-3]将飞机机翼看成自由-自由的Euler梁模型，分析了机翼弹性对安装在机翼的起落架的着陆性能的影响。其应用的对象是上单翼飞机，中单翼飞机如何处理尚未见文献报道；中单翼飞机由于机翼不是整体贯通的，机翼与机身通过加强隔框进行连接，可将连接方式视为铰接。这样可以将单跨的自由-自由的Euler梁模型推广到一般化的多跨梁。

在梁的边界条件方面，现有的分析模型都没有考虑翼吊式发动机的因素，而发动机可以看成带有转动惯性的集中质量。从更一般的角度看，在兵器工业领域，陆毓琪等[4-5]将火炮的身管看成含有集中质量和弹性支撑的弹性梁，给出了单跨梁上的Euler振动模型。王栋等[6]研究了梁附带集中质量的固有频率及其灵敏度计算问题。

在多跨梁研究方面，Гантмахер等[7-8]研究了带有集中质量的多跨Euler梁的定性性质，但是没有给出频率方程，工程技术人员难以直接应用。Ariaei等[9]研究了移动的质量块对多跨的Timoshenko梁动力响应的影响。

本文建立了三种常见的工程梁的自由振动模型，考虑了一些工程上常见的边界条件。应用参数变易法对模型进行分析，推导了自由振动的频率方程。通过简化模型的频率方程与已有文献进行对比，发现两者一致，先前的相关论文结果是本文的特例。该结果可以广泛地应用到各个工程领域，方便工程技术人员使用。

1多跨的三种工程梁的横向自由振动

一般的梁单元，是基于材料力学中的平面变形假定，在这个假定中认为弯曲变形是主要的变形，剪切变形是次要的变形，叫做Euler梁模型。在Euler梁的基础上，只考虑梁绕中性轴的转动惯量一方面因素的为Rayleigh梁模型；只考虑梁剪切变形一方面因素的为Shear梁模型；考虑上述两方面因素的为Timoshenko梁模型[10]。

1.1模型中的基本假设

1) 轴向尺寸明显大于其它两个方向的尺寸；

2) 梁的材料是线弹性；

3) 不考虑泊松效应。

1.2三种工程梁的固有振动

(1)

式中，ρ为单位长度上梁的密度；A为梁的横截面积；w为挠度；β为截面形状系数；G为剪切弹性模量。E为梁的弹性模量；I为梁对截面惯性主轴的转动惯量。

当不考虑剪切变形时，式(1)变为了Rayleigh梁的微分方程

(2)

当不考虑绕中性轴的转动惯量时，式(1)变为了Shear梁的微分方程

(3)

三种梁均具有如下形式的横向固有振动

w(x,t)=W(x)q(t)

(4)

式中，W(x)为梁的振形函数；q(t)为描述运动规律的时间函数。

三种梁的振型函数的通解均为

W(x)=a1chλ1x+a2shλ1x+a3cosλ2x+a4sinλ2x(5)

将式(4)代入式(1)～式(3)中可得对应梁的振形函数。

Timoshenko梁的频率方程为

(6)

其中

α4=ρAω2/EI

(7)

τ=ρω2/E

(8)

σ=ρω2/βG

(9)

式中,ω为Timoshenko梁的固有频率。

Rayleigh梁的频率方程为

(10)

式中,ω为Rayleigh梁的固有频率。

Shear梁的频率方程为

(11)

式中,ω为Shear梁的固有频率。

1.3边界条件

梁的边界条件主要分为两类：简单边界条件和复杂边界条件。简单边界条件指的是梁的约束条件，比如固支，简支等；复杂边界条件指的是安装在梁上的一些力学元件或者其组合，比如集中质量，集中质量和拉压弹簧的组合等。

测定项目包括植物的生长生理指标(生物量、株高、根长、根系活力)和超氧化物歧化酶指标。植物生物量的测定采用电子天平；株高、根长的测定采用卷尺；根系活力的测定采用紫外分光光度计[7]；SOD的测定采用氮蓝四唑(NBT)法[8]。

1) 简单边界条件

一方面讨论在梁两端进行约束的情况，其基本的边界条件可以分为固支、简支、滑支和自由等四种，分别如下：

固支：挠度和转角为0

W=0,W′=0

(12)

简支：挠度和弯矩为0

W=0,W″=0

(13)

滑支：剪力和转角为0

W‴=0,W′=0

(14)

自由：剪力和弯矩为0

W‴=0,W″=0

(15)

在两端进行组合可以得到4×4=16种情况。

另一方面讨论在梁中段有铰支座的情况，其将单跨梁变为了多跨梁。

设梁在γ处有一个铰支座，则铰支座将梁分成了两段，在γ处的挠度为0，转角和弯矩分段连续

(16)

式中,下标1和2分别为梁被简支座分成的两段。

2) 复杂边界条件

关注力学元件，比如集中质量、转动惯性、拉压弹簧和扭转弹簧。

集中质量：设梁在a处有一个集中质量，则集中质量将梁分成了两段，在a处的剪力为集中质量的惯性力

(17)

式中，m为集中质量的质量，Q为剪力。

分离变量，可得

-mω2W(a)=EIW‴(a)

(18)

在a处的挠度，转角和弯矩分段连续

(19)

转动惯性：设梁在e处有一个转动惯性项，则转动惯性项将梁分成了两段，在e处的弯矩由转动惯性项提供

(20)

式中，J为转动惯性项的转动惯量，M表示弯矩。

分离变量，可得

Jω2W′(e)=EIW″(e)

(21)

在e处的挠度，转角和剪力分段连续

(22)

拉压弹簧：设梁在c处有一个拉压弹簧，则拉压弹簧将梁分成了两段，在c处的剪力为拉压弹簧的弹性力

(23)

式中，kt为拉压弹簧的拉压刚度。

分离变量，可得

ktω2W(c)=EIW‴(c)

(24)

在c处的挠度，转角和弯矩分段连续

(25)

扭转弹簧：设梁在d处有一个扭转弹簧，则扭转弹簧将梁分成了两段，在d处的弯矩为扭转弹簧的扭矩

(26)

式中，kθ为扭转弹簧的扭转刚度。

分离变量，可得

-kθW′(d)=EIW″(d)

(27)

在d处的挠度，转角和弯矩分段连续

(28)

1.4带有多个复杂边界条件的多跨梁的自由振动模型

设梁的长度为1，用下标0表示梁的起点，1表示梁的终点；中间的铰支座有k个，每个铰支座的坐标为αi(i=1，2，…，k)；集中质量有n个，每个坐标为bi(i=1，2，…，n)，质量为mi(i=1，2，…，n)，转动惯量为Ji(i=1，2，…，n)；拉压弹簧有f个，每个坐标为ci(i=1，2，…，f)，拉压刚度为ki(i=1，2，…，f)；扭转弹簧有h个，每个坐标为di(i=1，2，…，h)，扭转刚度为kθi(i=1，2，…，h)。

1) 边界条件

中段的铰支座：设中间的第i个铰支座前有nu(0≤nu≤n)个集中质量，fu(0≤fu≤f)个拉压弹簧，hu(0≤hu≤h)个扭转弹簧。

令

u=nu+fu+hu

(29)

则

(30)

(31)

集中质量：设中间的第i个集中质量前有kv(0≤kv≤k)个铰支座，fv(0≤fv≤f)个拉压弹簧，hv(0≤hv≤h)个扭转弹簧。

令

v=kv+fv+hv

(32)

则

(33)

(34)

拉压弹簧：设中间的第i个拉压弹簧前有kx(0≤kx≤k)个铰支座，nx(0≤nx≤n)个集中质量，hx(0≤hx≤h)个扭转弹簧。

令

x=kx+fx+hx

(35)

则

(36)

kiω2W(ci)=EIW‴(ci)

(37)

扭转弹簧：设中间的第i个扭转弹簧前有kz(0≤kz≤k)个铰支座，nz(0≤nz≤n)个集中质量，fz(0≤fz≤f)个拉压弹簧。

令

z=kz+fz+hz

(38)

则

(39)

-kθiW′(di)=EIW″(di)

(40)

其它的复杂边界条件的组合按照上面的思路可以类似得出。

2) 频率方程

频率方程由两端的边界条件确定，将式(12)～式(15)进行组合可以得到4×4=16种情况。

令

s=k+n+f+h

(41)

根据线性系统的叠加性，可以将带有多个复杂边界条件的多跨梁看成由铰支座、集中质量、拉压弹簧和扭转弹簧分开的s+1段梁，即

Wk(x)=ak1chλ1x+ak2shλ1x+

ak3cosλ2x+ak4sinλ2x

(42)

式中，k的取值从1到s+1。

可得4s+4阶的方程组，根据该方程组有非零解可得出频率方程。

2特例

已有论文侧重在Euler梁上进行讨论，根据上文的推导将三种工程梁模型简化到相应的Euler梁模型，通过与已有文献的对比，说明本文建立的模型是合理可用的。特例中的模型是通过Euler梁进行推导得出的，通过本文方法对三种工程梁进行推导也可得出相应结果。

2.1双跨梁情形

令k=1，n=f=h=0，可将模型转换成双跨梁的情形，即梁中间只有一个铰支座，位置是α，将长度为1的Euler梁分成了两段的情形。

特别地，考虑悬臂梁上带有铰支座的情形，其它情形类似可得。其可用于中单翼飞机机体弹性的分析上。根据对称性取一半机体，机翼与机身的连接方式视为铰接。

1) 固支-自由的边界条件

(43)

2) 铰支座的边界条件

(44)

(45)

3) 频率方程

由铰支座分成的每段梁都符合公式

(46)

将式(43)～式(45)代入式(46)中，可得个6阶的方程组，根据该方程组有非零解可得出频率方程

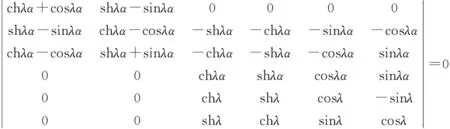
(47)

将上式运用Laplace定理展开，可得频率方程为

(1+ch(1-α)λ·cos(1-α)λ)[shλα·cosλα-

chλα·sinλα]=[sh(1-α)λ·cos(1-α)λ-

ch(1-α)λ·sin(1-α)λ)[1-chλα·cosλα]

(48)

4) 模型验证

将α→1，式(48)变成

tanλ=tanhλ

(49)

式(48)为一端固支，一端铰支的频率方程[10]。

将α→0，式(48)变成

(50)

当α→0时，式(50)是个0/0型的不等式，由三角函数的性质可知，式(50)的右边的分子是比分母更高阶的无穷小量，则

1+chλ·cosλ=0

(51)

式(50)为悬臂梁的频率方程[10]。

5) 算例分析

有限元法是一种工程上常用的数值计算方法。在工程应用领域，常常需要求解各类微分方程，而许多微分方程的解析解有时很难得到，使用有限元法将微分方程离散化后，可以编制程序，使用计算机辅助求解。MSC.Nastran是一款具有可靠性的结构有限元分析软件, 在航空航天领域有广泛的应用。

将Nastran中的数值仿真计算结果与理论推演结果进行对比，证明结果的正确性。

令式(48)中的α=0.5，则铰支座的位置位于梁的中点。

梁的材料为某型合金钢，弹性模量为206 GPa,泊松比为0.3，密度为7 850 kg/m3。梁的截面为实心的矩形截面，长宽均为0.1 m，梁的长度为1 m。

步骤1计算理论解

计算式(48)时，可以先将等式左右的曲线通过MATLAB绘出，明确交点的大致范围，进而可以通过给定个小的允许误差，比如0.01，通过在上面确定的范围进行穷举，逼近理论解。

通过上述方法计算，α=0.5时，λ1=π。代入Euler梁的频率方程可得一阶频率为

f1=233 Hz

步骤2计算数值解

在Patran中进行几何建模，以0.05 m为步长布置网格点，画网格，起始端三个平动和转动自由度全部约束，中点约束三个平动的自由度，赋予材料和梁属性，进行模态分析，读取结果文件，可得一阶频率为

步骤3计算误差

经计算，两者的误差为3%，小于5%。

2.2双跨梁带有任意个集中质量情形

令k=1，f=h=0，可将模型转换成双跨梁带有任意集中质量的情形，即梁中间只有一个铰支座，位置是α，集中质量有n个，每个坐标为bi(i=1，2，…，n)，质量为mi(i=1，2，…，n)，转动惯量为Ji(i=1，2，…，n)，将长度为1的Euler梁分成了n+2段的情形。

特别地，考虑悬臂梁上带有铰支座，铰支座的外侧有任意个集中质量的情形，即bi>α(i=1，2，…，n)，其它情形类似可得。其可用于中单翼飞机机体弹性的分析上。根据对称性取一半机体，机翼与机身的连接方式视为铰接。发动机和挂弹可以视为集中质量。

1) 固支-自由的边界条件

(52)

2) 铰支座的边界条件

同式(44)～式(45)。

3) 集中质量的边界条件

(53)

(54)

4) 频率方程

由铰支座和集中质量分成的n+2段梁都符合式(61)

Wk(x)=ak1cosλx+ak2sinλx+ak3chλx+ak4shλx,

(k=1,…，i，…，n+2)

(55)

将式(52)～式(54)代入式(55)中，可得个4n+6阶的方程组，根据该方程组有非零解可得出频率方程。

5) 模型验证

令n=1，可用于分析翼吊式发动机对机体弹性的影响，则按照先前的方法递推，可得其频率方程为

8+8chλ·cosλ+8pλ(cosλ·shλ-chλ·sinλ)+

(56)

其中

(57)

将表示转动惯量的q=0，可得

1+chλ·cosλ+pλ(cosλ·shλ-

chλ·sinλ)=0

(58)

这与文献[11]给出的结论相同。

2.3单跨梁带有任意个拉压弹簧和集中质量的情形

令k=h=0，可将模型转换成带有单跨梁带有任意个拉压弹簧和集中质量的情形，即梁中间有n个集中质量，位置是bi(i=1，2，…，n)，质量为mi(i=1，2，…，n)，转动惯量为Ji(i=1，2，…，n)；并且梁中间有f个拉压弹簧，每个坐标为ci(i=1，2，…，f)，刚度为ki(i=1，2，…，f)。

特别地，当集中质量和拉压弹簧具有相同的数量，且成对的出现在在同一个位置时，即bi=ci(i=1，2，…，n)，n=f时，可以用此模型分析火炮的身管的弹性问题。

1) 两端的边界条件

由式(12)～式(15)在两端进行组合可以得到4×4=16种情况。

2) 拉压弹簧和集中质量组合的边界条件

(59)

(60)

4) 频率方程

由拉压弹簧和集中质量分成的n+1段梁都符合公式

Wk(x)=ak1cosλx+ak2sinλx+ak3chλx+ak4shλx,

(k=1,…，i，…，n+1)

(61)

将边界条件代入式(61)中，可得个4n+4阶的方程组，根据该方程组有非零解可得出频率方程。

5) 模型验证

将转动惯性项Ji=0，即可得文献[4]的结论。

3结论

运用参数变易法将工程上常用的单跨梁的自由振动模型推广到了多跨梁；将Euler梁推广到了Rayleigh、Shear和Timoshenko梁；将个别的复杂边界条件推广到了一般复杂边界条件及其组合，从而使提出的模型具有更普遍的意义和更广泛的工程实用性。相关文献给出的研究结果可视为本文模型的一种特例。

参 考 文 献

[ 1 ] 朱齐丹，李新飞，喻勇涛.考虑载荷突卸的舰载机弹射起飞动力学分析[J].哈尔滨工程大学学报, 2012, 33(9):1150-1157.

ZHU Qi-dan，LI Xin-fei，YU Yong-tao.Analysis of dynamic characteristics of catapult launch for a carrier-based aircraft with sudden load discharge[J].Journal of Harbin Engineering University, 2012, 33(9):1150-1157.

[ 2 ] McPherson A E，Evans J J,Levy S.Influence of wing flexibility on force-time relation in shock strut following vertical landing impact[R].Washington：NACA，NACA-TN-1995,1949.

[ 3 ] 史友进，张曾錩.大柔性飞机着陆响应弹性机体模型[J].东南大学学报:自然科学版,2005,35(4):549-552.

SHI You-jin, ZHANG Zeng-chang.Elastic model for flexible airplane landing impact analysis[J].Journal of Southeast University:Natural Science Edition, 2005, 35(4): 549-552.

[ 4 ] 陆毓琪,王晓锋,张延教,等.具有任意多个弹性与刚性支承及集中质量的梁振动问题[J].弹道学报,1997,9(4):23-28.

LU Yu-qi, WANG Xiao-feng, ZHANG Yan-jiao,et al.Natural vibration of variable cross section continuous beam with arbitrary lumped mass,elastical and rigid supports[J].Journal of Ballistics, 1997,9(4):23-28.

[ 5 ] 芮筱亭，秦英孝，赵海林,等.有任意个集中质量的转管炮的固有振动[J].兵工学报,1994(2):1-5.

RUI Xiao-ting，QIN Ying-xiao，ZHAO Hai-lin，et al.Natural vibration of spin tube gun with multi-lumped masses[J].Acta Armamentarii,1994(2):1-5.

[ 6 ] 王栋, 马建军.用高阶梁单元计算结构附带集中质量的灵敏度[J].振动与冲击, 2013,32(15):111-115.

WANG Dong, MA Jian-jun.Sensitivity calculation of beam-mass structure using higher-order beam element[J].Journal of Vibration and Shock, 2013,32(15):111-115.

[ 7 ] Гантмахер Ф Р, Крейн М Г.Осцилляционные матрицы и ядра и малые колебания механических систем[M].Москва: Государственное Издательство Технико Теоретической Литературы, 1950:82-208.

[ 8 ] 王其申,章礼华,王大钧.外伸梁离散系统模态的若干定性性质[J].力学学报,2012,44(6):1071-1074.

WANG Qi-shen, ZHANG Li-hua,WANG Da-jun.Some qualitative prosperities of modes of discrete system of beam with overhang[J].Chinese Journal of Theoretical and Applied Mechanics, 2012,44(6):1071-1074.

[ 9 ] Ariaei A, Ziaei-Rad S, Malekzadeh M.Dynamic response of a multi-span Timoshenko beam with internal and external exible constraints subject to a moving mass[J].Archive of Applied Mechanics, 2013, 83(9):1257-1272.

[10] 刘习军，贾启芳.工程振动理论与测试技术[M].北京:高等教育出版社,2004:242-243.

[11] Wang D, Jiang J S, Zhang W H. Frequency optimization with respect to lumped mass position[J]. AIAA Journal,2003,41(9):1780-1787.

The transverse free-vibration model of three multi-span beams

LIUXiang-yao,NIEHong,WEIXiao-hui(State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:The transverse free-vibration equations of Timoshenko, Rayleigh and Shear beam were studied by variation-parameter method.The hinge support, lumped mass, rotational inertia, compression-tension spring and torsional spring were analyzed.Based on these, the free-vibration model of three beams was derived.The analogous Euler beam in its simplified model was proposed to infer the three models with the engineering meanings: the free-vibration model for a two-span beam, a two-span beam with arbitrary lumped masses and a one-span beam with an arbitrary spring-mass system.Comparison between the frequency equations, which were derived by the three models and previous articles, presented good accordance.A two-span-beam example was given by Nastran to compute the first-order frequency.By comparing the result by Nastran with the result from the formula proposed, the error is within 5%, which illustrates that the proposed model is fair and useful.

Key words:free vibration; Timoshenko beam; Rayleigh beam；Shear beam；multi-span beam

中图分类号:V226

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.004

通信作者聂宏 男，教授, 博士生导师，1960年生

收稿日期：2015-01-22修改稿收到日期：2015-05-05

基金项目：国家自然科学基金(51105197;51075203); 江苏高校优势学科建设工程资助项目

第一作者 刘向尧 男，博士生，1984年生

E-mail:hnie@nuaa.edu.cn