桩墙组合基础稳定性求解及影响因素分析
2016-05-19李瑜魏焕卫孔军张伟杨庆义
李瑜,魏焕卫*,孔军,张伟,杨庆义
(1.山东建筑大学 土木工程学院,山东 济南 250014;2.山东电力工程咨询院有限公司,山东 济南250013)
桩墙组合基础稳定性求解及影响因素分析
李瑜1,魏焕卫1*,孔军1,张伟2,杨庆义2
(1.山东建筑大学 土木工程学院,山东 济南 250014;2.山东电力工程咨询院有限公司,山东 济南250013)
桩墙组合基础是一种主要承受水平荷载的新型基础,对其进行稳定性求解及影响因素分析有利于指导实际工程应用。文章基于墙、桩、土侧向变形共同作用的原理,提出了组合基础稳定性求解方法,针对桩墙组合基础在水平荷载的情况,通过 MATLAB编制的计算程序,分析了水平荷载的大小、墙身的宽度、桩径尺寸、土的性质以及材料弹性模量等因素对组合基础变形和内力的影响。结果表明:组合基础的最大位移出现在基础顶部,最大弯矩出现在墙与桩的刚接部位;墙宽的大小和桩径的大小都与组合基础最大位移成反比,但墙宽增加到6 m或者桩径增加到0.8 m后,组合基础最大位移的减小速率减缓;土抗力增加,组合基础的最大位移减小,m值增加到10 MN/m4后,组合基础的变形趋于定值,土抗力对基础内力影响不大;组合基础材料的弹性模量对基础的位移与弯矩影响不大。
共同作用;桩与地下连续墙组合基础;水平荷载;侧向变形
0 引言
在电厂建筑中,由于锅炉等建筑物生产工艺的特殊性,建筑物基础往往会承受很大的水平承载力;在海洋建筑中,基础也会受到波浪力、水平地震力、船舶撞击力等水平荷载作用。以往的解决方案往往是扩大桩的直径和数量或者采用地下连续墙基础。但是,这样会造成很大的浪费。对于桩墙组合基础,国内外研究的不是很多,大多数研究都是针对单一基础类型[1-3]。孙学先等在国内首次现场模拟了单片墙的水平承载力和侧摩阻力[2];张瑞棋等通过现场试验对陇东黄土地区刚性地下连续墙桥梁基础水平承载力特性进行研究[3];戴国亮等通过对三片单片墙进行模型试验,研究了单室井筒式地下连续墙基础的水平承载特性[4];周香琴对井筒式地下连续墙基础水平承载特性进行了试验研究[5];刘念武等对地下连续墙在软土地基中的变形特性进行分析[6]。上述研究表明地下连续墙具有良好的水平承载特性。魏焕卫等分析了桩在侧向受荷条件下的侧向变形和内力特性[7-8];李国豪依据桩的水平位移现场测试结果,对桩的弯曲变形、弯矩和土体位移作出了理论分析[9];陈正等通过有限元模拟和现场实测结果比较,给出各个参数的合理取值[10];常林越等对地基反力系数法和桩侧土体简化的弹塑性本构关系进行分析[11];王国粹等采用针对双曲线模型现行多种砂土中水平受荷桩的 p—y曲线形式进行拟合归一化[12];蔡忠祥等基于混凝土损伤模型对灌注桩水平承载性状进行分析[13];王卫东等着重分析了墙—桩—箱复合基础共同作用的问题,推导了墙—桩—土位移影响系数[14-15]。上述学者提供了桩基础在水平荷载作用下的分析计算方法。在已有的研究基础上,文章主要以变形控制作为目标,建立起桩墙组合基础稳定性分析方法,同时利用MATLAB编制的有限元计算程序对组合基础的受力特性做出初步分析。
1 桩墙组合基础稳定性求解
文章研究了一种新型基础—桩墙组合基础(如图1所示)。该组合基础上部为地下连续墙,下部为桩,两部分交界处刚接。

图1 桩墙组合基础示意图
1.1 土压力求解公式
根据朗肯土压力理论假设墙背光滑直立、墙后填土面水平。桩墙组合基础主要承受水平荷载为Vk,主动土压力为 Pa,被动土压力为 Pp,墙侧摩阻力为fi(如图2所示)。在实际情况中,墙体内部的土芯也会对组合基础产生影响,为方便计算,这里忽略内部土芯对组合基础的影响。
1.1.1 主动土压力求解公式
受荷一侧主动土压力由式(1)表示为

式中:Ea为主动土压力强度,kN/m;H为墙身高度,m;z0为临界深度,m;σaB为墙底工压力强度,kPa。
整面墙体所承受土压力由式(2)表示为

式中:Pa为墙体承受的土压力,kN;B为墙身宽度,m。

图2 组合基础受力分析图
1.1.2 被动土压力求解公式
远离水平荷载侧被动土压力由式(3)表示为

式中:E0为被动土压力强度,kN/m;σpD、σpC分别为墙顶与墙底土压力强度,kPa。
远离集中荷载侧墙体所承受的土压力由式(4)表示为

式中:Pp为墙体承受的土压力,kN。
1.2 侧墙受土摩擦力求解公式
两面侧墙墙体承受侧摩阻力由式(5)表示为

式中:f为墙侧侧阻值,kN;L为侧面墙身宽度,m;qsia为墙侧阻力特征值,qsia,kPa;由当地静载荷试验结果统计分析算得;li为第i层土的厚度,m。
1.3 抗滑移验算
假设组合基础在水平荷载作用下组合基础两侧均同时达到极限平衡。此时,组合基础的滑动力主要为水平荷载与主动土压力,抗滑力主要由墙侧摩阻力、桩的水平承载力与被动土压力提供。当组合基础所受的滑动力小于其所受的抗滑力时,组合基础处于安全状态,由式(6)表示为
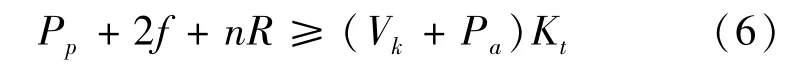
式中:Vk为集中荷载,kN;n为桩的数量;Kt为安全系数;R为桩体水平承载力,kN。
按照JGJ 94—2008《建筑桩基技术规范》[16]桩水平承载力由式(7)、(8)表示。
当桩身配筋率小于0.65%时,


式中:EI为桩身抗弯刚度,kN/m2;υx为桩顶水平位移系数;χ0a为桩顶允许水平位移,m。
1.4 抗倾覆验算
组合基础在水平荷载下的倾覆力矩主要应为水平荷载与主动土压力产生,而抗倾覆力矩主要是由墙侧摩阻力与被动土压力提供。为了满足组合基础的使用要求,应使组合基础的抗倾覆力矩大于倾覆力矩。对桩与墙连接处C点取矩,由式(9)表示为

式中:α为桩的水平变形系数;γm为桩截面模量塑性系数;ft为桩身混凝土抗拉强度设计值,kPa;W0为桩身换算截面受拉边缘的截面模量,m3;vM为桩身最大弯矩系数;ρg为桩身配筋率;ζN为桩顶竖向力影响系数;Nk为在荷载效应标准组合下桩顶竖向力,kN;An为桩身换算截面积,m2。
当桩身配筋率大于0.65%时,
式中:xa、xp为主动土压力与被动土压力的作用位置,xa=H/3,xp=(H/3)·[(2σpD+σpC)/(σpD+σpC)]x,m;fi为第 i层土的侧阻值,kN;li为第 i层土的厚度,m;Ks为安全系数。
1.5 桩墙连接处节点验算
1.5.1 抗剪切验算
在水平荷载作用下,组合基础会发生水平方向的位移,此时,桩墙连接处的节点受到剪切力作用,可能发生剪切破坏。按照 GB 50010—2010《混凝土结构设计规范》[17],在组合基础的节点处需要满足公式(10)为
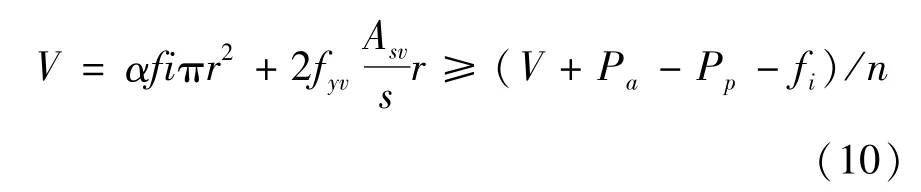
式中:V为桩体受剪承载力设计值,N;ft为混凝土轴心抗拉强度设计值,N/mm2;α为截面受剪承载力系数,此处取 0.7;r为桩体半径,m;Asv为配置在同一截面内箍筋全部截面面积,mm2;s为沿构件长度方向的箍筋间距,mm;fyv为箍筋抗拉强度设计值,N/mm2。
1.5.2 抗弯承载力验算
组合基础受水平荷载时,在桩墙连接处会产生弯矩。所以,需要对此处进行抗弯承载力的验算,根据JGJ 120—2012《建筑基坑支护技术规程》[18]中的规定,节点需要满足式(11)为

式中:M为桩的弯矩设计值,kN·m;fc为混凝土轴心抗压强度设计值,kN/m2;A为桩身截面面积,m2;r为桩身半径,m;α为对应于受压区混凝土截面面积的圆心角与2π的比值;fy为纵向钢筋抗拉强度设计值,kN/m2;As为全部纵向钢筋的截面面积,m2;rs为纵向钢筋重心所在圆周的半径,m;αt为纵向受拉钢筋截面面积与全部纵向钢筋截面面积的比值,当 α >0.625时,取 αt=0。
1.6 有限元分析
根据“共同作用”方法,对土的侧向弹性抗力系数采用“m”法,即假定k(z)=m×z(z为深度)进行有限元分析。如图3所示,把桩墙组合基础划分为 n个单元,则该结构有 n+1个节点。每个单元的长度为相邻两个单元长度之和的一半,其宽度记为 Bi。假设墙、桩、土的接触面上的径向作用力均布在各个单元上,以合力的形式作用在节点上。
因为在桩与墙的单元上,每个节点的自由度为2,其单元刚度矩阵[K]e由式(12)表示。

式中:I为单元惯性矩,m4;E0为墙或桩单元的弹性模量,MPa;L为墙或桩单元长度。

图3 有限元分析图
根据土的侧向弹性抗力系数求得土对组合基础的反力矩阵由式(13)表示为

将[Kt]、{w}的阶数也扩大一倍,令相应于转动分量的元素为零,并记为由桩土侧向变形协调关系得式(15)为

式中:{R}为墙、桩土作用力向量。对单刚[K]e进行对号入座集成单元刚度矩阵[K],得到墙、桩与土共同作用的式(16)为

式中:P为外荷载向量 P=[P00 … 0]Tn+1。
解式(16)得到节点位移向量,单元节点力和单元节点位移的关系如式(17),得到各节点内力。利用非节点处截面位移与内力和节点位移的关系,可进一步计算任意截面处的位移和内力。

式 中:{F}e为 墙 或桩 单元 节 点 力,{F}e=[Q1M1Q2M2];{U}e为墙或桩单元节点位移,{U}e=[w11 w22]T;
2 桩墙组合基础稳定性影响因素分析
影响桩墙组合基础位移与内力的因素主要有水平荷载的大小、墙身的宽度、桩径尺寸、土的性质以及混凝土弹性模量等。进行有限元分析时所需要的参数如下:H为3 m、h为6 m、l为4 m、b为1 m、d为0.8 m、n为4,m为12 MN/m4、E0为30000 MPa和P0为 800 kN。
2.1 水平荷载对组合基础变形与内力的影响
由组合基础的不同水平荷载与侧向变形关系图(如图4所示)可以看出,(1)组合基础的最大位移在基础顶部,之后组合基础的位移沿深度方向呈线性减小,在7 m附近出现零点,随后位移沿反方向增大。(2)随着水平荷载增加,组合基础的位移逐渐增大,但在深度为7 m的区域,出现反向拐点,组合基础围绕该点发生了转动。出现拐点的主要原因是,上部墙体结构刚度足够大,则组合基础整体具有足够大的刚度,基础呈整体倾斜破坏特征。随入土深度的增加,墙体的角位移变化甚小,位移随深度的变化近似为线性变化,所以,组合基础可以抵抗较大的水平力。随着深度的增加,墙侧摩阻力与被动土压力开始发挥作用,位移逐渐减小。
根据不同水平荷载与弯矩关系图(如图 5所示)可得,(1)水平荷载增加,组合基础的弯矩增大;(2)组合基础沿深度方向弯矩首先增大,在桩与墙连接处附近达到弯矩最大值,然后迅速减小直至为零。主要是因为随着深度的增加,主动土压力逐渐增大,虽然被动土压力与墙侧摩阻力也相对增大,但抗力产生的弯矩仍不足以平衡水平荷载与主动土压力产生的弯矩。在组合基础下部弯矩较小的原因是被动土压力与墙侧摩阻力所提供的弯矩足够大。在桩墙连接处弯矩达到最大值,是因为墙身与桩身在受力面积上相差很大,造成了在此处刚度发生突变。所以,桩墙刚接处位置为组合基础的最不利影响位置,在实际工程中应该格外注意刚接处的设计与施工。

图4 不同水平荷载与侧向变形关系图

图5 不同水平荷载与弯矩关系图
2.2 墙身宽度对组合基础变形与内力的影响
在墙身宽度影响下组合基础的侧向变形与弯矩图(如图6所示)中,随着墙身宽度的减小,组合基础的上部的侧向位移逐渐增大,但是组合基础下部的位移变化相对较小。其形成原因是墙身宽度越大,组合基础的刚度越大,组合基础的侧向变形越小。随着入土深度的增加,水平荷载对组合基础的作用效果逐渐消散,桩基础部分所承担的位移与弯矩相对较小。在组合基础中桩基部分起到了很好地嵌固效果。墙身宽度减小,墙身弯矩变化不大,桩与墙连接处和桩身弯矩增大较为明显。因为墙身宽度减小,而桩径不变,使得桩身刚度与墙身刚度之比增加,桩身将分配到更多的弯矩。所以,在桩墙刚接处与桩体上,弯矩有所增加。

图6 墙身宽度影响下组合基础的侧向变形与弯矩图
在组合基础顶部侧向变形与墙宽的关系曲线图(如图7所示)中,当墙身宽度从 2 m增加到 6 m后,组合基础的水平位移减小了4.9 mm,但是墙身宽度从6 m增加到10 m后,组合基础的水平位移仅仅减少了1 mm。由此可以推断,墙身宽度越大,组合基础顶部的侧向变形越小,但是随着墙身宽度的继续增加,基础顶部的侧向变形逐渐趋于定值。这说明,在一定范围内增加墙身宽度,可以有效地控制组合基础的最大位移,超出此范围后,再增加墙身宽度对位移控制效果不明显。所以,在实际工程当中,应该特别注意墙身宽度的选取,使得基础既不能太浪费,又不能让桩承担较大的弯矩。

图7 组合基础顶部侧向变形与墙宽的关系曲线图
2.3 桩径对组合基础变形与内力的影响
桩径影响下组合基础的侧向变形与弯矩图(如图8所示)可得(1)桩径较小时,桩身刚度相对较小,桩身变形出现非线性变化。桩径增大后,组合基础沿深度方向的变形趋于线性;(2)随着桩径增大,组合基础位移减小,但是墙身部分位移变化较大,桩基础部分位移变化较小。进一步验证了在组合基础中,桩起到了良好的嵌固作用。桩径增大,桩与墙连接处、桩身弯矩增大,墙身弯矩变化较小。这是因为,无论墙身尺寸的改变还是桩径的变化,都将影响组合基础整体的刚度分布,进而影响组合基础上弯矩的分配,从而使得桩身承担较大的弯矩。而桩径增大,桩土接触面面积增大,其桩身内力也会随之增大。因此,在实际工程中,桩径的选择也尤为重要。

图8 桩径影响下组合基础的侧向变形与弯矩图
桩径顶部侧向变形与桩径的关系曲线图(如图9所示)显示。桩径从0.2 m增加到0.6 m后,组合基础顶部的侧向位移减小了10.1 mm。而当桩径从0.8 m增大到1 m后,组合基础顶部的位移仅减小了0.62 mm。由此可知,随着桩径增大,组合基础最大位移迅速减小,随后变化速率减缓。所以,适当的增加桩径可以有效地限制组合基础的侧向位移。但当桩径达到一定数值时,再增加桩径,不仅对组合基础位移控制的效果不明显,还会增大桩身弯矩。
2.4 土的性质对组合基础变形与内力的影响
这里考虑土层的地基反力系数的比例系数 m对桩墙组合基础侧向变形与内力的影响。m值越大,相同深度的地基反力系数就越大,土能提供的抗力也就越大,组合基础的侧向变形就越小。在m值影响下组合基础的侧向变形与弯矩图(如图 10所示)中,随着 m值的增加,组合基础的侧向位移减小,符合上述规律,但是组合基础的弯矩几乎不变。这是因为,地基反力系数的比例系数的改变会影响组合基础的响应,但对组合基础弯矩的影响较小[19],因此在常见的土层中,地基反力系数的比例系数对组合基础的弯矩几乎无影响。当土质较差时,更应该注意限制组合基础的侧向位移,而不是增强组合基础本身的强度。

图9 桩径顶部侧向变形与桩径的关系曲线图
组合基础顶部侧向变形与 m值的关系曲线图(如图11所示)中可以发现,m值从4 MN/m4增加到 10 MN/m4后,组合基础顶部的侧向位移减小了7.2 mm,m值从10 MN/m4增加到22 MN/m4后,组合基础顶部的侧向位移仅减小了 2.7 mm。所以可以推断出,随着 m值的不断增加,组合基础顶部的位移迅速减小,当 m值增加到一定数值后,组合基础顶部的位移变化速度变小。因此,在实际工程中,有时单纯的地基加固,并不能很好地控制组合基础的变形,应该考虑增加组合基础的尺寸来限制其位移。

图10 m值影响下组合基础的侧向变形与弯矩图
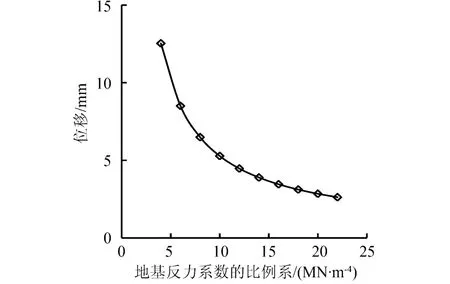
图11 组合基础顶部侧向变形与 m值的关系曲线图
2.5 弹性模量对组合基础变形与内力的影响
由弹性模量影响下组合基础的侧向变形与弯矩图(如图12所示)可以发现,四条曲线几乎是重合的,当组合基础材料的弹性模量逐渐增大时,组合基础的侧向变形和弯矩几乎没有变化。这说明,组合基础材料的弹性模量对其承担水平荷载时的侧向位移与弯矩影响不大。由此可以推断出,对于承担水平荷载的组合基础,在满足组合基础竖向承载力条件下,应尽量选择低等级的混凝土做组合基础的材料。因为采用高强度混凝土,不仅不能提高组合基础的水平抗力,而且混凝土的强度也得不到充分利用,造成一定的浪费。
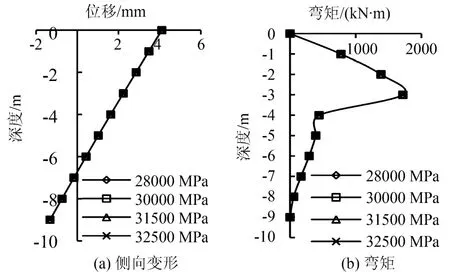
图12 弹性模量影响下组合基础的侧向变形与弯矩图
3 结论
通过上述研究可知:
(1)组合基础的最大位移出现在基础顶部,最大弯矩出现在墙与桩的刚接部位。桩墙连接部位建议桩身嵌入墙内的尺寸不宜小于 50 mm,对于大直径桩嵌入墙内尺寸不宜小于100 mm。桩顶纵向主筋应锚入墙内,其锚入长度不宜小于 35倍纵向主筋直径。
(2)墙宽的大小和桩径的大小都与组合基础最大位移成反比,但是当墙宽增加到6 m或者桩径增加到0.8 m后,基础顶部位移趋于定值。减小墙宽和增加桩径会使桩身分担到更大弯矩。所以,在设计时,应当选取合适的墙宽与桩径,在满足变形要求的情况下尽量减小桩身弯矩。
(3)土抗力越大,组合基础的位移就越小。当m值增加到10 MN/m4后,组合基础的位移减小速率减缓,而土抗力对组合基础弯矩的影响较小。因而,当土质较为复杂时,更加注重对组合基础变形的控制。
(4)组合基础材料的弹性模量对基础的位移与弯矩影响不大。所以,中低强度的混凝土即可满足实际需要。
[1] 地中連続壁基礎協会連壁基礎施工検討委員会.地中連続壁基礎工法ハソドブツク(設計編)[M].東京:日本総合土木研究所,1993.
[2] 孙学先,崔文鉴.Q4黄土地基地下连续墙水平承载模型试验研究明[J].兰州铁道学院学报,1995(03):49-54.
[3] 张瑞棋,黄志军.陇东黄土地区刚性地下连续墙桥梁基础水平承载力特性研究[J].路基工程,2012(3):97-99.
[4] 戴国亮,周香琴,刘云忠,等.井筒式地下连续墙水平承载能力模型试验研究[J].岩土力学,2011,32(S2):185-197.
[5] 周香琴.井筒式地下连续墙基础水平承载特性试验研究[D].南京:东南大学,2011.
[6] 刘念武,龚晓南,楼春晖.软土地基中地下连续墙用作基坑围护的变形特性分析[J].岩石力学与工程学报,2014,33(S1):2707-2712.
[7] 魏焕卫,崔冠科,宋菲.桩的侧向变形和竖向荷载的耦合分析[J].结构工程师,2010,26(2):137-141.
[8] 魏焕卫,李俊,徐德亭.侧向受荷桩基变形和受力规律的研究[J].山东建筑大学学报,2010,25(3):293-296.
[9] 李国豪.关于桩的水平位移,内力和承载力的分析[J].力学季刊,1981(1):1-10.
[10]陈正,梅岭,梅国雄.柔性微型桩水平承载力数值模拟[J].岩土力学,2011,32(7):2219-2224.
[11]常林越,王金昌.双层弹塑性地基水平受荷桩解析计算[J].岩土工程学报,2011,33(3):433-440.
[12]王国粹,杨敏.砂土中水平受荷桩非线性分析[J].岩土力学,2011,32(S2):261-267.
[13]蔡忠祥,刘陕南,高承勇,等.基于混凝土损伤模型的灌注桩水平承载性状分析[J].岩石力学与工程学报,2014,33(S2):4032-4040.
[14]王卫东,李桂花.墙—桩—箱复合基础共同作用研究[J].地下工程与隧道,1995(3):15-19.
[15]王卫东,李桂花.墙—桩—箱复合基础共同作用研究(续)[J].地下工程与隧道,1995(4):12-17.
[16]JGJ 94—2008,建筑桩基技术规范[S].北京:中国建筑工业出版社,2008.
[17]GB 50010—2010,混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.
[18]JGJ 120—2012,建筑基坑支护技术规程[S].北京:中国建筑工业出版社,2012.
[19]黄朝煊.地基土反力系数对水平受荷单桩响应的影响分析[J].中国农村水利水电,2013(9):122-125.
Solution and influeuce factor analysis of piles-diaphragm wall combined foundation under lateral concentrated load
Li Yu,Wei Huanwei,Kong Jun,et al.
(School of Civil Engineering,Shandong Jianzhu University,Jinan 250014,China)
Piles-diaphragm wall combined foundation is a new foundation for horizontal load,and the research on it is helpful to guiding the engineering practice.Based on the principle of wall,pile and soil lateral deformation,this paper puts forward a method for stability analysis of composite foundation.For the piles-diaphragm wall combined foundation in the horizontal load,by MATLAB,it mainly explores the horizontal load size,the width of the wall body,pile diameter size,soil properties and material elastic modulus and other influencing factors on deformation and internal force of combined foundation.Results show:the maximum displacement of the combined foundation is at the top of the foundation,and the maximum bending moment is at the wall and the pile's rigid connection position;the size of the wall width and the diameter of the pile are all inversely proportional to the maximum displacement of the combined foundation,but when the wall width increases to 6m or pile diameter increases to 0.8 m,the maximum displacement of the combined foundation decreases with the decrease of the maximum displacement;with the increase of soil resistance,the maximum displacement of the composite foundation decreases,the m value increases to 10MN/m4,the deformation of the composite foundation tends to the fixed value,and the soil resistance has littleeffect on the internal force of the foundation;elestic modulus of combined foundation have little influence on displacement and bending moment of foundation.
interaction;pile and diaphragm wall combination foundation;horizontal load;lateral deformation
TU 443
A
1673-7644(2016)05-0458-08
2016-08-05
山东电力工程咨询院有限公司横向课题项目(K22014016)
李瑜(1992-),男,在读硕士,主要从事地基基础等方面的研究.E-mail:446174990@qq.com
*:魏焕卫(1974-),男,副教授,博士,主要从事岩土共同作用和变形控制等方面的研究.E-mail:13181718169@163.com
