单个移动集中荷载下简支梁的弹性临界弯矩

褚昊，郭兵，管海龙

（山东建筑大学土木工程学院，山东 济南 250101）

单个移动集中荷载下简支梁的弹性临界弯矩

褚昊，郭兵*，管海龙

（山东建筑大学土木工程学院，山东 济南 250101）

简支梁的临界弯矩计算公式都有其特定的适用范围，其中单个集中荷载下的计算公式只能适用于荷载作用于特殊位置的情况，当荷载作用在其他位置时计算结果偏差较大。文章基于Bleich的总势能公式，假设了可以模拟任意弯扭变形及弯矩图的函数，围绕单个集中荷载作用于任意位置时简支梁的临界弯矩展开研究，通过瑞利—里兹法，分析了单个集中荷载处于简支梁任意位置时临界弯矩的计算公式，并通过函数拟合，提出了公式中相关参数的简化计算方法，同时进行算例分析，验证所给公式的精确性。结果表明：文章所给的临界弯矩计算公式能够计算单个集中荷载作用于简支梁任意位置时的临界弯矩；公式形式与传统公式一致，但公式中参数 C1、C2、C3不再是具体数值，改用计算公式表达，适用范围更广；文章算例中，所给公式的计算结果与传统计算方法所得结果最大偏差仅为5.4%。

简支梁；单个移动荷载；弹性临界弯矩；瑞利—里兹法

0 引言

受弯构件的整体稳定问题一直存在争议，国内外众多学者都曾对简支梁的弯扭屈曲问题进行过研究［1－6］。GB 50017－2003《钢结构设计规范》在计算及弯构件的整体是系数时用到了弹性临界弯矩［7－8］。但其给出的 Mcr计算方法不能涵盖所有的受荷情况。

推导临界弯矩的总势能公式主要有 Bleich公式［9］、童根树公式［10］和 吕 烈 武 公 式［11］。目 前，计 算弹性临界弯矩的方法很多，Kirby提出横向荷载作用于剪心时 Mcr的计算公式［12］，陈绍蕃提出荷载作用于上、下翼缘时Mcr的计算方法［13］，但二者都有其特定的适用范围，而使用等效弯矩系数法，是将非均匀受弯等效成均匀受弯的近似方法；周绪红等［14］和刘占科等［15］提出了荷载作用在任意位置时 Mcr的通用计算公式，但其采用的变形函数相对简单，只能适用于对称荷载，当荷载非对称时，计算结果偏差较大。Clark等提出三参数法，通过 C1、C2、C3三个参数综合考虑各因素对弹性临界弯矩值的影响，计算精度较高。文章将依据Bleich的总势能公式，采用可以模拟任意弯扭变形的位移函数和弯矩表达式，通过瑞利—里兹法和三参数法，推导单个移动集中荷载作用下简支梁的 Mcr计算公式。

1 基本假设

对于单个集中荷载 P作用下的单向受弯简支梁，由 Bleich总势能公式可得构件的总势能，由式（1）表示为

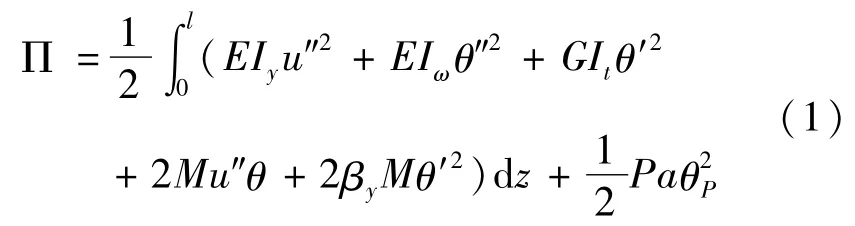
式中：П为总势能，J；l为简支梁的跨度，m；E、G分别为弹性模量和剪切模量，N／mm2；Iy、It分别为绕y轴的惯性矩、自由扭转惯性矩，mm4；Iω为绕y轴的翘曲惯性矩，mm6；βy为截面不对称参数；M为z坐标处的截面弯矩，kN·m；u为 z坐标处的剪心侧向位移，mm；θ为z坐标处的截面扭转角；a为荷载P作用点到剪心S的距离，mm；荷载作用点位于受压区时a取负值，反之取正值；θP为P作用处的截面扭转角；如图1所示。图1中，P代表集中荷载，kN；zP表示荷载作用点距简支梁端的距离，m；S、O分别为截面的剪心和形心；S′、O′分别为构件发生位移后截面的剪心和形心。

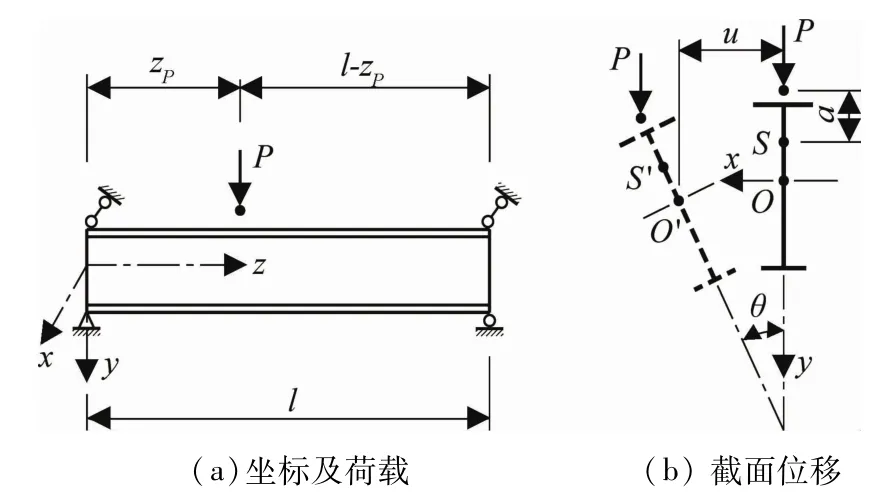
图1 构件坐标、荷载及截面侧向弯扭位移图

1.1 弯扭变形函数

假设构件的侧向位移 u、扭转角θ分别由式（2）～（5）表示为

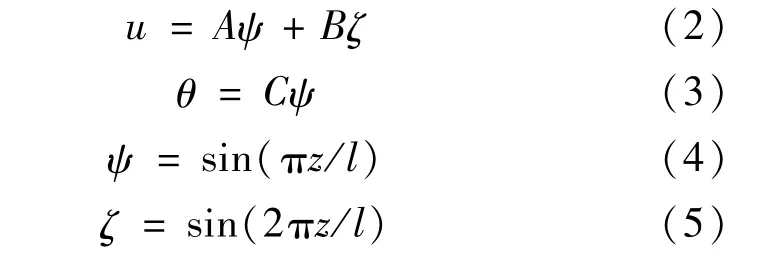
式中：A、B、C分别为独立的广义坐标；ψ、ζ分别为基函数。

则 P作用处的截面扭转角由式（6）表示为

1.2 弯矩表达式

单个集中荷载作用下，简支梁的最大弯矩由式（7）表示为

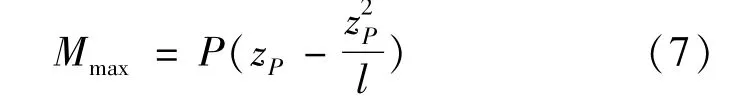
则构件上任意z坐标处的弯矩M分别由式（8）～（9）表示为

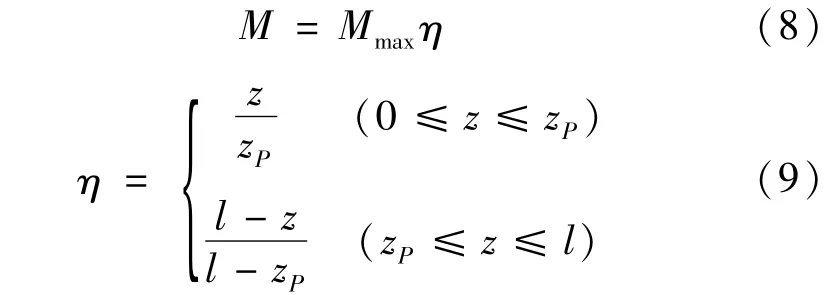
稳定分析时还需建立P与Mmax的式（10）关系，引入等效力臂e，令

将式（7）代入式（10）可得式（11）为

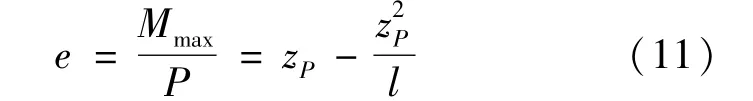
2 简支梁临界弯矩的通用公式

2.1 临界弯矩公式及参数表达式

将式（2）～（11）带入总势能公式（1），并逐项分解由式（12）～（17）表示为

为方便表达，引入参数由式（18）～（25）表示为

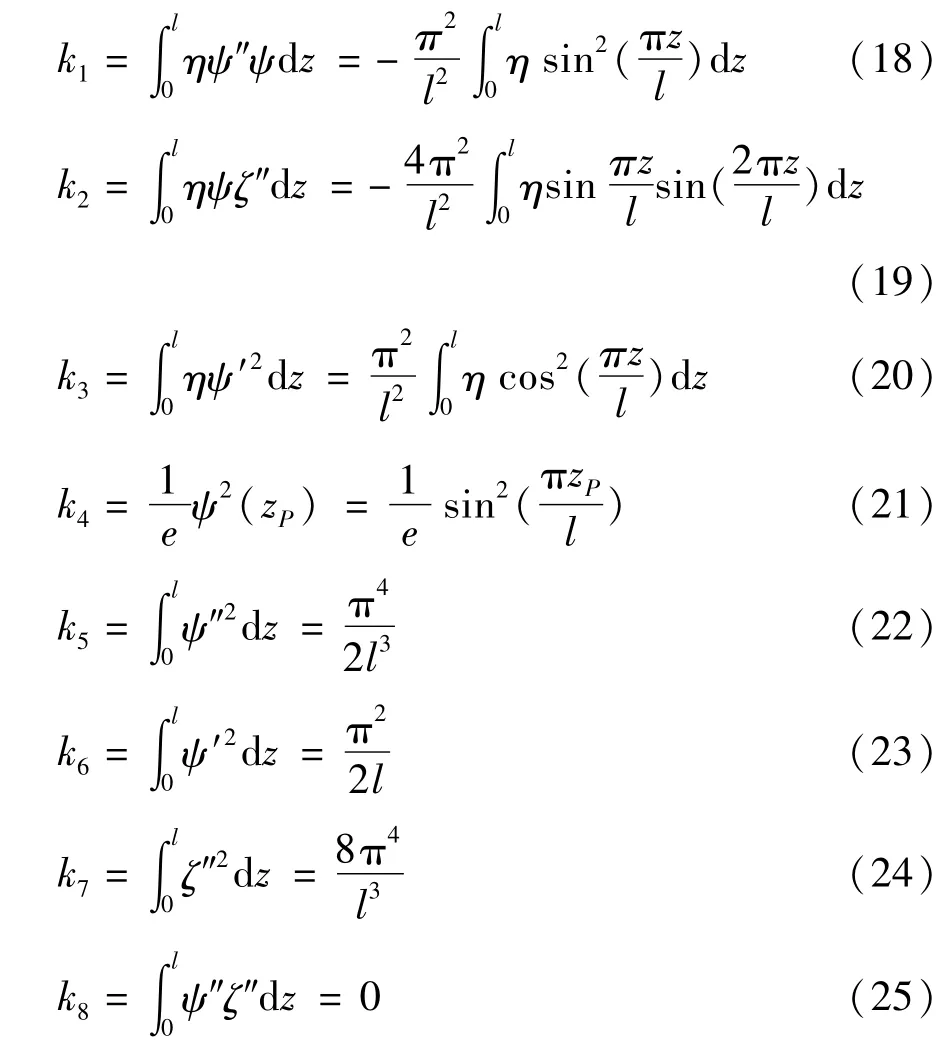
总势能由式（26）表示为

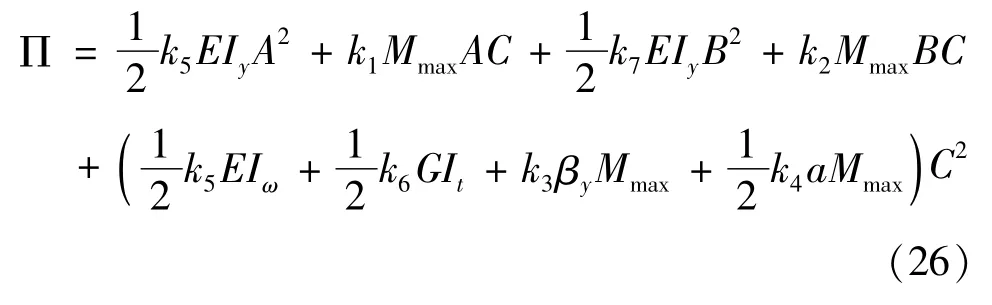
在式（26）中，根据势能驻值原理 ∂Π／∂A＝0、∂Π／∂B＝0、∂Π／∂C＝0可得线性方程组由式（27）～（29）表示为

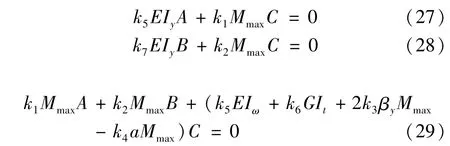
线性方程组恒成立的条件是系数行列式（30）为零，即

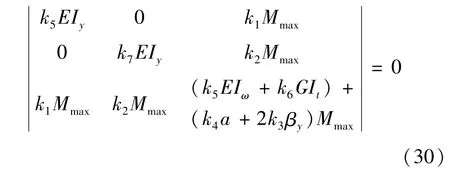
可得特征方程式（31）为

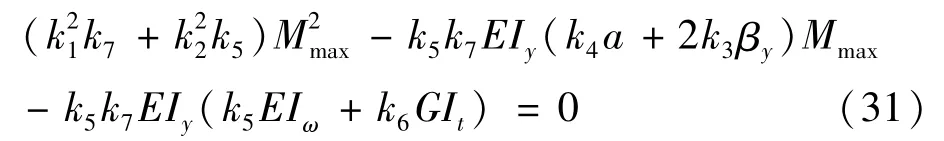
将 k5、k6、k7的值代入上式可解得 Mmax的最小值，也即临界弯矩由式（32）表示为

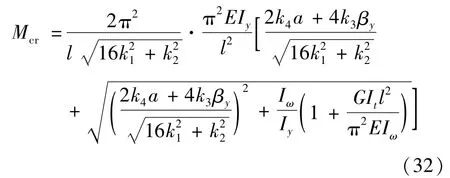
为方便与传统公式相对照，将式（32）写成式（33）为

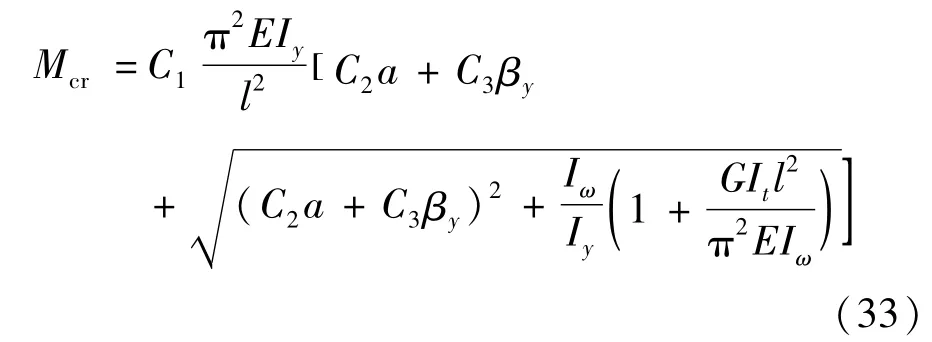
其中，参数 C1、C2、C3的表达式分别由式（34）～（36）表示为

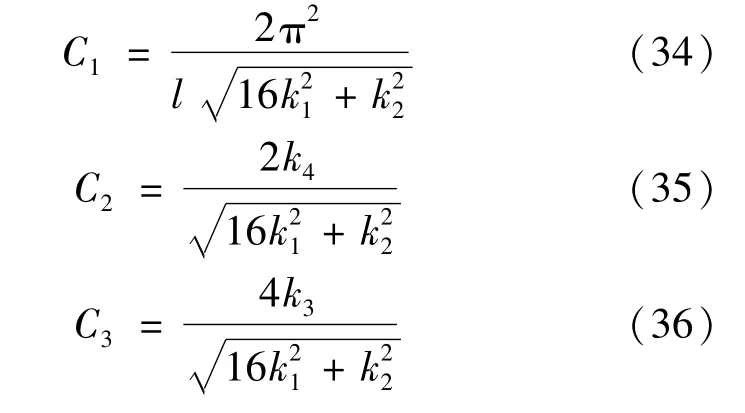
2.2 典型算例验证

当跨中央作用一个集中荷载时，zP＝l／2、Mmax＝Pl／4，此时式（9）简化为式（37）为

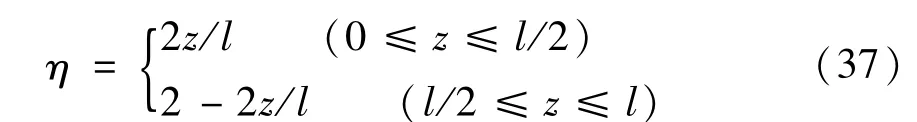
式（11）简化为式（38）为

将上述参数代入式（18）～（21）可得

再将 k1～k4代入式（34）～（36）可得 C1＝1.42、C2＝0.58，C3＝0.42；传统公式所得解［17］为 C1＝1.37，C2＝0.55和C3＝0.41，三个参数中的最大偏差为5.4%，由此计算的临界弯矩也偏差很小。

3 C1、C2、C3的简化

3.1 C1、C2、C3的拟合

将式（9）代入式（18）～（20），式（11）代入式（21），可得式（40）～（43）为

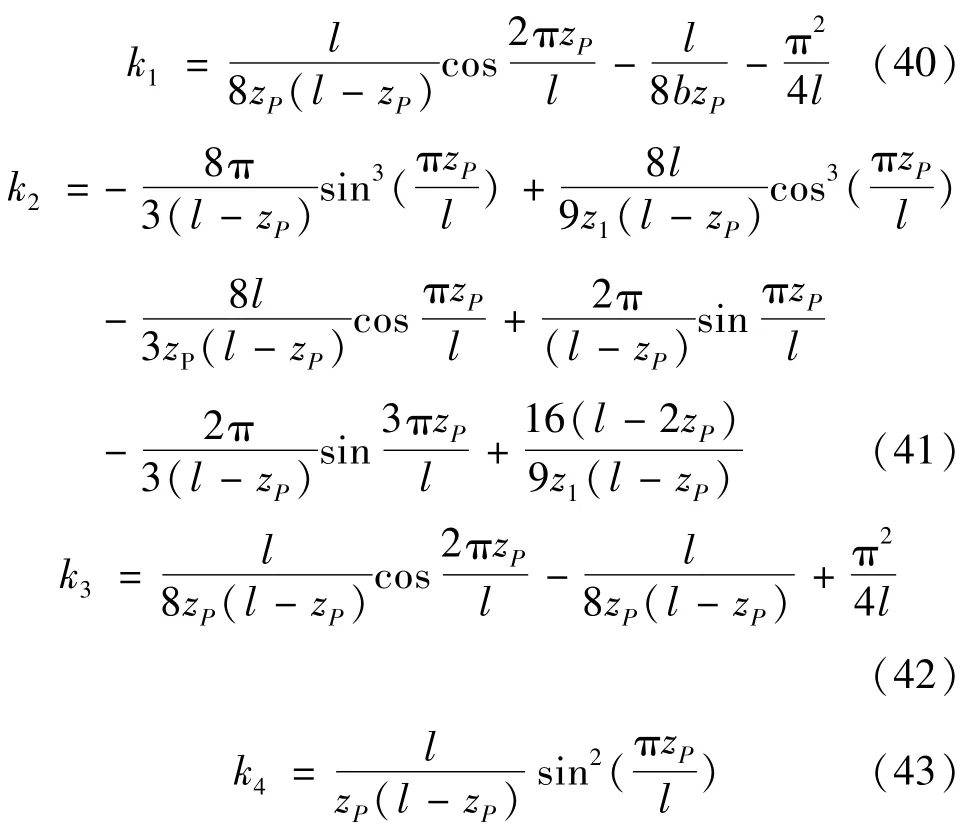
由式（40）～（43）可以看出，k1～k4的计算公式较为复杂，使得公式（34）～（36）的计算比较困难，不方便实际应用。为简化计算，文章利用简支梁的对称性，在（0，l／2］区间上等分的取十个点，由式（40）～（43）分别求出每个点处 C1、C2、C3的具体值，见表1。然后通过函数拟合，得出C1、C2、C3简化的计算方法。zP－C1、zP－C2、zP－C3之间的函数关系曲线如图2所示。图2中的三条曲线分别拟合成式（44）～（46）为

表 1 利用式（40）～（43）计算的 C1、C2、C3值

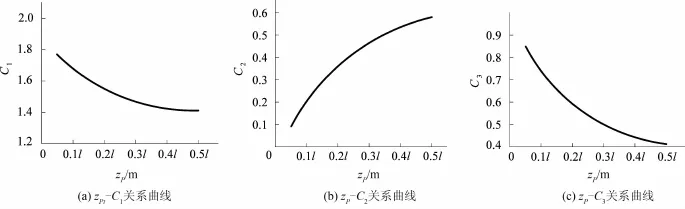
图 2 zP－C1、zP－C2、zP－C3的关系曲线图

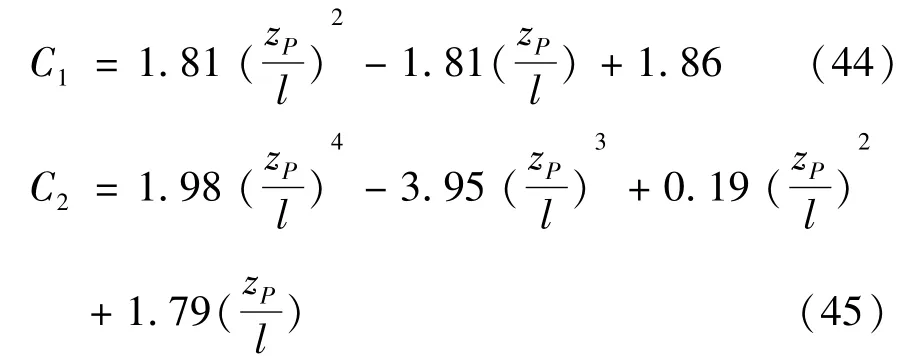
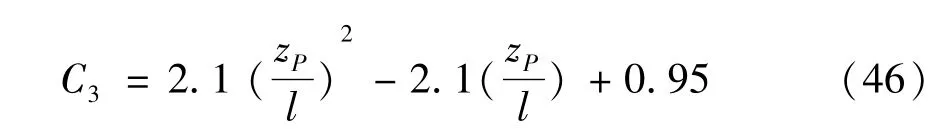
利用公式（44）～（46）求得的C1、C2、C3的值见表2。

对比表 1、2可得，相差最大的是 0.4l处C3的值，仅相差4.5%。

表 2 利用式（44）～（46）计算的 C1、C2、C3值

3.2 典型算例验证

如图3（a）所示简支梁，l为 9.0 m；采用双轴对称工字型截面，材料为Q235钢，截面尺寸如图3（b）所示。简支梁仅在 l／4处承担一个集中荷载 P，荷载作用于剪心 S，即 a＝0。图3中，zP表示荷载作用点距简支梁端的距离，m；l表示简支梁长度，m；S、O分别为截面的剪心和形心。

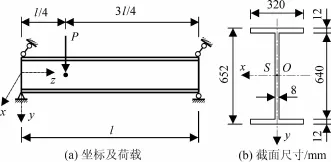
图3 l／4处作用一个集中荷载的单向受弯简支梁

由图3（b）可得构件的截面特性为：Iy＝6.56× 107mm4、Iω＝6.97×1012mm6、It＝6.29×105mm4；而Q235钢有 E＝2.06×105N／mm2、G＝0.79×105N／mm2；由式（41）～（43）可得C1＝1.52、C2＝0.41、C3＝0.56。将以上数据代入式（19）可得 Mcr＝921.95 kN·m。经典解［17］为 Mcr＝879.49 kN·m，误差仅为4.8%。因此，式（41）～（43）较为合理。

4 结论

文章基于 Bleich的总势能公式，通过瑞利—里兹法进行了一系列推导，给出了单个集中荷载作用于任意位置时简支梁临界弯矩的计算方法，并得出以下结论：

（1）文章所给公式适用于单个集中荷载作用于简支梁任意位置时的情况，适用范围相对较广。

（2）通过函数拟合简化了参数 C1、C2、C3的计算公式，方便使用。

（3）算例中，所给公式的计算结果与传统计算方法所得结果最大偏差仅为5.4%，表明文章所给公式仍具有较高的精度。

文章所给公式也有其局限性：采用 Bleich的总势能公式进行推导，未考虑童根树、吕烈武等对总势能公式的修正；也未能给出多个集中荷载作用下及复合荷载作用下简支梁临界弯矩的通用公式，这也是未来研究工作的方向。

［1］ Andrade A.，Camotimb D..Costa P providência e，on the evaluation of elastic critical moments in doubly and singly symmetric isection cantilevers［J］.Journal of Constructional Steel Research，2007，63（7）：894－908.

［2］ Challamel N.，Wang C.M..Exact lateral-torsional buckling solutions for cantilevered beams subjected to intermediate and end transverse point loads［J］.Thin-Walled Structures，2010，48（1）：71－76.

［3］ 罗金辉，顾强，方有珍.端弯矩及横向均布荷载共同作用下钢梁的整体稳定研究［J］.钢结构，2009，24（ST1）：148－152.

［4］ 秦桦，郭成喜.单轴对称工字形截面悬臂钢梁在横向荷载作用下的整体稳定性研究［J］.工程力学，2009（9）：152－155.

［5］ 杨波.工字梁在弯矩和均布荷载作用下的整体稳定［J］.钢结构，2012，27（11）：23－25.

［6］ 周芬，池云祥，杜运兴.上下翼缘同时受荷的工字形钢梁整体稳定性分析［J］.湖南大学学报（自然科学版），2012，39（11）：7－12.

［7］ GB 50017—2003，钢结构设计规范［S］.北京：中国计划出版社，2003.

［8］ 童根树.钢梁稳定性再研究：中国规范的演化及其存在问题（I）［J］.工业建筑，2014，44（1）：149－153.

［9］ Bleich F..Buckling Strength of Metal Structures［M］.New York：McGraw－Hill，1952.

［10］童根树.钢结构的平面外稳定（修订版）［M］.北京：中国建筑工业出版社，2013.

［11］吕烈武，沈世钊，沈祖炎，等.钢结构构件稳定理论［M］.北京：中国建筑工业出版社，1983.

［12］Kirby P.A.，Nethercot D.A..Design for Structural Stability［M］.Suffolk：Constrado Monographs，1979.

［13］陈绍蕃.有约束梁的整体稳定［J］.钢结构，2008，23（8）：20－ 25.

［14］周绪红，刘占科，陈明，等.钢梁弯扭屈曲临界弯矩通用公式研究［J］.建筑结构学报，2013，34（5）：80－86.

［15］刘占科，周绪红，何子奇，等.复合荷载作用下简支钢梁弹性弯扭屈曲研究［J］.建筑结构学报，2014，35（4）：78－85.

［16］Clark J.W.，Hill H.N..Lateral buckling of beams［J］.Journal of Structural Division，The American Society of Civil Engineers，1960，86（ST7）：175－196.

［17］陈骥.钢结构稳定理论与设计（第6版）［M］.北京：科学出版社，2014.

Elastic critical moment of simply supported beams under a moving concentrated load

Chu Hao，Guo Bing*，Guan Hailong
（School of Civil Engineering，Shandong Jianzhu University，Jinan 250101，China）

The critical moment design formula of simply supported beam has its specific scope of application，and the design formula of a single concentrated load is applicable only to special positions，while the result of load acting on other positions is large deviation.Based on Bleich’s total potential formula，the article assumed that any functions of bending and torsion deformation and bending moment diagram can be simulated，conducted the research on the critical moment of simply supported beam focusing on single concentrated load，analyzed critical moment design formula of single concentrated load in any position，put forward simplified calculation method for relevant parameters in formula，meanwhile made illustrative examples and verified accuracy of formula.The result turned out that the given critical moment design formula is capable of calculating critical moment design formula of single concentrated load in any position；the formula is consistent with traditional formula，the parameters C1，C2，C3are not specific values，but expressed in calculation formula，the scope of application is broader.In the case study，the maximum deviation of given formula calculation result and traditional calculation method is simply 5.4%.

simply supported beam；single moving load；elastic critical moment；Rayleigh-Ritz method

TU391

A

1673－7644（2016）05－00466－05

2016－07－01

禇昊（1991－），男，在读硕士，主要从事钢结构稳定等方面的研究.E-mail：36510485＠qq.com

*：郭兵（1970－），男，教授，博士，主要从事钢结构稳定及抗震等方面的研究.E-mail：sdgb123＠163.com