静止坐标系下LCL型并网逆变器控制策略的研究

屈克庆，叶天凯，赵晋斌，李文旗（上海电力学院电气工程学院，上海200090）



静止坐标系下LCL型并网逆变器控制策略的研究

屈克庆，叶天凯，赵晋斌，李文旗
（上海电力学院电气工程学院，上海200090）

摘要：通过分析三相LCL型并网逆变器在两相静止坐标系下的数学模型，提出了一种静止坐标系下利用准比例谐振（proportional resonant，PR）控制器实现入网电流无静差跟踪的控制策略。为了有效抑制LCL滤波器由于阻尼不足而产生的谐振，引入电容电流反馈来实现有源阻尼。采用频域分析法，根据稳定性、稳定裕度以及稳态误差要求，分别设计电容电流反馈系数及准PR控制器的比例系数和谐振增益系数。仿真与实验结果验证了所采用参数设计方法的正确性和所提出控制策略的可行性。

关键词：LCL滤波器；准PR控制器；有源阻尼；电容电流反馈

随着电力电子变换技术的迅速发展，新能源并网发电成为解决能源危机、温室效应等问题的有效手段［1-2］。以脉宽调制（PWM）技术为基础的电压源型逆变器（VSI）以其输出入网电流正弦度高，且功率因数可控等优点，得到广泛应用。

VSI通常采用PWM技术，其输出电流中含有高次谐波，无法满足并网要求。因此，VSI输出与电网间需要接入滤波器，常用L和LCL两种类型滤波器。LCL滤波器与L滤波器相比有更理想的高频滤波效果，且体积和损耗均小于同等滤波效果的L滤波器。然而，LCL滤波器为高阶系统，增加了控制器的设计复杂度。而且，LCL滤波器存在谐振问题，影响系统稳定性能［3-7］。为了抑制LCL滤波器的谐振特性，提高系统稳定性，常用无源阻尼法和有源阻尼法。无源阻尼法通过在滤波器的回路中串入电阻来增加系统的阻尼，这样会增加系统损耗，降低系统效率。为此，学者提出了多种有源阻尼控制策略，主要包括机侧电感电流反馈法，电容电流反馈法，分裂电容法及零极点配置等［8-11］。

根据参考坐标系的不同，VSI控制器可分为基于静止自然坐标系和基于旋转同步坐标系两类［12-14］。在同步坐标系下，三相交流量经过abc/ dq坐标变换转换为直流量，然后采用传统比例积分（PI）控制器实现无静差控制。但坐标变换引入复杂的耦合问题，解耦控制方法复杂；而且需要锁相环来提供变换所需相角。在静止坐标系下，PR控制器能在特定频率处发生谐振，并且在这一频率点具有无穷大的控制增益，因而可实现对特定频率点正弦信号的无静差控制。然而，模拟系统元器件参数精度和数字系统精度限制了理想PR控制器的实现。另外，理想PR控制器在非基频处增益非常小，当电网频率产生偏移时，就无法有效抑制电网产生的谐波。因此，在理想PR控制器的基础上提出了一种易于实现的准PR控制器［15-16］。准PR控制器阶数高、参数多，故其控制参数的选取至关重要。

本文提出了一种静止坐标系下利用准PR控制器实现入网电流无静差跟踪的控制策略。为了有效抑制LCL滤波器由于阻尼不足而产生的谐振，引入电容电流反馈来实现有源阻尼。采用频域分析法，根据开环系统稳定性、稳定裕度以及稳态误差要求，分别设计电容电流反馈系数及准PR控制器的比例系数和谐振增益系数。仿真与实验结果验证了所采用参数设计方法的正确性和所提出控制策略的可行性。

1　系统建模

图1所示为三相LCL型并网VSI的主电路。图1中，6个开关管VT1～VT6组成三相逆变桥；Vdc为直流侧电压；L1，C，L2构成LCL滤波器。设定直流侧电压保持恒定且忽略电感电容寄生电阻。各矢量方向如图1中标注所示，容易得到在αβ两相静止坐标下，系统模型结构如图2所示。

图1　三相LCL型并网VSI主电路Fig.1 VSI main circuit of three-phase gridconnected inverter with LCL filter

图2　两相静止坐标下系统结构框图Fig.2 Model structure diagram of system in two-phase stationary coordinates

由图2得到入网电流i2αβ与逆变桥输出电压u1αβ之间的传递函数为

式（1）所示系统由1个一阶积分环节与1个阻尼系数为零的二阶振荡环节串联组成。因此，由于系统欠阻尼，必然出现谐振。为了有效抑制谐振，可采用反馈系数为K的电容电流ic反馈来增大系统阻尼。其结构框图如图3所示，其中KPWM为逆变器等效比例环节，忽略死区和控制延时，KPWM=1。

图3　带电容电流反馈的系统结构框图Fig.3 Model structure diagram of system with capacitor current feedback

由图3得到系统传递函数为

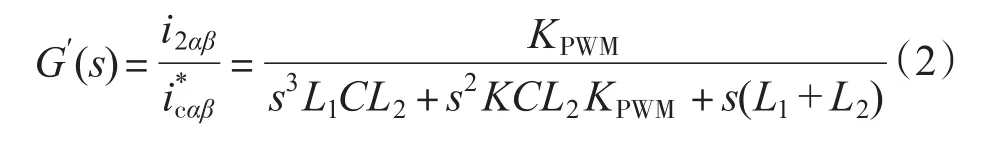
2　控制器选择

在静止坐标系下，理想PR控制器能在特定频率处发生谐振，实现对特定频率点正弦信号的无静差控制。然而，理想PR控制器难以实现。本文采用在理想PR控制器的基础上提出的一种易于实现的准PR控制器，其传递函数为

式中：ω0为准PR控制器的谐振频率；ωc为谐振频率处的谐振带宽；KP为比例系数；KR为谐振增益系数。

选定KR=10，KP=1，图4所示为理想PR控制器及准PR控制器在不同谐振带宽ωc值时的伯德图。由图4可知，准PR控制器即可以保持理想PR控制器在谐振频率点的高增益，同时还可以通过调整谐振带宽ωc来有效减小谐振频率偏移对控制系统性能的影响。

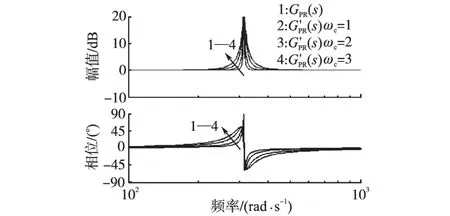
图4　理想PR控制器及准PR控制器不同ωc时的伯德图Fig.4 Bode plot of idea PR controller and quasi-PR controller with different ωc

选定KR=50，ωc=3，KP变化时的伯德图如图5所示。分析可知，KP主要决定非谐振频率处增益，KP的值越大，非谐振频率处的增益越大。选定KP=10，ωc=3，KR变化时的伯德图如图6所示。分析可知，KR主要决定谐振频率处增益，KR的值越大，谐振频率处的增益越大。

图5　不同KP值时准PR控制器伯德图Fig.5 Bode plot of quasi-PR controller with different KP

图6　不同KR值时准PR控制器伯德图Fig.6 Bode plot of quasi-PR controller with different KR

3　控制器参数整定

由以上分析可以得到图7所示的系统简化控制框图，得到控制系统开环传递函数

式（4）表明，系统开环传递函数由两部分组成：代表准PR控制器的G′PR(s)和除去入网电流外环外的系统模型G′(s)。根据系统开环稳定性、稳定裕度和稳态误差的要求，对电容电流反馈系数K、准PR控制器谐振增益系数KR及比例系数KP进行整定。

图7　系统控制简化控制框图Fig.7 Simplified control block diagram of system

系统稳定性由截止频率ωcc附近的频域特性决定，通过选择适当的滤波器及控制器参数可以使系统截止频率ωcc远离准PR控制器的谐振频率ω0。由准PR控制器的伯德图可知，除谐振频率ω0外，准PR控制器与系数为KP的比例控制器有相同的特性。于是，在进行稳定性分析时，准PR控制器可由比例系数为KP的比例控制器近似。简化后的系统开环传递函数可以表示为

由式（5）可知，简化后的开环系统由1个一阶积分环节、1个振荡环节和1个比例环节组成。根据典型环节近似幅频特性作出简化后系统开环近似幅频特性曲线如图8所示。

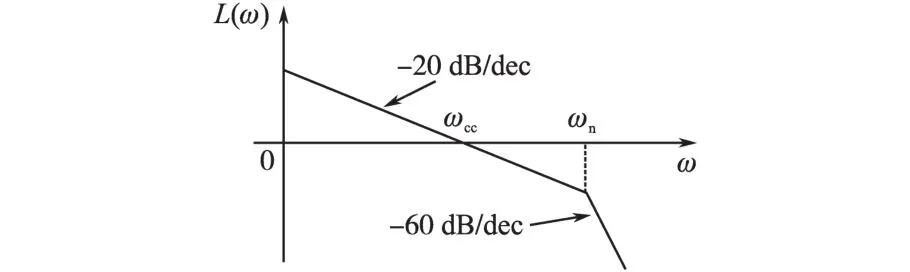
图8　简化后系统开环近似幅频特性Fig.8 Approximated open-loop amplitude frequency characteristics of system

图8中，ωcc为开环系统截止频率，ωn为振荡环节转折频率，根据频域理论有

振荡环节阻尼系数

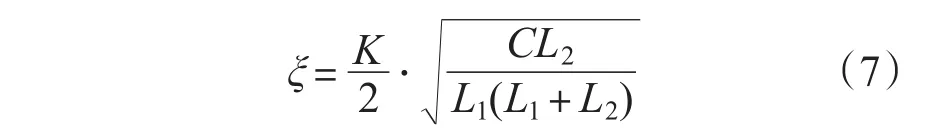
截止频率ωcc决定开环系统相位裕度，ωcc距离转折频率ωn越远，相位裕度越大；振荡环节阻尼系数ξ决定转折频率ωn处的幅值增益，ξ越大，转折频率处的幅值增益越小，开环系统幅值裕度越大，但是系统相位裕度越小。因此，为保证系统稳定性且有足够的稳定裕度，可按如下次序进行控制器参数整定。

1）根据稳定性要求整定准PR控制器比例系数KP。

开环系统稳定应满足

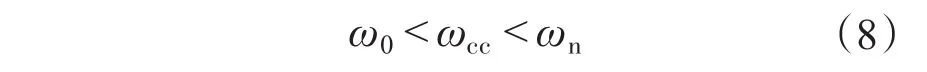
得到

选择滤波器参数为：L1=2 mH，C=20 μF，L2= 1 mH，得到0.94＜KP＜25.98。考虑一定的稳定裕度，可选择KP=12。

2）根据稳定裕度要求整定电容电流反馈系数K。

内环反馈系数K决定振荡环节阻尼系数，图9所示为选定滤波器参数及KP后，阻尼系数ξ在0.3 到0.8之间变化时，简化系统G′(s)的开环伯德图。选择阻尼系数ξ=0.7，得到K=24.26，本文选择K=25。

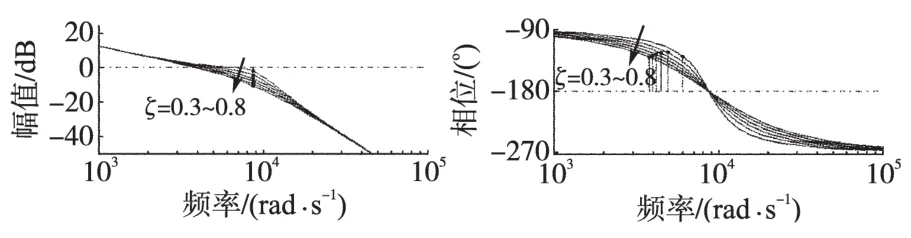
图9　不同ξ时系统开环伯德图Fig.9 Open-loop Bode plot of system with different ξ

3）根据电网频率波动范围整定准PR控制器谐振带宽频率ωc。

国家标准GB/T15945—1995规定电力系统正常的频率标准为（50±0.2）Hz，保留一定的裕度，选择ωc=3。

4）根据基频ω0处幅值增益要求整定准PR控制器谐振增益系数KR。

开环传递函数在基频ω0处幅值增益越大，系统稳态误差越小。将s=jω0代入式（4）中，得到基频处幅值增益为

为保证系统稳态误差满足要求，设定基频开环增益为60 dB，得到KR=931.4，考虑一定的裕度，本文选择KR=950。

根据以上设计参数画出系统开环伯德图如图10所示。由图10可得到，系统截止频率为3 920 rad/s，开环幅值裕度为9.18 dB，相位裕度为43.7°，基频处幅值增益为60.2 dB。这表明按以上设计方法得到的参数能够保证系统稳定性，且满足性能要求。

图10　系统开环伯德图Fig.10 Open-loop Bode plot of system

4　仿真与实验

为验证所提出控制方案的有效性和参数设计方法的正确性，在Matlab/Simulink软件中进行了仿真。仿真参数为：emax=380 V，Vdc=700 V，fPWM= 5kHz，ω0=100π·rad/s，SN=10kV·A，L1=2mH，C=20 μF,L2=1mH,KP=12,KR=950,K=25,ωc=3 rad/s。

图11所示为给定有功功率为38 kW（输出入网电流幅值为100 A）时，逆变器a相输出电流及电网a相电压波形。可以看出，此时电网电压与入网电流同相位。a相入网电流谐波分析结果如图12所示，THD=1.61%，满足并网要求。输出有功功率、无功功率以及功率因数如图13所示，整个系统在1个工频周期后达到稳定，输出功率跟踪给定值，给定无功为零时，功率因数为1。

图11　a相电网电压及a相入网电流仿真波形Fig.11 Simulation waveforms of a-phase grid voltage and output current

图12　a相入网电流THD分析结果Fig.12 THD analysis result of a-phase output current

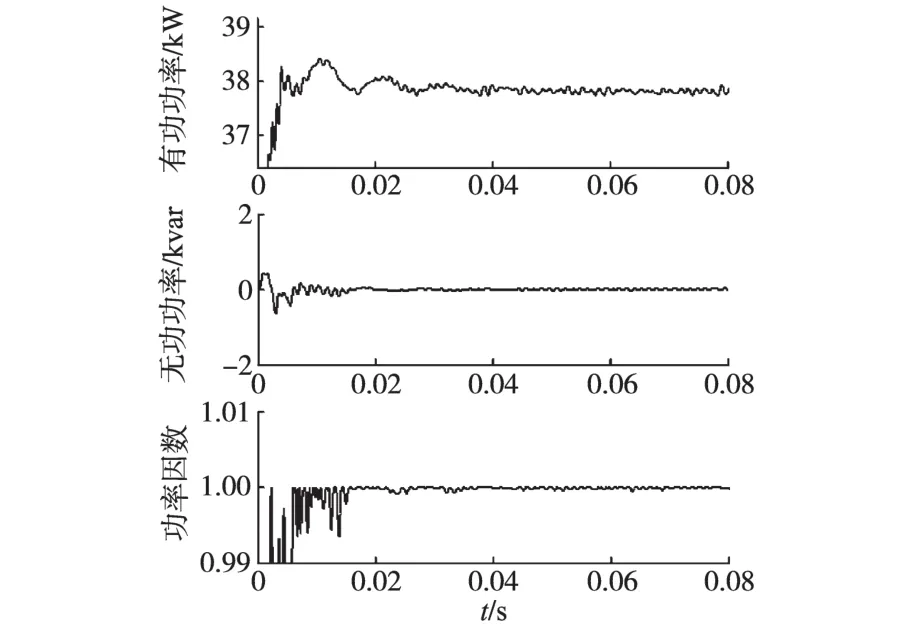
图13　输出有功功率、无功功率及功率因数仿真结果Fig.13 Simulation results of output active power，reactive power and power factor

为验证所提出方案的动态性能，在0.1 s时将有功功率给定值由38 kW阶跃变化为19 kW，同时无功功率给定值保持为零，a相输出电流及a相电网电压波形如图14所示。可以看出，a相电流在很短的时间内就完成了对给定值的跟踪，且仍与a相电网电压保持同相位，保持单位功率因数。

基于以上分析及仿真验证，在1台额定功率为3 kW的实验样机上进行了实验验证。采用可编程电源模拟三相电网，可编程PV直流电源作为直流侧电源，其他参数与仿真条件一致。图15所示为给定有功功率为1.5 kW（输出入网电流幅值为15 A）时，逆变器a相输出电流及电网a相电压实验波形。可以看出，输出电流与电网电压同相位，实验结果与理论分析及仿真结果一致。

图14　给定有功阶跃变化时a相入网电流仿真结果Fig.14 Simulation results of a-phase output current when the set value of active power step change

图15　a相电网电压及a相入网电流实验波形Fig.15 Experiment waveforms of a-phase grid voltage and output current

给定有功功率发生变化前后，逆变器a相输出电流及电网a相电压实验波形分别如图16a、16b所示。可以看出，输出入网电流能实现对给定值的有效跟踪，且入网电流与电网电压仍保持同相位，满足功率因数为1的要求。

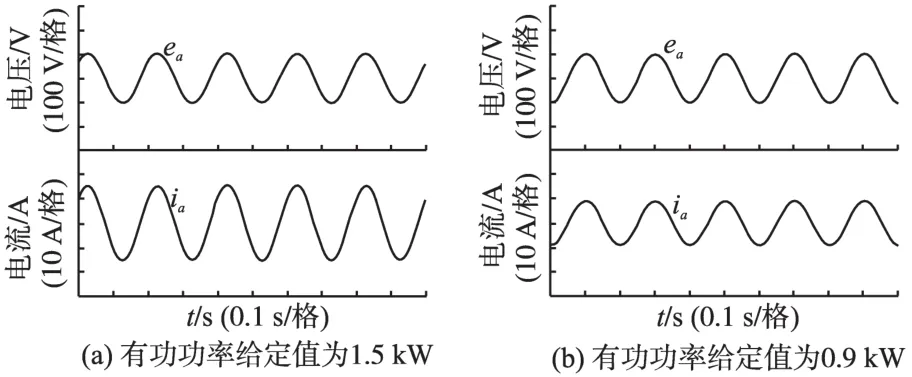
图16　给定有功变化时实验波形Fig.16 Experiment waveforms when the set value of active power change

5　结论

本文提出了一种静止坐标系下利用准PR控制器实现三相LCL型并网逆变器入网电流无静差跟踪的控制策略。引入电容电流反馈来实现有源阻尼，有效抑制了LCL滤波器由于阻尼不足而产生的谐振。采用频域分析法，根据开环系统稳定性、稳定裕度以及稳态误差要求，分别设计了电容电流反馈系数及准PR控制器的比例系数和谐振增益系数。仿真与实验结果表明所提出的控制策略有良好的动、静态性能，具有高质量入网电流、输出功率可控以及单位功率因数的优点。

参考文献

［1］Han T，Ansaru N. On Optimizing Green Energy Utilization for Cellular Networks with Hybrid Energy Supplies［J］. Wireless Communications，IEEE Transactions on，2013，12（8）：3872-3882.

［2］Guangqian D，Feng G A O，ZHANG S，et al. Control of Hybrid AC/DC Microgrid Under Islanding Operational Conditions［J］. Journal of Modern Power Systems and Clean Energy，2014，2 （3）：223-232.

［3］周国华，许建平.开关变换器调制与控制技术综述［J］.中国电机工程学报，2014，34（6）：815-831.

［4］孙绍华，李春鹏，贲洪奇.采用LCL滤波的三相并网逆变器［J］.电工技术学报，2011，26（S1）：108-112.

［5］Tang Y，Loh P C，Wang P，et al. Exploring Inherent Damping Characteristic of LCL-filters for Three-phase Grid-connected Voltage Source Inverters［J］. Power Electronics，IEEE Trans⁃actions on，2012，27（3）：1433-1443.

［6］白志红，阮新波，徐林.基于LCL滤波器的并网逆变器的控制策略［J］.电工技术学报，2011，26（S1）：118-124.

［7］王要强，吴凤江，孙力，等.带LCL输出滤波器的并网逆变器控制策略研究［J］.中国电机工程学报，2011，31（12）：34-39.

［8］刘飞，段善旭，查晓明.基于LCL滤波器的并网逆变器双环控制设计［J］.中国电机工程学报，2009，29（S1）：234-240.

［9］沈国桥，徐德鸿. LCL滤波并网逆变器的分裂电容法电流控制［J］.中国电机工程学报，2008，28（18）：36-41.

［10］徐志英，许爱国，谢少军.采用LCL滤波器的并网逆变器双闭环入网电流控制技术［J］.中国电机工程学报，2009，29（27）：36-41.

［11］Malinowski M，Bernet S. A Simple Voltage Sensorless Active Damping Scheme for Three-phase PWM Converters with an LCL Filter［J］. Industrial Electronics，IEEE Transactions on，2008，55（4）：1876-1880.

［12］Loh P C，Holmes D G. Analysis of Multiloop Control Strategies for LC/CL/LCL-filtered Voltage-source and Current-source In⁃verters［J］. Industry Applications，IEEE Transactions on，2005，41（2）：644-654.

［13］Khajehoddin S A，Karimi-Ghartemani M，Jain P K，et al. A Control Design Approach for Three-phase Grid-connected Re⁃newable Energy Resources［J］. Sustainable Energy，IEEE Transactions on，2011，2（4）：423-432.

［14］Bao X，Zhuo F，Tian Y，et al. Simplified Feedback Lineariza⁃tion Control of Three-phase Photovoltaic Inverter with an LCL Filter［J］. Power Electronics，IEEE Transactions on，2013，28 （6）：2739-2752.

［15］吕永灿，林桦，杨化承，等.基于多谐振控制器和电容电流反馈有源阻尼的PWM变换器电流环参数解耦设计［J］.中国电机工程学报，2013，33（27）：44-51.

［16］郭强，刘和平，彭东林，等.静止坐标系下电流型PWM整流器电流环控制策略研究及其参数设计［J］.中国电机工程学报，2014，34（15）：2353-2361.

修改稿日期：2015-09-02

Study on a Control Strategy in a Stationary Frame for Grid-connected Inverter with LCL Filter

QU Keqing，YE Tiankai，ZHAO Jinbin，LI Wenqi
（Institute of Electrical Engineering，Shanghai University of Electric Power，Shanghai，200090，China）

Abstract:Through analysis of the mathematical model of three-phase grid-connected inverter with LCL filter in the two-phase stationary coordinates，a quasi-PR controller based grid current astatic tracking control strategy was proposed. To restrain the resonance due to insufficient damping，the capacitor current feedback was introduced to realize active damping. According to the requests of stability，stability margin and steady-state error，the capacitor current feedback coefficient，the resonant gain and proportional factor of quasi-PR controller could be designed respectively by the using of frequency theory. The effectiveness of adopted parameters design method and feasibility of proposed control strategy are verified by the simulation and experiment results.

Key words:LCLfilter；quasi-PR（proportionalresonantcontroller）；activedamping；capacitorcurrentfeedback

收稿日期：2015-05-09

作者简介：屈克庆（1970-），男，博士（后），副教授，硕士生导师，Email：kqqu@shiep.edu.cn

基金项目：上海市绿色能源并网工程技术研究中心（13DZ2251900）

中图分类号：TM615

文献标识码：A