新型PWM整流器预测直接功率控制研究

郑宏，王哲禹，黄俊，张云（1.机械工业设施农业测控技术与装备重点实验室，江苏镇江1013；.江苏大学电气信息工程学院，江苏镇江1013）

Pref,Qref是有功功率和无功功率的参考值。传统PDPC指标函数是由有功功率和无功功率误差的平方和构成［9］，控制目标是使每个控制周期内功率误差最小，因此定义指标函数为

每个控制周期选择一个非零矢量与零矢量，以指标函数最小为约束条件，即矢量作用时间满足：



新型PWM整流器预测直接功率控制研究

郑宏1，2，王哲禹2，黄俊2，张云2
（1.机械工业设施农业测控技术与装备重点实验室，江苏镇江212013；2.江苏大学电气信息工程学院，江苏镇江212013）

摘要：介绍了预测直接功率控制原理以及电压矢量选择原则。传统的预测直接功率控制方法中，有功功率和无功功率均由同一个指标函数控制，所以当PWM整流器的一个控制量受到扰动，另一个控制量也会受到干扰，进而引起整流器变量间的相互干扰，导致PWM整流器动态性能和稳定性下降。提出一种新型的预测直接功率控制方法，即通过设置权衡因子来重新设置指标函数，以减少功率发生变化时，因控制量间的相互干扰对整流器造成的影响。通过Matlab/Simulink的仿真结果和多功能实验平台样机的实验结果证明，与传统的预测直接功率控制相比，本方法有更好的动态性能与鲁棒性。

关键词：PWM整流器；直接功率控制；预测控制；指标函数

PWM整流器广泛应用于直流电源、电机调速、有源电力滤波、无功补偿、超导储能、高压直流输电、统一潮流控制器、太阳能发电等领域［1］。由于PWM整流器及其控制技术有广泛的应用前景，备受学术界关注，近年来相继有很多新的整流器控制方法被提出：滑模变结构控制［2］、模糊控制［3］、二次最优控制、预测控制［4］等。预测直接功率控制是将直接功率控制（DPC）与预测控制相结合，具有良好的稳态性能和快速的动态响应。其原理是先预测下一个控制周期的功率，再计算预测与参考功率的误差，最后通过有功功率和无功功率的平方和构建指标函数，选择最佳矢量，并计算出矢量的作用时间。由于是对下一个周期的功率误差进行预测，因此相比于传统的直接功率控制，PDPC的精确度和效率更高，还具有鲁棒性强、固定开关频率等优点［5］。

传统PWM整流器PDPC由于2个变量（有功功率和无功功率）均由同一个指标函数控制［6］，当其中的一个变量发生大的变化时，由于控制权会集中到变量发生变化的一侧，使另一侧控制力下降，导致控制权失衡，产生相互干扰，使整流器动态性能下降。本文在指标函数中设置权衡因子，保持控制权平衡，抑制变量间相互干扰，提高整流器性能。

1　PWM整流器预测功率控制模型

1.1. PWM整流器PDPC模型

三相PWM整流器的拓扑结构，如图1所示。

图1　三相PWM整流器拓扑结构Fig.1 Topology of the three-phase PWM rectifier

由于是Y型无中线结构不存在零序分量。其在两相旋转坐标系（d，q）下的表达式为

式中：ω为电网基波角频率；ed,eq为电源电压；vd,vq为整流器交流侧输出电压；id,iq为交流侧输入电流；L为滤波电感；R为线路电阻。

从旋转坐标系下复功率S=P+jQ=1.5(E·I*)得到：

在两相旋转坐标系下ed,eq为常数，将式（2）带入式（1）并求导得到：

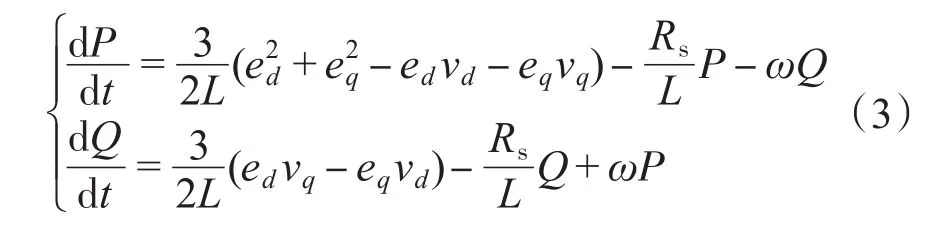
由式（4）可知，下一个检测周期的有功功率P和无功功率Q的预测值表达式为

式（4）的功率预测算法控制PWM整流器存在控制延时问题，引起功率的控制误差［7-8］。因此提出了采用预测(k+2)时刻的功率值来替代(k+1)的功率，以此解决控制延时带来的影响。首先通过式（4）求出(k+1)时刻的功率值，进而通过下式求出(k+2)时刻的预测功率值。

传统PDPC的每个控制周期TS结束时，功率的误差EP,EQ为

Pref,Qref是有功功率和无功功率的参考值。传统PDPC指标函数是由有功功率和无功功率误差的平方和构成［9］，控制目标是使每个控制周期内功率误差最小，因此定义指标函数为

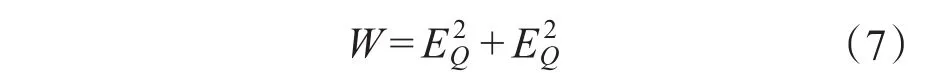
每个控制周期选择一个非零矢量与零矢量，以指标函数最小为约束条件，即矢量作用时间满足：

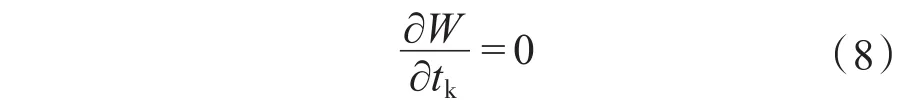
1.2 DPC开关表

图2是三相两电平PWM整流器的空间矢量图，6个非零矢量将正六边形划分为6个相等的扇区，零矢量位于正六边形的中心［10］。

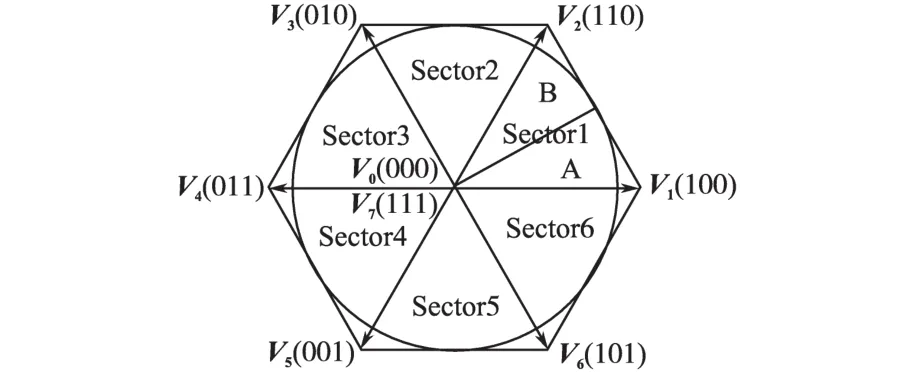
图2　三相PWM整流器电压空间矢量图Fig.2　 Voltage vectors of three-phase PWM rectifier

根据式（3）和第3节仿真实验的系统参数，当整流器在单位功率因数下运行时，在不同的电压矢量作用下，随着ω的变化，有功功率变化率dP/dt和无功功率斜率变化率dQ/dt的波形，如图3所示。以此总结出PDPC的功率开关表如表1所示。

表1　PDPC开关表Tab.1 Switching table of PDPC

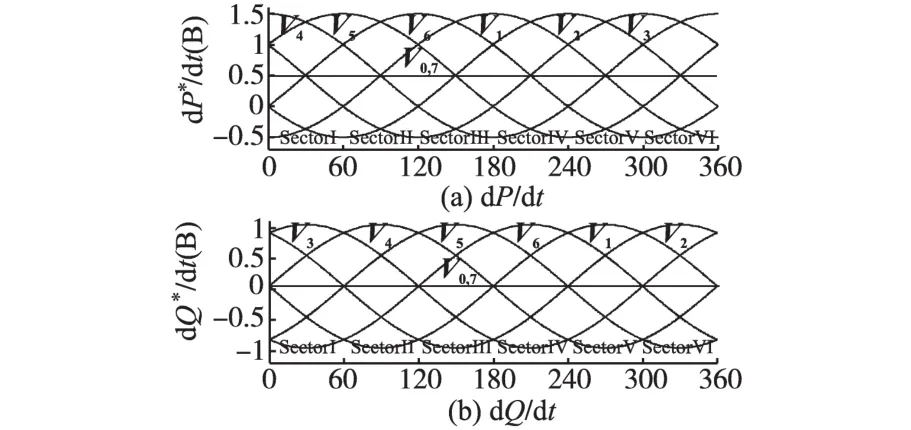
图3　各电压矢量对应dP/dt,dQ/dt波形Fig.3 Diffeerent vector versus waveforms of dP/dt,dQ/dt

预测直接功率控制的矢量选择，应根据功率误差的值和所处扇区进行选择。表1中可以看到P↑Q↑的情况下有3种选择，P↑Q↓的情况下有2种选择，但各矢量变化率大小不同。如图3所示，将扇区1平均划分为A，B两部分。根据图3及式（3）可知，P↑Q↑，P↑Q↓不同矢量对有功功率和无功功率变化率的大小如表2所示。

表2　不同矢量对P,Q影响力大小Tab.2 Different vector influence on P,Q

2　改进的预测直接功率控制

传统预测直接功率控制方法，其有功功率和无功功率控制变量均由同一个指标函数控制。当遇到较小的扰动时，变量间相互之间的干扰较小。若整流器扰动较大或功率发生巨大变化，变量间相互的干扰很大，其控制权会集中到一侧，导致另一个变量的控制力下降。因此本文通过引入权衡因子重新设置指标函数，以此来解决功率剧烈变化所引起相互干扰的问题，提高整流器的动态性能和鲁棒性。其控制原理如图4所示。

教育部2011年修订的《全日制义务教育数学课程标准》中明确提出“四基”，即学生的“基本知识、基本技能、基本思想、基本活动经验”。本次修改相对于2001年的实验稿有了一个重大变化，即是在 “双基”上增加了基本思想和基本活动经验。

图4　PWM整流器PDPC控制原理图Fig.4 Control principle diagram of proposed PDPC

2.1最佳空间矢量的确定

预测控制是一种基于模型的闭环优化控制策略，具有控制效果好、鲁棒性强等优点，可有效地克服过程的不确定性、非线性和并联性，并能方便处理过程被控变量和操纵变量中的各种约束。指标函数主要任务是跟踪控制系统中特定的变量，在下一个控制周期，使指标函数值达到最小的控制方式，实现最优控制。预测控制的系统变量、约束条件和预测要求均可应用于指标函数。这使得预测控制更容易控制系统，进而提高系统效率、安全性和电能质量。由于整流器两个变量间的耦合关系，以及应用同一个指标函数所导致的在遇到大的扰动时控制权集中到一个变量，导致对另一个变量的控制力变弱，造成相互干扰。本文基于预测直接功率控制，在指标函数中引入权衡因子，通过对权衡因子的调节，提高整流器动态性能。其重置指标函数如下式所示：

式中：Pwf,Qwf为权衡因子。

首先根据式（9）选择合适的电压矢量，指标函数选择的电压矢量需要满足使功率误差变为最小的要求。在这一过程中如果功率误差变化不大，由于变量间的相互干扰比较小，可以不考虑指标函数的权衡因子。而在功率变化剧烈的大功率系统中，由于变量之间相互干扰作用大，控制权会集中到一个变量上，导致系统对另一个变量控制力下降，导致PWM整流器性能降低，此时需要考虑权衡因子。

指标函数中的权衡因子可以根据功率误差EP,EQ的幅值大小来调节自身Pwf,Qwf的幅值，进而平衡的分配控制权。通过权衡因子可以减弱因功率剧烈变化所导致的变量间的相互干扰，进而提高整流器动态性能。权衡因子表达式为

式中：SB为PWM整流器复功率的基准值；N为比例因子，来调节权衡因子幅值大小，满足整流器控制需求。

当有功功率剧烈变化时，无功功率控制权Qwf迅速增大，而Pwf相对较小，以此补偿无功功率的动态性能控制；反之，当无功功率剧烈变化时，有功功率控制权Pwf增大，而Qwf相对较小，以此补偿有功功率的动态性能。

传统直接功率控制仅用单个非零矢量进行调节，而本文的PDPC同时应用非零矢量与零矢量，通过调节两种矢量的占空比来满足系统的功率需求。首先根据系统所在扇区选择最佳空间矢量，然后通过功率误差最小原则对各矢量工作时间进行计算。设Pk和P0是非零矢量Vk与零矢量有功功率变化率，Qk和Q0是非零矢量Vk与零矢量无功功率变化率（变化率通过式（3）可得，如图3所示），得到下式：

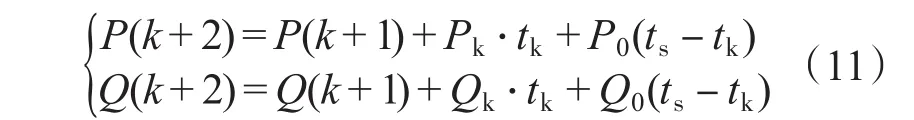
式中：ts为控制周期；tk为非零矢量作用时间；ts-tk为零矢量作用时间。tk应满足使指标函数最小的要求：

通过式（11），式（12）求得tk为

3　仿真与实验

本文首先应用Matlab/Simulink软件进行仿真验证，然后在电力电子多功能实验平台进行实验验证。整流器系统参数为：直流侧电压Udc= 500 V，线电压=380 V，额定有功功率P=1 kW，P= 10 kW，额定无功功率Q=0 kW，电感L=9 mH，电容C=3000 μF，采样频率=3 000 Hz，系统电压频率=50 Hz。开关频率3 kHz，PDPC开关表见表1。

图5分别是传统PDPC和加入权衡因子PDPC控制方法的仿真波形。无功功率设置为零，当t= 0.2 s有功功率从1 kW突变到10 kW，t=0.4 s有功功率从10 kW突变到1 kW。两图对比可知当发生功率突变时，传统PDPC的无功功率波动较大，达到新平衡的时间较长，而加入权衡因子的PDPC无功功率波动小，恢复平衡时间短。传统控制方法与本文提出方法的功率因数均接近于1，无过大差别。

图6是PWM整流器输入电流畸变率，本文提出PDPC的THD为1.25%，比传统方法低1.48%，电流畸变率小。图7是整流器直流侧电压波形，本文提出的加入权衡因子的PDPC在功率突变时，与传统PDPC相比电压波动小。

图8分别是无功功率为零，有功功率由1 kW突变到10 kW，再由10 kW变到1 kW时，波形由上到下依次为有功功率、无功功率，整流器输入电流、电网电压的实验波形。其实验结果与仿真结果一致，带有权衡因子的PDPC控制，在有功发生变化时，无功功率波动小，调整速度快。

图5　Matlab仿真波形Fig.5 Simulink waveforms of Matlab

图6　电流畸变率Fig.6　 THD% of current

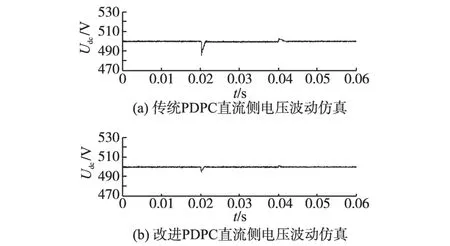
图7　直流侧电压波形Fig.7 Waveforms of DC side voltage

图8　PDPC实验波形Fig.8 Experiment waveforms of PDPC

图9为输入电流的THD%，传统PDPC的THD为5.97%，本文的THD%为2.61%。可见带有权衡因子的PDPC控制可以一定幅度地减少输入电流谐波。

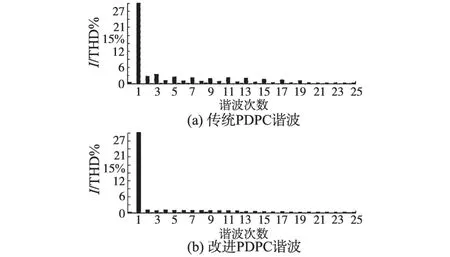
图9　电流THD%Fig.9 THD% of input current

可见本文的实验结果与仿真结果一致，带有权衡因子的PDPC控制，在有功功率变化时，无功功率波动小，功率响应速度快；但本文提出的方法THD略小，均可以在单位功率因数下运行。

4　结论

根据传统PDPC控制的不足，即功率变化时预测控制对两个变量的控制失去平衡，提出了加入权衡因子的方法，Matlab/Simulink仿真和电力电子多功能实验平台的实验结果证明加入权衡因子后，有功功率变化时，无功功率波动、直流侧电压波动小，恢复平衡时间短，PWM整流器性能得到提高。

参考文献

［1］罗悦华，伍小杰，王晶鑫.三相PWM整流器及其控制策略的现状及展望［J］.电气传动，2006，36（5）：3-8.

［2］刘波，申群太.三相电压型PWM整流器的滑模变结构控制［J］.自动化技术与应用，2010，29（4）：81-84.

［3］瞿博，洪小圆.模糊控制在三相PWM整流器无差拍控制中的应用［J］.中国电机工程学报，2009，18（15）：50-54.

［4］Eskandari-Torbati H，Khaburi D A. Direct Power Control of Three Phase PWM Rectifier Using Model Predictive Control and SVM Switching［J］. Power Electronics，Drive Systems & Technologies Conference，2013，16（6）：193-198.

［5］Hu J，Zhu J，Platt G，et al. Model-predictive Direct Power Con⁃trol of AC/DC Converters with One Step Delay Compensation ［J］. Conference of the IEEE Industrial Electronics Society，2012，2（1）：4892-4897.

［6］汪显博，卜文绍.三相电压型PWM整流器研究现状与发展趋势［J］.电源技术，2010，34（10）：1093-1097.

［7］Xia C，Wang M，Song Z，et al. Robust Model Predictive Cur⁃rent Control of Three-phase Voltage Source PWM Rectifier with Online Disturbance Observation［J］. Industrial Informat⁃ics IEEE Transactions on，2012，8（3）：459-471.

［8］Zhang Y，Li Z，Zhang Y，et al. Performance Improvement of Direct Power Control of PWM Rectifier with Simple Calcula⁃tion［J］. IEEE Transactions on Power Electronics，2013，28 （7）：3428-3437.

［9］Lu T M，Zhao Z B，He F，et al. Compensation of Control Delay and Discrete Control Error in Predictive Direct Power Control for Three-level PWM Rectifier［J］. International Symposium on Power Electronics for Distributed Generation Systems，2010，24（1）：829-834.

［10］Bouafia A，Gaubert J，Krim F. Design and Implementation of Predictive Current Control of Three-phase PWM Rectifier Using Space-vector Modulation（SVM）［J］. Energy Conver⁃sion & Management，2010，51（12）：2473-2481.

修改稿日期：2015-11-20

Research on Modified Predictive Direct Power Control of PWM Rectifier

ZHENG Hong1，2，WANG Zheyu2，HUANG Jun2，ZHANG Yun2
（1. Key Laboratory of Facility Agriculture Measurement and Control Technology and Equipment of Machinery Industry，Zhenjiang 212013，Jiangsu，China；2. College of Electrical and Information Engineering，Jiangsu University，Zhenjiang 212013，Jiangsu，China）

Abstract:Introduced predictive direct power control（PDPC）theory and principle to select voltage vector. Active power and reactive variable quantities of traditional PDPC are controlled by the same cost function. So when one variable quantity subject disturbance，the other variable quantities will subject disturbance too，that cause mutual interference and result dynamic performance of PWM decrease. Proposed a novel PDPC which introduce weighting factors of active power and reactive power to reset cost function，which can minimize interference and improve dynamic and stability. Simulation of Matlab/Simulink result and experiment result based on prototype shows，compared with conventional PDPC，proposed method can improve dynamic and stability performance of PWM rectifier.

Key words:PWM rectifier；direct power control（DPC）；predictive control；cost function

收稿日期：2015-05-15

作者简介：郑宏（1965-），男，博士，教授，Email：zhenghong0511@sina.com

基金项目：江苏高校优势学科建设工程资助项目（61074019）

中图分类号：TM46

文献标识码：A