一种高精度线阵ccd二维自准直仪四狭缝目标中心的定位方法

董彦维，贾军强，万 琦，刘希强，段祉鸿

（1. 北京航天发射技术研究所，北京，100076；2. 中国航天科工集团公司二院二部，北京，100084）

一种高精度线阵ccd二维自准直仪四狭缝目标中心的定位方法

董彦维1，贾军强2，万 琦1，刘希强1，段祉鸿1

（1. 北京航天发射技术研究所，北京，100076；2. 中国航天科工集团公司二院二部，北京，100084）

为满足高精度线阵ccd二维自准直仪动态高精度测量，提出一种高精度线阵ccd二维自准直仪四狭缝目标中心的定位方法，首先采用高斯滤波对ccd图像进行平滑处理，在抑制噪声的同时生成带有高斯加权的ccd图像，然后采用线性插值质心法对加权图像进行目标中心亚像素定位。实验结果表明，该定位方法稳定性好，定位精度高且实时性强，在原理样机上，应用该方法实现了单次二维角度测量时间小于0.2 s，测量范围±900″，在±300″内相对于进口eLcOMaT3000示值误差优于±0.5″，具备工程应用价值。

高精度线阵ccd；二维自准直仪；高斯滤波；线性插值质心法；亚像素定位

0 引 言

光电自准直仪作为一种高精度瞄准及小角度测量仪器，在航天发射地面瞄准和定位等方面有着不可替代的作用[1]。光电自准直仪具有较高的测量精度和稳定性[2]，ccd自准直仪是其典型代表。高精度线阵ccd二维自准直仪是以高精度线阵ccd作为光电传感器实现二维小角度的动态高精度测量。常用的亚像素定位方法有质心定位法[3]和线性插值质心法[4]等，但都有自己的局限性：只能处理特定目标中心图像，并且存在易受噪声干扰和运算量大等问题。因此，高精度线阵ccd二维自准直仪的研制，需要寻找一种快速高精度线阵ccd二维自准直仪四狭缝目标中心定位方法。线阵ccd成像系统中的量化噪声近似服从高斯分布[5]，采用高斯滤波能很好地抑制图像噪声。为了实现二维小角度快速高精度测量，本文提出一种高精度线阵ccd二维自准直仪四狭缝目标中心的定位方法。首先采用高斯滤波对ccd图像进行平滑处理，在抑制噪声的同时生成带有高斯加权的ccd图像，然后采用线性插值质心法对加权图像进行目标中心亚像素定位。

1 自准直仪测量原理

自准直仪以自准直原理为基础[6]，用测微系统对被测件进行角位移精密测定，其原理如图1所示。

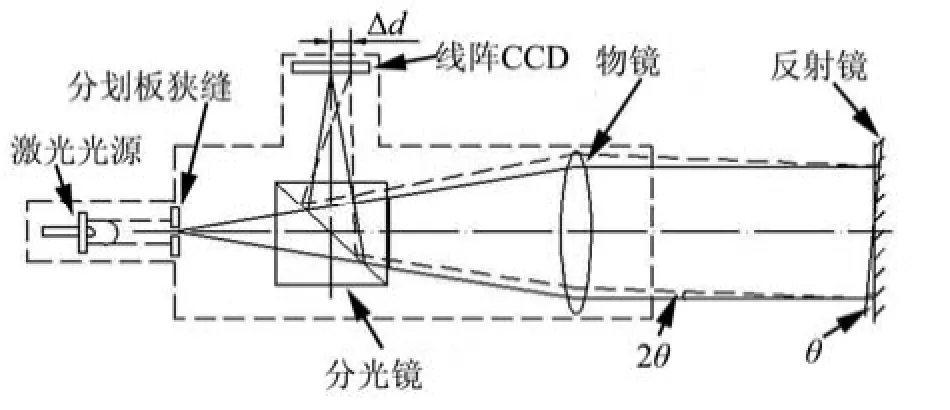
图1 自准直仪测量原理

当激光光源发送光束照亮位于物镜焦平面上的分划板狭缝，通过分光镜和准直物镜后形成一束平行光射向被测反射镜，当反射镜面垂直于光轴时，光束仍然原路返回，由准直物镜汇聚，经分光镜成像于线阵ccd上；当被测反射镜发生小角度变化时，分划板狭缝在线阵ccd上所成的像将产生线位移，由此可以计算相应的小角度变化。反射镜发生小角度变化θ，则在线阵ccd上成像产生位移Δd，根据几何光学原理，有：Δd=f·tan2θ，其中，f为物镜焦距。当被测角θ很小，约小于15′时，测量公式近似为Δd=f/2θ，则：

由式（1）可知，只要能精确测量线阵ccd的像位移Δd，即可精确测量小角度θ。为了实现测量反射镜的二维角度变化，需要增加1束激光光源、1块分光棱镜和1片线阵ccd。通过控制光源切换和信号采集，实现二维角度测量。

2 四狭缝目标中心亚像素定位方法

目前最常用的中心定位亚像素算法是质心法，其算法简单且定位精度较高，但是它只能处理目标面积区域适中的图像，并且受噪声干扰较大，当图像信噪比较小时，它的定位误差会变大[7]。线阵ccd成像过程中的随机噪声近似服从高斯分布。高斯滤波对服从高斯分布的噪声有很好的滤波效果，同时还能保留图像细节。因此，为了降低噪声对算法精度的影响，提高系统精度，首先采用高斯滤波进行预处理，生成带有高斯加权的ccd图像，然后采用线性插值高斯加权质心算法对高斯加权的ccd目标图像中心进行亚像素定位。

2.1 高斯滤波预处理算法[8]

图像滤波是通过原始输入图像f( x, y)与脉冲响应h( x, y)的卷积来实现，即：

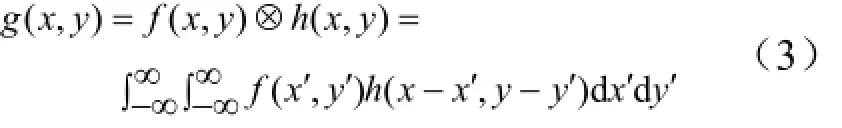
式中 ⊗为卷积运算符；(,)g x y为经过滤波后的输出图像。式（3）的离散形式为

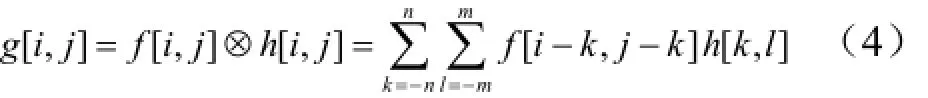
因此，卷积变成对像素点的加权计算，脉冲响应[,]h i j是一个卷积模板，21m+和21n+是卷积模板的二维宽度。对图像中的每一个像素[,]i j，输出响应[,]g i j通过平移卷积模板到每个像素点[,]i j处，计算模板与像素点[,]i j邻域加权得到。其中各加权值对应卷积模板的各对应值。

高斯卷积模板是一种线性模板，可直接从二维零均值离散高斯函数计算模板权值[9]。二维零均值离散高斯函数表达式为

式中 σ为高斯函数的均方差，控制平滑效果。σ值越大，平滑程度越好，但同时也造成图像特征过分模糊（图像细节的丢失），一般选取σ=1～10。例如，取σ=1，为了减少实际运算量，卷积模板的二维宽度取3×3，图2为式（5）产生的高斯卷积模板示意。

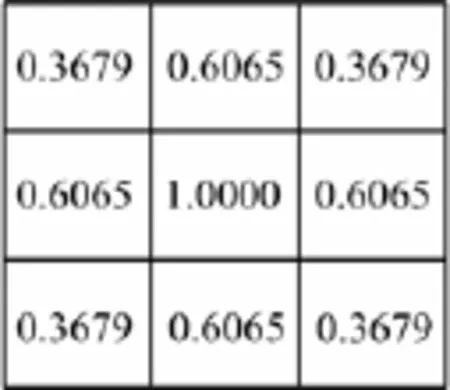
图2 3×3二维高斯卷积模板

为方便计算，一般将模板权值取整。其过程是取模板最小权值（在模板的角点处），选择系数k使得最小权值为1。如式（5）中：

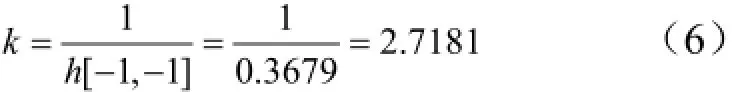
对k取整为3。这样，用k值乘以模板所有权值，并取整得到图3所示的整数值高斯卷积模板。

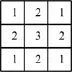
图3 3×3整数值二维高斯卷积模板

图3中高斯卷积模板的权值之和不等于1，意味着高斯卷积处理提高了整幅图像的灰度，并改变了图像直方图。所以，在进行图像平滑处理时，像素点的输出值必须用模板的权值归一化处理。在式（5）中：

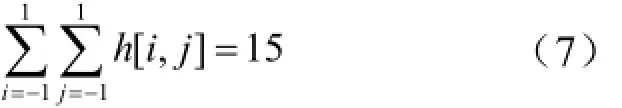
所以，经高斯卷积平滑滤波后的输出图像为

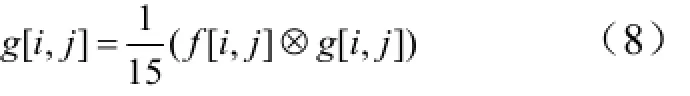
二维高斯模板的数学表达式为

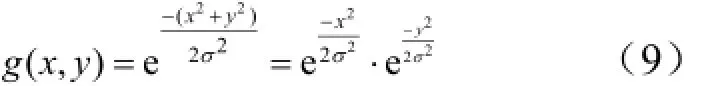
式（9）可以分解成两个一维的高斯函数，对应一个二维高斯模板，可以将其分解成2个一维高斯模板的卷积，如图4所示。

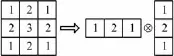
图4 高斯模板分解示意

在高精度线阵ccd二维自准直仪原理样机上实际采用的是一维高斯模板，如图5所示。

图5 实际应用的1×3高斯模板

实验中，一个线阵ccd采集到的四狭缝目标图像减去固定阈值后的图像如图6所示。从图6可以看出，由于系统噪声的影响使图像的边缘不平滑。采用图5所示的一维高斯模板平滑滤波后的图像如图7所示。从图7可以看出，经过高斯平滑滤波后的图像边缘非常平滑，对系统噪声起到了很好的抑制作用。采用1×3高斯模板，运算量小，实时性强。

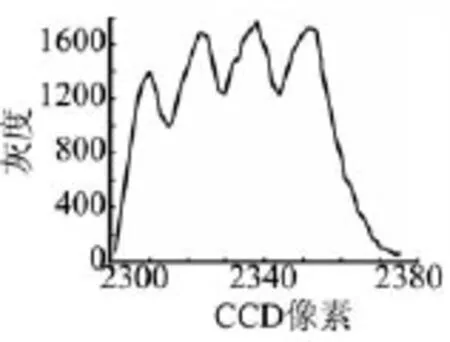
图6 原始ccd图像

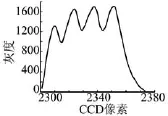
图7 经过高斯平滑滤波后的ccd图像

2.2 线性插值高斯加权质心算法

利用1×3高斯模板可以快速有效抑制高精度线阵ccd图像的噪声，同时保留图像细节。为了进一步提高二维自准直仪的定位精度，兼顾定位算法的实时性，本文采用线性插值高斯加权质心算法对四狭缝目标中心进行快速亚像素定位。

为了减少数据处理量、提高处理速度，对四狭缝目标图像减去固定阈值后的ccd图像进行中心定位，用传统质心算法求目标中心为[10]

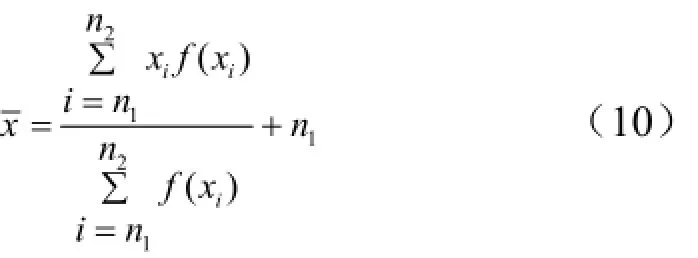
在质心定位过程中，噪声对定位精度有较大影响，因此采用高斯加权的质心定位具有较高的去噪声能力[8]。在质心定位中不采用原图像像素灰度值而是采用高斯滤波后的灰度值进行计算。故由式（10）得到的高斯加权质心算法为

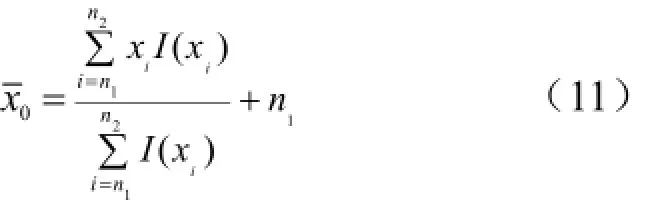
其中，

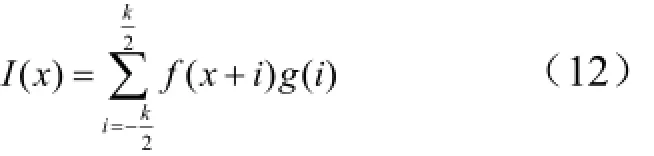
目标中心的定位精度与目标图像灰度的轮廓和信噪比有很大关系，因此，可以通过插值的方法在目标成像区域增加一些可利用的点，提高质心定位精度。由于Lagrange多项式得到的线性插值最为简单，实用性强，对噪声的抑制、图像质量的提高效果较好[10]。因此，本文选用Lagrange线性插值。根据线性插值理论，设点xi，xi+1的带高斯加权的灰度值分别为I( xi)，I( xi+1)，插值点为v，则：

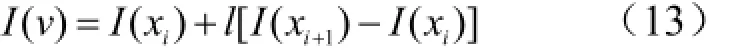
其中，

经过插值运算后，目标图像的中心可由下式计算：

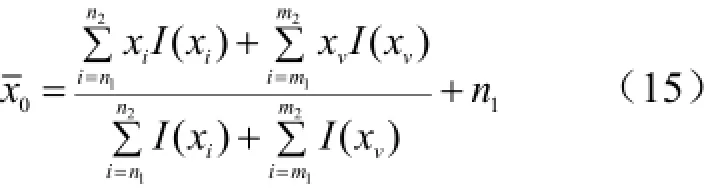
3 结果及数据分析

采用本文提出的定位方法，已在高精度线阵ccd二维自准直仪原理样机上成功实现了快速精确亚像素定位。为了验证该定位方法的精度和速度，选用德国穆勒公司的eLcOMaT 3000型自准直仪进行对比。在±300″范围内，x轴和y轴测量的对比结果与误差分别见图8和图9。

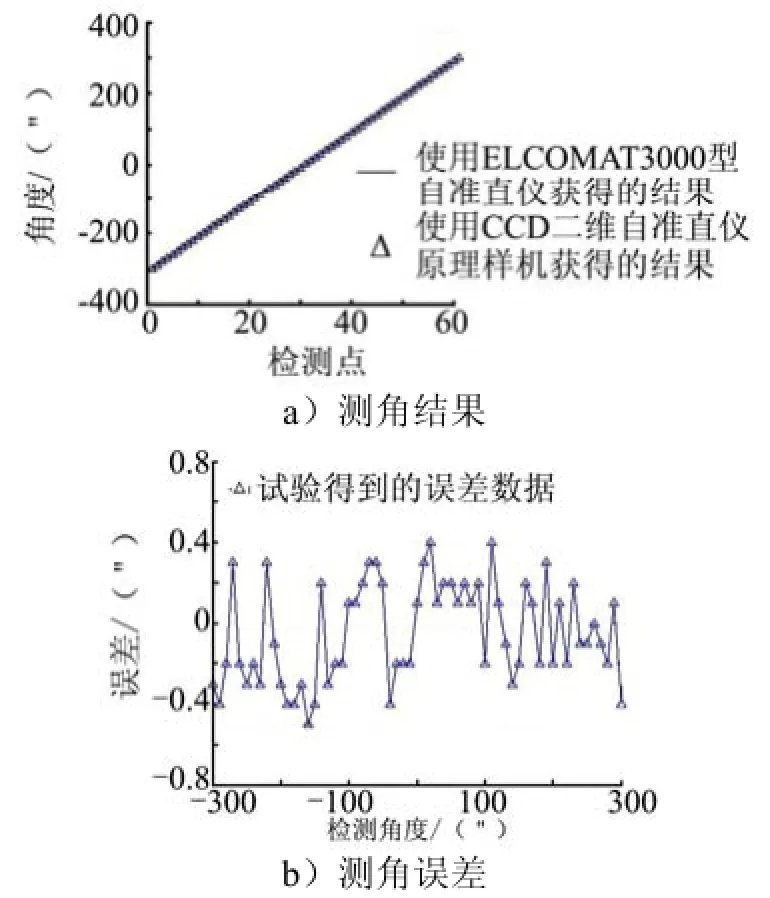
图8 x轴测角结果与测角误差

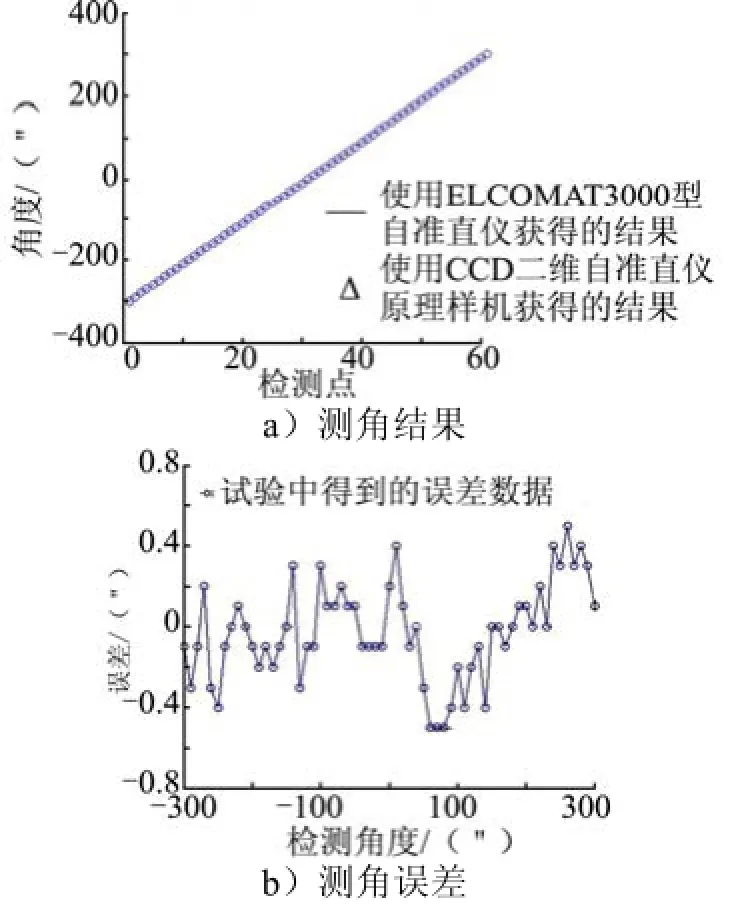
图9 y轴测角结果与测角误差

eLcOMaT 3000在全量程（±1 000″）范围内示值误差不超过0.25″，在任意20″内示值误差不超过0.10″。比较结果非常接近，测得原理样机X轴和Y轴测量范围±900″，在±300″内相对于进口eLcOMaT 3000示值误差优于±0.5″，单次二维角度测量时间小于0.2 s，实现了快速高精度二维角度测量。

4 结 论

本文提出一种基于高精度线阵ccd二维自准直仪四狭缝目标中心的亚像素定位方法，首先采用高斯滤波对ccd图像进行平滑处理，在抑制噪声的同时生成带有高斯加权的ccd图像，然后采用线性插值质心法对加权图像进行目标中心亚像素定位。在原理样机上，应用该方法实现了单次二维角度测量时间小于0.2 s，测量范围±900″，在±300″内相对于进口eLcOMaT3000示值误差优于±0.5″。实验结果表明，该定位方法稳定性好，定位精度高且实时性强，具备工程应用价值。

[1] 敖磊, 谭久彬, 崔继文, 等. 一种快速高精度激光ccd自准直仪圆目标中心的定位方法[J]. 光学学报, 2007, 27(2): 253-254.

[2] 张明丽, 刘立人, 万玲玉,等. ccd扫描检测光束准直度[J]. 光学学报, 2005, 25(8): 1067-1071.

[3] Jie Y, Long X. ccd-area-based autocollimator for precision small-angle measurement[J]. Review of Scientific Instruments, 2003, 74(3): 1362-1365.

[4] 贺俊吉, 张广军. 结构光三维视觉检测中光条图像处理方法研究[J]. 北京航空航天大学学报, 2003, 29(7): 593-597.

[5] 丁晓华，李由，于起峰，等. ccd噪声标定及其在边缘定位中的应用[J].光学学报, 2008, 28(1): 99-104.

[6] 欧同庚, 陈志高, 杨博雄, 等. ccd光电自准仪工作原理及误差源分析[J]. 大地测量与地球动力学, 2007, 27(S1): 98-100.

[7] 刘兆蓉, 王志乾, 刘绍锦, 等. 激光光斑中心精确定位算法研究[J]. 计算机仿真, 2011, 28(5): 399-400.

[8] 张广军. 视觉测量[M]. 北京: 科学出版社, 2008.

[9] Kohl T R. Vision tutor lab guide[M]. Massachusetts: amerinex artificial Intelligence, 1992.

[10] 尚学军, 何明一, 王军良. 基于线阵ccd的光斑定位算法研究[J]. 激光与红外, 2008, 38(7): 730-731.

A High-accuracy Location Method for 4-Reticle Target Center of Linear Array CCd 2-axis Autocollimator

dong Yan-wei1, Jia Jun-qiang2, Wan Qi1, Liu Xi-qiang1, duan Zhi-hong1
(1. Beijing Institute of Space Launch Technology, Beijing, 100076; 2. The Second department of the Second academy, china aerospace Science & Industry corporation, Beijing, 100084)

To realize the dynamic high-accuracy measurement of high-accuracy linear array ccd 2-axis autocollimator, a high-accuracy location method for 4-reticle target center of high-accuracy linear array ccd autocollimator is proposed. First, ccd images are processed with Gauss-filter, which diminishes the noise and generates weighted images. Then, the sub-pixel location of weighted image’s target center is acquired accurately by using barycentre method based on linear polynomial interpolation.experimental results show that the proposed method is stable and accurate. appling the method on the prototype, as a result, the measuring time of a single 2-axis angle measurement is less than 0.2s. The measure scope is ±900″. The proposed method can efficiently fulfill the requirements in engineering systems.

High-accuracy linear array ccd; 2-axis autocollimators; Gauss-filter; Barycenter method based on linear polynomial interpolation; Sub-pixel location.

V556

a

1004-7182(2016)01-0081-04

10.7654/j.issn.1004-7182.20160119

2014-08-11；

2015-04-23

董彦维（1979-），男，工程师，主要从事定位定向、光电瞄准和图像处理研究