某焦化厂供水网络多目标建模及优化

韩庚，曹萃文，顾幸生（华东理工大学化工过程先进控制与优化技术教育部重点实验室，上海 200237）



某焦化厂供水网络多目标建模及优化

韩庚，曹萃文，顾幸生
（华东理工大学化工过程先进控制与优化技术教育部重点实验室，上海 200237）

摘要：对某焦化厂的供水网络进行了详细的分析，在用水供需平衡满足生产要求的前提下，以新鲜水供给量最小以及新鲜水供给成本与循环水及除盐水的浪费成本之和最小作为两个优化目标，建立了多目标混合整数非线性规划（MINLP）的数学模型。利用文献提出的Pareto规则下的多目标改进文化差分进化算法对模型进行了求解。所得的计算结果与现场实时操作数据相比，模型及算法实现的优化操作减少了新鲜水消耗量，降低了新鲜水供给成本与循环水及除盐水的浪费成本，达到了很好的优化效果。

关键词：焦化厂；供水网络；混合整数非线性规划；多目标改进文化差分；多目标优化

第一作者：韩庚（1990—），男，硕士研究生。联系人：曹萃文，副教授，硕士生导师。E-mail caocuiwen@ecust.edu.cn。

在焦化厂生产运行中，当前对供水网络的研究主要集中在如何构造新鲜水量最小的供水网络，却忽视了该水网络的不唯一性，因此对水系统集成优化方案的分析和决策需要考虑新鲜水用量、用水系统的成分和用水网络结构的复杂程度等方面。在实际生产中，供水网络优化设计方案的确定一般需要在这三者之间进行折中和协调，属于多目标优化问题。利用水系统集成技术对焦化厂供水网络进行优化设计与改善，同时利用采集的现场数据对模型进行验证和改进，可以使水处理系统的配置更加科学合理，提高水资源的综合利用效率。目前国内外对于流程工业企业公用工程供水网络系统的研究，针对供水网络的最优设计和运行优化主要形成了3种方法：夹点分析法、数学规划法以及夹点分析与数学规划混合法。

在20世纪70年代末，夹点分析法作为一项技术被开发应用于实时热回收。从那时起，夹点分析法基于流程整合的原则已演变成最优化的一般方法。夹点分析法不仅已成功地应用于能源系统，而且在节约新鲜水、实现废水最小化、生产能力去瓶颈等方面亦得到了广泛应用[1-2]。水夹点分析作为最佳的水网络的设计工具，一直在最小利用水资源领域存在显著进步。文献[3-5]展示了水夹点分析法在公用工程水网络系统方面的应用。英国曼彻斯特理工大学的SMITH教授等[6]于1994年领导进行了水系统集成的研究，并发表了著名的论文“wastewater minimization”（废水最小化）。在这篇论文中，许多水网络优化研究中的重要概念被首次提出来，包括极限水曲线、极限水复合曲线、水夹点分析法等。SMITH教授参照过程热集成中构造冷热复合曲线的方法，构造出了极限水复合曲线。其工作洞察了整个水系统，指出哪里是用水的制约瓶颈、最小新鲜水用量及最小污水产生量的目标值以及如何考虑系统中污水的再生利用。2000年SAVELSKI和BAGAJEWICZ[7-8]利用水夹点技术在论文中阐述了在过程工厂中单组分水利用网络的最优必要条件。这些必要条件对应在考虑单一污染物的基础上污水回用的最佳水量分配规划问题，其目标是使总取水口的水量最小化。对于多杂质水网络的研究。2003年，SAVELSKI和BAGAJEWICZ[9]提出了精炼厂和过程工厂中最优的多组分水分配系统的必要条件，其为被文献[7]证明的单杂质单污染物最优必要条件的延伸。特别的是，它表明在新鲜水使用者过程的出口至少有一个部件能够到达最大浓度。

将数学规划法应用于实际过程工厂水网络优化配置中的首要工作是建立与实际工程相符合的数学规划模型，其模型根据实际的约束、原料、成分、杂质等因素又可分为LP（linear programming）、NLP （nonlinear programming）、MILP（mixed integer linear programming）和MINLP（mixed integer nonlinear programming）模型，并且模型中包括不同的目标函数和约束条件。数学规划出现于20世纪40年代末，是由美国哈佛大学的DORFMAN等[10]最先使用的。1980年TAKAMA等[11-12]在一座石油炼油厂具有所有可能性的再利用和再生机会的超结构基础上，提出了一种优化水资源配置的方法。2004年，KIM和SMITH[13]提出了一种新的考虑到时间上限制的不连续供水系统的设计方法，并且该网络设计在最低的成本下可以被系统识别，由此产生的优化问题可以通过一个MINLP模型解决。该设计方法在功能上可以适应设计的复杂性和实际中遇到的具体问题，因为其可以提供一个可靠、稳健的起点。2006年，袁希钢等[14]针对工业用水网络中那些单组分质量负荷不确定的情况，提出了修正的对称模糊规划模型，同时提出了以新鲜水用量最小化，总连接流股数最小和总流率最小为目标函数的多目标混合整数对称模糊规划模型以及求解算法。2008年，曹雨平等[15]建立了针对石油化工企业的用于多水源用水网络优化的单目标LP模型，该模型主要用于解决含多个水质不同的供水水源的用水网络优化设计问题，将新鲜水量折算为成本后加上排污费用的和为其目标。相比水夹点分析技术，数学规划法具有更高的灵活性，求解速度快，并且可以更加全面地考虑水网络优化设计中的各种约束条件，因此，自从1980年TAKAMA等[11-12]在一座石油炼油厂应用数学规划法构建了水资源优化配置网络后，其在工业生产中应用范围越来越广。利用数学规划法优化配置水网络对模型建立的要求非常高，因为其模型的准确度决定了与实际生产过程的相似度，因此目标函数和约束条件越接近实际情况越好。

水夹点分析基于对过程用水的理解，给出了用水网络设计的基本规则，在此基础上建立过程使用新鲜水、排放废水和回用的各种可能匹配方案的用水网络超结构及其MINLP模型，剔除一些不合理的结构。MINLP模型因一些整数变量和连续变量等于零而维数降低，既避免了用水夹点综合设计用水网络得不到真正意义上的最优解，又在一定程度上防止了超结构规模过大，但MINLP维数太高，求解困难。对于利用数学规划方法进行超结构分型建模、水夹点分析和研究，已经有很多人为此展开了研究[16-17]。姚平经等[18]提出了水夹点分析和数学规划法相结合的用水网络最优设计法，建立了过程使用新鲜水、排放废水和回用的各种可能匹配方案的用水网络超结构及其MINLP模型，并采用通用代数建模系统GAMS得到用水网络最优设计方案。2007年，HUL等[19]将粒子群算法进行修改，用于求解水网合成系统的MINLP模型。

在焦化厂供水网络系统的建模和优化中，由于现实模型中变量个数多、模型规模大以及非线性强的特点，用智能算法进行求解逐渐成为了一种新趋势。利用智能优化算法研究现实中数学模型得到了很好的效果，并且还有很大的研究潜力。本文基于在某焦化厂调研得到的真实数据，在文献[15]和文献[20]工作的基础上，对某焦化厂的供水网络进行了详细的分析，加入了表示除盐水和循环水装置浪费状态的二元变量，建立了该焦化厂供水网络的多目标MINLP模型。并用多目标改进文化差分算法[20-21]对模型进行了求解。计算结果表明：在满足生产中水量的需求条件下，按优化结果进行的操作能够降低新鲜水供给，减少循环水和除盐水的浪费，降低成本，提高经济效益。

1　某焦化厂供水网络现状分析

1.1某焦化厂供水网络结构

该焦化厂的公用工程供水网络系统由工业水系统、循环水系统、除盐水系统3个部分构成，其负责为焦化厂的各个生产装置设备及连接的分厂区供应所需的标准水源。其中，整个厂区的供水网络结构图包含焦化厂供水系统A和焦化厂供水系统B两部分，具体如图1和图2所示。

该焦化厂工业给水岗位由一水厂、二水厂、生活水3部分组成。其中，工业给水岗位的任务是为各生产分厂、车间、部门及有关的外厂提供合格的生产用水及生活用水，主要保证生产过程达到供水稳定、安全、经济运行，为生产装置安全连续运行提供可靠的基本生产条件。主要包括工业水1、工业水23kt滤池，还包括滤液回收、130t锅炉以及一些工业水的用户等部分。

工业水系统中，一路新鲜的源水通过江中取水头部，经虹吸式潜江管至取水泵房集水井，经过旋转滤网，拦截源水中的杂物，用离心泵抽水，送至低压江水管道，浑水在流经低压管道时用加注泵投加适量的混凝剂混合，经过管式静态反应器送至机械搅拌澄清池。从沉淀池和澄清池出来的水流入清水库，作为一水厂区水处理源水，流入清水库，再送3000t水池作为新碳一运行中心水处理原水，其流程如图1所示。另一路新鲜的源水用离心泵抽水进入综合池，作为二水厂水处理源水，供老碳一运行中心水处理原水，其流程如图2所示。

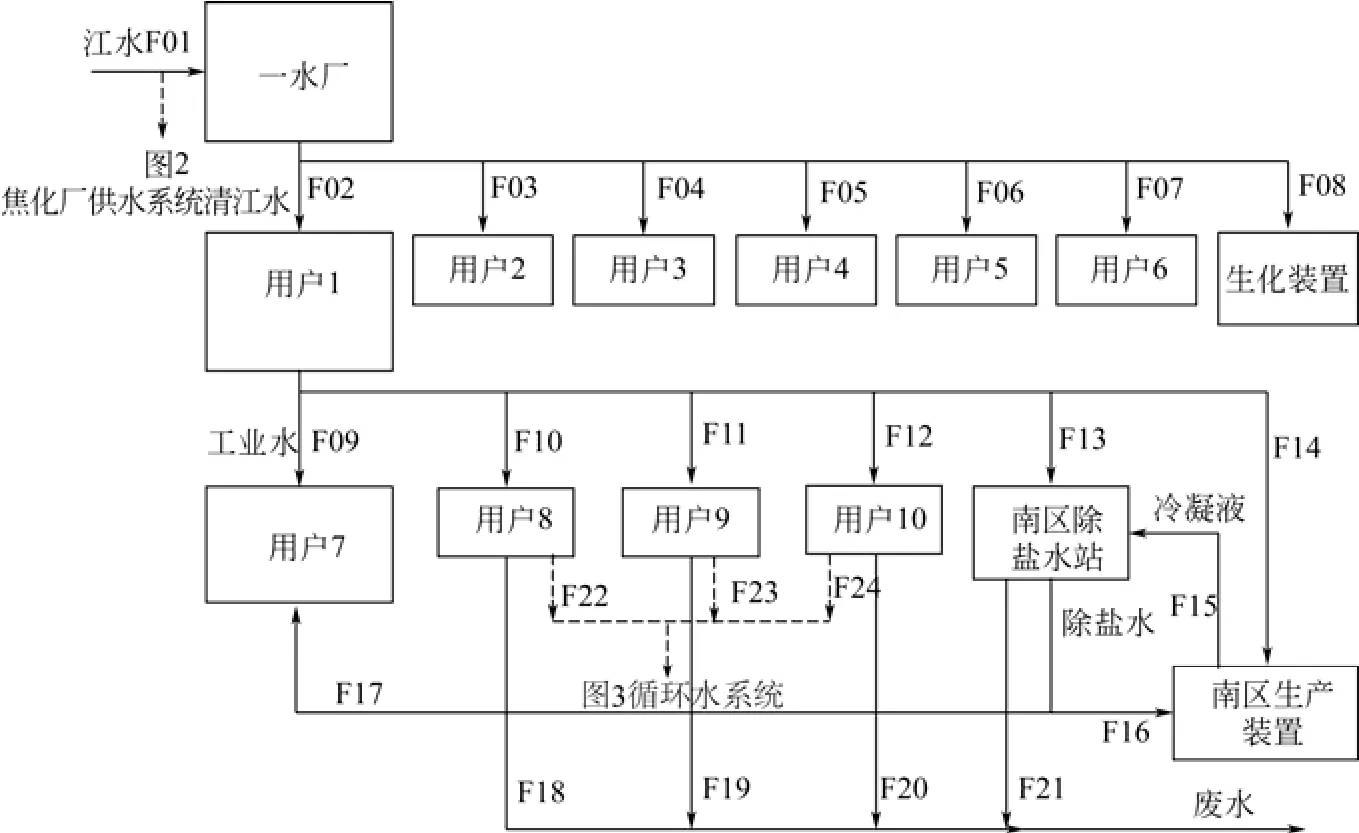
图1　焦化厂供水系统A

图2　焦化厂供水系统B

循环水系统包括6套循环水装置，分别为：用户15循环水装置0.40～0.60MPa，用户16循环水装置0.50～1.0MPa，用户17循环水装置0.30～0.80MPa，用户9循环水装置0.40～0.60MPa，用户10循环水装置0.40～0.60MPa，用户8循环水装置0.40～0.60MPa。具体如图3所示。

除盐水系统在全厂有南北两个除盐水站，其中南区除盐水负责生产电导率≤0.2μS/cm、SiO2≤20μg/L的二级除盐水，供南区生产装置使用，包括除盐水用户8～用户13，要求安全连续、保质、保量供水。北区除盐水站负责生产电导率≤5μS/cm、SiO2＜0.1mg/L的一级除盐水和电导率≤0.2μS/cm、SiO2＜20μg/L的二级除盐水，供北区生产装置使用，一级除盐水主要供给除盐水用户1～用户5，二级除盐水主要供给除盐水用户6和除盐水用户7使用。具体如图4所示。

在生产过程中，生化装置负责用户11、南区生产装置以及北区生产装置产生的部分废水，其余废水经过环保处理直接排沟。

1.2供水网络存在的问题及研究目标

经过对该焦化厂公用工程水网络系统的详细调研，对数据进行分析，发现目前该焦化公司水系统的损失主要由以下4方面组成。

图3　循环水系统

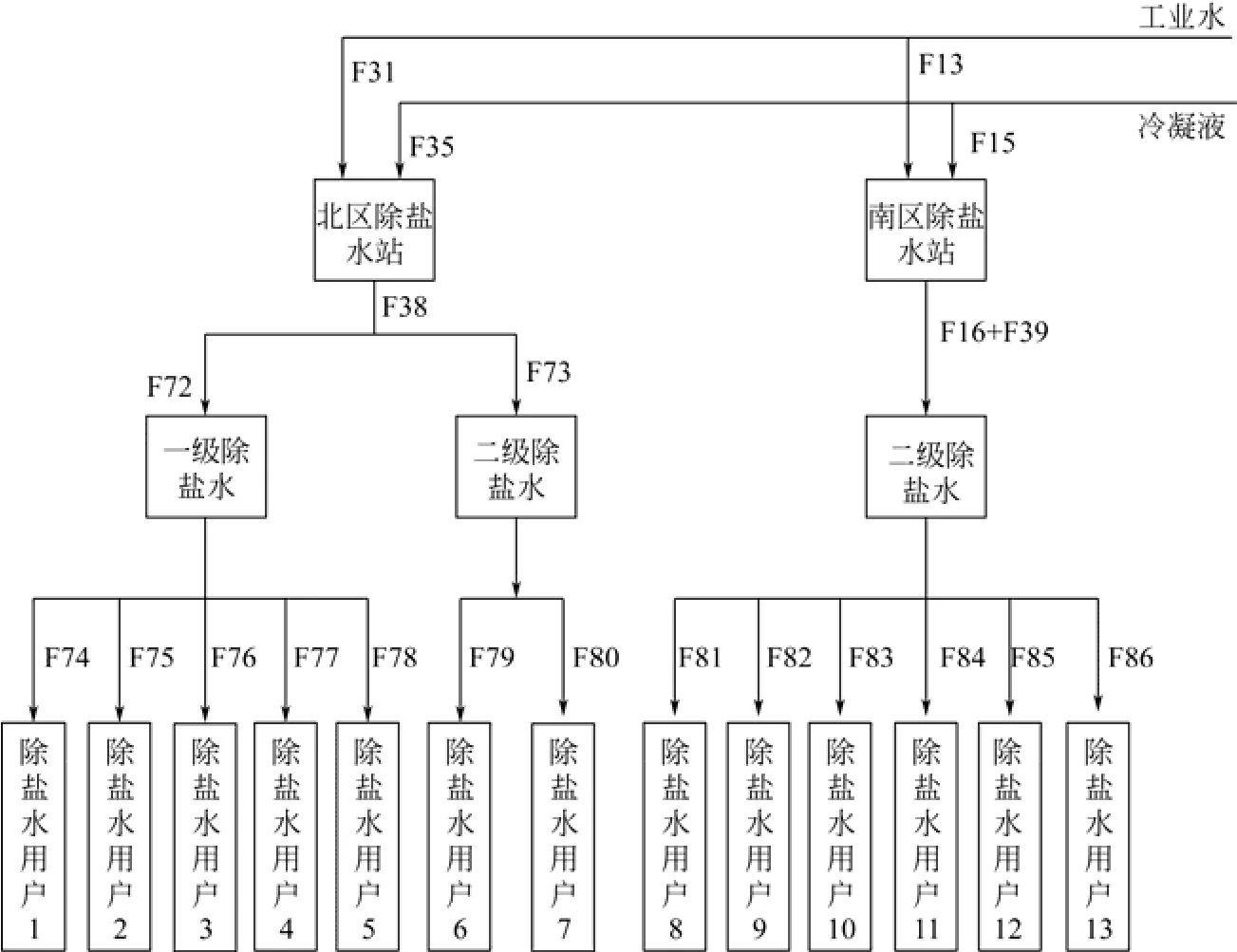
图4　除盐水系统

（1）清江水损失 焦化公司的工业水、清江水损失主要来自于自身的自清洗、反洗、吹泥工序，损失量占自身用量的4％左右。

（2）除盐水损失 焦化公司的除盐水损失主要来自于再生而产生的污水外排，损失量占自身用量的20％左右。

（3）循环水损失 焦化公司的循环水损失主要来自于自身的蒸发损失与排污损失，蒸发量占总系统循环水总量的0.2％～0.5％，排污量占蒸发量的50％左右。

（4）水系统的其他损失 焦化公司的水系统的其他损失主要来自于自身的管路损失。

基于所得调研资料，建立完整的供水网络平衡系统，以新鲜水供给量最小和新鲜水供给成本与循环水及除盐水的浪费成本之和最小作为目标，建立双目标的供水系统数学模型，求出满足生产需求的最小水源供给量与最小经济成本，减少损失现象，增加系统中水源利用率。

2　供水网络的数学模型

该焦化厂供水网络建模的对象包含该厂的工业水系统、除盐水系统、循环水系统三部分。本文以满足各个用户需求为约束建立供水网络系统的多目标MINLP模型，所有单元设备的处理能力和各流股流量用连续变量表示，用0-1变量表示在给定操作条件下对应的循环水和除盐水设备是否存在水源浪费。模型的目标函数包括两个目标，分别是新鲜水消耗量最少以及新鲜水供给成本与循环水及除盐水的浪费成本之和最小。

2.1某焦化厂供水网络的双目标MINLP模型

在已有数据的基础上，分析该焦化厂的供水用水设备及线路，对该焦化厂的供水网络进行建模，建立了供水网络系统的MINLP模型。

2.1.1某焦化厂公用工程水网络配置及参数

通过对调研数据的分析和整理，该焦化厂共有工业水系统、除盐水系统、循环水系统3个部分的局部或全局管网，包括南区生产装置、北区生产装置以及循环水使用、除盐水使用等用水单元以及管损和排沟的水流损失。

表1、表2、表3分别为该厂工业水系统、循环水系统、除盐水系统供耗水装置及其参数属性。在供水调度的过程中，首先要考虑的是流量指标约束满足供需平衡。

2.1.2某焦化厂双目标MINLP模型的建立

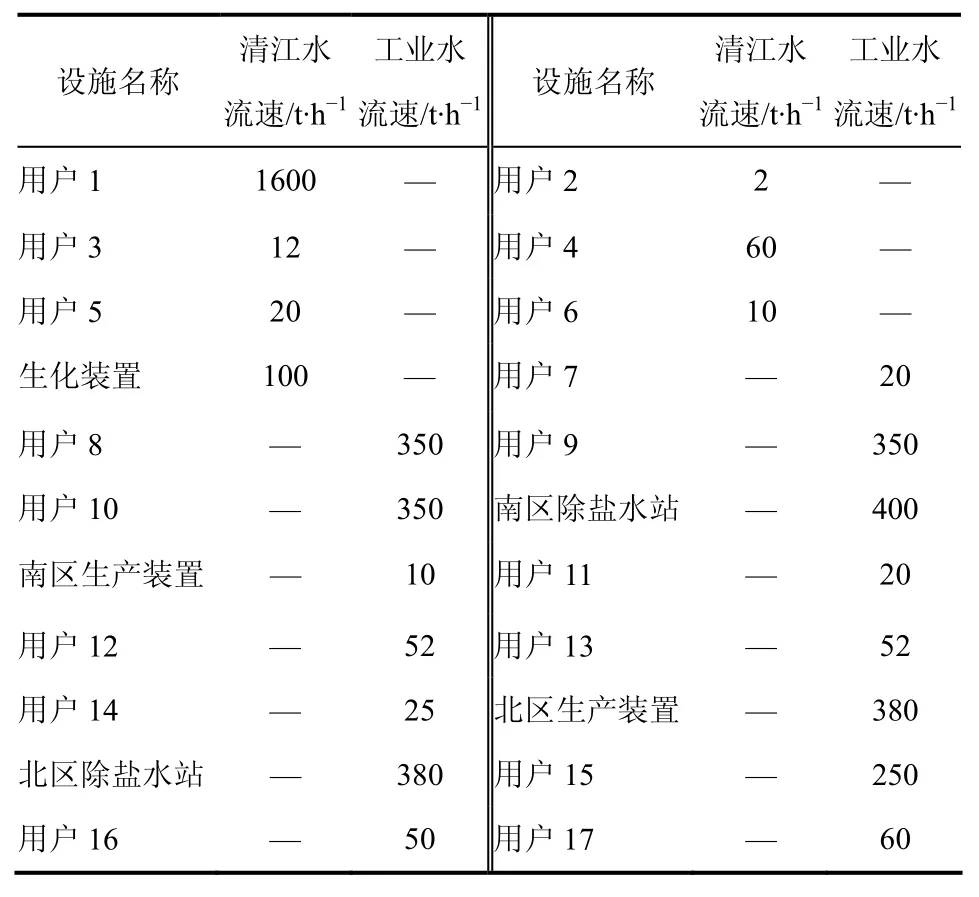
表1　工业水系统供耗水装置及其参数属性

表2　循环水系统供耗水装置及其参数属性

模型的目标函数一是新鲜水供给量最少，也就是向一水厂和二水厂提供的新鲜水的水量和最小；模型的目标函数二是新鲜水供给成本与循环水及除盐水的浪费成本之和最小，如式(1)所示。

对各供水、用水装置流量进行编号，形成的模型的约束如式(2)。

式(2)表示某公用工程水网络系统管网中，总水源应大于等于总消耗水量。Fi'表示已经除去管损的供水流量值，见式(3)。

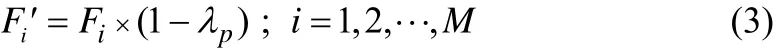
式(3)是计算除去管损管道中水流流量的经验公式，其中lp是水源p管道中管损的经验值，不同的生产环境条件下，管损的经验值不同，如式(4)、式(5)。

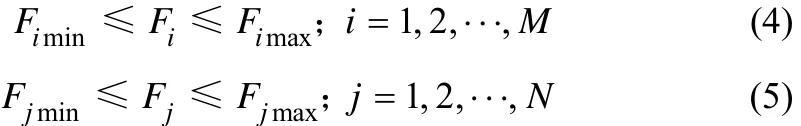
式(4)和式(5)表示管道中供水流量和用水单元的值都应该在设计的范围之内。

在这些消耗水源的装置单元中，基本都是常开单元，而一些循环水及除盐水装置的水源浪费是可优化项，用二元变量来表示这些装置是否有水源浪费，如式(6)。

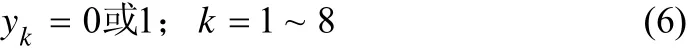
则加入二元变量的耗水装置的实际水源浪费量为式(7)。

针对该厂的实际公用工程供水网络的系统结构根据（图1～图4），对流量按图上所示的编号，可以得到该水网络的多目标MINLP模型如式(8)～式(33)。

目标函数

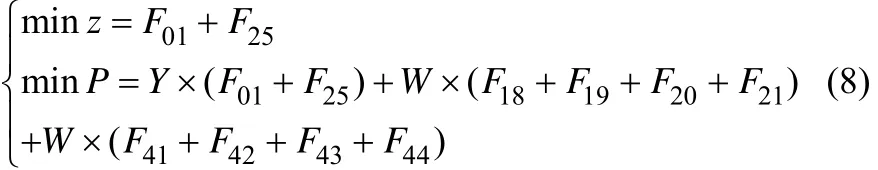
约束条件

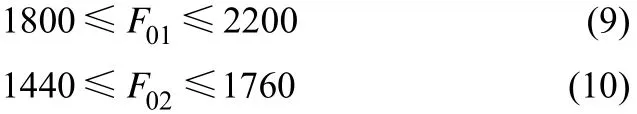
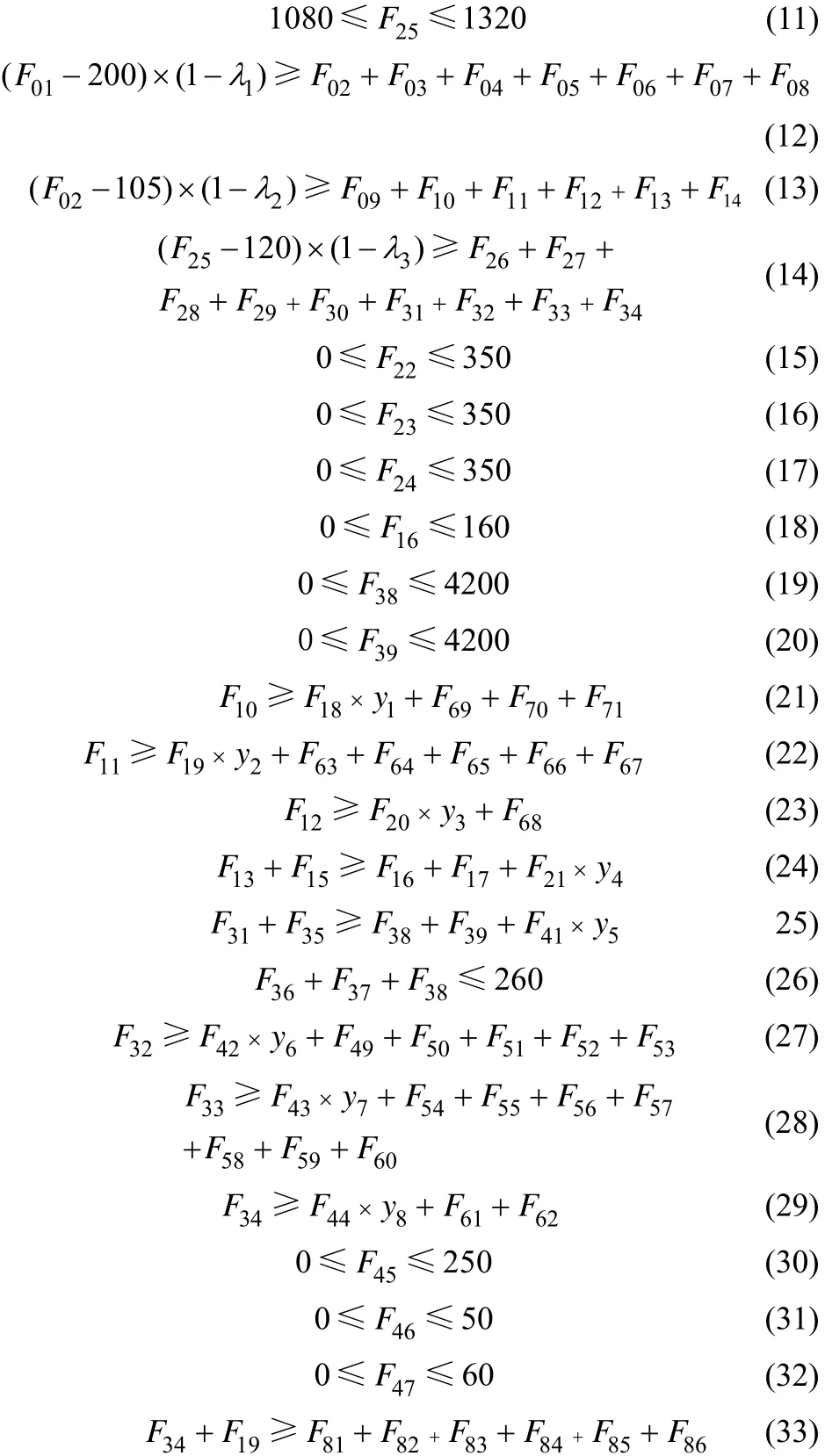
以上这些公式描述了该焦化厂供水网络系统不同水源不同水型之间的供求关系、管道损耗和装置流速的设计范围约束。该模型共有94个决策变量，其中86个表示不同设备不同水源流速的连续变量、8个判断循环水和除盐水设备是否存在水源浪费的整数变量、25个不等式约束方程。

公式中的流速和焦化厂中各用水装置的流速一一对应，列出如下。

（1）图1

（2）图2

（3）图3

（4）图4

2.2基于多目标改进文化差分算法的MINLP模型的求解

根据现场采集的生产状况数据，本文选取夏季稳定工况一段时间内的平均数值作为该厂各生产设备消耗的稳定数据。模型的变量主要有各装置耗水量、可优化的设备流量等。对模型中实际存在循环水和除盐水浪费的装置设定为0-1整数变量，建立该焦化厂供水网络的多目标MINLP模型，采用文献[21]中的多目标改进文化差分算法进行求解。

该算法运行环境为Win7系统，CPU频率为2.5GHz的，酷睿i5处理器，8G内存，优化运行一次时间为10min。用于求解模型的多目标改进文化差分算法的参数设置为：种群规模NP为100，最大进化代数gen_max为10，总运行次数TOTAL为50，交叉因子F为0.5，交叉概率CR为0.158。

以目标一（新鲜供给量最小）作为X轴，目标二（新鲜水供给成本与循环水及除盐水的浪费成本之和最小）作为Y轴，双目标归一化后的Pareto前沿如图所5示，反归一化后的Pareto前沿如图所6示。由于最小化两个优化目标为目的，所以先取归一化后的Pareto前沿上距离原点最近的4个点为选取的（如图6所示）优化结果，再对应到反归一化后的实际目标的Pareto前沿（如图所5示）中的对应位置取得优化操作结果，最后与采集的现场数据进行对比，可以得到如表4所得结果。由于本文MINLP模型包含94个变量，无法一一列出，所以在表中只列出其主要变量，包括2个新鲜水源水量流速、6个循环水装置的循环水水量流速、南区除盐水站和北区除盐水站的除盐水水量流速以及循环水与除盐水水源浪费的整形变量。

图5　归一化后的Pareto前沿

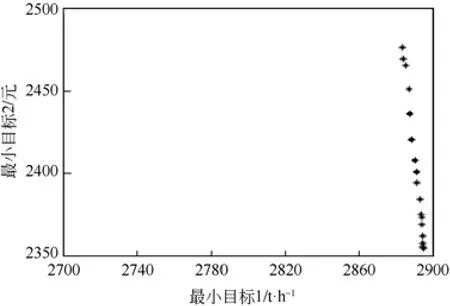
图6　双目标Pareto前沿

将取得的最优解与采集的焦化厂现场实时操作数据比较，根据表4列出的4组比较数据可以看出，现场数据新鲜水总消耗量为3451.51t/h，4组改进文化差分算法的计算结果分别为2880.94t/h，2887.94t/h、2880.87t/h、2885.97t/h，分别比现场实时数据减少了570.57t/h、563.57t/h、570.64t/h、565.54t/h的消耗量，在节约水资源方面具有很好的效果；同时，实际工况中原有循环水和除盐水水源浪费的8个装置优化后均没有水源浪费，所有的水都被充分利用，循环水及除盐水的浪费成本为0，同时达到了新鲜水消耗最少和新鲜水成本与排放废水装置的循环水及除盐水的浪费成本最小的目的。这也说明建立的多目标MINLP模型和用于求解的改进文化差分算法具有很好的优化效果。

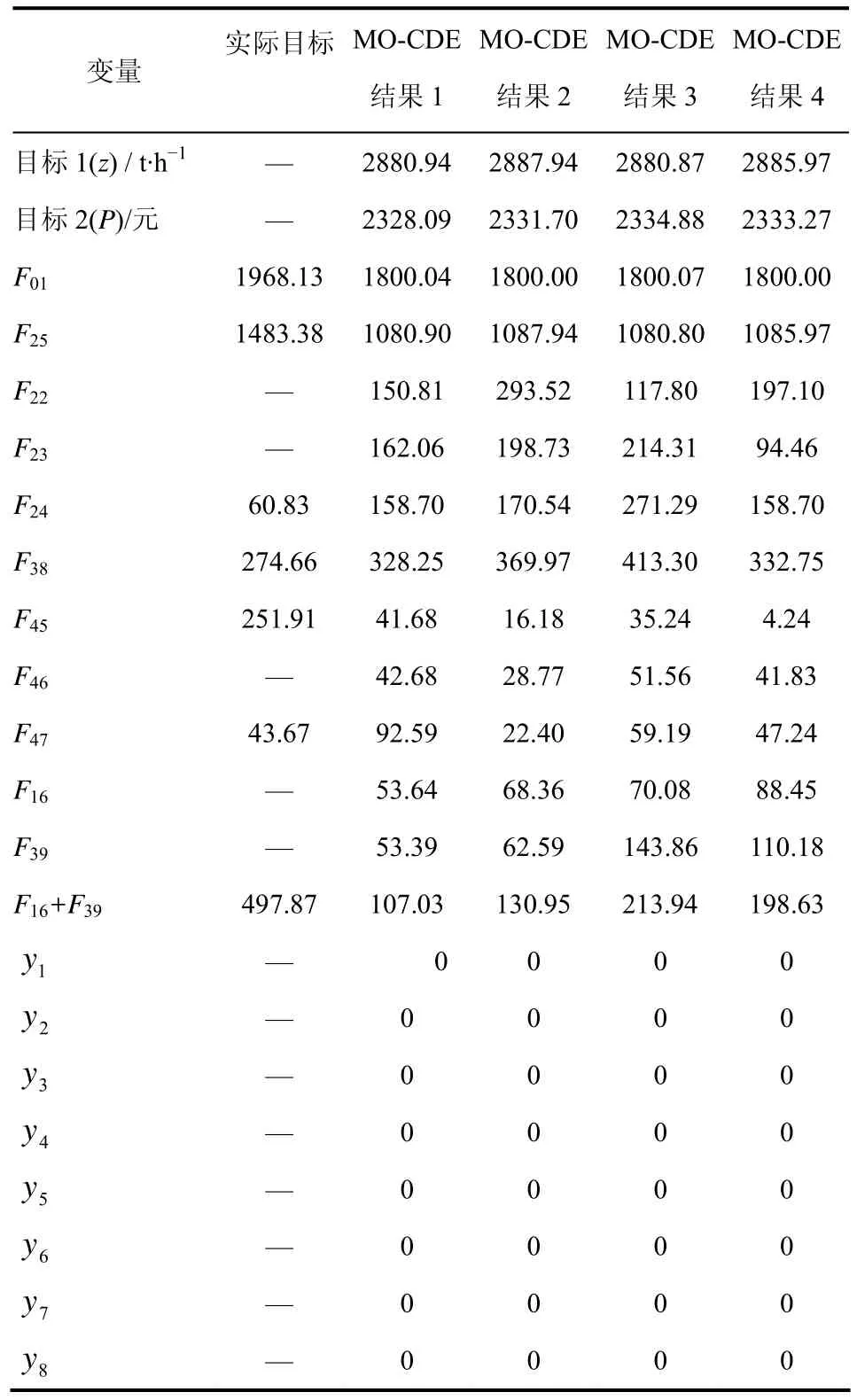
表4　双目标MINLP模型的变量和结果

应该说明的是，上述结论是在某焦化厂实际生产的一个稳态工况下得出的，如果生产状况发生改变（例如某装置对不同水源的消耗量有变动等），需要进一步考虑生产状态不确定产生的影响，这也是将来的研究工作。

3　结论

本文对某焦化厂的供水网络进行了详细的分析，在用水供需平衡满足生产要求的前提下，建立了多目标MINLP（混合整数非线性规划）的数学模型。利用文献[20]提出的Pareto规则下的多目标改进文化差分算法对模型进行了求解，通过计算结果与现场实时操作数据的对比可以看出，建立的多目标MINLP模型和用于求解的改进文化差分算法减少了该焦化厂供水网络新鲜水水源的消耗量，同时降低了新鲜水供给成本与循环水及除盐水的浪费成本，达到了预期的优化效果。

在今后的工作中，对于焦化厂供水网络这个结构，可以进行更深入的分析，如建立该系统在不确定环境下优化决策的模型，实现不确定环境下该系统的优化等。

符 号 说 明

参考文献

[1]SMITH R. Chemical process design[M]. New York：McGrawHill，1995：2011-2013.

[2]LINNHOFF B. User guide on process integration for the efficient use of energy[M]. Houston，TX：Gulf Publishing Co.，1994.

[3]LINNHOFF B. Use pinch analysis to knock down capital costs and emissions[J]. Chemical Engineering Program，1994，90（8）：32-57.

[4]ROSSITER A P. Waste minimization through process design[M]. New York：McGraw Hill，1995.

[5]EL-HALWAGI M M. Pollution prevention through process integration[J]. Clean Products and Processes，1998，1：5-19.

[6]WANG Y P，SMITH R. Wastewater minimisation[J]. Chemical Engineering Science，1994，49（7）：981-1006.

[7]SAVELSKI Mariano，BAGAJEWICZ Miguel. Design of water utilization systems in process plants with a single contaminant[J]. Waste Management，2000，20：659-664.

[8]SAVELSKI M J，BAGAJEWICZ M J. On the optimality conditions of water utilization systems in process plants with single contaminants[J]. Chemical Engineering Science，2000，55：5035-5048.

[9]SAVELSKI M J，BAGAJEWICZ M J. On the necessary conditions of optimality of water utilization systems in process plants with multiple contaminants[J]. Chemical Engineering Science，2003，58：5349-5362.

[10]DORFMAN R，SAMUELSO P A，SOLOW R M. Linear programming and economic analysis[M]. New York：Dover Publications Inc.，1987.

[11]TAKAMA N，KURIYAMA T，SHIROKO K. Optimal water allocation in a petroleum refinery[J].Computers Chemical Engineering，1980，4（4）：251-258.

[12]TAKAMA N，KURIYAMA T，SHIROKO K. On the formulation of optimal water allocation problem by linear programming[J]. Computers & Chemical Engineering，1981，5（2）：119-121.

[13]KIM J K，SMITH R. Automated design of discontinuous water systems[J]. Transactions of the Institution of Chemical Engineers. Part B，Process Safety and Environmental Protection，2004，82（3） ：238-248.

[14]刘永健，袁希钢，罗祎青. 基于模糊规划的质量负荷不确定水网络的综合[J]. 化工学报，2006，57（4）：867-872.

[15]曹雨平，杨瑞洪，姜如荣. 多水源用水网络优化模型研究[J]. 化工环保，2008，28（4）：327-332.

[16]STEFANO Alvisi. Multiobjective optimization of rehabilitation and leakage detection scheduling in water distribution systems[J]. Journal of Water Resources Planning and Management，2009，135（6）：442-450.

[17]FESTA G，VERDE D，MAGINI R. Rehabilitation of a water distribution system with diffused water losses[C]//International Conference on Sustainable Water Resources Management，5th，2008：426-439.

[18]李英，姚平经. 水夹点分析与数学规划法相结合的用水网络优化设计[J]. 化工学报，2004，55（2）：220-225.

[19]HUL S，TAN R R，AURESENIA J. Water network synthesis using mutation-enhanced particle swarm optimization[J]. Transactions of the Institution of Chemical Engineers. Part B，Process Safety and Environmental Protection，2007，85（b6）：507-514.

[20]李晓楠. 基于改进文化差分算法的蒸汽网络建模与优化[D]. 上海：华东理工大学，2015.

[21]李晓楠，曹萃文，顾幸生. 一个真实化工厂蒸汽网络系统的建模与优化[J]. 计算机与应用化学，2015，32（3）：266-270.

Multi-objective modeling and optimization for the water supply network of a coking plant

HAN Geng，CAO Cuiwen，GU Xingsheng
（Key Laboratory of Advanced Control and Optimization for Chemical Process，Ministry of Education，East China University of Science and Technology，Shanghai 200237，China）

Abstract：In this paper，the water supply network system of a real-world cooking plant was deeply analyzed. Under the balance between water supply and demand，a bi-objective mixed-integer nonlinear programming（MINLP） model was built. Minimizing the fresh water supply and the total cost of fresh water，recycle water and desalting water were the two objectives. The Pareto based multi-objective cultural differential evolution（MO-CDE） algorithm of reference was selected to solve this model. The computing results showed that the bi-objective optimal results were better than current operational parameters in reducing the fresh water supply and the cost of fresh water，recycle water and desalting water.

Key words：coking plant；water-supply network；mixed-integer nonlinear programming（MINLP）；multi-objective cultured differential evolution（MO-CDE）；multi-objective optimization

中图分类号：TP 29

文献标志码：A

文章编号：1000–6613（2016）04–1033–09

DOI：10.16085/j.issn.1000-6613.2016.04.011

收稿日期：2015-10-16；修改稿日期：2015-11-05。

基金项目：国家自然科学基金（61174040，61573144）及上海市自然科学基金（12ZR1408100）项目。