Research on the Fracture Toughness for Ship Cracked Plates Based on the Accumulative Increment Plastic Deformation

,,,

(1a.Key Laboratory of High Performance Ship Technology,Ministry of Education;b.School of Transportation,Wuhan University of Technology,Wuhan 430063,China;2.Depts of Naval Architecture,Ocean and Structural Engineering,School of Mechanical and Ship Engineering, Qinzhou University,Qinzhou 535000,China)

Research on the Fracture Toughness for Ship Cracked Plates Based on the Accumulative Increment Plastic Deformation

DENG Jun-lin1a,b,2,DU Bo2,YANG Ping1a,b,CHEN Yuan1a

(1a.Key Laboratory of High Performance Ship Technology,Ministry of Education;b.School of Transportation,Wuhan University of Technology,Wuhan 430063,China;2.Depts of Naval Architecture,Ocean and Structural Engineering,School of Mechanical and Ship Engineering, Qinzhou University,Qinzhou 535000,China)

The crack tip opening displacement(CTOD)is an important parameter to evaluate material fracture toughness and analyze the crack propagation due to low-cycle fatigue damage.An analytical model is presented to determine CTOD for the Ship cracked plates subjected to low-cyclic axial in-plane loadings.Combined with Dugdale’s model,the accumulation plastic deformation at the crack tips is used as controlling parameter to estimate cyclic CTOD for low-cycle failure analysis of the ship central-through cracked plates.The second order polynomial for the normalized CTOD defined as a function of the accumulative plastic strain,the ratio of mean stress to the yield stress, and the crack length is fitted by the least square method.The new accumulative plastic strain based on CTOD estimation presented in this paper provides a new way for low-cycle fatigue analysis,considering accumulative plastic damage for central-through cracked plates under high cyclic loadings.

low-cycle fatigue;central-through cracked plate;accumulative plastic strain; CTOD

0 Introduction

The fatigue strength of ship’s structure has a very important significance on the safety and survivability.Along with the increasing in ship dimensions and more use of high-strength steel in recent years,the stress and deformation of ship structures are so high and large,which result in a very prominent problem of low-cycle-fatigue(LCF)damage to large-scale ships. This has become the key issue demanding prompt solution in the development of large-scale ships.For cracked plates of ship and marine structures,plastic strain would generate in the region near crack tip when the local stress reaches the yield strength.When a ship is subjected to cyclic loads in waves,plastic strain would accumulate in local region of the crack tip,andthis accumulative incremental plastic strain would speed up the fracture failure of the structure when it accumulates to a certain degree along with the increasing of the cyclic loading number.Crack tip opening displacement(CTOD)and J integration are the major parameters to describe crack propagation of ductile structural materials[1].However,J integration is rarely used to assess the structure fracture under cyclic loads because it cannot apply to unloading state.Therefore,studying and establishing assessment methods of CTOD based on accumulated plastic strain under cyclic loading have great practical significance.

CTOD reflects the plastic deformation performance in the region near crack tip;its value reflects the resistance of material fracture toughness at crack tip.It is a measurement of plastic deformation at crack tip,so it is widely used as a criterion of the fracture failure.Previously,CTOD calculation models based on stress intensity factor K had been proposed for applying only to linear elastic state[2-3].Dugdale[2]model has been widely studied and used for establishing the corresponding relationship between external loads and crack parameters.Jiang[4]analyzed CTOD of ship stiffened plate based on Dugdale model and found out the influence rule caused by external load,stiffness ratio and other factors.Finite element method[5-8]is one of the efficient ways in studying elastic-plastic fracture problems,thus it is widely used in various kinds of fracture assessments.It is used to study CTOD and other relative parameters through calculation of crack-tip stress-field and displacement-field.Potirniche[5]calculated the size of crack-tip plastic zone and CTOD of the steady microscopic structural small crack, and high-precision CTOD is obtained through bringing two-dimensional small strain constitution relation of the single crystal plasticity theory into finite element software ANSYS.Wu et al[6]proposed an effective method to estimate fracture toughness of the test specimen based on the numerical results of CTOD.In their studies,elastic-plastic finite element method is used to calculate the CTOD,taking tensile specimen with axial notch as the research object.Chen[7-8]has carried out numerical analysis of CTOD based on the crack maximum opening displacement(CMOD),and simplified the finite element calculation model by eliminating the effects of external load,model dimensions,material properties,and crack length.Besides,some researchers have studied CTOD based on the local strain of the crack tip,and proposed the CTOD calculation model which can only be applied to low strain and static loading[9-11].Shimanuki[12]proposed a new method to assess local stress based on the relationship between local stress and linear elastic fracture mechanics.He discussed corresponding relationship between local strain and CTOD,and realized the idea to determine CTOD based on local strain by two-dimensional finite element method.There are a lot of discussions about using these calculation models for cracked structures under complex load.At present,many researchers have studied CTOD under complex loads,and obtained their corresponding conclusions.Alike putting forward CTOD calculation models[13-14],Østby[15]calculated large plastic strain of cracked pipeline structure,and proposed a simple CTOD evaluation method based on the plastic strain.Zhang[16]discussed the CTOD evaluation model for marine pipeline structure under large plastic strain, considering the influence of crack size,material hardening exponent and external loads.

Among the above mentioned analyses,the studies on CTOD are either confined to linear elastic state or only about finite element analysis of plastic strain under static load.There is few fracture assessment about cracked plate under LCF load.Taking central-through cracked plate as the study object,the paper establishes a CTOD calculation model based on accumulative plastic strain at crack tip,under low cycle and high stress external load.The influence of mean stress and crack length are analyzed.The analysis provides a feasible way for fracture failure assessment for ship and marine structural component under actual cyclic loading.

1 Theoretical analysis

1.1 The relationship between CTOD and accumulative increment plastic strain at crack tip

For elastic-perfectly plastic material,the infinite central-through cracked plate under uniform tension load was studied and the approximate calculation formula about CTOD was obtained by Dugdale[2]as:

where σsis the material yield stress,a¯is equivalent crack length,σ is applied load.

In the determined plane state,for infinite central-through cracked plate under cyclic loading,the corresponding function between Δσ of CTOD and cyclic stress Δσ can be expressed as:

Assume stress and strain of material meet the hardening rule of Ramberg-Osgood under cyclic loadings:

In cyclic strain situation,the plastic strain is the main part while the elastic strain is relatively small,so elastic strain can be ignored.The relationship between plastic strain and cyclic stress can be expressed as:

According to Eq.2 and Eq.4,the relationship between Δδ of CTOD and increment of accumulative increment plastic strain Δεpcan be shown as follows:

where Δδ is the variation of CTOD,Δεpis the accumulative increment plastic strain.

As long as the expression of Eq.5 is ascertained and accumulative increment plastic strain obtained,Δδ of CTOD value of infinite plate with central-through crack under cyclic loading can be easily estimated.This is a new method proposed to assess the elastic-plastic performance of infinite plate with central-through crack under cyclic loading.

1.2 Accumulative increment plastic strain of crack tip under cyclic loads

The equation between plastic strain and accumulative plastic strain in Chaboche model can be differentiated as[17]:

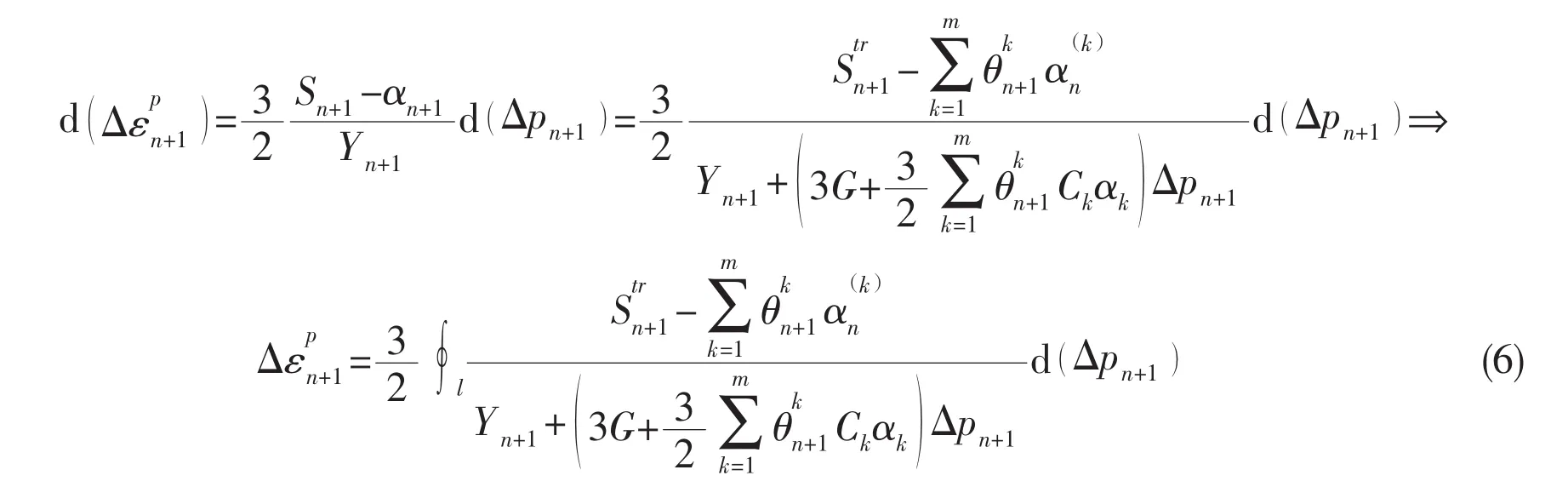
where Δpn+1is the equivalent plastic strain increment in the n+1 cycle,which can be obtained by Newton-Raphson iteration;αkand Ckare material constants which describe material hardening properties;S,α are the partial stress tensor and back stress tensor respectively;and Yn+1are the functions of the unknown variable Δpn+1.

So the accumulative plastic strain increment Δεn+1after n+1 cycles can be calculated. Plastic strain increment in each cycle can also be derived by updating the corresponding parameters.The relationship between plastic stress and strain of the central cracked plate at crack tip in n+1 cycle can be expressed as[18-19]:

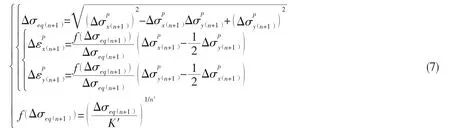
Substituting Eq.7 into Newton-Raphson iteration formula[17],thus plastic strain increment Δpn+1after n+1 cycles can be calculated,and accumulative plastic strain increment Δεn+1after n+1 cycles can be obtained by Eq.6.The relationship between accumulative plastic strain increment after n+1 cycles and plastic strain increment in n+1 cycle can be expressed as:

According to Eqs.6～9,the accumulative plastic strain after n+1 cycles can be written as:

Therefore,Eq.9 is the expression for the value of the accumulative increment plastic strain around crack tip of central-through cracked plate after n+1 cycles.

2 Finite element analysis and discussion

In order to calculate and analyze conveniently,and to improve the data processing efficiency,APDL language of ANSYS software is used to conduct the parametric modeling and finite element analysis.Plane182 of ANSYS is adopted as the element type and material constitutive relation model is chosen according to Chaboche nonlinear reinforcement principle.Fig.1 shows a central-through cracked infinite plate and the finite element mesh model.Here 2L is the plate length,2W is the plate width,2a is the crack length.Let a=10 mm,L=150 mm,and W=130 mm in simulating the infinite central-through cracked plate.Singular element is used to deal with crack tip,and refined mesh is adopted in crack tip region.Steel 304 is selected in the finite element model,and Tab.1 shows the material parameters.

Tab.1 Material parameters of stainless steel 304

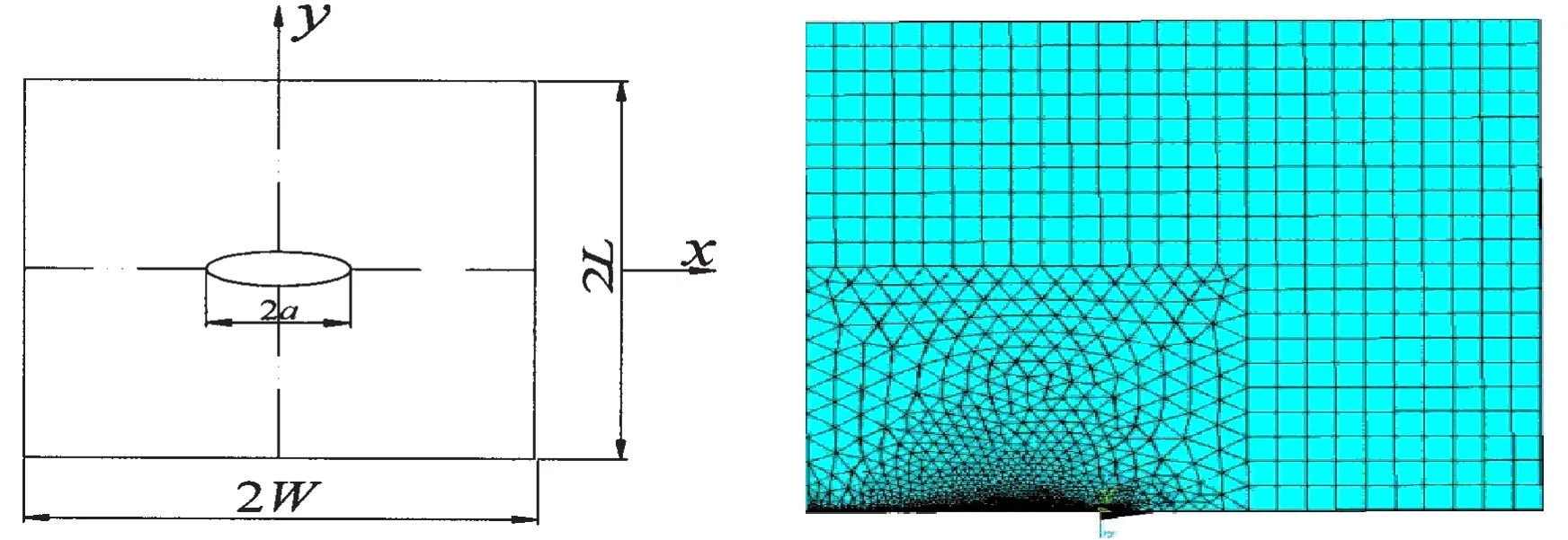
Fig.1 The plate with central-through crack and a quarter FE model

2.1 Curve of stress vs.strain at crack tip under cycle loadings

Through numerical analysis by FEA,based on Chacoche model,the hysteresis loops between stress and strain of the crack tip along with the crack propagation under cycle loadings are shown in Fig.2.It shows the hysteresis loops at three different locations.As shown in Fig.2,crack propagates gradually and plastic deformation accumulates obviously in local crack tip field,with the increasing of the cycle loading number.

2.2 Relation about accumulative plastic strain and cyclic times

Fig.2 The stress-strain curve at the crack tip of Chaboche cyclic plastic model

According to the calculation of the fi-nite element model in Fig.1,the influence of mean stress σmand stress amplitude σaon the accumulative plastic strain at crack tip is investigated through changing only one of them respectively.Let the crack length a=10 mm and other parameters remain unchanged.The relation curves about accumulative plastic strain and cyclic times under different mean stress σmand stress amplitude σaare shown in Figs.3～4 from the results of a series finite element calculation.

Fig.3 The curve of accumulative plastic strains vs. cyclic number under different mean stress σm

Figs.3～4 show that the accumulative plastic strain increases and stabilizes gradually as the cyclic times increasing when the mean stress σmincreases.It reveals that the mean stress and stress amplitude affect accumulative plastic deformation a lot under cyclic loadings.

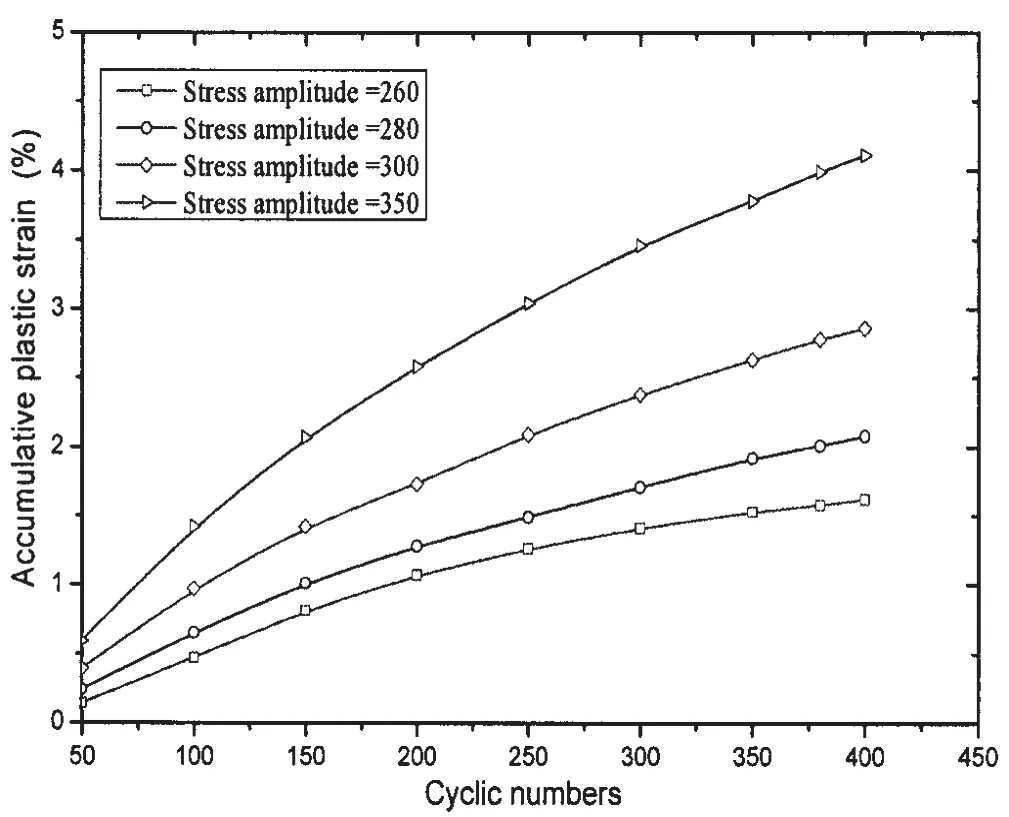
Fig.4 The curve of accumulative plastic strains vs.cyclic number under different stress amplitudes σa

According to the model of Fig.1, when investigating the influence of mean stress σmand stress amplitude σaon CTOD,the model with a=10 mm,L=150 mm and W=130 mm are adopted,and the material parameters are those in Tab.1. In the calculation,elastic-perfectly plastic material and von Mises yield criterion are adopted.In addition,for a certain of mean stress(σm=180 MPa or 240 MPa), let the stress amplitude σabe the values of 20 MPa,30 MPa,to 170 MPa respectively.The elastic-plastic finite element method is carried out to calculate the changeable CTOD of the central-through cracked plate under cyclic loadings,and the results are shown in Fig.5.

Fig.5 The curve of the CTOD vs.stress amplitude under different mean stress σm

The results in Fig.5 show that for constant crack length,the CTOD increas-es as the stress amplitude σaincreasing when the mean stress σmkeeps unchanged.Moreover, CTOD increases as the mean stress σmincreasing at the same stress amplitude σa.

From the results shown in Figs.3～5,it is shown that mean stress and stress amplitude affect obviously CTOD and accumulative plastic strain under cyclic loadings.Therefore,they should be taken into consideration when assessing the fracture toughness of central-through cracked plate under cyclic loadings.

3 Functional relationship between CTOD and accumulative increment plastic strain at crack tips

Because the results from stress method are not so good,the strain method has been widely used to assess fracture behavior of the marine tubular structures under large plastic deformation[20].In this paper,a CTOD calculation equation based on accumulative increment plastic strain is presented to assess the fracture failure behavior of infinite plate with central-through crack under cyclic loading.

For the model shown in Fig.1,Δεpand CTOD of the central-through cracked plate under given cyclic loadings have been calculated,and then the functional relation between CTOD and Δεpcan be achieved by results fitting based on the least square method.The functional relation can be expressed as:

where Δεpis accumulative plastic strain of the crack tip,a is crack length,W is width of cracked plate.

The paper adopts second order polynomial function to express Eq.10.The undetermined coefficients in the function Eq.10 will change with mean stress,stress amplitude and crack length,which can be calculated by fitting calculation results based on least square method. Therefore,the influence of mean stress, stress amplitude and crack length on fitted function should be investigated to ensure the fitting function meet the actual needs.

3.1 The effect of mean stress

When investigating the influence of mean stress σm/σson the functional relationship between CTOD and Δεp,we adopt unchanged stress amplitude(σa=50 MPa)but different mean stress(σm=180 MPa,200 MPa,240 MPa).The CTOD and Δεpcan be calculated with the same material parameters of Tab.1,and the results after standardized treatment are shown in Fig.6.

Fig.6 The curve of the CTOD value vs.accumulative plastic strain under different σm/σa

Fig.6 shows that CTOD gradually increases with accumulative incremental plastic strain under constant mean stress.Moreover,when stress amplitude is unchanged and mean stress increases,CTOD will increase with increasing of accumulative plastic strain at crack tip.

From the results as shown in Fig.6,based on the least squares method,the undetermined coefficients of the functional relation between CTOD and Δεpare fitted,which eventually determine the CTOD equation for assessing central-through cracked plate based on accumulated plastic strain at crack tip.The fitted CTOD equation is as:

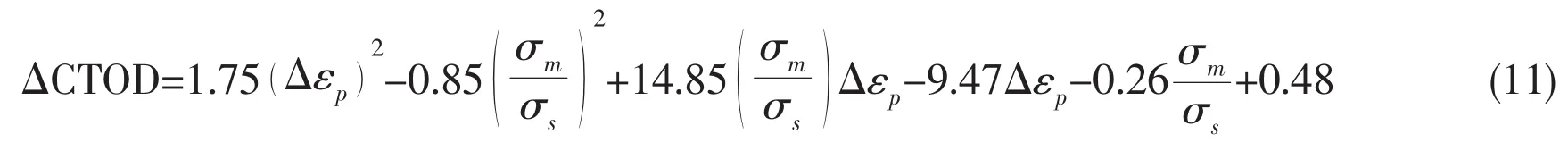
3.2 The effect of crack length

When investigating the influence of crack length on the functional relationship between CTOD and Δεp,we adopt unchanged mean stress(σm=200 MPa)and stress amplitude(σa=150 MPa)but different crack length(a=10～20 mm).Let L=150 mm and W=130 mm for the finite element model of Fig.1.CTOD and accumulative increment plastic strain Δεpat crack tip can be calculated through a series of finite element models of central-through cracked plate,with the same material parameters of Tab.1,and the results after standardized treatment are shown in Fig.7.

Fig.7 The curve of the CTOD value vs.accumulative plastic strain under different a/W

Fig.7 shows that CTOD gradually increases with accumulative incremental plastic strain at crack tip under constant mean stress and stress amplitude.Moreover,when stress amplitude is unchanged and mean stress increases,CTOD increases with the increasing of accumulative plastic strain.It reveals that when external loading is determined,the changing of crack length obviously affect CTOD.When crack propagation happens on the central-through cracked plate under cyclic loadings,the structural material suffers gradually from fracture failure,which coincides with the engineering practice.

From the results as shown in Fig.7,based on the least squares method,the undetermined coefficients of the functional relation between CTOD and Δεpare fitted,which eventually determined the CTOD equation for assessing center-through cracked plate based on accumulated plastic strain at crack tip.The fitted CTOD equation is as:

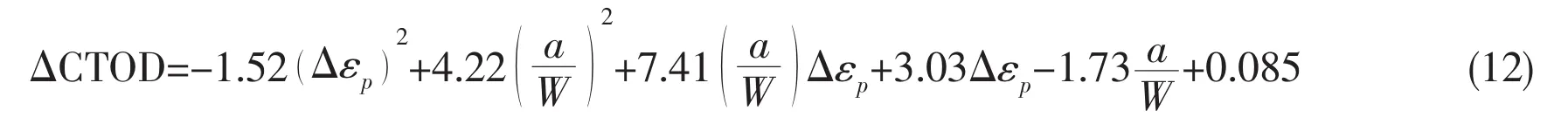
4 Conclusions

In this paper,through the theoretical analysis and finite element numerical simulation,the important elasto-plastic fracture performance parameter CTOD is analyzed for the infinite plate with central-through crack under cyclic loadings.The influences of mean stress and crack length on CTOD are discussed.Besides,based on accumulative plastic damage theory,a CTOD evaluation equation is put forward in account of accumulative plastic strain.The conclusions of the paper are drawn as follows:

(1)Plastic strain is accumulative in the local field of crack tip under LCF loading;the accumulative plastic strain increases gradually and stabilizes eventually as the cyclic times increasing.

(2)The study reveals that crack length,stress amplitude and mean stress have obvious influence on the relationship curve of CTOD vs.accumulative plastic strain.Accumulative plastic strain and CTOD increases as stress amplitude and mean stress increasing.CTOD increases gradually as mean stress increasing when stress amplitude keeps unchanged.

(3)When mean stress and stress amplitude keep unchanged but crack length increases, CTOD increases with accumulative plastic strain increasing.

Because of the limited length of the paper,we have only discussed the two main factors of mean stress and crack length.In actual situation,there are other influence factors,such as stress ratio R of the cyclic load,material hardening exponent n,and size effect.These need to be investigated in further study.

[1]Hutchinson J W.Fundamentals of the phenomenological theory of nonlinear fracture mechanics[J].Journal of Applied Mechanics,1982,49:103-197.

[2]Dugdale D S.Yielding of steel sheets containing slits[J].Journal of the Mechanics and Physics of Solids,1960,8:100-108.

[3]Yaowu S,Siying S,Hidekazu M,et al.Finite element analysis on relationships between the J-integral and CTOD for stationary cracks in welded tensile specimens[J].International Journal of Pressure Vessels and Piping,1998,75:197-202.

[4]Jiang Cuixiang.Research on fracture and crack arrest in ship structures[D].Wuhan:Huazhong University of Science and Technology,2005.

[5]Potirniche G P,Daniewiez S R.Analysis of crack tip plasticity for microstructuralIy small cracks using crystal plasticity theory[J].Engineering Fracture Mechanics,2003,70:1623-1643.

[6]Wu F W,Ibrahim R N,Das R,et al.Fracture toughness for CNT specimens from numerically obtained critical CTOD values[J].Theoretical and Applied Fracture Mechanics,2009,52:50-54.

[7]Chen Jingjie.Strength analysis method research of cracked ship structure[D].Dalian:Dalian University of Technology, 2011.

[8]Chen Jingjie,Huang Yi.A study on evaluation method of crack tip reverse plastic zone size for the center cracked steel plate model under tension-compression cyclic loading[J].Engineering Fracture Mechanics,2015,133:138-151.

[9]Schwalbe K H.The crack tip opening displacement and J integral under strain control and fully plastic conditions estimated by the engineering treatment model for planes tress tension[J].Fracture Mechanics:ASTM,Philadelphia,1994,24:636-651.

[10]Linkens D,Formby C L.A strain-based approach to fracture assessment-example applications[C]//Proceedings of Fifth International Conference on Engineering Structural Integrity Assessment.Cambridge,EMAS,2000:45-52.

[11]Jayadevan K R,Østby E,Thaulow C.Strain-based fracture mechanics analysis of pipelines[C]//Proceedings of International Conference on Advances in Structural Integrity.Bangalore,2004.

[12]Shimanuki Hiroshi,INOUE,Takehiro.Study on the CTOD estimation method of the crack in stress concentrated area[J]. Japan Welding Association Conference Proceedings,2007,25(l):230-237.(in Japanese)

[13]Bjerke S L,Scultori M.DNV’s strain-based fracture assessment approach for pipeline girth welds[C].Proceedings of the International Offshore and Polar Engineering Conference,ISOPE,2011,21:690-697.

[14]Yi D K,Xiao Z M.One elastic-plastic fracture behavior of a bi-layered composite plate with a sub-interface crack under mixed mode loading[J].Composites Part B:Engineering,2014,60:60-73.

[15]Østby E,Jayadevan K R,Thaulow C.Fracture response of pipelines subject to large plastic deformation under bending[J]. International Journal of Pressure Vessels and Piping,2005,82:201-215.

[16]Zhang Y M,Xiao Z M,et al.Strain-based CTOD estimation formulations for fracture assessment of offshore pipelines subjected to large plastic deformation[J].Ocean Engineering,2014,91:64-72.

[17]Hu Guijuan.Plastic behavior of metals under tension-torsion loading-experimental and numerical reaserch on yield surface evolution[D].Qinzhou:Guangxi University,2012.

[18]Landgraf R W,Morrow J.Determination of the cyclic stress-strain curve[J].Journal of Materials,1969,4(1):176.

[19]Qian Yi,Cui Weicheng.An approach for predicting fatigue crack growth based on the cumulative damage theory and elasto-plastic stress field of crack tip[J].Journal of Ship Mechanics,2012,16(8):954-961.

[20]Budden P J.Failure assessment diagram methods for strain-based fracture[J].Engineering Fracture Mechanics,2006,73: 537-552.

基于累积递增塑性变形的船体裂纹板断裂韧性研究

邓军林1a,b,2，杜 波2，杨 平1a,b，陈 远1b

（1a.武汉理工大学 高性能船舶技术教育部重点实验室；b.交通学院，武汉 430063；2.钦州学院 机械与船舶工程学院船舶与海洋工程系，广西 钦州535000）

裂纹尖端张开位移（CTOD）是评估结构材料韧性以及分析低周疲劳破坏引起的裂纹扩展的重要参量。文章结合Dugdale模型，以裂纹尖端累积塑性应变为控制参量，提出了一个循环载荷下含裂纹船体板的CTOD计算模型；利用有限元法模拟了裂纹尖端累积塑性应变、平均应力、裂纹长度等相关因素影响；结合最小二乘法拟合出了基于累积塑性应变、平均应力比以及裂纹长度的两阶多项式。文中基于累积塑性应变的CTOD计算模型为正确评估循环载荷下船体板的累积塑性破坏提供了一种新途径。

中心裂纹板；循环载荷；低周疲劳；累积塑性破坏；CTOD

TG113.25 U661.42

A

邓军林（1983-），男，武汉理工大学交通学院博士研究生；

TG113.25 U661.42

A

10.3969/j.issn.1007-7294.2016.06.010

1007-7294（2016）06-0748-10

杜 波（1979-），男，钦州学院机械与船舶工程学院讲师；

杨 平（1955-），男，武汉理工大学交通学院教授，博士生导师；

陈 远（1992-），男，武汉理工大学交通学院硕士研究生。

Received date：2016-04-10

Founded item:Supported by The National Natural Science Foundation of China(Grant No.51479153); the Fundamental Research Funds for the Central Universities(Grant No.2015-yb-004)

Biography:DENG Jun-lin(1983-),male,Ph.D.student,E-mail:junlin.deng@163.com;

DU Bo(1979-),male,lecturer/tutor of Qinzhou University,E-mail:dubo_332@sina.com;

YANG Ping(1955-),male,professor/tutor,E-mail:pyang@whut.edu.com;

CHEN Yuan(1992-),male,graduate student,E-mail:chendayuans@163.com.