对共振态核子衰变过程的计算∗

张旸，沙依甫加马力达吾来提

(新疆大学物理科学与技术学院，新疆乌鲁木齐830046)

0 引言

核子激发谱的研究是强子物理的重要课题，因为它对夸克模型是一个深度的检验．它是强子内部的相互作用信息的一个重要窗口．BES，CLAS，GRAAL，MAMI等实验组围绕核子共振态的存在、质量、衰变总宽度、各衰变分支比等重要物理量进行了大量实验测量[1−9]，为组分夸克模型[10]等理论模型的检验提供了实验依据．经过对照，许多组分夸克模型预言的核子共振态没有在实验中观测到[11]，对实验与理论同时提出了问题．

核子及其激发态内部的强相互作用属于中低能量范围，在这一能量范围里，由于耦合常数的增加，微扰QCD已经不能直接适用.而格点QCD由于当前计算机计算能力的限制，难以将夸克质量设定为实际质量而不得不外推，影响了它的彻底应用[12]．因此发展强相互作用的有效理论以处理衰变问题并对强子谱进行分析是很有必要的．有效拉式量方法就是在这样一种背景下产生的[13]．它对于整理强相互作用衰变实验数据、分析强子的性质都具有重要的价值．

有效拉氏量方法是场论中微扰方法的唯象运用，将复合粒子也按照基本粒子的方式去处理，对低能范围的强相互作用过程可以获得定性的认识．通过与实验测得的散射截面或衰变宽度比较，定出耦合常数．再通过这样得到的耦合常数，去预测相同性质的过程的散射截面或衰变宽度，与实验比较，便可确知方法的正确性．本文运用此方法计算了向基态的ω衰变，确定了相应的耦合常数．可以用以计算同种性质的衰变过程．

1 方法

场论处理散射、衰变等粒子物理过程首先要写出粒子之间的相互作用拉式量，它可以决定反应过程的几率振幅．有效拉式量方法也要先得到所研究粒子间的相互作用拉氏量．由于光子(γ)是人们认识较为深入的基本粒子，核子共振态与它的相互作用拉氏量是较易写出的．通过模型假设，可以确定有复合粒子在内的相互作用拉式量的基本结构，再由实验使之精细化．Vector Dominance Model(VDM)[14]就是这样一个模型，在中低能量强相互作用过程里得到广泛应用．

通过Vector Dominance Model(VDM),可由N∗Nγ的相互作用拉氏量得到N∗Nω的相互作用拉式量．而前者可以写为[15]:

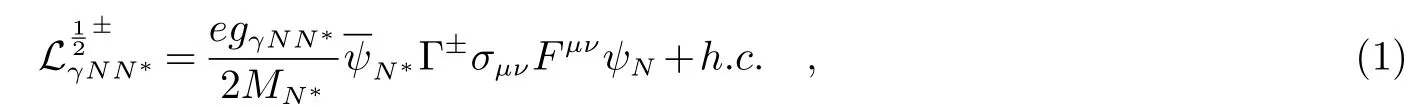
其中gγNN∗为核子共振态与光子之间的耦合常数．是光子的电磁场张量．分别为激发态核子与基态核子的场算符．h.c.表示第二项为第一项的厄米共轭.

自旋更高的核子共振态对应的相互作用拉氏量（例如自旋为

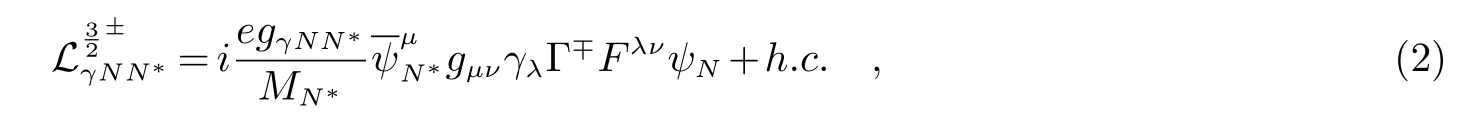
其中是自旋粒子的场算符．正负号对应正负宇称．

VDM模型要求做如下代换以获得N∗Nω的相互作用拉式量：

其中，ωµ为ω粒子的场算符，fω为核子共振态与ω粒子的耦合常数．

因此，对自旋宇称分别为正、负的核子共振态有：

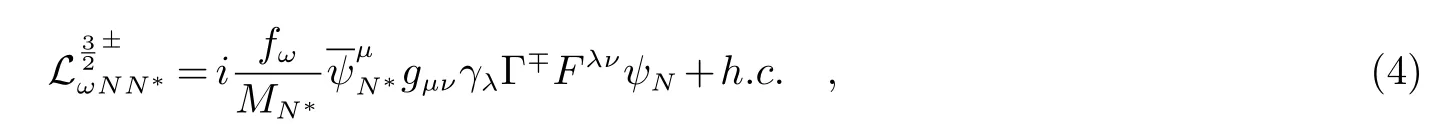
这样，就可以进行相应的衰变宽度的计算．

2 的ω衰变计算

核子激发态有多个衰变道．由于光子没有质量，辐射衰变（放出光子的衰变）是比较普遍的．而ω粒子质量为782MeV，基态核子质量为938MeV,那么，能发生ω衰变的共振态核子的质量至少大于1 720MeV.所以，本文选择N∗(1 875)和N∗(1 900)为计算的对象．

对N∗(1 875)而言，衰变过程为其中N为基态核子．满足宇称守恒、同位旋守恒、角动量守恒．设共振态核子、基态核子、ω粒子的四动量分别为p、p0、k.取质心系，由能量动量守恒，有：

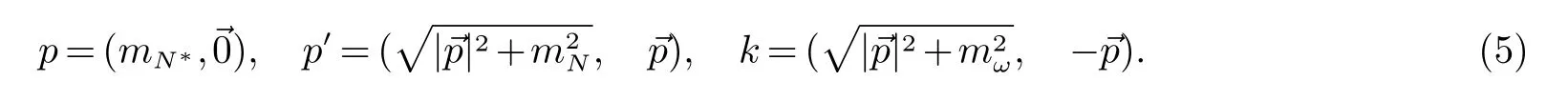
此过程的相互作用拉氏量由（4）式确定，对所研究的衰变过程有贡献的为第二项，化简可得

可得振幅

其中是Dirac旋量，eσν为自旋指标为σ、矢量指标为ν的极化矢量．满足求和规则[17]:

uN∗ν为自旋为3/2粒子的旋量-矢量，它满足自旋求和规则（静系下）[16]：

初态自旋共有四种可能：±3/2,±1/2,可得振幅模平方的平均

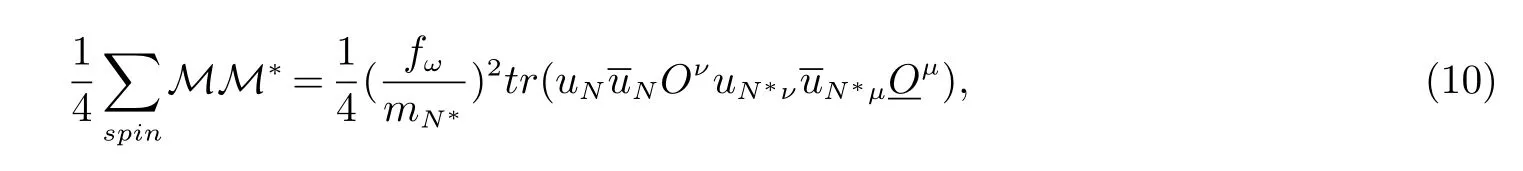
其中

计算矩阵求迹，得

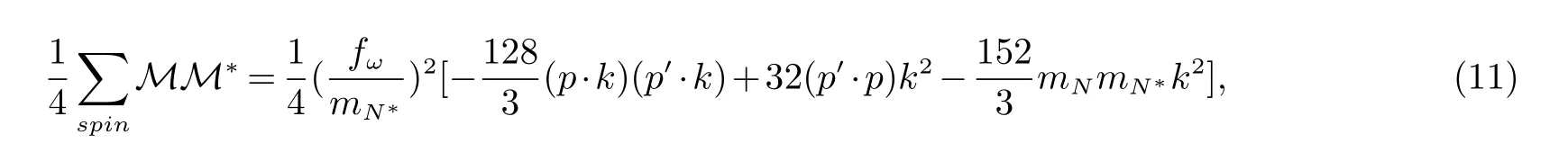
其中

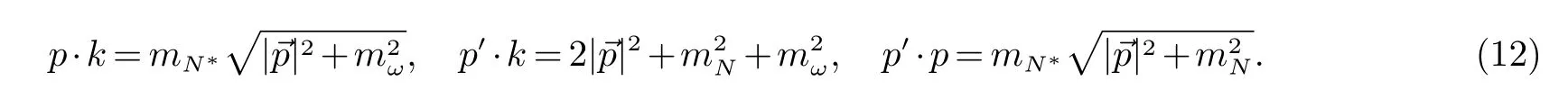
二体衰变宽度公式

其中ρ0为能量动量守恒所要求的末态粒子三动量的模，它由初末态粒子的质量决定：

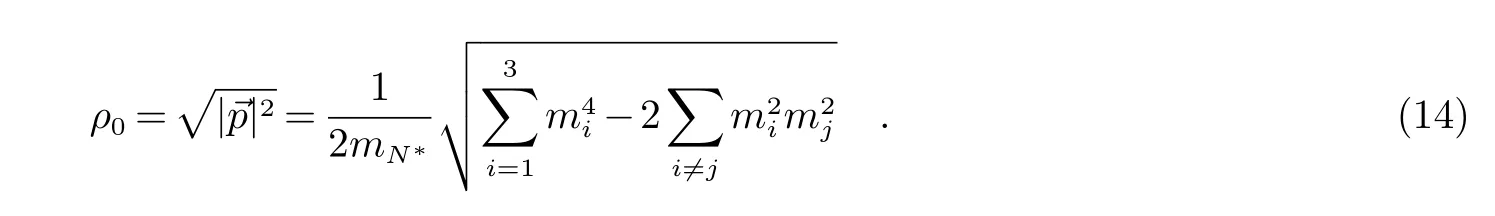
其中m1,m2,m3分别表示基态核子、激发态核子与ω粒子的质量．

共振态核子、基态核子、ω粒子的质量（以MeV为单位）分别为：1 875,938.3,782.7[18].可得ρ0=370.5MeV．带入（11）,（13）式，得衰变宽度

由PDG数据[18],N∗(1 875)衰变总宽度为220MeV,因此衰变宽度的实验值为46.2MeV.与计算值比较，得到耦合常数fω=1.409．

3 N∗(1 900)的ω衰变计算

依然从（4）式出发，只是宇称取正号，会出现γ5=γ0γ1γ2γ3．对所研究的衰变过程有贡献的为第二项：

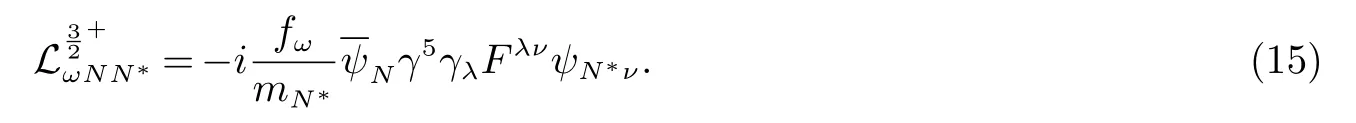
可以得到跃迁振幅：

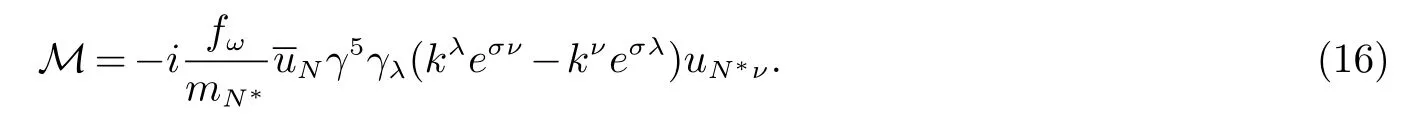
采用计算N∗(1 875)时所用的运动学变量，只需将核子共振态质量从1 875MeV换成1 900MeV.振幅模平方的平均值为：

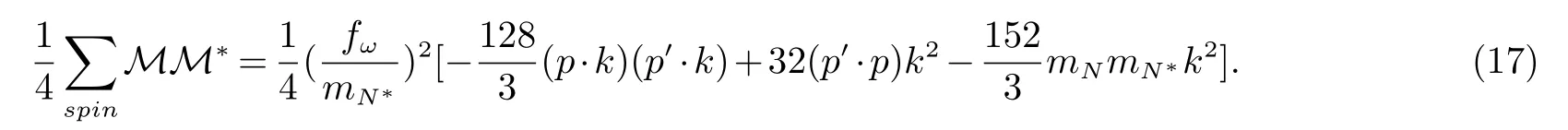
此时，（14）式中的ρ0=485.4MeV.带入（17）式与（13）式可得衰变宽度的计算值为而根据PDG的实验数据[18]，N∗(1 900)衰变总宽度为250MeV,此衰变道的分支比为39%，因此衰变宽度实验值为97.5MeV.这样就定出了对应耦合常数fω=1.723．

4 讨论

本文运用有效拉氏量方法对质量为1 875MeV、自旋为的负宇称核子激发态和质量为1 900MeV、自旋为的正宇称核子激发态的ω衰变进行了计算，由于耦合常数是待定的，所得衰变宽度就成为耦合常数的函数．通过与实验数据比较，定出了它的取值．计算结果与Titov关于其他核子共振态的计算结果[19]在数量级上一致，不过那里没有给出N∗(1 875)和N∗(1 900)的计算值．计算表明，N∗(1 900)的ω衰变耦合常数略大于N∗(1 875)，二者处于同一量级．

可见，强相互作用低能范围的耦合常数不是一个小量，严格的微扰法是不适用的．但是，唯象的有效拉氏量方法保持了场论的基本思想，对粒子物理过程的描述也与场论大体一致，因此可以得出可测量的物理量，能够定性的分析低能过程，在当前的核子激发谱的研究中会继续发挥作用．

用类似的方法可以得出自旋5/2,7/2的共振态核子向着基态衰变并放出一个介子的过程．高质量的核子激发态要求由更重的粒子衰变出来或是由更高的对撞能量直接产生出来．但无论如何，都增加了实验的难度．粒子数据库中质量接近2GeV的核子激发态的实验数据还比较贫乏，不确定度也较大．这就更需要理论与实验结合起来获得高质量核子激发态的基本信息．在大量增加对强子态的确切知识的基础上，再度回归原理的考虑，寻找其与量子色动力学的联系，同时获得更为精细的强子结构模型．

参考文献：

[1]Mokeev V I,Aznauryan I G,Burkert V D,et al.Recent results on the nucleon resonance spectrum and structure from the CLAS detector[DB/OL].arXiv:1508.04088[Nuclear Experiment][2015-08-17].http://arxiv.org/abs/1508.04088v1.

[2]Aznauryan I G,Burkert V D,Mokeev V I.Nucleon Resonance Transition Formfactors[DB/OL].arXiv:1509.08523[Nuclear Experiment][2015-09-28].http://arxiv.org/abs/1509.08523v1.

[3]Park K,Aznauryan I G,Burkert V D,et al.Measurements ofep→e0π+nat W=1.6-2.0 GeV and extraction of nucleon resonance electrocouplings at CLAS[DB/OL].arXiv:1412.0274[Nuclear Experiment][2014-11-30].http://arxiv.org/abs/1412.0274v3.

[4]Dieterle M,Keshelashvili I,Ahrens J,et al.Photoproduction of pi0-mesons of fneutrons in the nucleon resonance region[DB/OL].arXiv:1403.2617[Nuclear Experiment][2014-03-11].http://arxiv.org/abs/1403.2617v1.

[5]BESIII Collaboration.Study ofJ/ψ→ωp¯p[J].Physical Review D,2013,87.112004:1-8.

[6]Anisovich A V,Burkert V,Klempt E,et al.Helicity amplitudes for photoexcitation of nucleon resonances of fneutrons[DB/OL].arXiv:1304.2177[Nuclear Experiment][2013-04-08].http://arxiv.org/abs/1304.2177v1

[7]Wang D,Pan K,Subedi R,et al.Measurement of the Parity-Violating Asymmetry in Electron-Deuteron Scattering in the Nucleon Resonance Region[DB/OL].arXiv:1304.7741[Nuclear Experiment][2013-04-29].http://arxiv.org/abs/1304.7741v2

[8]Thiel A,Anisovich A V,Bayadilov D,et al.Well-established nucleon resonances revisited by double-polarization measurements[DB/OL].arXiv:1207.2686[Nuclear Experiment][2012-07-11].http://arxiv.org/abs/1207.2686v2

[9]Aznauryan I G,Burkert V D.Electroexcitation of nucleon resonances[J].Progress in Particle and Nuclear Physics,2012,67:1–54.

[10]Foster F,Hughes G.Electroproduction of nucleon resonances[J].Reports On Progress In Physics,1983,46:1445-1450.

[11]Capstick S,Robert W.Quark models of baryon masses and decays[J].Progress in Particle and Nuclear Physics,2000,45:241-331.

[12]Peters K.A primer on partial wave analysis[DB/OL].arXiv:hep-ph/0412069[High Energy Physics-Phenomenology][2004-12-05].http://arxiv.org/abs/hep-ph/0412069.

[13]Oh Y,Ko C M,Nakayama K.Nucleon and∆resonances in KΣ(1385)photoproduction from nucleons[J].Physical Review C,2008,77.045204:1-5.

[14]BES Collaboration.Study ofN∗production fromJ/ψ→p¯pη[J].Physics Letters B,2001,510:75-82.

[15]Benmerrouche M,Mukhopaghyay N C,Zhang J F.Effective Lagrangian approach to the theory ofηphotoproduction in the N*(1535)region[J].Physical Review D,1995,51.3237:1-5.

[16]Behtends E,Fronsdal C.Fermi Decay of Higher Spin Particles[J].Physical Review,1957,106.345:1-7.

[17]Zou B S,Hussain F.Lorentz covariant orbital-spin scheme for the effective N*NM couplings[J].Physical Review C,2003,67.015 204:1-7.

[18]Beringer J.Particle Data Group[J].Physical Review D,2012,86.010001:1-320.

[19]Titov A I.Effective Lagrangian approach to the omega meson photoproduction near threshold[DB/OL].arXiv:nucl-th/0205052[Nuclear Theory][2002-05-19].http://arxiv.org/abs/nucl-th/0205052v1.