Dynam ic Pre-ultim ate Strength Evaluation of Containership based on a 2D M odified Hydroelasticity M ethod in Extrem e W aves

LIU Wei-qin,PEI Zhi-yong,WU Wei-guo,SUZUKI Katsuyuki

(1.Departments of Navel Architecture,Ocean and Structural Engineering,School of Transportation,Wuhan University of Technology,Wuhan 430063,China;2.Department of Systems Innovation,Graduate School of Engineering,the University of Tokyo,Tokyo 113-8656,Japan)

Dynam ic Pre-ultim ate Strength Evaluation of Containership based on a 2D M odified Hydroelasticity M ethod in Extrem e W aves

LIU Wei-qin1,PEI Zhi-yong1,WU Wei-guo1,SUZUKI Katsuyuki2

(1.Departments of Navel Architecture,Ocean and Structural Engineering,School of Transportation,Wuhan University of Technology,Wuhan 430063,China;2.Department of Systems Innovation,Graduate School of Engineering,the University of Tokyo,Tokyo 113-8656,Japan)

Extreme waves have led to many accidents and losses of ships at sea.In this paper,a 2D modified hydroelasticity method is proposed as a means of studying the dynamic pre-ultimate strength of a containership instead of post-ultimate strength when traversing extreme waves,while considering the ultimate strength of the ship.Traditional ultimate strength evaluations are undertaken by a quasi-static assumption and the dynamic wave effect is not considered.And,the dynamic response of a ship as induced by a wave is studied on the basis of the hydroelasticity theory so that the nonlinear structural response of the ship cannot be obtained for large waves.So,a 2D modified hydroelasticity method,which takes the coupling between time-domain waves and the nonlinear ship beam into account,is proposed.This method is based on a hydroelasticity method and a Smith method that combine the wave load and the structural nonlinearity.A dynamic reduction in rigidity related to deformation could influence the strength and curvature of a ship’s beam;So,it is input into a dynamic hydrodynamic formula rather than being regarded as a constant structural rigidity in a hydroelastic equation.A number of numerical extreme wave models are selected for computing the modified hydroelasticity,such that large deformations occur and nonlinear dynamic VBM is generated when the ship traverses these extreme waves.Four important extreme wave patterns such as maximum wave height, regular wave height,wave speed,and wave length ratio are changed to study their influence on modified hydroelastic results including nonlinear dynamic VBM and deformational angle at midship,and the modified hydroelastic results are computed and compared with results obtained with the hydroelasticity method,some differences are observed and conclusions are drawn.

dynamic pre-ultimate strength;2D hydroelasticity;Smith method; extreme wave;nonlinear VBM;angle

0 Introduction

The conventional tendency in ship engineering is to evaluate structures based on theirultimate strength,requiring that the ultimate strength of hull girders be evaluated according to the Common Structural Rules(CSR)for Tankers and Bulk Carriers,as specified by the International Association of Classification Societies,Ltd.,(IACS,2006).Many researchers have been pursuing a means of developing an efficient and accurate method of evaluating the ultimate strength of hull girders.Most approaches to computing ultimate strength have been based on static methods.Once ultimate strength of ship is reached,most accidents involving ships have resulted from with a dynamic extreme wave.Pre-ultimate strength denotes the strength still unreached the ultimate strength point while post-ultimate strength means that the strength beyond the ultimate strength point.It is general practice to study pre-ultimate strength of ship for the society of naval architecture engineering and its related rules.So this paper just calculates dynamic pre-ultimate strength of a ship instead of post-ultimate strength in extreme waves or other giant waves by using a 2D modified hydroelastic method.

‘Extreme waves’are more precisely defined as waves with a height more than twice the significant wave height.Furthermore,an extreme wave differs from regular head waves in that it is a single wave.Peliniovsky et al[1]cataloged major marine accidents around the world,and found that at least 22 super-carriers had been lost because of encounters to extreme waves between 1969 and 1994,causing 525 fatalities.He performed several computations of wave loads encountered in the Pacific and the Atlantic.Haver et al[2]recorded an extreme wave at the Draupner platform in the North Sea,providing indisputable evidence that such waves exist.While the significant wave height was 11.92 m,the maximum wave height reached 25.63 m. To understand the physical mechanisms related to such extreme waves,Waseda[3]and Minami[4]have been studying how such waves are formed by simulating extreme waves in a laboratory tank,waves were generated while referring to wave simulations performed with a nonlinear numerical wave tank program,NWT2D.

Traditional hydroelastic theory cannot model the nonlinear structural response of a ship to extreme waves,and the most popular static methods for calculating the nonlinear strength of a ship do not address the dynamic wave problem.Yamamoto et al[5]proposed a time-domain 2D hydroelastic method to calculate the motions and longitudinal strength of a ship as it traverses in waves,while taking the specially nonlinear slamming force was into consideration. However,this method cannot be used to compute the dynamic nonlinear structural response of a ship when faced with in an extreme wave.Masaoka et al[6]proposed a numerical approach to analyze the collapse of a ship’s hull girder when traversing an extreme wave,which was based on a structural analysis system that they had developed.The dynamic FEM system can consider a ship’s longitudinal collapse behavior,whereby the nonlinear fluid forces acting on a ship’s hull were calculated using the Ursell-Tasai method.This paper considers fluid forces acting on ship’s hull by using finite boundary method.Iijima et al[7]proposed a modified hydroelasticity method for a model test,whereby two rigid segments are connected by plastic hinges of different rigidities,rotational angle at a midship section.Different from scale model of above modified hydroelasticity method of Iijima,this paper uses an actual containership to consider the ship collapse due to an extreme wave.Interaction and coupling between in ship structureand waves is also addressed.Xu et al[8]conducted a number of experimental investigations into the collapse behavior of a box-shape hull girder subjected to extreme wave-induced loads, some sacrificial specimens with circular pillar and trough shapes which respectively show different bending moment-displacement characteristics were mounted to compare the dynamic collapse characteristics of the hull girder in waves.And then the post-ultimate strength behavior of the hull girder including the global deformation and motions under extreme wave induced loads are studied by Xu et al[9].Masaoka and Okada[10]used a FEM beam analyzing system to investigate longitudinal collapse behavior by considering the interaction between structural and fluid non-linearity,the collapse behavior of the cross sections of the hull girders is expressed as non-linear bending moment-curvature relationship,an important research direction is guided to modified hydroelasticity.Pei et al[11]developed a total simulation system combining load calculation and structural collapse analysis applied to simulate progressive collapse behaviour of a single-hull Kamsarmax type bulk carrier,the applicability to structure system,high accuracy and sufficient efficiency of ISUM had been demonstrated,but coupling between ship structure and waves are not considered.Liu et al[12]used a strip code to calculate the wave loads of a containership when it transverses extreme waves,and then,these wave loads were applied to a nonlinear dynamic FEM model to obtain the nonlinear dynamic VBM and angles at midship.Liu et al[13]proposed a modified hydroelastic method to evaluate ship nonlinear dynamic strength of ship beam in extreme waves,regarding ship structure as a pure elasto-plastic beam with sulciform section,no buckling effect of ship girder is considered while Liu et al[14]considers the interaction and coupling between in ship structure and waves,a simplified progressive collapse method taking the buckling effect of ship structure into account is combined into the 2D modified hydroelasticity method.

Although FEM was used to calculate nonlinear dynamic strength of ship induced by large waves,we have to face some problems due to FEM.Computational efficiency is too slow and computational cost is too large for shell/solid FE model when ship’s nonlinearity is considered,so the FEM beam model is only choice as Ref.[10]for the modified hydroelastic problem.FEM needs a fixed boundary condition to calculate strength of ship so that the large ship motions induced by extreme waves are not obtained,even dynamic problems to balanced loads, the boundary conditions are added only to suppress the rigid body motion(fix only 6DOFs), which does not lose generality,present commercial codes do not supply a function to account for the wave-structure interaction.This method that is capable of considering 2D modified hydroelasticity was developed by combining the hydroelasticity and Smith method in this paper,the computational efficiency is improved,the interaction and coupling between the ship structure and large waves were studied using a simplified progressive collapse method that accounts for the buckling effect of ship structure,and a FEM beam module is used to calculate the vary ship beam modal shape by varying rigidity of ship beam in this method.At last, extensive extreme wave patterns are analyzed for their influence on nonlinear dynamic strength and large deformation.

1 Theoretical background

1.1 Overview

Hydroelasticity method has been solving elastic response of ship structure in waves.However,this method can not compute dynamic nonlinear structural response of ship in extreme waves.In addition,simplified progressive collapse method(Smith method) has always been simple but efficient method to analyze the progressive collapse behavior of ship girder under longitudinal bending,static ultimate strength can be obtained,but the static method can not analyze the nonlinear dynamic collapse behavior of ship girder in time-domain extreme waves.In this paper,Smith method and 2D hydroelasticity method are integrated to develop a 2D modified hydroelasticity method,this method considers plasticity and buckling nonlinearities of ship section,rigidity of ship beam which is dependent on deformational curvature is alterable rather than constant value in hydroelastic theory,so nonlinear dynamic strength and large deformation can be obtained.Fig.1 shows methodology of modified hydroelasticity method.

1.2 2D Hydroelasticity theory

Fig.1 Methodology of hydroelasticity-plasticity method

A ship can be modeled as a non-uniform free-free beam,and is often assumed to be a Bernoulli-Euler beam.A right-handed coordinate system O（ x0,y0,z0）is fixed in space.The（x0,y0）plane corresponds to the surface of the water,and Z0is directed downwards.Another right-handed coordinate system O x,y,（）z moves forward at a constant speed U,equal to the speed of the ship,and the origin o coincides with a point on the surface of the water,dropped perpendicularly from the aft of the ship.Here,x corresponds to the forward motion of the ship and z is vertically downwards.At the initial time t=0,the two coordinate systems coincide.In terms of the incident waves,it was first considered that a regular wave with an amplitude of ζ0propagates in the negative x direction.Fig.2 shows the coordinate system of the 2D modified hydroelasticity method.For an infinitesimal segment,d x,we can apply the following equilibrium formula.

Fig.2 Coordinate system of the 2D modified hydroelasticity method

where M=vertical bending moment;F=shear force;fe=external force;m=mass per unit length of ship;and w=vertical deflection including elastic-plastic and rigid deflection.Moreover,the vertical bending moment M can be expressed as

where η=equivalent structural damping coefficient;E=Young’s modulus;and I=section moment of inertia.The product term EI is called the‘rigidity of the ship’.Substituting Eq.(2)into Eq. (1),gives Eq.(3),as follows:

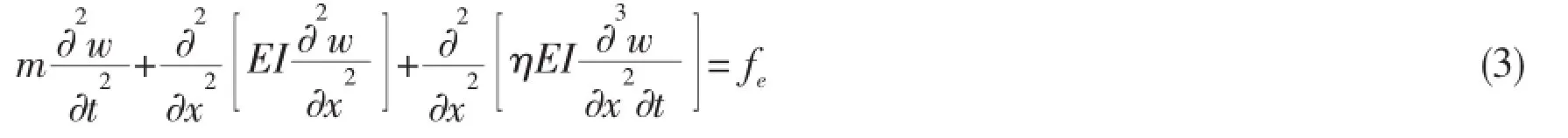
Eq.(3)defines the hydroelastic formula equilibrium.Here,the external force feincludes the wave damping force fr,the weight of the ship fg,the restoring force fs,and the hydrodynamic force fm′.

where the hydrodynamic force fm′takes the hydrodynamic effect of a wave on the ship into account.Even extreme wave,this force remains dominant.Yamamoto et al[5]derived the hydrodynamic force equation presented in Eq.(5).This takes the slamming effect and wave nonlinearity into account.

where MHis added mass derived by the boundary element method,Eq.(5)includes the slamming force component,fslam.

The second part of the hydrodynamic force is the damping force,which is proportional to the speed V:

where N（ x,t）is wave-making damping coefficient per strip which is different by section changing,it is also obtained by using the boundary element method.

The restoring force is given by the following Equation:

The inertial force is given by the following equation:

The force of the ship’s weight due to gravity is expressed as follows:

In addition,the modified hydroelasticity method combines the progressive collapse method with hydroelastic theory.The quasi-static method is used to determine the structural section bending moment and rigidity.The rigidity is determined from the following equation:

where EIpis the nonlinear rigidity,Mpis the nonlinear elastic-plastic bending moment,and w″is the curvature of the section.The relationship between the rigidity and curvature is determined using the progressive collapse method.Moreover,as the rigidity changes,the natural modal shape can be calculated to obtain the renewed vertical deflection wp.The vertical deflection wpshould be satisfied with a boundary condition of free-free.This is expanded by superposing a series of the structural natural modal shape.

where Wj（x）which is structural natural dry modal shape.So the deflection up can be expressed from the mode shapes of a free-free beam.Eq.(12)corresponds to modal superposition,which is not suitable for a nonlinear 3D model.Because buckling may occur with a 3D ship model as it traverses an extreme wave,the deformed shape will be abnormal as long as buckling occurs,making modal superposition inapplicable to the 3D model.However,as this study considers a beam model,it is assumed that the beam model does not incur any buckling,and its deformed shape is normal.

The angle deformation can be addressed by using differential equation of global deflection wp.

The beam rigidity is reduced to consider its capacity to resist deformation under the influence of an extreme wave,so that modal superposition can be applied to a beam model with 2D modified hydroelasticity.The dynamic rigidity,EIpwhich is related to the curvature and modified modal shape,is substituted into Eq.(3).

Eq.(12)is substituted into Eq.(3)to give a dynamic modified hydroelastic equilibrium formula,as given by Eq.(14).This gives the plastic effect,and the added mass and wave-damping coefficient are obtained by using the 2D finite boundary element method.

Eq.(15)involves the term of inertia force matrix［M］,the term of damping force matrix［C］,the term of stiffness force matrix［K］and the term of external force matrix［F］,all matrix of Eq.(15)are expressed as from Eq.(16)to Eq.(19).

The elements of the matrix are as above,the subscript of i or j denotes the number of natural modals,with the first two modals being the rigid ship motions,and the subsequent modals being the flexibility modals.Once the initial conditions are set,the increments can be obtained for a time series by using a numerical integration scheme such as the Newmark-β method.

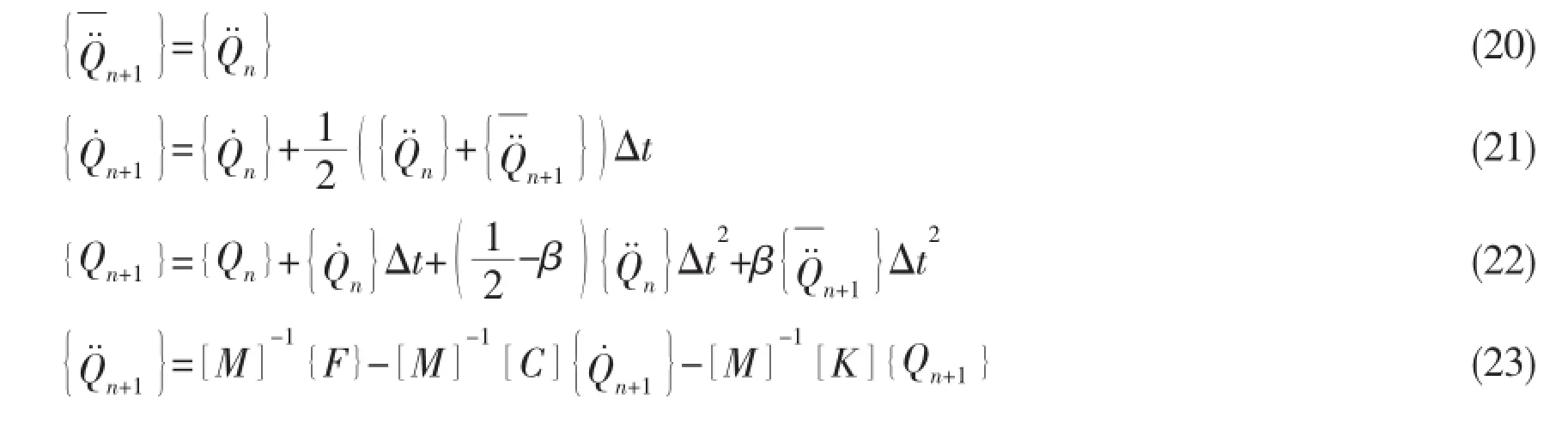
As long as the acceleration term satisfies the iteration condition,the calculation continues to next time step.ε is iterative permissible error.

In this paper,the modified hydroelasticity method is verified for its convergence to determine the number of the integral points.Convergence is verified by using the relative acceleration convergence rate as Eq.(25)whenis just satisfied the iteration condition as Eq. (24)at the iteration step of n+1.

2 Containership model and com putation of ultimate strength

2.1 Containership model

The final objective of this study is to compute nonlinear dynamic strength for a containership in a simulated extreme ocean wave. For this reason,a 500TEU containership is introduced to access its modified hydroelastic computation and wave load.The main principal dimensions of 500TEU container ship are summarized in Tab.1.And the body plan of 500TEU containership is presented in Fig.3.

In this paper,a module for calculating modal shape of FEM beam is used.The wave lengths of all extreme waves would be defined as being equal to the ship length because VBM is the largest so that the condition is the most dangerous.The deformational shape of the ship beam is highly dependent on the wave length.Even if the first flexuous natural mode was assumed to be dominant when the wave length was set such that it was equal to the ship length,former ten flexuous natural modes are applied to superpose the deformational shape of ship in the extreme waves in the study.Therefore,it is sufficient to present the deformational shape of ship as the former ten flexuous natural modes.Fig.4 shows ten flexuous modal shapes of ship and their natural frequencies.

Fig.3 Body plan of 500TEU container ship

Tab.1 Principal dimensions of ship model

Continue Tab.1

Fig.4 Former ten flexuous modal shapes of ship

Fig.5 Ship weight distribution

This computation is carried out based on an assumption that ship is under design full loading whose draft line is designed loading line.Fig.5 shows the weight distribution of 500-TEU containership.Generally,maximum weight is distributed around the middle part of ship due to the loading of cargo while less weight is appeared at two ends of ship.For the same reason,weight distribution requires the corresponding strength and rigidity distribution.In fact,no matter rigidity or the moment-curvature relation is different along ship length,maximum rigidi-ty appears at midship.Fig.6 presents the elastic rigidity(EI)distribution of 500-TEU containership in elastic stage.

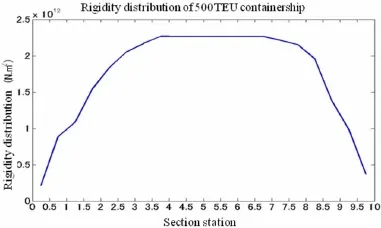
Fig.6 Ship elastic rigidity distribution

2.2 Ultimate strength of 500TEU containership

For reasons of high efficiency and low computational cost,the progressive collapse method has been applied to the computation of the ultimate strength of a ship’s girder.In this study, structural nonlinearity was considered based on the computation of the progressive collapse method,with a flat structural section of a ship being divided into different stiffened elements according to their collapse failure modes,plasticity,and buckling.

The code for the simplified progressive collapse method was programmed to calculate the ultimate strength and determine the relationship between the bending-curvature and rigiditycurvature for a 500TEU containership.Ideal elastic-plastic steel material was used,with a yield stress of 2.35e+008 Pa.Plasticity was taken into account,and the buckling collapse behavior of the stiffened plate elements was considered under compression.In this calculation,the relations of bending-curvature and rigidity-curvature are different along the ship length.Each relation of rigidity-curvature dominates the strength at each strip though it is a great of possible that ship collapse is appeared at midship.Fig.7 shows a structural section of a midship sec-tion of a 500TEU containership and the stress distribution of the structural elements under ultimate sagging strength.The Smith method is used to calculate the ultimate strength,and the three typical stiffened elements(A,B,and C)shown in Fig.7 are assumed to buckle under pressure.Element A represents plate element,element B represents the ordinary stiffened element with angle steel,and element C represents the stiffened element with a T section bar.

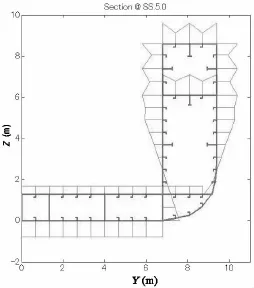
Fig.7 Stress distribution of structural section

Fig.8 Relationship between average strain and average stress of three stiffened elements

The Fig.8 shows the relationship between the average strain and average stress of the three stiffened elements.In Fig.8,relative stress σ/σYmeans stress divided by yield stress and relative strain ε/εYdenotes strain divided by yield strain.This relationship is as stated in the Common Structural Rules for Tankers and Bulk Carriers.

The ultimate bending moments are presented as follows:

where Ms is the ultimate sagging bending moment,which occurs when the curvature is equal to 6.842 0e-04(1/m).Mh is the ultimate hogging bending moment.The curvature for each bending moment is plotted in Fig.9.It can be seen that the ultimate sagging bending moment is smaller than the ultimate hogging bending moment.It is known that the deck is further from the neutral axis than the keel of the ship,such that buckling of the deck occurs when the ship is experiencing sagging bending,but bottom buckling cannot occur easily in the hogging bending case.

Fig.9 Bending moment-curvature of 500TEU containership at midship

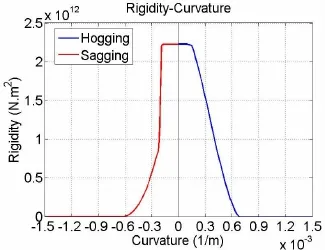
Fig.10 Rigidity-curvature of 500TEU containership at midship

The sectional rigidity is calculated through the application of Eq.(7).The sectional rigidity in the elastic stage is EI=2.26e+012（Nm2）,falls in the elasto-plastic stage,becomes infinitely close to zero at the point corresponding to the ultimate bending moment,and then becomes negative.In the case of sagging bending,when the curvature of a section exceeds 2. 013 0e-04,that section of the ship’s beam enters the elasto-plastic stage.Fig.10 shows the rigidity-curvature curve,from which it can be determined that the rigidity remains constant while the ship is in the elastic stage but falls rapidly when the ship enters the elasto-plasticstage,ultimately falling to zero at the point corresponding to the ultimate bending moment.It is known that the load falls beyond the ultimate strength point while the sectional rigidity becomes negative.This negative rigidity results in the reduction of ship strength further.However,this paper just studies the dynamic pre-ultimate strength,the post-ultimate strength is not studied in this paper.So the negative rigidity of ship is not integrated in the modified hydroelastic code.

2.3 Extreme wave models

A numerical wave tank code NWT2D(New Wave Tanker 2D)performed in some previous studies is used to compose numerical extreme wave models.The program NWT2D was developed by National Maritime Research Institute in Japan.Extreme wave generation is performed by wave superposition of linear numerical regular wave and numerical focusing wave,focusing wave is generated in specific position and time,focusing wave amplitude and energy superposition are coincided with regular wave amplitude and energy to compose extreme wave which has a higher wave height.Fig.11 shows the numerical extreme wave by superposition of numerical regular wave and focusing wave,(a)is numerical regular wave elevation,(b)is numerical focusing wave elevation,(a)is superposition with(b)to generate(c),(c)is numerical extreme wave.In this study,numerical extreme wave model is also linear wave.

Fig.11 Numerical extreme wave by superposition between numerical regular wave and focusing wave

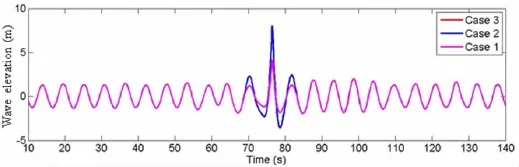
Fig.12 Wave elevation profile of containership at midship

Three extreme wave models(Case 1,Case 2 and Case 3)are presented in Tab.2 as typical extreme wave model,their regular waves are kept similarly to make sure computational comparability,regular wave height is 2.8 m while the ratio of wave length to ship length(Lw/ L)is equal to 1.0.Extreme wave height is paid a close attention,three different focusing wave heights are used to change extreme wave heights such as 6.0,11.4 and 11.6.The ratios ex-treme wave height divided by D(molded depth)are 0.7,1.33 and 1.35.These three extreme wave Cases are defined to indicate three typical strength condition of elastic strength,elastoplastic strength and ultimate strength.Time-domain profiles of three extreme wave models are presented in Fig.12.

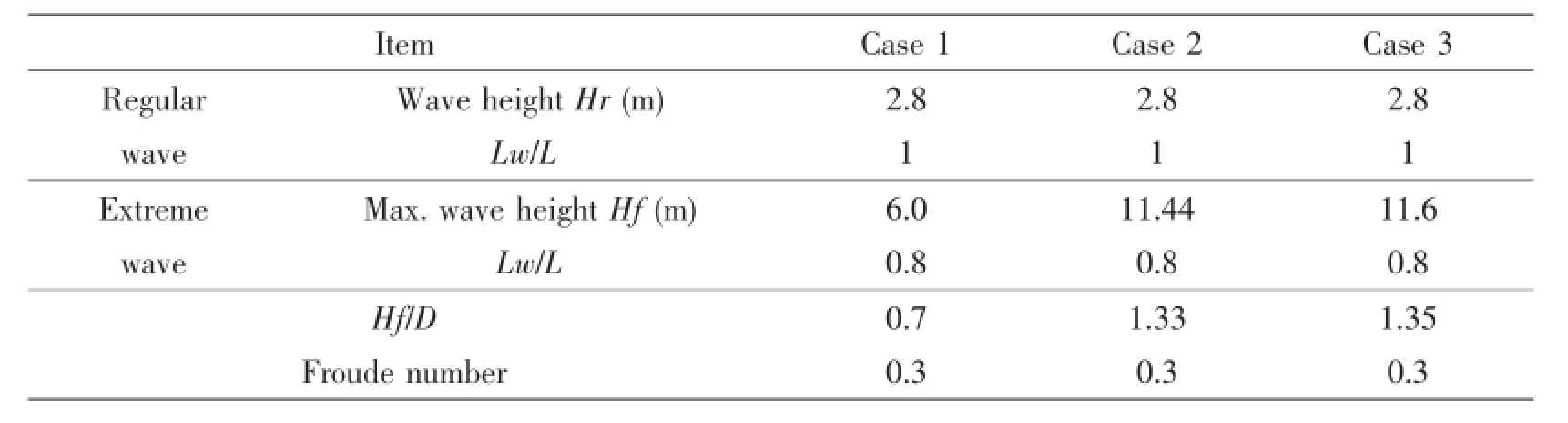
Tab.2 Typical extreme wave model

3 Calculation of modified hydroelasticity

In this paper,a method for calculating modified hydroelasticity is proposed to enable the study of the nonlinear dynamic response of a containership to the extreme waves described above.Firstly,the convergence of modified hydroelasticity is discussed by remeshing ship beam to different number of elements along ship length.And then a number of computations including deformational angle and VBM at midship were performed using the TPSLAM modified hy-droelastic code,they are plotted and compared with the calculations of hydroelasticity,so that the difference between the nonlinear and linear dynamic results can be obtained transparently.In addition,the course of any collapse and the reasons for the collapse are studied for extreme waves.

Fig.13 Midship angle obtained with modified hydroelasticity and hydroelasticity

A parameter of angle derived from Eq.(9)is used to manifest itself as deformation of the ship’s beam,it is solved from differential equation of global deflection wp by length.The angle at the midship section warrants close attention.The low rigidity of the beam generates a large deformational angle.Fig.13 shows the angle curves obtained with the modified hydroelasticity and hydroelasticity methods at the midship section when subjected to the three extreme waves described above.Fig.13,(a)shows that there is no difference between the two methods,(b)indicates that the modified hydroelasticity method generates a larger angle deformation than the hydroelasticity method,with a residual deformational angle(rs2=0.075°)being generated after the first large peak.Next,(c)shows a much greater deformation,with the maximum angle obtained with the modified hydroelasticity method being 1.103 6 degrees with a residual angle(rs3=0.665 9°),while the maximum angle obtained with the hydroelasticity method alone has a very small value of 0.345 degrees.

Fig.14 Sagging bending moment and elasto-plastic unloading

It is observed from Fig.13(b)and(c)that residual deformational angles are resulted in. The modified hydroelasticity method considers residual deformation due to elasto-plastic unloading.As to above three extreme waves,sagging bending results in large deformation and residual deformation.As long as ship enters elasto-plasticity,unrecoverable residual deformation is induced.Fig.14 shows the elasto-plastic unloading routes of Case 2 and Case 3.Residual angle rs2 induced in Case 2 and residual angle rs3 induced in Case 3 are generated due toelasto-plastic unloading.Dynamic modified hydroelastic analysis shown in Fig.13 reveals the residual angles rs2 and rs3 after the top of dynamic angle curves.

Fig.15 VBM as obtained with modified hydroelasticity and hydroelasticity

In this study,the nonlinear vertical bending moment(VBM)is obtained from the calculation of the relationship between the curvature and bending moment,as shown in Fig.9.In previous research,VBM was calculated by using linear hydroelastic code since the structural rigidity is assumed to be constant when using the hydroelasticity method.In this study,VBM was computed by using a modified hydroelasticity method,with the structural nonlinear rigidity of the ship’s beam being regarded as a dynamic time-domain,as determined from the deformational curvature.A large angle occurs when an extreme wave impacts a ship’s beam as shown in Fig.13(c),is calculated by using the modified hydroelasticity method.Therefore,a larger VBM peak is obtained when using the modified hydroelasticity method,in comparison with the hydroelasticity method.Fig.15 presents the VBM curves as obtained with the modified hydroelasticity and hydroelasticity methods at midship points with the above three extreme waves.Fig.15(a)shows the VBM for the Case of CASE 1 at S.S.5.0.It can be seen that results obtained with the hydroelastic-plastic and hydroelastic methods are in very good agreement,meaning that the CASE 1 extreme wave generates only an elastic response from the ship. Next,(b)shows that there is very little difference at the first large peak,but that the VBM as determined using the modified hydroelasticity method is larger than that obtained with the hydroelasticity method,meaning that the extreme Case of CASE 2 produces an elastic-plastic response.Finally,(c)shows a considerable difference for the first large peak,with the maxi-mum VBM being attained at the ultimate sagging bending moment Ms.This implies that in the extreme wave Case of CASE 3,the response is fatal.Both(b)and(c)indicate that the modified hydroelasticity method produces a larger VBM result than the hydroelasticity method when ship beam enters the stage of large deformation.

Fig.16 Hydrodynamic VBM and hydrostatic VBM of CASE 3

Fig.17 Models obtained with hydroelasticity and modified hydroelasticity models(t=72 s)

It is obvious from Fig.15(c)that a sharp dynamic VBM peak occurs at time=72 seconds when CASE 3 extreme wave is encountering the ship.It is necessary to analyze the component of the dynamic VBM peak.The wave forces are classified by hydrodynamic and hydrostatic force as Eq.(4)explains,the hydrodynamic component includes wave damping load,inertia load and slamming load,the hydrostatic component is decided by interaction between ship weight and buoyancy.CASE 3 is used to analyze dynamic VBM components,modified hydroelastic VBM and hydroelastic VBM have the same hydrostatic components,and Fig.16 reveals modified hydroelastic VBM,hydroelastic VBM and hydrostatic VBM of CASE 3.It is obvious that no matter modified hydroelastic VBM peak or hydroelastic VBM peak is much larger than the peak of hydrostatic VBM,it indicates that hydrodynamic component plays a dominant role to result in the top of dynamic VBM when extreme wave of CASE 3 is encountering to the ship model.Fig.17 shows models of the hydroelasticity and modified hydroelasticity forextreme wave CASE 3 when time is equal to 72 seconds.By comparing the results obtained with the modified hydroelastic model,a large deformation is generated for hydroelastic-plastic model while the hydroelastic model produces an inconspicuous deformation.In addition,a significant slamming phenomenon happens at the bow of ship,it means a giant impacting force would be generated in upper-forward section,so that the ultimate sagging bending moment is generated at this instant,slamming force is dominant to induce ultimate sagging bending moment,and fatal sagging bending is earlier than hogging bending.

Fig.18 Rigidity distribution of three extreme wave

Fig.19 Time-domain modified hydroelastic model in CASE 1

Fig.18 shows rigidity distribution of three extreme wave when time is equal to 72.0 seconds for above three extreme wave Cases.It is obvious from Fig.18 that the ship rigidity changes greatly along ship length for Cases of Hf/D=1.35 and Hf/D=1.33,the smallest rigidity appears around the midship due to ship collapse is happened,while Case of Hf/D=0.7 does not change the rigidity of ship so that only elastic response of ship is resulted.

The Case of CASE 1 was studied carefully to determine the deformational course of the ship model when struck by the extreme wave.As we know that the CASE 3 wave model consists of a regular wave in its beginning and end parts and an extreme wave in the middle part, the responses for both a regular and extreme wave are obtained.Fig.19 shows a time-domain modified hydroelastic model for the CASE 3 wave.Fig.19 presents six images of the modified hydroelastic model at different times(t=67 s,71 s 72 s,76 s,and 78 s).The images for t=67 s show the model for the regular wave,while the extreme wave begins to pass the ship model, which is elevated at the bow when t=71 s,such that a large deformation is generated when t= 72 s,and then the extreme wave arrives at the stern of the ship,which falls at t=76 s.At t=78 s,the extreme wave has passed the ship model.

4 Discussion on convergence of the 2D method of m odified hydroelasticity

4.1 Discussion on convergence of the method regarding to element number

The calculation results are verified for the method of modified hydroelasticity by discussing its convergence.The way verifying the convergence of the modified hydroelasticity is to change the number of subdivisions of ship beam. Fig.20 shows the number of ship subdivisions (N=10,20,30,40 and 50).Relative acceleration convergence rate as Eq.(25)is used to ac-count for the convergence of modified hydroelasticity.Fig.21 shows the relative acceleration convergence rates as the number of ship subdivisions is changed from 10 to 50 while extreme wave model is CASE 3 which wave parameters are revealed in Tab.2.Fig.21 reveals three curves of relative acceleration convergence rates when time is equal to 67.8 s,72.0 s and 91.9 s.It is observed from Fig.21 that relative acceleration convergence rates are reducing as the number of ship subdivisions is increasing,and the relative acceleration convergence rate is in close proximity to zero when the number of ship subdivision is 50.According to the tendency of three curves shown in Fig.21,it is indicated that the calculation model with large number of ship subdivision has smaller relative acceleration convergence rate.It means that the convergence of the modified hydroelasticity is affirmative.Fig.22 shows the ratio of VBM at midship to sagging ultimate bending moment Ms when the number of ship subdivisions is changed.Also three time steps(67.8 s,72.0 s and 91.9 s)are chosen to be shown.Nearly zero VBM,regular VBM peak and extreme maximum VBM peak are induced at these three time steps.It is observed that nearly zero values are resulted when the number of ship subdivisions is changed at time step of 67.8 s,VBM of time step of 72.0 s has a significant increasing since the number of ship subdivisions from 10 to 20 but the ratio of VBM to Ms almost keeps to 1.0 after the number of ship subdivisions is 20.The VBM of time step of 91.9 s has a very tiny growth since the number of ship subdivisions is increased to 20.It is indicated that the number of ship subdivisions has a tiny effect on VBM results since it is increased to 20,and extreme wave model of CASE 3 leads to sagging ultimate bending moment after N is equal to 20.Therefore, the number of ship subdivisions is determined as 20 in this paper based on the consideration of computational cost of the code.

Fig.20 Number of ship subdivisions

Fig.21 Relative convergence rate as number of ship elements is changed

Fig.22 VBM/Ms as number of ship elements is changed

4.2 Discussion on convergence of the method regarding to mode number

In addition,the convergence of the 2D modified hydroelasticity regarding to the number of mode is discussed.The way discussing the convergence of the modified hydroelasticity is to change the number of ship mode.In this paper,the numbers of ship modal involving Nm=1,2, 3,4,5,7,10,15 are used to discuss the applicability of modal method while extreme waveCase is fixed at CASE 3.The Nm-th modal shapes are superposed to obtain ship deformation and ship’s rigidity is varying.Each relative acceleration convergence rate is recorded when the number of ship modal involving Nmis equal to 1,2,3,4,5,7,10 and 15.Fig.23 shows the relative acceleration convergence rates as the number of ship mode is changed to 1,2,3,4, 5,7,10 and 15.It is observed from Fig.23 that the relative convergence rate is notched up small increases when the number of mode is increasing,the relative convergence rate is not sensitive if the number of modal is larger than 10.On the whole,the relative convergence rate increases with the number of modal.Similarly,the ratio of VBM at midship to sagging ultimate bending moment Ms regarding to the number of modal is discussed.Fig.24 shows that the ratio of VBM at midship to sagging ultimate bending moment Ms when the number of mode is changed.It is obvious from Fig.24 that the Max.VBM/Ms keeps constantly as long as the number of mode is larger than 3 though it is increasing slightly when number of mode is between 1 and 3.It is indicated that the number of mode has no effect on maximum VBM as long as it is larger than 3.It means that former three modal shapes are dominant for ship deformation regarding to extreme wave CASE 3,because the CASE3 in which wave length is close to ship length is significant for global ship deformation instead of local deformation simulated by larger modes.

Fig.23 Relative convergence rate as number of mode is changed

Fig.24 VBM/Ms as number of mode is changed

5 Structural evaluation of 500TEU containership in extreme waves

In order to be applicable to ship designing,as many as wave parameters are studied as well to get general conclusions.The main selection for extreme wave case is supposed to cover most extreme wave patterns,four important extreme wave patterns are considered such as extreme wave height,regular wave height,wave speed and wave length.The four extreme wave patterns are changed to study their influence on nonlinear dynamic strength and deformation of ship.Extreme wave height means the maximum wave height as the mid-part of Fig.12 shows, extreme wave height ratio(Hf/D)which is the ratio of extreme wave height(Hf)to moldeddepth(D)is used to denote the extreme height level.

5.1 Extreme wave pattern for extreme wave height

To study the dynamic strength and evaluate the dynamic pre-ultimate strength,the influence of the wave/height ratio(Hf/D)on the ship’s strength and deformation was studied.In this computation,the regular wave height,Hr,has been determined to be 2.8 m and the Froude number of the encountered wave is determined to be 0.3.According to the computational results obtained with the modified hydroelasticity and hydroelasticity methods,Fig.25 shows the maximum VBM/Ms curve as Hf/D is increasing.The ratio of the maximum VBM to Ms indicates the strength of the ship,Ms is sagging ultimate bending moment.All of the points on the blue curve were calculated using the hydroelasticity method,while the points on the red curve were computed using the modified hydroelasticity method with structural nonlinearity taken into account.It is obvious that there is a great difference between them.It indicates that an actual nonlinear dynamic VBM has an ultimate value,and does not increase infinitely,as the height of an extreme wave height increases.It can be seen that,as long as Hf/D is equal to or greater than 1.35,the modified hydroelastic model reaches an ultimate strength and does not increase infinitely.When Hf/D is around 1.55,the maximum VBM of the hydroelastic model exceeds the value of the ultimate bending moment.In the range of Hf/D from 1.3 to 1.55,there is a difference in spread between the two methods,nonlinear VBM calculated by modified hydroelasticity is larger than linear VBM calculated hydroelasticity.

Fig.25 Max.VBM/Mu curves between hydroelastcity and hydroelasticity-plasticity method

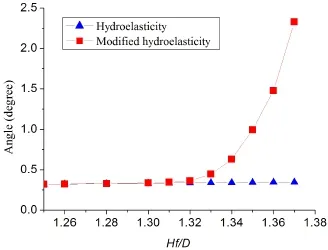
Fig.26 Maximum angles by changing extreme wave height ratio

The difference between the two methods is compared based on another viewpoint of deformational angle,that is taken the ship’s deformation into account.The deformational angle at the midship section(S.S.5.0)was computed.Therefore,the influence of Hf/D on the angle at the midship section was also examined.Fig.26 shows the angle curve at S.S.5.0 as Hf/D is increasing.The blue points denote the hydroelastic computations of angle,and the red points represent the modified hydroelastic computations of the angle.It is obvious that there is a difference in the angle since Hf/D exceeds 1.32.It can be seen that a large deformation is generated with the modified hydroelastic model but that the maximum angle of the hydroelastic model increases almost linearly with small amplitude.

5.2 Extreme wave pattern for regular wave height

An extreme wave pattern for regular wave height(Hr)is studied to investigate its influence on ship ultimate strength and deformation.The regular wave height,whose interval is 0.5 m,is increased between 0.5 m and 5.5 m while other wave patterns are determined as Fr=0.3, and Lw/L=1.In order to investigate the difference of maximum extreme wave height on ship strength,three extreme wave heights(Hf=11.8,10.32,and 6.0 m)are arranged.Fig.27 shows Max.VBM/Ms curves by changing regular wave height while wave Froude number is 0.3 and wave length ratio Lw/L=1,curves of a1 and a2 mean that their extreme wave height is 11.8 m, curves of b1 and b2 denote that their extreme wave height is 10.32 m,curves of c1 and c2 have extreme wave height as 6.0m,red curves denote that their results are calculated by modified hydroelasticity method while blue curves are calculated by hydroelastic method.It is observed that the extreme waves whose maximum extreme wave is 11.8 m and 10.32 m induces the difference between two methods,it implies that large deformation and nonlinear dynamic strength are resulted in,while the extreme wave(Hf=6.0 m)manifests that no difference between two methods,it means that no large deformation is occurred.Although a small increasing tendency of maximum VBM when regular is increased,maximum extreme wave height plays a dominant role on the large deformation and nonlinear strength.As Fig.27 shows,the effect of regular wave height on ship strength and deformation is rather finite compared with maximum wave height.If it can play a significant effect on ship strength,the maximum wave height needs rather enough amplitude.

Fig.27 Maximum VBM s by changing regular wave height

Fig.28 Maximum angles by changing regular wave height

Fig.28 reveals maximum angle at midship while regular wave height is increasing from 0. 5 m to 3.0 m.By comparison between modified hydroelastic and hydroelastic results,the large deformation is generated since regular wave height is 2.0 m for modified hydroelastic computations while the deformational angle is relatively small manifested by hydroelasticity.

5.3 Extreme wave pattern for encountering wave speed

The extreme wave pattern for the encountered wave speed was used to study the influence of the encountered wave speed.Froude numbers are changed to study the influence on shipstrength while other wave patterns are determined as(Hf=11.6 m,Hr=2.78 m,Lw/L=1).Fig. 29 shows the max.VBM/Ms points obtained with the hydroelasticity and modified hydroelasticity methods versus the Froude number,which increases from 0.05 to 0.35 while the wave height ratio Hf/D is fixed at 1.35.It can also be observed that the modified hydroelasticity method produces an ultimate bending moment while the hydroelasticity method does not.Furthermore,the modified hydroelasticity method has a smaller Froude number(Fr=0.3)to make structural entering ultimate VBM while the hydroelasticity method has a larger value of around Fr=0.325 to exceed 1.The VBM difference between the two method occurrs since Fr=0.25.This means that the encountered wave speed has a significant influence on ship strength.Particularly,the use of the modified hydroelasticity method incurs a different effect regarding the encountered wave speed,in comparison with the hydroelasticity method,given that the structural nonlinearity is considered.

The effect of the wave speed on the ship deformation is also taken into account.Fig.30 shows the maximum angle points obtained with the hydroelasticity and modified hydroelasticity methods as the Froude number changes from 0.05 to 0.35.It can be seen that the two methods produce different results,with the deformation increasing gradually up to a large value when the Froude number is 0.25.The ultimate strength is generated when the Froude number is 0.3.

Fig.29 Maximum VBM s by changing Froude number

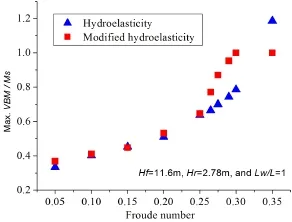
Fig.30 Maximum angles by changing Froude number

5.4 Extreme wave pattern for wave length ratio

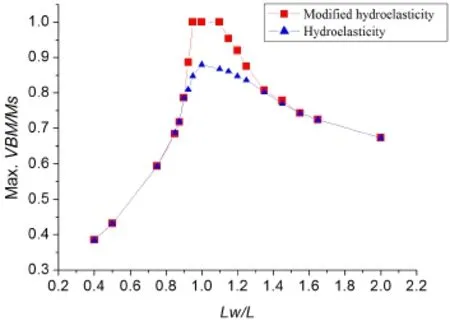
Fig.31 Maximum VBM s by changing wave length ratio

The extreme wave pattern of wave length ratio is discussed to study the strength difference when is changed.The wave length ratio Lw/L denotes the wave length divided by ship length,and wave length ratio is changing from 0.4 to 2.0 while maximum wave height is 13 m,regular wave height is 2.78 m,and Froude number is 0. 3.Fig.31 is maximum VBM/Ms curves by changing wave length ratio.It is seen thatmaximum VBM is occurred around Lw/L=1, maximum nonlinear VBM calculated by modified hydroelasticity arrives ultimate sagging bending moment while maximum linear VBM calculated by hydroelasticity does not arrive the value of ultimate sagging bending moment,the great difference of VBM s occurs in the span around Lw/L=1 where it is from the point(Lw/L=0.9)to the point(Lw/L=1. 35),and ultimate bending moment is generated from the point(Lw/L=0.95)to the point (Lw/L=1.1),other range is the same so that only elastic strength is induced.

Fig.32 shows the maximum angle curves by changing wave length ratio.The wave length ratio is plotted on the horizontal axis,and maximum angle is plotted on the vertical axis,the red curve denotes the maximum angle calculated by modified hydroelasticity while the blue curve means the maximum angle calculated by hydroelasticity,it is obvious that maximum values of angles occur around the Lw/L=1,maximum angles calculated by modified hydroelasticity and hydroelasticity are the same when the wave length ratio is smaller than 0.9 or larger than 1.45,but the angle difference happens when wave length ratio is between 0.9 and 1.45 because the large deformation calculated by modified hydroelasticity appears,and the angles calculated modified hydroelasticity exceed to 1.137°in which ultimate bending moment occurred when the wave length ratio is between 0.95 and 1.1,it also means that the ship is disable to survive between 0.95 and 1.1.

Fig.32 Maximum angles by changing wave length ratio

6 Conclusions

This paper proposed a 2D modified hydroelasticity method which combines Smith method and hydroelasticity method,a number of extreme wave models were selected for modified hydroelastic computations,and a number of computational results were obtained and compared with those obtained with the hydroelastic method.So we can draw the following conclusions:

(1)The modified hydroelasticity method is able to calculate the dynamic nonlinear strength and structural deformation of a ship beam subject to extreme waves.

(2)Nonlinear dynamic strength calculated by modified hydroelasticity has a smaller extreme wave height ratio,regular wave height,and wave speed to make ship arrive the value of ultimate strength of ship than the linear static strength calculated by hydroelasticity,and modified hydroelasticity is easier to result in ultimate strength than hydroelasticity when wave length ratio is around 1.0.

(3)Extreme wave height plays an important role to make ship collapse,while other waveparameters have secondary effects on ship safety because they should combine extreme wave height to determine the ship safety.

The current method considers nonlinear ship structure considering plasticity and buckling effect,beam model is applied in a 2D modified hydroelastic code.It is future work to take into account of 3D effect of modified hydroelasticity,every realistic structural member of ship will be computed in future.In fact,the different ship model has different relation of rigidity(EIp) and curvature which has a important effect on nonlinear dynamic response of ship in the same extreme wave model,it also is another perspective that ship model(nonlinear moment-curvature relation)is changed when extreme wave is fixed.There must be a lot of interesting results to be discussed for further studies.

[1]Peliniovsky E,Kharif C.Physical mechanisms of the rogue wave phenomenon[J].European Journal of Mech.B/Fluids, 2003,22:603-634.

[2]Haver S,Andersen O J.Freak waves:Rare realizations of a typical population or a typical realization of a rare population [C]//Proc.10th International Society of Offshore and Polar Eng Conf.Seattle,USA,1990,3:123-130.

[3]Waseda T,Rheem C K,Sawamura J,Yuhara T,et al.Extreme wave generation in laboratory wave tank[C].Proc.15th International Society of Offshore and Polar Eng Conf.,2005:1-9.

[4]Minam i M,Sawada H,Tanizawa K.Study of ship responses and wave loads in freak wave[J].The Japan Society of Naval Architects and Ocean Engineers,2006.

[5]Yamamoto,Yoshiyuki,Fujino,Masataka,Fukaswa,Toichi.Motion and longitudinal strength of a ship in head sea and the effects of non-linearities[C].Conference of the society of naval architects of Japan.Nov.1978.

[6]Masaoka K,Okada H.A numerical approach for ship hull girder collapse behavior in wave[C]//ISOPE2003.Honolulu, Hawaii,USA,2003:369-375.

[7]Iijima K,Kimura K,Xu W,Fujikubo M.Modified hydroelasticity approach to predicting the post-ultimate strength behavior of ship’s hull girder in waves[J].Journal of Marine Science and Technology,2011,16(4):379-389.

[8]Xu W,Iijima K,Wada R,Fujikubo M.Experimental evaluation of the post-ultimate strength behavior of a ship’s hull girder in waves[J].J Marine Sci.Appl.,2012:34-43.

[9]Xu W,Iijima K,Wada R,Fujikubo M.Parametric dependencies of the post-ultimate strength behavior of a ship’s hull girder in waves[J].J Mar Sci Technol,2012,17:203-215.

[10]Masaoka K,Okada H.A numerical approach for ship hull girder collape behavior in waves[C].Proceedings of ISOPE2003, 2003:369-375.

[11]Pei Z,Iijima K,Wada R,Fujikubo M,et al.Simulation on progressive collapse behaviour of whole ship model under extreme waves using idealized structural unit method[J].Marine Structures,2015:104-133.

[12]Liu W,Suzuki K,Shibanuma K.Nonlinear dynamic response and structural evaluation of container ship in large extreme waves[J].Journal of Offshore Mechanics and Arctic Engineering,2015:64-73.

[13]Liu W,Suzuki K,Shibanuma K.Nonlinear dynamic response and strength evaluation of a containership beam in extreme waves based on hydroelasticity-plasticity method[C].Conference Proceedings of the International Society of Offshore and Polar Engineers,2014,4:652-657.

[14]Liu W,Suzuki K,Shibanuma K.A two-dimensional hydroelastoplasticity method of a container ship in extreme waves[J]. Journal of Offshore Mechanics and Arctic Engineering,2015:84-93.

基于一个二维修正水弹性方法的集装箱船体梁动态前极限强度评估研究

刘维勤1，裴志勇1，吴卫国1，铃木克幸2

（1.武汉理工大学交通学院海洋工程系，武汉430063；2.东京大学工学系研究科系统创成专攻，东京113-8656，日本）

海上极端波因其巨大的波高常常导致船体的极限破坏。该文提出了一个二维的修正水弹性方法来研究一个集装箱船船体梁在极端波中的动态前极限强度。传统的极限强度评估基于准静态方法，没有动态效应被考虑。而船体在波浪下的动态结构响应是基于水弹性方法，传统的水弹性方法并不能计算船体梁的动态非线性强度。该二维修正的水弹性方法考虑时域波浪和非线性船体梁之间的耦合，将水弹性方法和Smith方法结合，用Smith方法计算船体梁的刚度，而其刚度与船体梁的强度和变形曲率有关。所以该时域的非线性刚度被用于修改水弹性方法里的常数项的结构梁刚度。几组极端波模型被用以产生船体梁的大变形和非线性动态垂向弯矩。文中分别采用修正水弹性方法和普通水弹性方法，通过改变四个重要的极端波参数如极端波最大波高、规则波的波高、波速和波长等来研究其对船体梁船中处的大变形转角和非线性垂向弯矩的影响，通过采用修正的水弹性方法计算得来的结果与水弹性方法计算得来的结果相比较，得到了一些差异和结论。

动态极限强度；二维修正水弹性方法；Smith方法；极端波；非线性垂向弯矩；转角

TV131.2

A

刘维勤（1985-），男，武汉理工大学交通学院讲师；裴志勇（1974-），男，武汉理工大学交通学院副教授；吴卫国（1960-），男，武汉理工大学交通学院教授；铃木克幸（1964-），男，日本东京大学工学系研究科教授。

TV131.2

A

10.3969/j.issn.1007-7294.2016.09.005

1007-7294（2016）09-1121-26

Received date：2016-07-22

Foundation item:Supported by National Natural Science Foundation of China:the study of Hydroelasto-plasticity Method of Ship Structure(51509197)

Biography：LIU Wei-qin(1985-),male,lecturer,E-mail:liuweiqin_123@sina.com; PEI Zhi-yong(1974-),female,associate professor.