基于不确定客流的高速铁路列车停站方案优化方法
2016-05-15戚建国
牛 丰, 戚建国, 秦 进
(1. 中南大学 交通运输工程学院,湖南 长沙 410075; 2. 中国铁路总公司,北京 100844;3. 北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044)
列车停站方案是列车开行方案的重要环节,明确列车为旅客提供的服务区间,在列车径路、类别、编组辆数、开行频率确定后,根据客流需求和列车协调配合情况确定各类列车的停站序列[1]。列车停站方案的设置不仅关系到高速铁路的服务质量,而且对于铁路资源的利用效率和经济效益也具有重要影响。
鉴于列车停站方案的重要性,诸多学者针对该问题进行一系列颇有成效的研究。目前,大多数文献将列车停站方案与开行方案的其他子问题一并进行研究[1-2]。文献[1]通过分析列车停站设置和客流换乘选择之间的博弈关系,将基于停站方案的多类用户均衡客流分配模型作为下层规划模型,构建旅客列车停站方案双层规划模型,并设计基于模拟退火算法的启发式算法对模型进行求解;文献[2]将高速铁路系统包含的不确定性和不易量化因素统一用节点服务表示,以节点服务频率、站间服务可达性、单个列车停站次数等作为主要约束条件,构建以总停站次数最少为目标的非线性规划模型,运用停站概率与计算机模拟相结合的方法有效解决模型求解的问题;文献[3]将列车停站次数及相应的停靠车站嵌入列车开行方案中,建立以最小化旅客停站时间、列车虚糜及未满足需求的旅客数量为目标的多目标多层0-1整数规划模型,利用有序组合树方法对模型求解;文献[4]基于区段最大客流密度确定所需最少开行列车数量,提出基于停站方案的旅客列车开行方案优化策略;文献[5]分析列车停站的主要影响因素,从方便旅客出行及减少旅客出行广义费用两方面考虑,建立列车停站方案综合优化模型,并结合列车停站优化问题的具体特点,提出包含初步和综合优化的两阶段优化算法对模型求解;文献[6]分析高速铁路停站方案对列车牵引能耗和旅行时间的影响,以最小列车牵引能耗和最短旅行时间为优化目标,以既有运输供给为约束,建立考虑列车能耗的既有停站方案优化模型;文献[7]分析列车停站与时刻表之间的相互关系,构建列车停站方案与运行图协同优化模型;文献[8-13]对运行图及运行图追踪进行详细论述。
上述文献为探讨高速铁路列车停站方案优化设计方法提供良好的理论基础,但现有研究大多在确定的环境下考虑列车运行组织优化问题,而对停站方案设计中一些不确定因素未能给予充分考虑。实际上,由于旅客出行目的的多样性以及线路上各车站所处地理位置及政治地位的不同,每天乘坐列车出行的旅客明显不同,导致同1条线路上不同车站之间的客流亦有很大差异,从而致使车站上发送、到达客流量具有很大的不确定性。以京沪线泰安站为例, 某3个月的发到客流分布情况见图1。
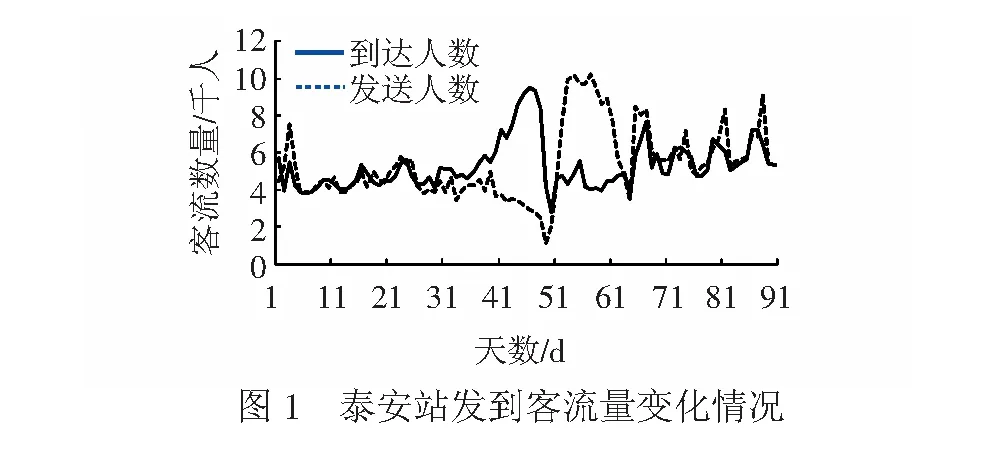
从图1可以明显看到,发到客流量随着时间不同而不断波动,且很难用概率论和数理统计的方法刻画其规律性。车站发到客流随时间变化的波动性和无规律性直接导致车站发到客流量的不确定性。
确定环境下的列车停站优化模型,只是针对某种情况下客流需求优化列车停站策略,难以应对客流需求不断波动情况下的优化决策。忽略铁路运营中客流的不确定性势必导致某些时段内列车有较大虚糜或突发客流需求不能得到满足的情况,从而导致服务水平和运输资源利用效率的降低。因此,探讨基于不确定客流的高速列车停站方案的优化设计,对提高列车服务的鲁棒性和可靠性,规避不确定因素带来的决策风险具有重要的理论和现实意义。
本文拟在既有研究的基础上,从理论研究的角度出发,将高铁车站的发到客流需求描述为不确定变量,构建高速铁路列车停站方案优化问题的机会约束规划模型,并进一步基于不确定理论和方法,将该模型转化为确定的等价类模型后进行求解和计算。
1 问题描述
设图2为某高速铁路线路,S表示线路上车站的集合, |S|表示车站数量。该线各站从左至右依次编号为1,2,3,…,|S|。其中,车站1代表起始站,车站|S|代表终点站,其余编号代表线路中间车站。T表示给定开行方案下运行在该线路上的列车集合,|T|为列车开行列数。下面研究如何合理确定在区段上开行的所有列车的停站方案,要求在尽可能满足客流需求和保障一定服务水平的基础上,优化高速铁路运输资源利用效率。

高速铁路客流需求一直呈现出高度的不确定性。当具备充足的历史数据时,可以考虑采用数理统计方法,将客流需求处理为服从一定概率分布的随机变量;而在缺乏充足样本的情况下,有效的描述方法是将该类数据视为不确定变量进行分析。本文正是基于不确定理论的相关方法,将各车站的发到客流数据处理为不确定变量,建立数学优化模型进行分析。
2 模型构建
2.1 模型决策变量
为清楚的确定列车在每个车站的停站方案,采用如下决策变量确定列车k的停站策略
式中:k、i分别为列车与车站的标号,且k∈T,i∈S。
2.2 模型目标函数
高速铁路列车停站方案对线路的通过能力和运输效率产生较大影响。一般而言,增加列车停站次数将延长列车占用车底的时间,从而增加运营所需的总车底数量、列车因启制动引起的额外能耗、乘务组费用以及车站的额外费用等[3]。因此,在满足旅客需求置信水平的前提下,尽量减少列车停站次数,可以降低运输成本,提高铁路企业经济效益。本文将以最小化列车总停站次数为优化目标,以期用最少的运营成本(即停站次数)满足一定置信水平下的不确定旅客需求。
模型优化目标为
( 1 )
式中:X为决策变量xki组成的向量;F(X)为所有列车总停站次数。
2.3 模型约束条件
列车停站方案必须尽可能满足铁路运输需求并符合相关技术规范。因此,在编制过程中需要考虑一系列系统约束条件,如客流需求约束、停站次数约束等。
(1) 车站发送和接收客流约束
高速铁路运营中,旅客出行目的多样性导致车站发到客流需求的无规律波动。对于车站发到客流量的不确定性,本文将其描述为不确定变量,并采用不确定分布函数进行有效刻画。在此基础上,采用机会约束规划思想,将满足客流需求表示为发到客流需求得到满足的机会达到一定的置信水平,以获得鲁棒性较强的列车停站方案。发到客流需求满足的置信水平约束可分别表示为
∀i∈S
( 2 )

( 3 )
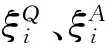
车站发送和到达客流约束是本文模型中最重要的约束条件,也是列车停站方案中首要考虑的因素。其中,约束条件(2)确保每个车站i的旅客发送能力大于该车站客流需求的不确定测度大于给定的置信水平αi;约束条件(3)保证每个车站i接收旅客的能力大于该车站客流需求的不确定测度大于给定的置信水平βi。
(2) 车站所需最少停靠列车数量约束
优化列车停站方案的过程中,若仅考虑各车站发送和接收客流需求约束,则可能导致客流较小的车站停靠列车数量过少。为进一步提高客流需求较小车站旅客出行的便捷性,体现铁路运营的公共服务特点,规定每个车站的最小停站列车数量,以保障车站必要的服务水平,即
∀i∈S
( 4 )
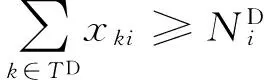
( 5 )

该约束条件可确保每个车站停靠的不同速度列车数量不小于事先确定的阈值。事实上,尽管该约束可能将增加某些列车的停站次数,延长旅客的出行时间,但也最大限度提高铁路服务的均衡性及短途旅客出行的便捷性。
(3) 列车最大停站次数约束
列车停站次数对运输能力和运输效率具有重要影响,停靠较多车站必然将延长列车对车底的占用,大幅度增加列车的总运行时间,降低线路的通过能力。此外,频繁的停站操作也将导致列车不断地启动和制动,产生不必要的能源消耗。从运输服务水平和舒适性方面看,旅客期望在出行过程中尽可能停靠较少的车站,以减少总旅行时间。基于以上分析,模型需要对列车的总停靠次数进行约束。
最大停站次数约束
∀k∈T
( 6 )
式中:Mk为列车k允许的最大停站数量。
显然,该约束确保列车总的停站次数在预先给定的范围之内,从而避免某些列车停靠车站较多(特别是速度等级较高的列车),而另外一些列车停站较少的现象,保证高速铁路运输系统中列车服务的均衡性。
(4) 开行区段约束
实际运营中,由于给定区段内开行的列车不经过该区段以外的其他车站,且给定区段内的所有列车必须从该运行区段的起始车站行至终到车站。
开行区段约束
∀k∈T
( 7 )
xkSk=xkRk=1 ∀k∈T
( 8 )
式中:Lk为列车k开行区段内车站集合,Lk∈S;Sk、Rk分别为列车k在其开行区段内的起始和终到车站。
上述约束保证所有列车按照开行方案中预先设定的开行区段运行,同时不经过既定服务区段之外的车站。
(5) 变量取值约束
变量xki为0-1决策变量,取值约束为
xki∈{0,1} ∀k∈T∀i∈S
( 9 )
2.4 建立模型
根据以上分析,构建基于不确定客流的高速铁路列车停站方案优化模型
(10)
s.t.
∀i∈S
(11)

(12)

(13)
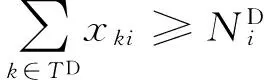
(14)
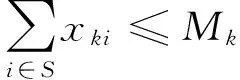
(15)
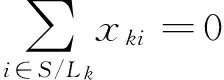
(16)
xkSk=xkRk=1 ∀k∈T
(17)
xki∈{0,1} ∀k∈T∀i∈S
(18)
3 确定性等价类模型
3.1 不确定理论及其定义
不确定理论为有效处理难以获取精确信息的不确定决策问题提供良好的数学基础,已被成功应用于多个实际领域,如交通运输领域[14]、金融领域[15]和图论领域[16]等。为便于后续分析和阐述,下面简要介绍不确定理论中的部分定义、公理及推论。
定义1不确定测度
假设Γ为非空集合,L是Γ上的σ-代数。每个元素Λ∈L被称为1个事件,M{Λ}表示事件Λ发生的置信水平。如果M{Λ}满足以下3条公理,则称为不确定测度[17]。
(1) 常规性:对于全集Γ,有M{Γ}=1;
(2) 自对偶性:对于任意事件Λ,有M{Λ}+M{Λc}=1。其中,Λc为Λ的对立事件;
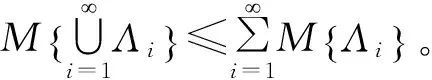
事实上,不确定测度可理解为不确定事件发生的信度,而不是频率,他取决于每个人对该事件的认知程度,具有一定的主观性。
定义2不确定空间
假设Γ为非空集合,L为Γ上的σ-代数,M为不确定测度,则称三元组M(Γ,L,M)为不确定空间[17]。
定义3不确定变量
不确定变量ξ是从不确定空间(Γ,L,M)到实数集的1个可测函数。即对任意实数Borel集B,集合{ξ∈B}={γ∈Γ|ξ(γ)∈B}是L中的1个事件[17]。
不确定空间和不确定变量的定义与概率论中的概率空间和随机变量的定义形式类似。但由于不确定测度与概率测度有本质区别,不确定变量的内涵也不同于随机变量。
定义4不确定分布
不确定变量ξ的不确定分布Φ定义为Φ(x)=M{ξ≤x}。其中,x为任意实数[17]。
定义5常规不确定分布
如果1个不确定分布的逆函数Φ-1(α)对于任意的α∈(0,1)存在且唯一,则称该不确定分布为常规不确定分布[17]。
定义6逆不确定分布
假设不确定变量ξ服从常规的不确定分布Φ(x),则称逆函数Φ-1(x)为不确定变量ξ的逆不确定分布[17]。
在决策过程中,可以采用不确定分布的形式刻画任意的不确定变量。如果不确定变量ξ的不确定分布如下所示,则称ξ为之字形不确定变量,记为Z(a,b,c)。其中,a、b、c为实数且满足a (19) 显然,之字形不确定变量的不确定分布为分段函数形式,其中每段图像均为线性函数。在实际应用中,之字形不确定变量是较为常用的非精确数据的表示方式[17]。 定义7关键值 假设ξ为不确定变量,且α∈(0,1],则称ξsup(α)=sup{r|M{ξ≥r}≥α}为ξ的α-乐观值;ξinf(α)=inf{r|M{ξ≤r}≥α}为ξ的α-悲观值[17]。 下面,重点介绍2个机会约束的等价定理,相关结论对于构建机会约束规划模型的等价类起着关键的作用。 推论1之字形不确定变量Z(a,b,c)的逆不确定分布为[17] Φ-1(α)= 利用上述定义、定理及推论,将本文前面提出的不确定客流下高速铁路列车停站方案的机会约束规划模型转化为确定性等价类模型,以便于模型的求解和计算分析。 ∀i∈S (20) (21) 当且仅当 ∀i∈S (22) (23) (24) (25) 基于以上分析,将前面提出的机会约束规划模型式(10)~式(18),重新构建为0-1整数线性规划模型 s.t. 式(13)~式(18)、式(22)~式(23) 与原模型式(10)~式(18)相比,上述线性模型的目标函数和约束条件均不变,仅原模型中的置信水平约束(11)~约束(12)被替换为线性约束(22)~约束(23),由此模型中的所有约束条件均为线性表达式。上述线性模型可直接通过MATLAB调用GUROBI优化软件进行求解。 上述模型中置信水平αi和βi为预设参数,其值的选取是由决策者预先给定。乐观决策者可设定较小的参数,而悲观决策者则需选取较大参数以保证约束在较高置信水平下成立。此外,对于该参数的选择,可给出如下定理: 证明:假设D′和D*分别为两组参数可行解的集合。由于对任意X∈D*,有 ∀i∈S (26) (27) 从而说明D′⊃D*成立。可得以下结论 (28) 定理得证。 以武汉—广州段高速铁路为背景,假设列车开行对数和开行区间已知的条件下,应用构建的模型优化确定列车停站方案。 为简化问题,仅考虑从武汉到广州的单向线路,共15个车站、开行80列列车。根据客流需求,整个线路划分为3个区段,即武汉—广州南、武汉—长沙南、长沙南—广州南。其中,武汉到广州南开行50列高速铁路动车组列车(G字头列车)和2列动车组列车(D字头列车),武汉到长沙南开行2列D字头列车,长沙南到广州南开行18列G字头列车和8列D字头列车。简单起见,对于各类列车的发送和接收旅客能力,假定每一列车在各车站的发送和接收旅客能力相同,均设定为150人,同时,对于车站发送和到达旅客需求得到满足的置信水平均设置为90%。 对于列车停站次数,设定高速铁路动车组列车的最大停站次数为10次,动车组列车为站站停列车。为保障沿线客流需求较小车站的服务水平,假定每站至少需有2列G字头列车停靠。 考虑到高速铁路实际运营过程的复杂性,各站发送和到达旅客需求服从的分布形式及具体数值,一般由相关专家根据经验给出。为数据处理方便,本文将其设定为服从之字形分布的不确定变量,见表1。 表1 车站发送和到达客流需求 人 将所建模型转化为确定等价类模型后,在CPU为I3-4130、内存为4 G的Windows 7系统中,使用MATLAB调用GUROBI优化软件对模型求解,计算时间均不大于1 s。 在满足各站客流需求的不确定测度均大于90%的条件下,可得到列车停站方案,见图3。 从图3可以看出,除起始和终到车站外,该停站方案中所有列车共停站215次。由于动车组列车为站站停列车,且每个车站均至少有2列G字头列车停靠,保证旅客需求较少车站的服务水平。此外,在该停站方案中,大部分高速铁路动车组列车停站次数相对较少,从而减少旅客在车站等待时间,缩短长距离出行旅客的总出行时间,有效提高直达率。 αi、βi,i∈S为预先确定的服务置信水平,不同的置信水平对应于不同的旅客出行需求满足程度。为探讨不同置信水平的取值对列车停站方案的影响,本文设定αi、βi分别为0.1、0.2、…、1.0,并对模型进行求解,结果见表2。 表2 不同置信水平的列车停站次数 由计算结果可知,随着不确定置信水平αi、βi的增加,列车在除起始和终到车站外停靠车站的数量呈现上升趋势以保证更多的旅客需求得到满足。特别当αi、βi取值为0.1时,列车在车站外最优停站次数为207次,而当αi、βi取值为1.0时,最优停站次数则增加到215次。一般而言,较大的置信水平将满足更多的旅客需求,相应的停站次数也将增加,运营过程中列车的虚糜也可能增大;相反,较小的置信水平则可能导致较多的客流需求不能被满足,从而降低旅客的满意度。另外,列车停站次数的变化亦与给定各站发送和到达旅客需求服从的分布形式及具体数值有关。较大的分布区间,表明客流需求具有更强的不确定性,导致随着给定置信水平的变化,列车停站次数的变化更为明显;反之,则变化较小。为此,在实际应用中αi和βi取值应由决策者依具体情况合理选择。 本文将车站的发到客流量处理为不确定变量,构建不确定客流需求下的高速铁路列车停站方案问题的机会约束规划模型,并进一步基于不确定理论的相关知识将其转化为确定的等价类模型,在此基础上利用GUROBI优化软件模型求解。最后,通过武汉—广州段高速铁路数据进行验证。结果显示,模型及算法具有良好的优化质量和计算效率。 实际运营中,列车停站方案的设计与旅客出行选择之间存在相互影响,且乘务组排班计划、时刻表的优化等问题与停站方案之间也存在必然联系。因此,如何将这些问题与列车停站方案结合为一体进行优化将是下一步研究的主攻方向;其次,列车停站优化模型中考虑OD客流需求以及每列车上客流的分配也是需重点思考的问题;另外,列车停站方案优化问题本质上为多目标决策问题,进一步探讨列车能耗、满载率以及旅客舒适度、可达性等指标也将是今后研究的主要内容。 参考文献: [1] 邓连波,史峰,周文梁.旅客列车停站设置方案优化[J].中国铁道科学,2009,30(4):103-107. DENG Lianbo, SHI Feng, ZHOU Wenliang. Stop Schedule Plan Optimization for Passenger Train[J]. China Railway Science, 2009, 30(4): 103-107. [2] 李得伟,韩宝明,李晓娟,等.基于节点服务的高速铁路列车停站方案优化模型[J].铁道学报, 2013, 35(6): 1-5. LI Dewei, HAN Baoming, LI Xiaojuan, et al. High-speed Railway Stopping Schedule Optimization Model Based on Node Service[J]. Journal of the China Railway Society, 2013, 35(6): 1-5. [3] 张拥军, 任民, 杜文. 高速列车开行方案研究[J]. 西南交通大学学报, 1998, 33(4): 400-404. ZHANG Yongjun,REN Min,DU Wen.Optimization of High Speed Train Operation[J].Journal of Southwest Jiaotong University, 1998, 33(4): 400-404. [4] 漆昕, 熊坚. 基于停站方案的旅客列车开行方案优化研究[J]. 铁道运输与经济, 2012, 34(12): 43-57. QI Xin, XIONG Jian.Research on Optimization of Passenger Train Operation Diagram Based on Stopping Diagram[J]. Railway Transport and Economy, 2012, 34(12): 43-57. [5] 黄鉴, 彭其渊. 高速列车停站优化问题的两阶段求解算[J].西南交通大学学报, 2012, 47(3): 484-489. HUANG Jian, PENG Qiyuan.Two-stage Optimization Algorithm for Stop Schedule Plan of High-speed Train[J]. Journal of Southwest Jiaotong University, 2012, 47(3): 484-489. [6] 冯旭杰, 孙全欣, 冯佳,等. 高速铁路既有停站方案优化模型[J]. 交通运输工程学报, 2013, 13(1): 84-90. FENG Xujie, SUN Quanxin, FENG Jia, et al. Optimization Model of Existing Stop Schedule for High-speed Railway[J]. Journal of Traffic and Transportation Engineering 2013, 13(1): 84-90. [7] YANG Lixing, QI Jianguo, LI Shukai, et al. Collaborative Optimization for Train Scheduling and Train Stop Planning on High-speed Railways[J/OL]. Omega, http://dx.doi.org/10.1016/j.omega.2015.11. 003. [8] YANG Lixing, LI Keping,GAO Ziyou. Train Timetable Problem on a Single-line Railway with Fuzzy Passenger Demand[J]. IEEE Transactions on Fuzzy Systems 2009, 17(3): 617-629. [9] YANG Lixing, LI Keping, GAO Ziyou, et al. Optimizing Trains Movement on a Railway Network[J]. Omega,2012, 40: 619-633. [10] YANG Lixing, ZHOU Xuesong, GAO Ziyou. Credibility-based Rescheduling Model in a Double-track Railway Network: a Fuzzy Reliable Optimization Approach[J]. Omega,2014, 48: 75-93. [11] LI Shukai, YANG Lixing, LI Keping, et al. Robust Sample-data Cruise Control Scheduling of High-speed Trains[J]. Transportation Research Part C: Emerging Technologies,2014, 46: 274-283. [12] LI Shukai, YANG Lixing, GAO Ziyou. Coordinated Cruise Control for High-speed Trains Movements Based on a Multi-agent Model[J]. Transportation Research Part C: Emerging Technologies,2015, 56: 281-292. [13] LI Shukai, YANG Lixing, GAO Ziyou. Adaptive Coordinated Control of Multiple High-speed Trains with Input Saturation[J]. Nonlinear Dynamics,2016,83(4):2 157-2 169. [14] YANG Lixing, LIU Pei, LI Shukai, et al. Reduction Methods of Type-2 Uncertain Variables and Their Applications to Solid Transportation Problem[J]. Information Science, 2015, 291: 204-237. [15] CHEN Xiaowei. American Option Pricing Formula for Uncertain Financial Market[J]. International Journal of Operations Research, 2011, 8(2): 32-37. [16] GAO Yuan, YANG Lixing, LI Shukai. On Distribution Function of the Diameter in Uncertain Graph[J]. Information Science, 2015, 296: 61-74. [17] LIU Baoding. Uncertainty Theory[M]. Berlin: Springer-verlag, 2007: 11-114.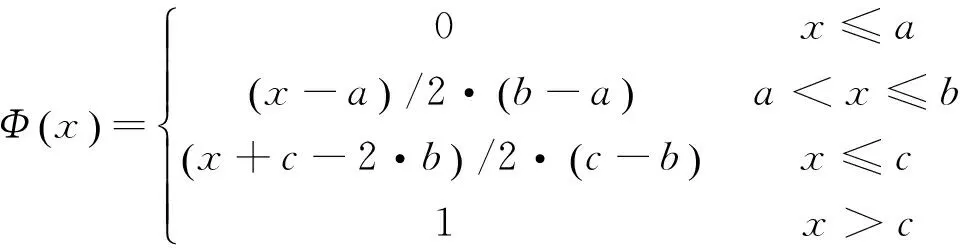
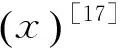
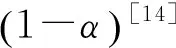


3.2 确定性等价类模型


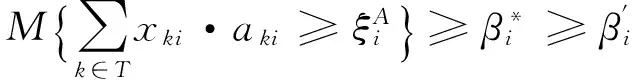
4 算例计算及分析
4.1 模型输入数据

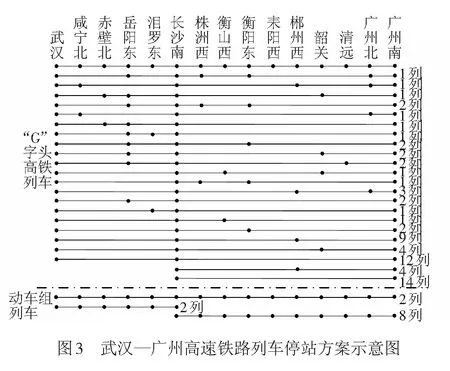
4.2 停站方案计算分析
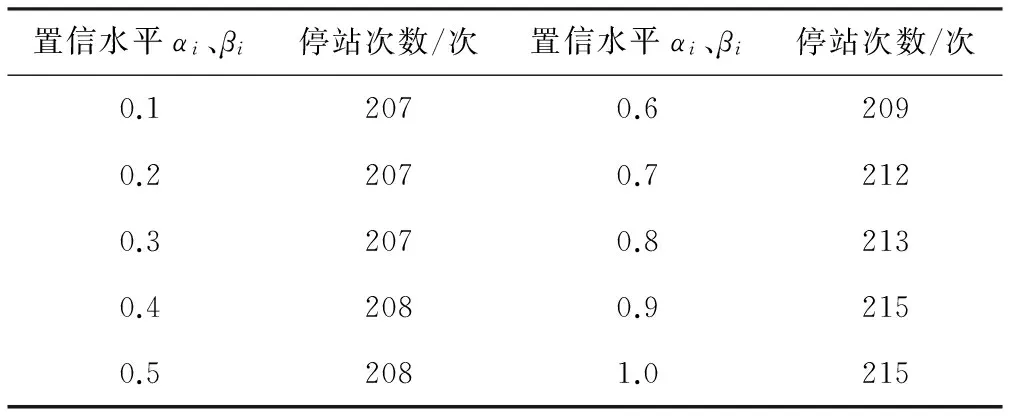
4.3 停站次数的灵敏度分析
5 结束语
