改进的基于局部模块度的社团划分算法

王天宏 武星 兰旺森

摘要：针对大多复杂网络社团划分算法不能快速发现最优节点加入社团的问题，提出一种利用节点亲密度的局部社团划分算法。引入节点亲密度的概念量化社团与邻居节点的关系，按照节点亲密度由大到小选择节点加入社团，最后以局部模块度为指标终止局部社团扩展。在真实网络和人工仿真网络进行实验，并与基于信息压缩的随机游走算法等4种典型社团划分算法相比较，所提算法划分结果的综合评价指标（F1score）和标准化互信息（NMI）均好于比较算法。实验研究表明，所提算法具有较好的时间效率和准确度，适用于大规模网络社团划分。

关键词：复杂网络；社团划分；节点亲密度；模块度；人工合成网络

中图分类号：TP393.02 文献标志码：A

Abstract：Focusing on the problem that the best neighbor nodes of the communities can not accurately be found in most local community detection algorithms， an improved local community detection algorithm was proposed based on local modularity. The concept of node intimacy was introduced to quantify the relationship between the community and the neighbor nodes by the algorithm， and the nodes were selected into the communities according to the node intimacy in descending order. In the end，the extension of the local community was terminated by the local modularity index. Compared with the four kinds of typical community detection algorithms such as the random walk algorithm based on information compression， the algorithm was applied in the real networks and the artificial simulation network. The comprehensive evaluation indexs （F1score） and Normalized Mutual Informations （NMI） of the results are better than comparison algorithms. The experiments show that the algorithm has better efficiency and accuracy， and is very suitable for community detection in a large scale network.

Key words：complex network； community detection； node intimacy； modularity； synthetic network

0 引言

许多自然界和人类社会中的复杂系统可以用网络或图来描述。网络的研究关键是要了解网络结构和这些复杂系统的功能。一个常见的复杂网络的特点是社团结构，即社团内节点彼此连接要比社团外的节点更紧密。社团结构的识别方法在各科学研究领域备受关注[1-5]。

大多数社团检测方法主要是基于整个网络结构，不能用于某些类型的网络，如社会网络、万维网，因其规模较大而且是动态变化的网络，对网络结构不能充分了解。于是学者们提出一些局部社团划分方法，可通过网络的局部知识检测网络社团结构[6-11]。这些算法在发现精确完整的社团上已经取得了很大进步。但是，这些现存方法或多或少都存在一些限制，比如，文献[6]方法因数据存储方法的局限性，无法应用于大规模网络； 文献[7]方法过于依赖事先定义的参数，而这些参数往往难于获得； 文献[8]方法凝聚新顶点的条件过于严格，完整的社团很难获得；

文献[9]方法的效率对于源节点选择很敏感，结果也存在过多的特例。受Clauset算法[7]启发，本文提出了一个局部社团划分新算法，以局部度最大节点作为开始节点，以特定顺序的搜索潜力顶点，通过计算局部社团模块度确定最终的社区结构。本文算法并不同于Clauset算法对每个邻居节点计算其局部模块度，而依据顶点和社团之间的亲密度，以亲密度大小排序，选择最优节点加入社团，此举提高了算法效率和精度。

1 相关定义

局部度最大节点通常有这样的属性，如果两个局部度最大节点的度不相等，那么它们不相邻[13]。因此局部度最大节点往往分散分布在网络中。仅当局部度最大节点度值相同时才相邻。LFR基准网络（LancichinettiFortunatoRadicchi benchmark graph）是当前社团划分研究中应用最为广泛的数据集。本文以LFR基准网络实验验证了局部度最大节点比全局度最大节点更适合作为网络社团的初始节点。LFR基准网络主要包括以下参数：n为网络节点个数；k是在网络中的节点的平均度；maxk是网络中节点度的最大值；minc表示最小社团所含节点数目；maxc 最大社团所含节点数目；mu是混合参数，是节点与外部社会的节点连接的概率，mu越大，社团结构越模糊。为便于控制规模，本文设定网络参数如表1所示。

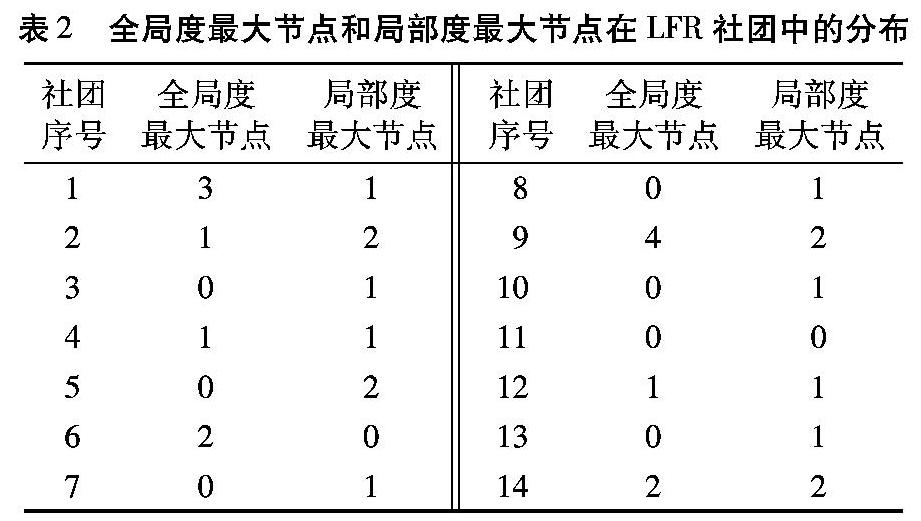
如表2所示，度值最大的14个全局度最大节点的分布并不均衡， 9号社团中分布了4个节点，而3、5、7、8、10、11、13号社团却无全局度最大节点； 反之，局部度最大节点的分布较为均衡，16个局部度最大节点均匀分布于12个社团中。进一步讲，对未知社团节点和数目的网络，通常无法确定应当选取多少个全局度最大节点作为种子节点。故局部度最大节点更适合作为网络社团划分的种子节点。

2 本文算法

2.1 算法描述

本文算法第一阶段为寻找网络局部度最大节点集合。第二阶段选取局部度最大点集中任意节点作为社团种子节点，开始社团扩展。首先选种子节点最大度值邻居节点组成初始社团，计算初始社团与邻居节点的亲密度值；然后选取亲密度大于0.5的邻居节点加入社团，若无符合此条件节点，选择亲密度最大节点，计算其加入社团后局部模块度的增加值是否为正，若为正则加入，否则判断下一亲密度次大节点，直至无邻居节点可使得模块度增长，局部社团划分结束，重复此过程，直至完成所有社团划分。第三阶段为社团合并。算法第二阶段运行完成后，会产生一些与其他社团高度重叠社团，此时执行社团合并。算法首先利用式（6）计算社团之间相似度，若存在两个社团的相似度Sim（ci，cj）>ε= 0.5，表示较小社团的大部分节点也存在于较大社团中，算法执行社团合并。若该条件未满足，ci和cj共有节点为社团重叠节点。

通过全局模块度划分社团结构会存在分辨率限制问题，不仅一些小规模的社团无法发现，而且可能错误划分大规模社团，原因在于全局模块度定义依赖于网络全局属性，本文算法以网络局部指标局部模块度确定社团结构从而避免了分辨率限制的问题。

2.2 时间复杂度

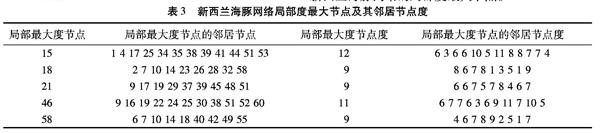
假定网络中节点个数为N，边为M，网络节点平均度D，T为平均社团规模，V为平均社团数量。在算法的第一阶段，计算所有局部度最大节点的时间复杂度为O（D×N）；在算法第二个阶段，从已知的局部度最大节点中任选一个作为起始节点发展社团，寻找社团每个节点邻居节点时间复杂度为O（T×D），然后通过集合运算的社团的邻居集合时间复杂度为O（T×1），计算社团与邻居节点亲密度并选择社团最优节点的时间复杂度为O（V×T×D），计算社团的局部模块度的时间复杂度为O（V×T）；在算法第三阶段，计算社团之间的相似度并执行社团合并，所花费时间复杂度O（V）。本文算法总的时间复杂度为O（D×N+T×D+T×1+ V×T×D +V×T+V），因D=2M/N，T=N/V，T

2.3 算法示例

本文以新西兰海豚网络作为算法演示数据集，依据式（1）寻找局部度最大节点，形成节点集P，表3第一列所示为新西兰海豚网络的局部度最大节点。

为分析种子节点选取顺序对于算法性能的影响，我们对算法进行二次测试。不同于上述任意选取种子节点为起始节点，以种子节点度值大小为优先选取依据。海豚网络的局部度最大节点集P中节点度从小到大为{18，21，58，46，15}，运行本文算法时选取的种子节点顺序为{18，21，58}，算法最终得到与上述任意选取种子为起始节点相同的划分结果，而节点46和15分别成为以节点58和21为种子的社团成员，可见本文算法有较好的稳定性，种子节点的选取顺序对算法结果无影响。

3 大规模真实网络实验

3.1 实验设定

为充分测试算法性能，将本文算法应用于斯坦福大学SNAP（Standford Network Analysis Project）项目中的大规模社团标准数据集。如表5所示，这些大规模的数据集的节点数目最多达到三百万，社团数表示网络的真实社团数目。数据集中一个顶点可以属于多个社团。

Amazon 该网络为亚马逊产品网络，其中顶点表示产品，若两款产品常被共同购买，它们之间会生成一条边。亚马逊提供产品类别定义表示网络的真实社团。

DBLP 该网络为计算机科学文献网络，提供了一个全面的计算机科学的研究论文列表，以此构建了一个论文合著关系网络。其中每个顶点表示一位作家，若两个作者共同写了一篇论文，则两个作者有边相连。作者所发表论文的期刊或会议表示网络的真实社团。

Ploblogs 该网络为美国政治博客网络。由Adamic和Glance在2005年记录的一个关于美国政治的博客网站的超链接组成的有向博客网络。由博客目录的说明或自我评价表明个体所属的真实社团，自由派或保守派。

Orkut 该网络为类似Youtube网络的社交网络，顶点表示社交网络用户，边表示用户之间的友谊关系。用户创建的群组表示网络的真实社团。

以上所有网络都转换为无向无权网络，各网络的详细情况如表5所示。

3.2 实验结果

图3和图4分别为测试的算法的F1Score指标和NMI指标。图中缺少的列表示该算法在对应数据集上的运行时间多于7天。因为算法复杂度之间的主要差别是在数量级上，单线程和多线程并不影响此点，故所有算法皆被设置为单线程运行状态。

在最大规模的3个数据集Amazon、DBLP和Orkut中，由于Amazon数据集拥有较高的社团内嵌度，5种算法在Amazon数据集社团划分效果都很好，而其余两个数据集的内嵌度都较低，相应的，5种算法F1Score指标和NMI指标都略低。

从图3、4可以看出，虽然存在偏差，F1Score指标和NMI指标总体是相关的。大体上来看，本文算法在两种指标衡量中表现最好，除了Orkut以外的3个测试数据集中性能最为稳定，在最大规模网络Orkut数据集中，本文算法运行效果也最为接近表现最好的Oslom算法。

图5显示了各种算法的执行时间，可以看出本文算法和Bgll算法明显优于其他算法，运行时间上相差至少一个数量级。由于Bigclam和Infomap算法分析Orkut数据集运行时间超过七天，故没有显示在图5中。本文算法和Infomap算法在较小规模网络Polblogs 中的运行时间一样少至几秒钟，而在其余三个网络中本文算法为最快，其次为Bgll算法。

图6和图7显示了在两组LFR数据集中运行各种算法的NMI指标。从图6中看出本文算法在mu<0.2时发现的社团数目较多，NMI指标明显高于其他三种算法。随着社团重叠节点数目增多，当mu>0.3时，本文算法的NMI指标缓慢下降。图7中LFR仿真网络R2规模为R1的10倍，四种算法在R2中性能表现普遍低于R1中。在两组仿真网络数据中Bigclam算法稳定性最弱，本文算法在社团结构较为清晰的情况下性能最优，社团结构模糊情况下性能略差于Oslom算法。

为比较各种算法的时间效率，本文再次生成了LFR仿真网络集R3，包含10个仿真网络， 网络规模由小到大（1000～10000），其他参数相同（k=20， maxk=50， minc=20， maxc=100，mu=0.1）。

图8所示为5种算法运行于10个LFR仿真网络的时间。可以看出，随着网络规模的扩大，各算法消耗时间越来越多。Bigclam算法运行效率较低，当节点数目达到10000时，运行时间比最好算法运行时间几乎多出一倍。5种算法在节点数目较少时（小于4000）运行时间相差不大，当节点数目大于5000时，本文算法和Bgll算法体现出较好的时间效率，直到网络规模达到10000节点时，运行时间仅仅不到40s。

5 结语

本文提出一个基于局部模块度改进社团划分算法，算法首次提出了社团与节点之间的亲密度的概念，以其作为新节点加入社团的衡量标准，以Clauset模块度增量作为局部社团终止指标，极大提高了社团划分的精度与速度。算法还提出以局部度最大节点作为社团种子节点，并以可控规模的LFR数据集网络实验分析了局部度最大节点在局部社团分布规律，证明其作为种子节点可行性和有效性。应用本文算法在大规模实际网络和人工仿真网络实验中，研究表明，本文算法比一些目前具有代表性的算法有更稳定的性能和更好的时间效率。

参考文献：

[1]DUCH J， ARENAS A. Community detection in complex networks using extremal optimization[J]. Physical Review E， 2005， 72（2）： 027104.

[2]FORTUNATO S. Community detection in graphs[J]. Physics Reports，2010， 486（3）： 75-174.

[3]李晓佳，张鹏，狄增如，等. 复杂网络中的社团结构[J]. 复杂系统复杂性科学，2008， 5（3）： 19-42.（LI X J， ZHANG P， DI Z R， et al. Community structure of complex networks[J]. Complex Systems and Complexity Science， 2008， 5（3）： 19-42.）

[4]LANCICHINETTI A， FORTUNATO S， KERTSZ J. Detecting the overlapping and hierarchical community structure in complex networks[J]. New Journal of Physics， 2009， 11（3）： 033015.

[5]汪小帆， 刘亚冰. 复杂网络中的社团结构算法综述 [J]. 电子科技大学学报， 2009， 38（5）： 537-543.（WANG X F， LI Y B. Overview of algorithms for detecting community structure in complex networks[J]. Journal of University of Electronic Science and Technology of China， 2009， 38（5）： 537-543.）

[6]刘旭，易东云.基于局部相似性的复杂网络社区发现方法[J].自动化学报，2011， 37（12）： 1520-1529. （LIU X， YI D Y. Complex network community detection by local similarity[J]. Acta Automatica Sinica， 2011， 37（12）： 1520-1529.）

[7]CLAUSET A. Finding local community structure in networks[J]. Physical Review E， 2005， 72（2）： 026132.

[8]LUO F， WANG J， PROMISLOW E. Exploring local community structures in large networks[J]. Web Intelligence and Agent Systems， 2008， 6（4）： 387-400.

[9]BAGROW J P. Evaluating local community methods in networks[J].Journal of Statistical Mechanics： Theory and Experiment， 2008， 2008（5）： P05001.

[10]CHEN M， KUZMIN K， SZYMANSKI B K. Extension of modularity density for overlapping community structure[C]// Proceedings of the 2014 IEEE/ACM International Conference on Social Networks Analysis and Mining. Piscataway， NJ： IEEE， 2014： 856-863.

[11]CHEN Q， FANG M. An efficient algorithm for community detection in complex networks[EB/OL].[2015-10-25].http：//140.123.102.14：8080/reportSys/file/paper/htchiang/htchiang_10_paper.pdf.

[12]REDNER S. How popular is your paper？ An empirical study of the citation distribution[J]. The European Physical Journal B-condensed Matter and Complex Systems， 1998， 4（2）： 131-134.

[13]CHEN Q， WU T T. A method for local community detection by finding maximaldegree nodes[C]// Proceedings of the 2010 International Conference on Machine Learning and Cybernetics. Piscataway， NJ： IEEE， 2010， 1： 8-13.

[14]BLONDEL V D， GUILLAUME J L， LAMBIOTTE R， et al. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics： Theory and Experiment， 2008， 30（2）： 155-168.

[15]ROSVALL M， BERGSTROM C T. Multilevel compression of random walks on networks reveals hierarchical organization in large integrated systems[J]. PloS One， 2011， 6（4）： e18209.

[16]YANG J， LESKOVEC J. Overlapping community detection at scale： a nonnegative matrix factorization approach[C]// Proceedings of the 6th ACM International Conference on Web Search and Data Mining. New York： ACM， 2013： 587-596.

[17]LANCICHINETTI A， RADICCHI F， RAMASCO J J， et al. Finding statistically significant communities in networks[J]. PloS One， 2011， 6（4）： e18961.

[18]袁超，柴毅. 复杂网络的局部社团结构挖掘算法[J].自动化学报，2014，40（5）：921-934.（YUAN C， CHAI Y. Method for local community mining in the complex networks[J]. Acta Automatica Sinica， 2014， 40（5）： 921-934.）