基于GPU图像去噪总变分对偶模型的并行计算

赵明超 陈智斌 文有为

摘要：研究基于总变分（TV）的图像去噪问题，针对中央处理器（CPU）计算速度较慢的问题，提出了在图像处理器（GPU）上并行计算的方法。考虑总变分最小问题的对偶模型，建立原始变量与对偶变量的关系，采用梯度投影算法求解对偶变量。数值实验分别在GPU与CPU上进行。实验结果表明，总变分去噪模型对偶算法在GPU设备上执行的效率高于在CPU上执行的效率，并且随着图像尺寸的增大，GPU并行计算的优势更加突出。

关键词：并行计算；总变分；图像去噪； 图像处理器

中图分类号：TN911.73 文献标志码：A

Abstract： The problem of Total Variation （TV）based image denoising was considered. Since the traditional serial computation speed based on Central Processing Unit （CPU） was low， a parallel computation based on Graphics Processing Unit （GPU） was proposed. The dual model of the total variationbased image denoising was derived and the relationship between the primal variable and the dual variable was considered. The projected gradient method was applied to solve the dual model. Numerical results obtained by CPU and GPU show that the algorithm implemented by GPU is more efficient than that by CPU， and with the increasing of image size， the advantage of GPU parallel computing is more outstanding.

Key words：parallel computation； Total Variation （TV）； denoising； Graphics Processing Unit （GPU）

0 引言

在物理成像系统以及传输过程中，图像常常被噪声污染而退化，从而造成视觉损伤，故图像去噪是图像处理过程中的一项重要操作。图像去噪经过几十年的研究，已取得重大成果，但它仍然是充满活力的领域[1]。随着科技的发展，图像尺寸持续增加，要求新算法提出的同时也需要计算硬件设备的更新。由过去单纯提高单核时钟频率来提升设备计算性能的技术达到瓶颈后，利用多核并行计算提升设备计算性能已成为研究的热点。

图像处理器（Graphics Processing Unit， GPU）是早期为实现图形实时渲染着色而开发的图形处理设备，它拥有众多计算核心和高带宽，因此具有很高的计算吞吐量[2]。实验表明，它是大规模并行计算得以实现的合适硬件设备。经过数十年的开发研究，一种基于统一计算设备单元（Compute Unified Device Architecture， CUDA）新架构构建的GPU可以方便地使用C语言的扩展语言实现并行化计算[3]。CUDA C一经面世，它便成为人们主要关注的对象。许多重要领域都积极研究开发基于GPU的应用程序，例如，模式识别、基因（DeoxyriboNucleic Acid，DNA）序列校对、计算流体力学、量子力学和环境科学等。随着CUDA技术的逐渐成熟，图像处理领域的研究者也正在积极地将其引入到该领域中，特别是医学图像TechniScan的基于CUDA架构的超声波成像系统，使得医生可在20min内获得患者高清三维图像。

在图像处理过程中，一幅灰度图像可以对应一个二维矩阵或一个列向量，列向量是由二维矩阵转化来的。由Rudin，Osher和Fatemi提出的总变分去噪模型（RudinOsherFatemi， ROF）[4]，可以高效去除图像噪声，保留图像的边缘信息。ROF模型是根据式（1）得出：

近年来，研究者提出了许多关于总变分模型的算法，例如原对偶算法[6]、对偶算法[7-8]和Chambolle 算法[9]。这些算法包含相当的计算量，随着图片像素的不断提高以及图片尺寸的增大，给实时图像处理带来巨大的挑战。尽管GPU的新架构CUDA可以实现并行计算，但并不是所有的算法可以不加更改地进行并行计算。一个好的并行算法，可以将费时的计算划分为一系列独立的统一操作的计算，同时需要考虑数据之间的切换，因为GPU的存储空间有限，数据间的交换同样会花费大量的时间，那么在设计并行计算时，需要尽可能地将数据传输降到最低。

随着总变分模型应用于不同的图像恢复任务，该模型也在不断变换，以适应新的环境，如文献[8，10]。而在文献[11]中，研究的是在GPU上实现TVL1正则模型的原始与对偶方法；文献[12]探究了TV模型在医学领域核磁共振图像去噪的应用，并且提出了解决TV正则化参数估计问题的方法。本文主要研究TVL2正则模型对偶算法的并行计算问题，将其在GPU的CUDA架构上实现，并与TVL2正则化模型对偶算法在CPU上的执行进行对比。

2 GPU实现

对偶算法是在GPU的新架构CUDA上实现的。在CUDA上运行的函数称为Kernel（内核函数）。Kernel以线程网格的形式组织，每个线程网格由若干个块组成，每个线程块又由若干线程组成。对于给定型号的GPU，一个块中可开辟最大线程数量是固定的。CUDA将计算任务映射为大量可以并行执行的程序，并由硬件动态调度和执行这些线程。只要声明了执行参数（设备的限制内），GPU设备会自动将数据分配到相应的处理单元上。

图像去噪空间差分算子和它的转置以及离散偏差运算都是主要的耗时运算操作。本文将在GPU上开启n个线程同时进行运算，每一个线程返回一个单精度的结果。当进行空间操作时，如空间差分第（i， j）个位置进行运算时需要用到它相邻位置的数据，不同块线程之间不能进行数据共享，故此处应用了GPU的缓存技术[2]。

当算法操作执行一个数据集的归约运算[2]，如对偶投影的计算，需要谨慎处理这样的操作，因为程序写得不当可能使运算时间加倍或者产生线程访问数据冲突。在这样的运算中，应将数据先分成大小合适的块，每个块执行部分数据求和，然后再将块中部分数据和再求和，使得GPU处理器众核得到高效利用。当进行分配块时，需要考虑数据传输的带宽限制和GPU本身资源的限制如寄存器、内存等。

本文算法在实现一个全局求和的过程中，每个块有256个线程，每个线程读取全局内存中的1个数据，然后将它们放到一个大小16×16的共享内存块中。每个块执行相同加和操作7次，然后将块中的256个线程中的数据再求和放到事先开辟的部分和全局向量（n2/2048）内存中，这样每个块可以执行2048个数据求和，最后将部分和全局向量内存中的数据求和即可完成本次操作。

在执行不依赖彼此的运行过程中，本文用到了GPU并行计算当中的流处理[15]。每个流是CUDA当中的一个同步单元。一个同步点可以定义多个由CUDA函数cudaThreadSynchronize（）控制的流。使用流，可以同时更新对偶变量，因为不同行的更新是独立的。

3 数值结果

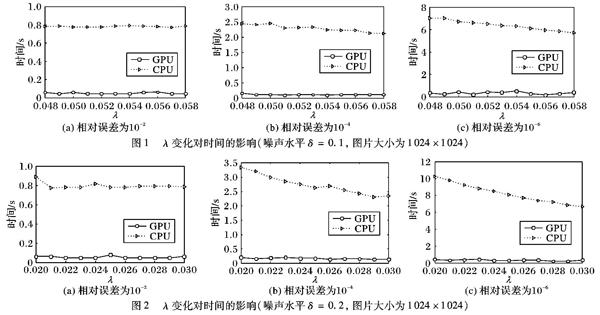
理论上，在GPU和CPU上执行的代码迭代次数（Iterations，Iter）应该是相同的，但是当达到一定精度后，就会出现迭代次数的差异，这是由于硬件的限制，算法在CPU上执行的数值运算是双精度，而在GPU上执行的是单精度。图1～2中也反映出，随λ的取值变化，算法在GPU上与CPU上的执行时间的变化不一致。因为在GPU上执行时精度比较低，因此它对参数变化的灵敏度比较低，而在CPU上执行时精度比较高，故它对参数变化的灵敏度较高，所以在CPU上执行算法时时间随参数的变化比较明显。

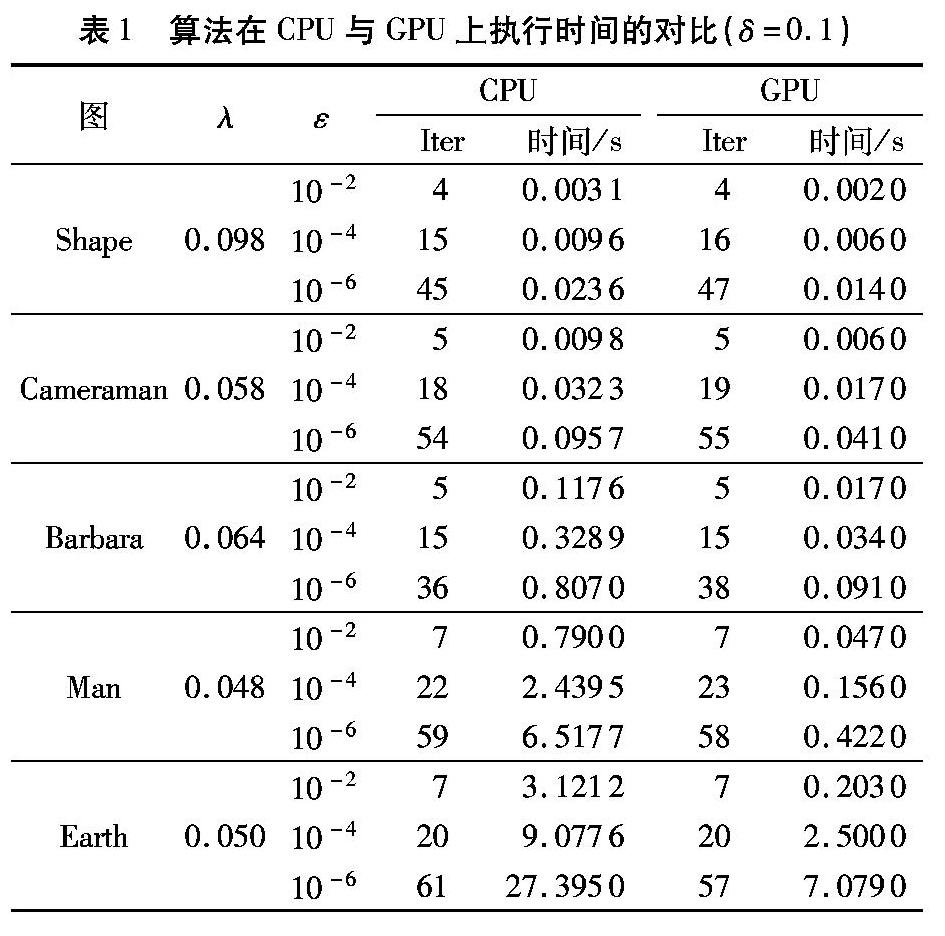
由于λ的取值也影响着算法迭代的时间，为了方便在不同设备上运行的时间进行对比，那么λ的取值尽量使得在GPU与CPU上运行迭代次数相同或差异控制在5%以内。表1实验结果表明，上述算法在GPU设备上执行的效率高于在CPU上，并且随着计算规模的增加，GPU加速效果更加明显。

4 结语

本文借助GPU计算设备，实现总变分图像去噪对偶算法的并行计算，解决总变分模型在实时图像处理时计算量大、耗时较长的问题。本文仅研究了灰度图像的并行计算，可以更进一步探究彩色图像的并行计算。在应用总变分图像去噪时没有考虑模型中参数选择的问题，参数选择在图像处理中是一个难点和热点问题。GPU并行计算并不仅限于图像处理这一领域，它主要针对具有计算规模大，耗时且实时性要求高的问题，对于这样的问题，都可以在GPU设备上进行并行计算研究。

参考文献：

[1]CHATTERJEE P， MILANFAR P. Is denoising dead？[J]. IEEE Transactions on Image Processing， 2010， 19（4）： 895-911.

[2]张舒， 褚艳利. GPU高性能运算之CUDA[M]. 北京：中国水利水电出版社，2009：5-13，141-189.（ZHANG S， CHU Y L. CUDA High Performance Computing GPU[M]. Beijing： China Water & Power Press， 2009： 5-13，141-189.）

[3]SANDERS J， KANDROT E. GPU高性能编程CUDA实战[M]. 聂学军，译. 北京： 机械工业出版社， 2011： 3-8. （SANDERS J， KANDROT E. CUDA by Example： an Introduction to GeneralPurpose GPU Programming[M]. NIE X J， translated. Beijing： China Machine Press， 2011： 3-8.）

[4]RUDIN L， OSHER S， FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica D： Nonlinear Phnomena， 1992， 60（1）： 259-268.

[5]CHAMBOLLE A， LIONS P L. Image recovery via total variation minimization and related problem[J]. Numerische Mathematik， 1997， 76（2）： 167-188.

[6]CHAN T F， GOLUB G H， MULET P. A nonlinear primaldual method for total variation based image restoration[J]. SIAM Journal on Scientific Computing， 1996， 20（6）： 1964-1997.

[7]CARTER J L. Dual methods for total variationbased image restoration[D]. Los Angeles： University of California， 2001： 8-41.

[8]ZHU M， WRIGHT S J， CHAN T F. Dualitybased algorithms for total variation image restoration[J].Computational Optimization and Applications， 2010， 47（3）： 377-400.

[9]CHAMBOLLE A. An algorithm for total variation minimization and applications[J]. Journal of Mathematical Imaging and Vision， 2004， 20（1/2）： 89-97.

[10]CHAN T F， ESEDOGLU S， PARK F， et al. Total Variation Image Restoration： Overview and Recent Developments[M]. New York： Springer US， 2006： 17-31.

[11]POCK T， UNGER M， CREMERS D， et al. Fast and exact solution of total variation models on the GPU[C]// Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops. Washington， DC： IEEE Computer Society， 2008： 1-8.

[12]LIU L R， SHI L， HUANG W H， et al. Generalized total variationbased MRI Rician denoising model with spatially adaptive regularization parameters[J]. Magnetic Resonance Imaging， 2014， 32（6）： 702 -720.

[13]BOYD S， VANDENBERGHE L.凸优化[M].王书宁，许鋆， 黄晓霖，译. 北京：清华大学出版社， 2013： 85-89.（BOYD S， VANDENBERGHE L. Convex Optimization[M].WANG S N， XU Y， HUANG X L， translated. Beijing： Tsinghua University Press， 2013： 85-89.）

[14]BERTSEKAS D P. Nonlinear Programming[M]. 2nd ed. Nashua： Athena Scientific， 1999： 9.

[15]KIRK D B， HWU W M.大规模并行处理器编程实战[M].陈曙晖， 熊淑华，译. 北京：清华大学出版社，2010：65-78.（KIRK D B， HWU W M. Programming Massively Parallel Processors： a Handson Approach[M]. CHEN S H， XIONG S H， translated. Beijing： Tsinghua University Press， 2010：65-78.）

[16]DERIN B S， RAFAEL M， KATSAGGELOS A K. Parameter estimation in TV image restoration using variational distribution approximation[J].IEEE Transactions on Image Processing，2008，17（3）：326-339.