分步的基于模糊聚类的多雷达航迹关联算法

张树斌 方洋旺 雍霄驹 彭维仕 李伟

摘要：针对采用传递闭包模糊聚类的多雷达航迹关联算法运算量较大的问题，提出了分步的基于模糊聚类的多雷达航迹关联算法。首先基于欧氏距离对航迹进行预关联判断，然后通过模糊相似计算，简化了航迹相似矩阵，进而减少了相似计算与矩阵迭代的次数，最终达到了减小运算量的目的。仿真结果表明：所提算法在保证关联正确率的前提下，耗时减小了54%，有效地提高了多雷达航迹关联算法的效率。

关键词：信息融合；分步；目标跟踪；航迹关联；模糊聚类

中图分类号：TP274 文献标志码：A

Abstract： Since the multiradar track correlation algorithm based on transitive closure fuzzy clustering has high computational complexity， a stepbystep multiradar track correlation algorithm based on fuzzy clustering was proposed. First， based on the Euclidean distance the track correlation was judged， and the track similar matrix was simplified through fuzzy similarity calculation. Furthermore， the calculation of the iterations was decreased. Finally， the computational demanding of the proposed algorithm was certainly reduced. The simulation results show that the proposed algorithm can determine targets tracks accurately， saves 54% of time effectively with the high accuracy.

Key words：information fusion； stepbystep； target tracking； track correlation； fuzzy clustering

0 引言

现代战争中，传统的单雷达对目标的探测难以满足作战要求，必须运用多部雷达，多方位、多角度地对目标进行探测。因此，多雷达航迹融合是现代化战争的需要。在分布式多雷达的环境下，各雷达独立观测目标，得到大量目标的重复航迹信息。然而，航迹与航迹关联（或互联）问题就是判断不同系统的航迹是否代表同一个目标，以获取目标的正确信息[1]。

航迹关联是多雷达数据融合的一个关键问题，也是实现多雷达航迹数据合成的前提，关联判定结果将直接影响到整个融合系统的性能[2]。现有的主要方法有拓扑序列的方法[3-5]、灰色理论的方法[6]和神经网络的方法[7]。拓扑序列方法虽然具有很高的关联成功率，但进行一次完整匹配过程的计算量很大，不适合大数量目标的航迹关联[8]；灰色理论虽然对样本量要求不高，但航迹关联判定准则是局部最优的[6]；神经网络虽然运算量较小，但对参数选择要求较高[7]。而传统的航迹关联算法主要是基于统计学[9-10]和模糊数学的方法[1，11-14]。基于统计学的方法不能有效获得精确的目标航迹信息，当存在较大的误差干扰时，其航迹关联性能被削弱。针对上述问题，基于模糊数学的方法能有效解决实际关联过程中的模糊性。其中，采用传递闭包模糊聚类的多雷达航迹关联算法[15]为典型的基于模糊数学的航迹关联算法，面对目标密集、做机动的情况也能准确地进行关联判定，但当目标数量较大时，其运算量增大，很难将其应用到工程实践中[16]。因此本文主要针对该算法存在的不足，提出了分步的基于模糊聚类的多雷达航迹关联算法。首先利用欧氏距离对航迹进行预关联判断，然后通过模糊相似计算，简化航迹相似矩阵，进而减少相似计算与矩阵迭代的次数，以期达到减小运算量的目的。

1 问题描述

假设两部雷达对同一空域的目标进行探测，且认为同一雷达的不同航迹是不关联的。设两部雷达测得的航迹集合分别为：

其中：n1为雷达1测得的航迹数，n2为雷达2测得的航迹数；x1jk表示雷达1测得航迹中第j条航迹的第k个航迹信息，x2jk表示雷达2测得航迹中第j条航迹的第k个航迹信息。航迹信息可以为目标的位置、速度、加速度及其他在航迹关联中起作用的目标信息。

传递闭包模糊聚类的多雷达航迹算法以航迹信息为模糊因子计算不同航迹的相似系数r构成相似矩阵，而后求得模糊等价矩阵R，最终实现关联判定。算法的核心是计算模糊等价矩阵，虽然关联准确性较高，然而当目标数量增大时求解等价矩阵的运算量非常大。其原因主要是：1）等价矩阵的维数与目标数量有关；2）求解等价矩阵的迭代次数与矩阵维数有关。因此，算法面对大量目标时不能及时进行关联判定。

9）比较航迹关联性，找出航迹关联对。

①找出Rλ21中的最大值元素，并假设最大值元素在第i行第j列，则雷达1的第i条航迹与雷达2的第j条航迹为同一目标的航迹，建立航迹关联对；

②假设同一个雷达的不同航迹互不关联，故同一雷达的不同航迹为不同的目标，且航迹间的关联系数应为零。所以将Rλ21的第 i行和第j列的所有元素改为零；如果Rλ21中存在非零元素，则表示判断未结束，继续重复①～②，直至Rλ21中所有元素为零，此时结束关联判断。

3 仿真分析

下面将通过数值仿真验证新算法的有效性。假定两部雷达探测同一空域中的20个目标，分别采用新算法和原算法对其进行航迹关联，比较两种算法在相同的空域环境中算法的关联正确率及运算时间，验证本文算法能否在保证正确率的前提下减小运算时间，然后改变目标关联门限值进行多次仿真实验，分析其对正确关联率的影响。

3.1 目标运动模型

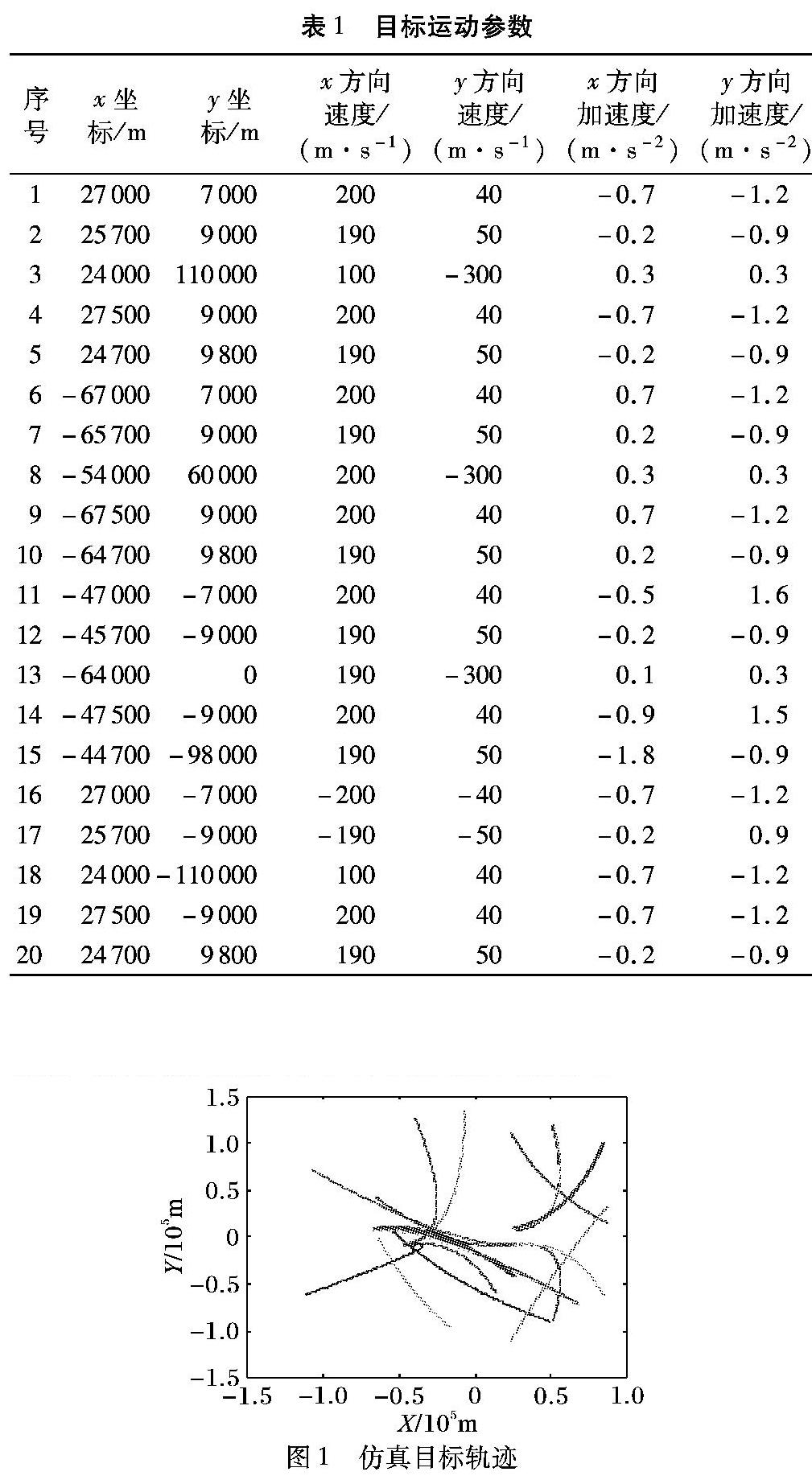
设目标的x坐标、y坐标、x方向速度、y方向速度、x方向加速度和y方向加速度为模糊因子。20个目标的初始运动参数如表1所示。

3.2 仿真验证

这里只考虑不同雷达的航迹关联问题，不考虑同一雷达对不同目标的航迹关联问题，并假设同一雷达的不同目标的航迹互不关联。设有两部雷达，以信息融合中心为坐标原点，采用直角坐标系，雷达坐标分别为（50000， 0）与（0， 0），单位为m，同时跟踪空域中的20个目标，探测周期均为2s，探测时长为400s，忽略系统误差。假定雷达1的距离测量误差为100m，角度误差为0.15°；雷达2的距离测量误差为50m，角度误差为0.1°。融合中心对航迹信息进行融合并判断航迹关联性。

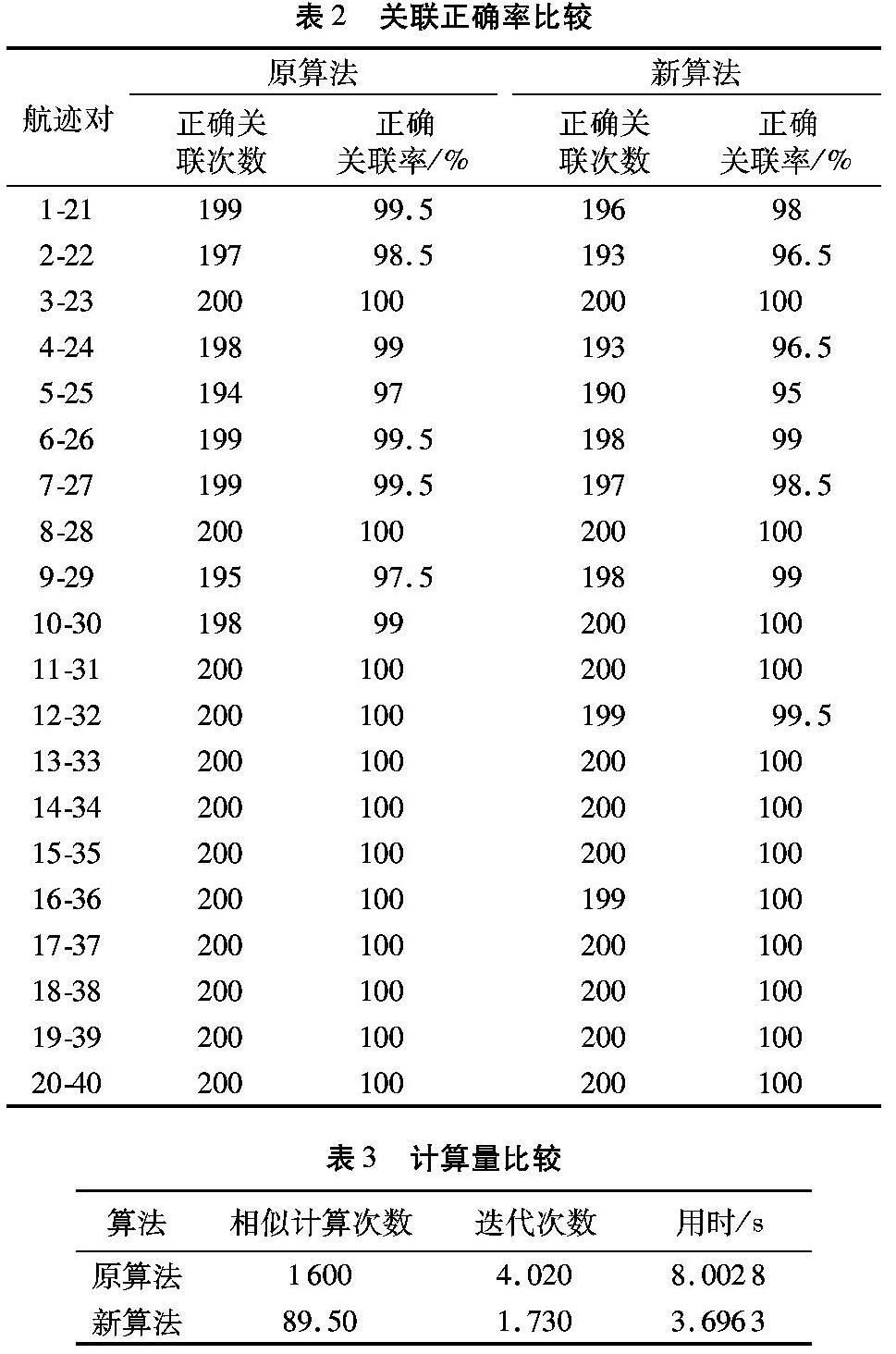
仿真一 将目标分类门限设为，分别采用原算法与本文所提算法进行100次蒙特卡罗仿真，比较仿真的平均正确关联率、平均用时，以及平均每个探测周期内的相似计算次数和模糊等价矩阵的迭代次数，结果如表2所示。

分析仿真结果，新算法较原算法运算量大为减少，相同条件下运算时间节约了54%（1-（3.6963/8.0028）），且保持了相当的准确率。

分析仿真结果，新算法较旧算法平均每次探测周期内相似计算次数由1600减少到89.5，且求解模糊等价矩阵的平均迭代次数由4.020减少到1.730，运算量大为减少，再者两种方法用时之比为：

相同仿真条件下运算时间从8.0028s提高到3.6963s，节约了54%的运算时间，且准确率相当。

仿真二 改变目标分类门限θ的值，分别进行100次的蒙特卡洛仿真，比较不同θ时20个航迹对的平均正确关联率及运算时间。仿真结果如图2、3所示。从图2可知，θ≥0.01时，正确关联率较高；θ<0.01时，正确关联率降低，分析原因为：门限过小造成不同雷达由同一目标得到的不同航迹间欧氏距离大于门限值，直接判断为不关联，导致了漏相关的发生，降低了正确关联率。从图3可知，θ越小，运算时间越短，分析原因为：较小的门限使得预判断效率提高，相似矩阵更为简化，运算量得以减少。实际中要综合考虑正确关联率与实时性的要求，选择合适的门限值以满足航迹关联的需求。

4 结语

本文提出了分步的基于模糊聚类的多雷达航迹关联算法，解决了采用传递闭包模糊聚类的多雷达航迹关联算法运算量较大的问题。该算法基于航迹间的欧氏距离对航迹进行预关联判断，通过简化航迹相似矩阵，减少相似计算以及矩阵迭代的次数，达到了减少运算量的目的。仿真结果表明：选择合适的目标分类门限，分步的基于模糊聚类的多雷达航迹关联算法在保证关联正确率的前提下，耗时减小了54%，有效提高了多雷达航迹关联算法的效率。

参考文献：

[1]何友，王国宏，陆大硷， 等.多传感器信息融合及应用[M].北京：电子工业出版社，2000： 114-115.（HE Y， WANG G H， LU D J， et al. Multisensor Information Fusion with Application[M]. Beijing： Publishing House of Electronics Industry， 2000： 114-115.）

[2]韩崇昭，朱洪艳，段战胜，等.多源信息融合[M].北京：清华大学出版社，2006： 290-291.（HAN C Z， ZHU H Y， DUAN Z S， et al. Multi Source Information Fusion[M]. Beijing： Tsinghua University Press， 2006： 290-291.）

[3]吴泽明，任姝婕，刘熹.基于拓扑序列的航迹关联算法研究[J]. 航空学报，2009，30（10）：1937-1942.（WU Z M， REN S J， LIU X. Topology sequence based track correlation algorithm[J].Acta Aeronautica ET Astronautica Sinica， 2009，30（10）：1937-1942.）

[4]WU Z M. A novel track correlation algorithm for radar data fusion[C]// Proceedings of the 7th International Conference on Wireless Communications， Networking and Mobile Computing. Piscataway， NJ： IEEE，2011：1-4.

[5]董凯，王海鹏，刘瑜.基于拓扑统计距离的航迹抗差关联算法[J].电子与信息学报，2015，37（1）： 50-55.（DONG K， WANG H P， LIU Y. Antibias track association algorithm based on topology statistical distance[J]. Journal of Electronics & Information Technology， 2015，37（1）： 50-55.）

[6]董凯，关欣，王海鹏，等.基于序贯修正灰关联度的全局最优航迹关联算法[J].电子与信息学报， 2014， 36（8）： 1940-1945.（DONG K， GUAN X， WANG H P， et al. Global optimal track association algorithm based on sequential modified grey association degree[J].Journal of Electronics & Information Technology，2014，36（8）：1940-1945.）

[7]DUAN M， LIU J H. Track correlation algorithm based on neural network[C]// Proceedings of the 2009 2nd International Symposium on Computational Intelligence and Design.Washington， DC： IEEE Computer Society， 2009： 181-185.

[8]吴泽明，蒋叶金，任姝婕.拓扑序列航迹关联的高效修正算法[J]. 西安电子科技大学学报，2011，38（2）：180-186.（WU Z M， JIANG Y J， REN S J. Effectively modified topology sequence track correlation algorithm[J]. Journal of Xidian University， 2009， 35（6）： 986-991.）

[9]SINGER R A，KANYUCK A J. Computer control of multiplesite track correlation[J]. Automation， 1971，7（3）：455-463.

[10]BARSHALOM Y. On the sequential track correlation algorithm in multisensor data fusion system[J]. IEEE Transactions on Aerospace and Electronic Systems，2008，44（1）： 396-396.

[11]李亮群，姬红兵.基于最大熵模糊聚类的快速数据关联算法[J]. 西安电子科技大学学报（自然科学版），2006，33（2）：251-256. （LI L Q， JI H B. Fast data association algorithm based on maximum entropy fuzzy clustering[J]. Journal of Xidian University （Natual Science）， 2006，33（2）： 251-256.）

[12]ZHANG G， LIU Y， SHAN K F. An improvement of track correlation for distributed fusion system[J].International Journal of Digital Content Technology and Its Applications，2012，6（14）：306-313.

[13]范恩，谢维信，刘宗香. 基于子航迹Hough变换的模糊航迹关联[J]. 深圳大学学报（理工版），2013，30（6）：551-556.（FAN E， XIE W X， LIU Z X. Fuzzy track association using trackletbased Hough transform[J].Journal of Shenzhen University （Science & Engineering）， 2013，30（6）： 551-556.）

[14]HUANG Y， LI L， ZHOU Y. A heterogeneous sensors tracktotrack correlation algorithm based on fuzzy numbers similarity degree[C]// Proceedings of the 2nd International Conference on Information and Computing Science. Piscataway， NJ： IEEE， 2009： 191-194.

[15]黄友澎. 多传感器多目标航迹关联与数据合成若干关键技术研究[D]. 哈尔滨：哈尔滨工程大学， 2009： 33-40.（HUANG Y P. Research on several key techniques of multisensor multitarget track correlation and data combination[D]. Harbin： Harbin Engineering University， 2009： 33-40.）

[16]BAI J，WANG G H，KONG M.A regional track correlation method for multiradar multitrack in distributed radar network[C]// CIE 2006： International Conference on Radar. Piscataway， NJ： IEEE， 2006： 1-3.