物流园区空间吸引的劳动力转移与产业集聚

王勇　刘永　龚科

摘要：针对我国当前农村劳动力在地域间大规模转移与产业集聚水平差距的扩大，本文通过构建基于物流园区空间吸引的引力模型明确引力模型中的“质量”与劳动力转移率的关系，结合中西部地区的城乡“二元结构”形态构建了劳动力转移和产业集聚模型，从物流园区空间吸引的视角分析劳动力转移与产业集聚效应，通过模型仿真分析运输成本、劳动力转移率、劳动力产品收益间接效用函数幂指数、不同地区间制造业产品产出比关系，发现物流园区空间吸引力与劳动力转移率之间具有正的相关性，运输成本与产业集聚效应之间具有负的相关性，而劳动力转移率对产业集聚效应和劳动力产品收益具有规模报酬递增的特征。

关键词：物流园区；空间吸引；劳动力转移；产业集聚；二元结构

中图分类号：F0615文献标识码：A

随着我国经济的发展和区域物流业发展的不断增强，物流园区空间吸引范围不断外延，地区间收入差距持续扩大，劳动力转移和产业集聚现象逐渐凸显。区域物流的发展、特别是物流园区的建设促进了区域产业结构的转变，增强了区域经济竞争力，但也呈现出因地区经济差异而导致的物流园区分布构建不合理的现象，区域间缺乏有效的协调制约了区域内生产要素的流通，而物流园区的空间吸引是造成地区劳动力转移和产业集聚的主要影响因素之一。针对我国中西部地区城乡“二元结构”的经济形态，本文拟从物流园区空间吸引的角度分析劳动力转移和产业集聚的特征，试图分析劳动力在地域间的转移问题和产业集聚效应的形成特点，并试图验证劳动力转移率对产业集聚和劳动力产品收益具有正向规模报酬递增作用。

一、基于物流园区空间吸引的劳动力转移和产业集聚模型

（一） 变量定义

假定存在两个地区（地区1和地区2）具有对称的经济结构，也即地区1和地区2具有相似的生产函数类型。本文以上述两地区为研究对象，下面介绍涉及到的一些定义和符号。

定义1：地区1和地区2均有城市、乡镇和农村，且地区1和地区2具有V、L和H三种生产要素，其中V为可耕种的土地，L为低技能劳动力，H为高技能劳动力，高技能劳动力可以在不同的地区之间不受限制转移，而低技能劳动力的转移受到条件限制。

定义2 ：D{Duu=1，2，…，m′}为参与评价的专家数；U{Ui，t|i=1，2；t=1，2，…，r}为地区i的评价指标属性；

Xi，u，t，l（i=1，2；u=1，2，…，m′；t=1，2，…，r；l=1，2，…，ν）为专家u对于地区i的指标因素t下的实物l的综合评价值，用模糊数表示为Xi，u，t，l=（ai，u，t，l，bi，u，t，l，ci，u，t，l），W{Wi，u，t|i=1，2；u=1，2，…，m′；t=1，2，…，r}为专家u对地区i的指标因素t的评价值，并用模糊数表示为Wi，u，t=（hi，u，t，vi，u，t，si，u，t），也被称作模糊属性权重，Zi，l为多位专家对地区i的实物l的综合评价值，用模糊数表示为：Zi，l=（Ti，l，Oi，l，Hi，l），ωi，l为Zi，l的集成指标函数值，τ为劳动力转移率的阻尼系数。

定义3：地区1和地区2的三种生产要素归属于农村部门、乡镇企业部门、物流生产制造业部门和物流服务业部门，其中F为农村部门生产的产品，E为乡镇企业生产的产品，Q为物流生产制造业部门的产品，S为物流服务业部门生产的产品，且F型产品和E型产品来自农村和乡镇，Q型产品和S型产品来自城市。

定义4： d{di|i=1，2}表示地区i的运输成本，而1/di表示地区i的运输产品的到达率，运输成本越小越容易到达目的地，运输产品的价格也就越低，产品的收益也就越高。因此，劳动力转移和产业集聚与运输成本密切相关。

定义5 ：F{Fi|i=1，2}表示地区i的F型产品的产出，LFi表示地区i利用的低技能劳动力的数量，Ci表示地区i的可耕种土地面积。

定义6 ：E{Ei|i=1，2}表示地区i的E型产品的数量，Q{Qi|i=1，2}表示地区i的Q型产品的数量，S{Si|i=1，2}表示地区i的S型产品的数量，LEi表示地区i的E型产品雇佣的劳动力数量，LSi表示地区i的S型产品生产部门雇佣的劳动力数量，LSi0表示地区i的城市低技能劳动力初始数量，ΔLSi表示地区i的低技能劳动力潜在转移量。由于低技能劳动力转移受到城市相关条件限制而导致仅有一定比例的劳动力可以从农村和乡镇转移到城市，设定λi表示地区i基于低技能劳动力潜在转移量的转移率（0λi1）。

定义 7： PFi表示地区i的F型产品价格，PEi表示地区i的E型产品价格，PQi表示地区i的Q型产品价格，PSi表示地区i的S型产品价格，wi表示地区i的劳动力产品收益，ei表示地区i的低技能劳动力与劳动力产品收益间接效用函数的幂指数。

定义 8 ：Qi，j表示地区i的第j种Q型产品的生产数量，Ni表示地区i的Q型产品的种类，f表示用于Q型产品生产的固定投入，c表示Q型产品生产的边际投入，gi，j表示地区i的第j种Q型厂商所雇佣的高技能劳动力数量。

定义 9 ：γ表示F型产品生产函数的弹性系数，ζ表示E型产品的生产相关系数，ψi表示地区i劳动力潜在转移量与劳动力产品收益的相关系数，φ表示不同种类的Q型产品生产函数的替代弹性系数，σ和β表示S型产品生产函数的弹性系数。

（二）基于物流园区空间吸引的引力模型

物流园区的空间吸引可产生一定的辐射力，并促进城市在发展过程中逐渐吸引劳动力转移和产业集聚[1-2]。物流园区的空间吸引力与其对周围地区的吸引强度成正比，与区域之间的距离成反比。引力模型是用于预测和分析事物空间相互作用形式的数学模型[3-5]，常用于分析区域间的信息流、货物流和人员流动等。本文利用引力模型原理计算城市物流园区的引力大小，构建劳动力转移概率模型，进而构建劳动力转移和产业集聚模型。

假设在地区1和地区2的城市均有物流园区，而农村和城镇可看做一个整体，简称农镇，其没有物流园区但拥有可耕种的土地和大量低技能劳动力，物流园区所在地区i的城市“质量”可表示为mi1，此处的mi1表示为地区i拥有物流园区的城市的整体经济实力，而地区i的农镇的质量可表示为mi2，此处的mi2表示为地区i的农村和城镇的经济基础，经济实力和经济基础主要是由交通便利程度、经济社会发展环境、地理区位条件和服务水平等因素共同组成。若地区i的城市与农镇的中间地带有j点（j∈J），其质量可表示为mij，其中J表示为城市和农镇之间辐射范围的边界线，则地区i的城市和农镇对j点的吸引力分别为：

Fi1j=kimi1mijli1j2Fi2j=kimi2mijli2j2（1）

式中Fi1j，Fi2j表示为地区i的城市和农镇对j点的吸引力，li1j，li2j表示为地区i的城市和农镇到j点的距离，ki为系数。将地区i的城市和农镇看作两点，它们的连线为x轴，两点之间的直线距离设为2a，两点连线的垂直平分线作y轴，交点O取为原点，设j点的坐标为（x，y），则有：

Fi1j=Fi2jmi1li1j2=mi2li2j2（2）

由上式计算得到：

mi1（（x-a）2+y2）=mi2（（x+a）2+y2）（3）

进一步变形得到：

（x+mi1+mi2mi2-mi1a）2+y2=[（mi1+mi2mi2-mi1）2-1]2 （4）

由上式可知j点轨迹是一个以（-mi1+mi2mi2-mi1a，0）为圆心，以2ami1mi2|mi2-mi1|为半径的圆。亦即质量大的实体点具有较强的空间吸引力，而质量小的实体点则具有较弱的空间吸引力。

（三）引力模型中“质量”及劳动力转移率的确定

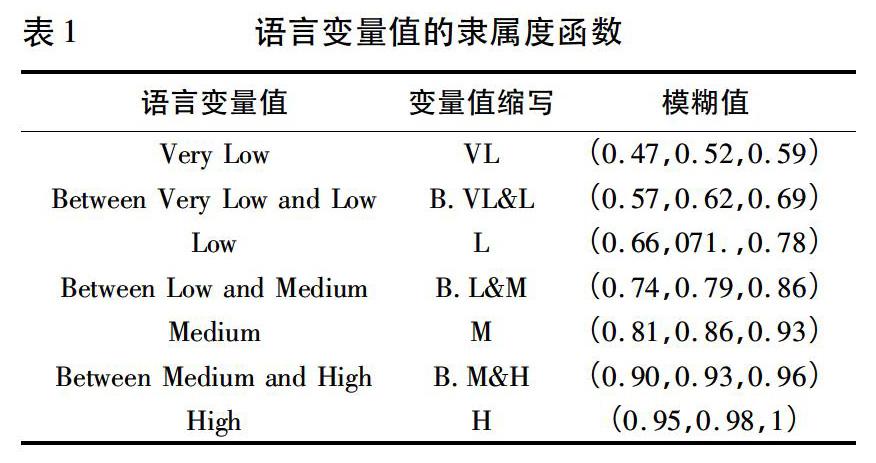
基于引力模型的分析需要确定地区i的城市质量mi1值和农镇质量mi2值，本文采用模糊综合评价方法[6-8]，从交通便利程度（U1）、经济社会发展环境（U2）、地理区位条件（U3）、服务水平（U4），物流供求状况（U5）和信息化程度（U6）等指标进行综合评价。基于上述综合评价指标将三角模糊数和语言变量相结合（见表1），对不同指标下城市和农镇的满意度及不同指标选择的满意度进行综合评价。

对上述6个指标进行评价时，语言变量值中的Low被Poor代替，Medium被Fair代替，High被Good代替，表1中的变量缩写值也作相应改变，对应的模糊数值不变。

由定义2可知Xi，u，t，l=（ai，u，t，l，bi，u，t，l，ci，u，t，l），Wi，u，t=（hi，u，t，vi，u，t，si，u，t），则多位专家对于地区i的实物l在指标因素t上的综合评价值可表示为：

Zi，l=1m′×r∑m′u=1（（Xi，u，1，lWi，u，1）（Xi，u，2，lWi，u，2）…（Xi，u，r，lWi，u，r））（5）

式中表示向量乘积，表示为向量加和，Zi，t，l表示多位专家对地区i的实物l在指标因素t上的综合评价值，m′表示总的专家数，r表示为总的评价指标数。

假定R=（b，u，e）表示一个三角模糊数，这三角模糊数的集成表示为：P（R）=14（b+2u+e）[6，9]。因此，由定义2可知Zi，l的三角模糊数表示为Zi，l=（Ti，l，Oi，l，Hi，l），则Zi，l的集成指标函数值ωi，l可以表示为：

ωi，l=14（Ti，l+2Oi，l+Hi，l）（6）

上式中求得的ωi，l即可对应表示地区i的城市“质量”mi1和地区i的农镇“质量”mi2，进而用于引力模型的计算。本文以城市和农镇两点的连线与轨迹圆的交点j以及阻尼系数τ来确定劳动力转移率，地区i的劳动力转移率的计算公式可以表示为：

λi=τi（mi1mi1-mi2-mi1mi2|mi2-mi1|）（7）

（四） 劳动力转移和产业集聚模型构建

基于物流园区空间吸引的劳动力转移和产业集聚模型，包含农村部门、乡镇企业部门、城市的物流生产制造业部门和物流服务业部门等的生产函数模型，且生产函数模型间相互关联和制约[1，3，10]，生产函数模型依次被介绍如下：

1.农村部门的生产函数模型

农村部门利用土地和低技能劳动力生产F型产品，地区i的F型产品数量的生产函数模型为：

Fi=L1-γFiCγi（8）

其中地区i的F型产品数量是由地区i利用的低技能劳动力数量和地区i的可耕种土地面积与弹性系数结合组成的函数式。

2.乡镇企业部门的生产函数模型

乡镇企业生产E型产品，假定E型产品的生产函数要素只是低技能劳动，则地区i的E型产品数量的生产函数模型为：

Ei=ζLEi（9）

其中地区i的E型产品数量是由地区i的E型产品雇佣的劳动力数量与生产相关系数ζ的乘积组成。

3. 劳动力产品收益的生产函数模型

假定不同地区的劳动力产品收益是与F型产品数量，S型产品数量，劳动力转移率，运输成本等相关的生产函数，则地区i的劳动力产品收益生产函数模型为：

wi=（PQidi）Si2-λiPFiFi2（10）

其中劳动力产品收益的生产函数模型是F型产品数量和S型产品数量的二元二次函数关系式。

4.城市低技能劳动力数量的生产函数模型

由于受到物流园区空间吸引的影响，部分低技能劳动力将从农村和乡镇转移到城市，劳动力转移率是导致城市低技能劳动力数量变化的主要影响因素，因此地区i的城市低技能劳动力数量的生产函数模型为：

LSi=LSi0+λiΔLSi（11）

其中城市低技能劳动力数量由初始城市低技能劳动力数量和低技能劳动力转移量共同组成，城市和农村的劳动力产品总收益的不同将导致工资率的差异，进而导致劳动力从农村转移到城市。因此，假定低技能劳动力潜在转移量ΔLSi是劳动力产品收益的间接效用函数，即ΔLSi=ψi|wi|ei。此外，低技能劳动力转移率λi的变化将导致工资率的变化，在劳动力产品总收益一定的情况下，当劳动力转移率λi较小时可导致一个较高的工资率，而当当劳动力转移率λi较大时可导致一个较低的工资率。

5.城市部门相关产品数量生产函数模型

物流生产制造业部门是一个高技能劳动力密集型部门，高技能劳动力被雇佣用于生产各种类型的Q型产品，这里假定所有的Q型产品具有相同的生产函数，则地区i的第j种Q型产品产出数量的生产函数模型为：

Qi，j=（gi，j/c）-（f/c） （12）

其中地区i的第j种Q型产品产出数量是该部门所雇佣的高技能劳动力数量，产品生产的固定投入和边际投入的一阶函数式。根据Sousa（2012）[11]和Markusen（2013）[12]的研究，地区i的S型产品产出可以采用以下形式的生产函数模型：

Si=L1-σ-βeiSi[∑Nij=1Q（φ-1）/φi，j]φ/（φ-1）σEβi（LSi0+λiPFiFi2）β（13）

其中地区i的S型产品产出是关于城市低技能劳动力数量LSi，E型产品数量，F型产品数量和各种类型的Q型产品产出的齐次生产函数。参数φ表示对不同种类的Q型产品的使用份额，当φ>1时，一定比例的Q型产品使得生产函数呈现出规模报酬递增的特性，而当φ<1时，一定比例的Q型产品使得生产函数呈现出规模报酬递减的特性。

二、仿真计算

（一） 实例相关数据

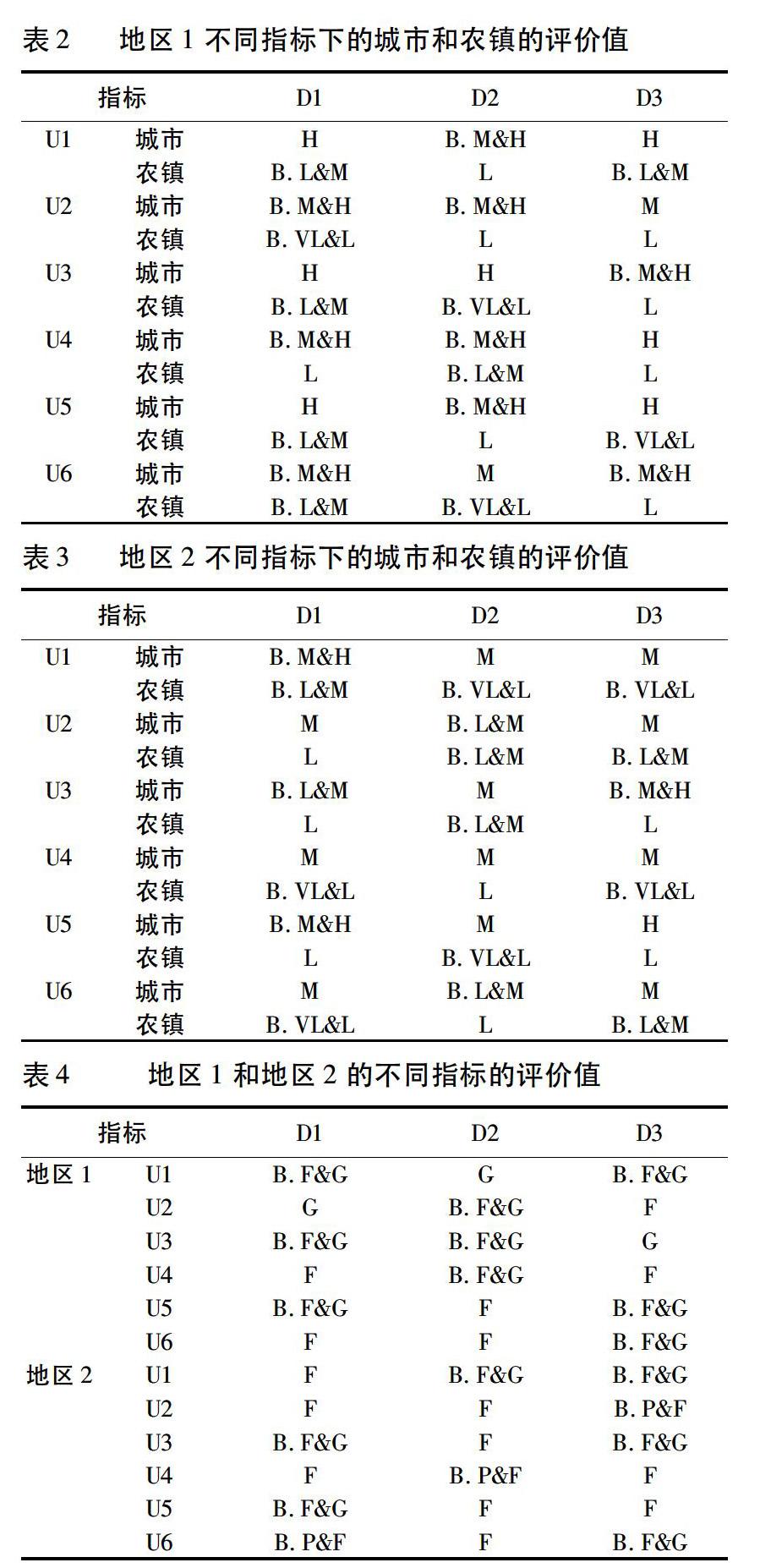
针对我国中西部地区典型的城乡“二元结构”形态，本文选取西部地区（如重庆、成都等）包含有对称经济结构的两地区（地区1和地区2），进行基于物流园区空间吸引的劳动力转移和产业集聚特征分析。地区1和地区2共同邀请3位专家D={D1，D2，D3}，运用表1中的模糊语言变量值对不同指标下城市和农镇的满意度及不同指标选择的满意度进行综合评价，见表2至表4。

为了验证和分析方法求解问题的有效性，本文参考相关研究文献[3，10，13-14]对部分参数进行赋值操作，设地区1和地区2的低技能劳动力数量为LF1=LF2=1500，地区1和地区2的城市初始低技能劳动力数量分别为LS10=400，LS20=500，高技能劳动力数量为g1，1=g1，2=g1，3=500，g2，1=g2，2=g2，3=400，地区1和地区2可耕种的土地面积为C1=100，C2=200，劳动力转移率的阻尼系数为τ1=04，τ2=03，地区1和地区2的F型产品生产函数的弹性系数为γ=015，地区1和地区2生产E型产品雇佣的劳动力数量分别为LE1=400，LE2=500，E型产品的生产相关系数为ζ=15，地区1和地区2的F型产品和Q型产品的价格分别为PF1=8，PF2=6，PQ1=5，PQ2=4，运输成本分别为d1=10，d2=8，地区1和地区2的劳动力潜在转移量与劳动力产品收益的相关系数为ψ1=ψ2=02，地区1和地区2的低技能劳动力与劳动力产品收益间接效用函数的幂指数为e1=e2=05，地区1和地区2的S型产品生产函数的弹性系数为σ=β=05，地区1和地区2用于Q型产品生产的固定投入和Q型产品生产的边际投入为f=4，c=2，地区1和地区2的Q型产品种类分别为N1=N2=3，地区1和地区2的不同种类的Q型产品的使用份额为φ=168。

（二）计算结果及分析

基于相关变量的定义，本文应用物流园区空间吸引的引力模型计算得到地区1的城市质量m11和农镇质量m12以及地区2的城市质量m21和农镇质量m22分别为m11=0648，m12=0498，m21=0574，m22=0467，进而应用公式（7）计算得到地区1和地区2的劳动力转移率分别为λ1=021，λ2=016。基于计算得到的劳动力转移率和相关变量的赋值定义，应用劳动力转移和产业集聚模型进行计算，得到如下变量数值：

地区1和地区2的E型产品数量为：E1=600，E2=750；

地区1和地区2的F型产品数量为：F1=999，F2=1109；

地区1和地区2的S型产品产出为：S1=307，S2=76；

地区1的N1种Q型产品产出数量为：Q1，1=Q1，2=Q1，3=246；

地区1的N1种Q型产品产出数量为：Q2，1=Q2，2=Q2，3=196；

地区1和地区2劳动力转移后城市低技能劳动力数量为：LS1=560，LS2=686。

通过上述计算数值可发现地区1的S型和Q型产品的产出高于地区2的相应产品的产出，而S型和Q型产品的产出规模是衡量地区物流发展水平和产业集聚程度的关键，进而也是地区整体经济发展程度的充分体现。此外，农镇和城市的差别导致农镇劳动力出现转移，且不同地区的经济发展差异导致劳动力的转移亦有差别，如地区1城市低技能劳动力的数量由初始的400人增加为当前的560人，而地区2的城市低技能劳动力数量则由初始的500人增加为当前的686人。

劳动力转移和产业集聚模型中已经充分考虑到受物流园区空间吸引的影响以及劳动力产品收益情况，农镇将出现向城市转移劳动力，城市将出现产业集聚的现象，且受到地区经济发展水平和条件限制等的影响，劳动力转移率与产业集聚密切相关，且劳动转移率的改变对产业集聚效应和地区差异也将产生一定的影响。

三、敏感度分析

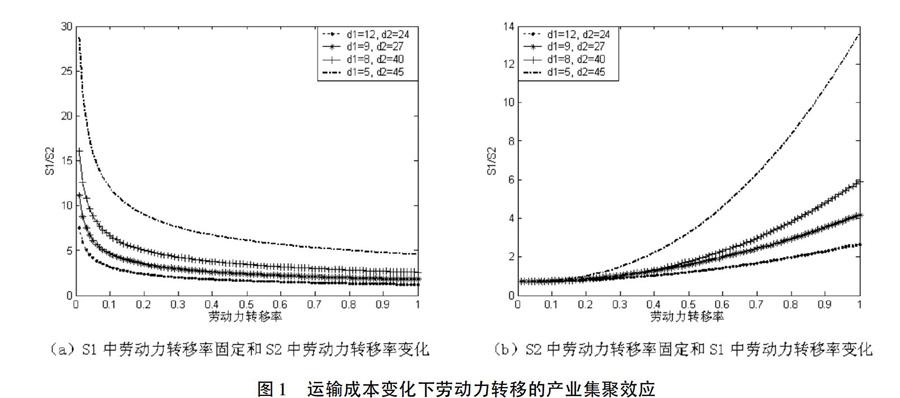
劳动力转移与产业集聚之间存在着一定的相关性，在不同运输成本条件下，劳动力转移率λ的改变将对产业集聚产生一定的影响。在设定了有关参数的初始值后分析劳动力转移率λ的改变与地区1和地区2的S型产品的比率S1/S2的关系，将有助于探讨不同地区间物流园区空间吸引的劳动力转移率变化对产业集聚的影响。如图1中（a）和（b）所示，x轴表示劳动力转移率λ，y轴表示地区1和地区2的S型产品的产出比S1/S2，劳动力转移率从0逐渐增大到1，运输成本分为四种情况设定：（1）d1=24，d2=12；（2）d1=27，d2=9；（3）d1=40，d2=8；（4）d1=45，d2=5。

在上述4种运输成本情况下，图1（a）中S1的劳动力转移率固定，随着S2中劳动力转移率的增加，地区1和地区2的S型产品的产出比S1/S2呈现缓慢下降的趋势，这说明了劳动力从农镇转移到城市将造成物流生产制造业向城市集聚；随着S2的劳动力转移率增加，集聚效应逐渐凸显，且地区1和地区2之间经济发展水平存在差异（地区1由于地区2），这也是导致S1/S2呈现缓慢下降的一个原因。在图1（b）中，S2中劳动力转移率固定，随着S1中劳动力转移率的逐渐增加，地区1和地区2的S型产品的产出比S1/S2呈现显著上升趋势，这同样说明地区1的劳动力从农镇转移到城市造成了物流制造业向城市集聚，而且从曲线的显著上升程度可以看出地区1的集聚效应总体上优于地区2的集聚效应。

此外，随着劳动力转移率的增加，在图1的（a）和（b）可以看出地区1和地区2的物流运输成本比率d1/d2越大，产业集聚效应也就越显著（参见图1（b）），特别是考虑到地区1和地区2之间存在经济差异，产业集聚效应越低，也就越容易导致劳动力的转移，进而造成产业集聚的萎缩，由此，地区间劳动力转移的现象也将出现。

劳动力转移与地区劳动力产品收益也存在一定的相关性，在设定不同的地区劳动力产品收益间接效用函数幂指数时，劳动力转移率λ的改变将对劳动力转移的集聚效应产生一定的影响。如见图2所示，x轴表示劳动力转移率λ，y轴表示地区1和地区2的城市低技能劳动力数量比率LS1/LS2，劳动力转移率从0逐渐增大到1，设定地区1和地区2的低技能劳动力与劳动力产品收益间接效用函数的幂指数分别为：（1）e1=e2=08；（2）e1=e2=06。

随着劳动力转移率的增加，由图2可见地区1和地区2的城市低技能劳动力比率将显著增长，不同地区的低技能劳动力与劳动力产品收益间接效用函数的幂指数也将影响城市低技能劳动力比率的增长幅度，图2中LS1/LS2曲线具有递增的正的斜率，且劳动力转移与城市低技能劳动力数量之间的关系呈正相关性，也即随着劳动力转移率的提高，地区间的劳动力数量变化呈现扩大的趋势。

综上所述，运输条件的优越性可为物流园区的空间吸引提供必要的辅助条件，由于物流发达的地区具有较好的地理区位优势，运输成本则相应较低，进而物流制造业的成本降低，可以说合理的运输成本是劳动力转移的一个动力和产业集聚的一个引力。此外，劳动力产品收益间接效用函数的幂指数是与产品收益密切相关的变量，高的幂指数将导致劳动力转移的增加，进而增加了劳动力供给，这相应的削弱了产业集聚带来的工资率上升的压力，从而成为产业集聚的另一个引力。

四、结论

本文针对两个均有农镇和城市且具有对称经济结构和相似生产函数类型的地区展开研究，分析物流园区空间吸引对劳动力转移率和产业集聚的影响。结果表明劳动力转移率与产业集聚密切相关，且劳动转移率的改变对产业集聚效应和地区差异会产生一定的影响；合理的运输成本是地区间与同一地区劳动力转移的动力和产业集聚的引力，高的劳动力产品收益间接效用函数的幂指数也是产业集聚形成的一个引力。因此，只有加快发展不同地区间及同一地区的城市与乡镇产品的物流制造业和服务业，才能提高低技能劳动力的产品收益，进而缩小城乡二元经济结构造成的地区差异，防止经济边缘化现象的出现。

参考文献：

[1]刘红梅，李国军，王克强. 中国农业虚拟水国际贸易影响因素研究——基于引力模型的分析[J].管理世界，2010（9）：76-87.

[2]杨胜刚，杨建模. 城市化与第三产业发展：基于湖南的实证分析[J].商业研究，2010（3）： 143-147.

[3]李扬. 西部地区产业集聚水平测度的实证研究[J].南开经济研究，2009（4）：144-151.

[4]海峰，阎欣，丁灿，邵校. 基于轴辐理论的现代区域物流网络节点选择[J].计算机集成制造系统，2012，18（6）：1299-1305.

[5]Nuzzolo，A.，Comi，A. City logistics planning： demand modeling requirements for direct effect forecasting[J].Procedia-Social and Behavioral Science，2014（125）：239-250.

[6]Chou，S. Y.，Chang，Y. H.，Shen，C. Y. A fuzzy simple additive weighting system under group decision making for facility location selection with objective-subjective attributes[J].European Journal of Operational Research，2008，189（1）：132-145.

[7] Wang，Y.，Ma，X.L.，Wang，Y.H.，Mao，H.J.，Zhang，Y. Location optimization of multiple distribution centers under fuzzy environment[J].Journal of Zhejiang University SCIENCE A，2012，13（10）：782-798.

[8]Wang，Y.，Ma，X.L.，Lao，Y.T.，Wang，Y.H. A Fuzzy-based Customer Clustering Approach with Hierarchical Structure for Logistics Network Optimization[J].Expert Systems with Applications，2014，41（2）：521-534.

[9]Kahraman，C.，Ruan，D.，Dogan，I. Fuzzy group decision-making for facility location selection[J].Information Sciences，2003（157）：135-153.

[10]敖荣军. 制造业集中、劳动力流动与中部地区的边缘化[J].南开经济研究，2005（1）：61-66.

[11]Sousa，J. D.，Mayer，T.， Zignago，S. Market access in global and regional trade[J].Regional Science and Urban Economics，2012，42（6）：1037-1052.

[12]Markusen，J. R. Putting per-capita income back into trade theory[J].Journal of International Economics，2013，90（2）：255-265.

[13]范剑勇，王立军，沈林洁. 产业集聚与农村劳动力的跨区域流动[J].管理世界，2004（4）：22-29.

[14]姚林如，李莉. 劳动力转移、产业集聚与地区差距[J].财经研究，2006，32（8）：135-143.

Abstract： In view of large-scale rural labor interregional migration and the expansion of industrial agglomeration level gap， this paper constructs the gravity model based on logistics park space attraction to determine the relationship between the “quality” in gravity model and labor migration rate， and considers the urban and rural “dual structure” of the Midwestern in China to construct the labor migration and industrial agglomeration models， and studies the labor migration and industrial agglomeration from the perspective of the logistics park space attraction. The relationship among the transportation cost， labor migration rate， labor production earnings indirect utility function power exponent， manufacturing production output ratio between different regions are studied through model simulation， which shows that the relationship between logistics park space attraction and labor migration rate is a positive correlation， and the relationship between transportation cost and industrial agglomeration effect is a negative correlation， and the industrial agglomeration effect and labor production earnings exist the characteristics of increasing returns to scale when labor migration rate increases.

Key words：logistics park； space attraction； labor migration； industrial agglomeration； dual structure

（责任编辑：厉新）