构造函数法在导数中的应用
2016-05-14柯淑芳
柯淑芳
“作差法”构造
证明不等式或解决不等式恒成立问题都可以利用作差法将不等式右边转化为0,然后构造新函数[F(x)],最后根据新函数[F(x)]的单调性转化为[F(x)min≥0]或者[F(x)max≤0来解决.]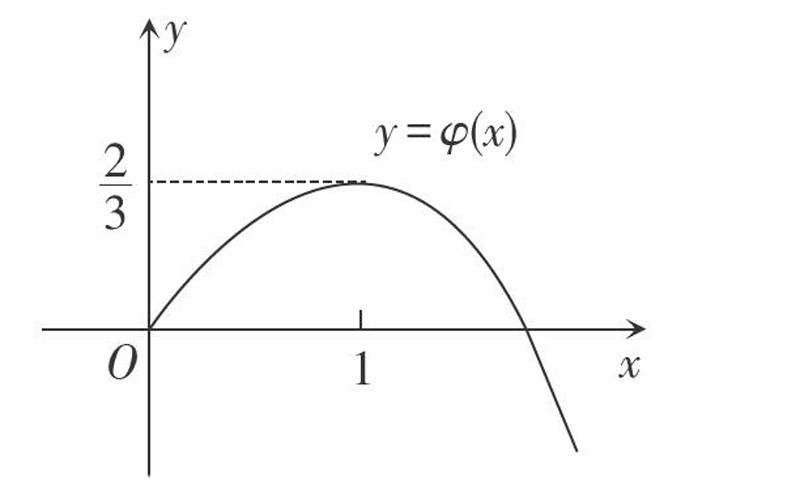
例1 设函数[f(x)=x1+x],[g(x)=lnx+12].
求证:当[0 证明 设[F(x)=f(x)-g(x)=x1+x-lnx-12],[0 ∵[F(x)=1+x-x1+x2-1x=-x2-x-11+x2?x<0.] ∴[F(x)]在(0,1]上单调递减. ∵[F(1)=12-0-12=0,] ∴[F(x)]≥0,当且仅当[x=1]时,等号成立. ∴当[0 “分离参数法”构造 恒成立问题中,求参数范围的问题,常常分离参数转化为[a≤F(x)min或者a≥F(x)max,]其中[F(x)]为构造的新函数. 例2 若不等式[2x?lnx≥-x2+ax-3]恒成立,则实数[a]的取值范围是( ) A.(-∞,0) B.(-∞,4] C.(0,+∞) D.[4,+∞) 解析 不等式[2x?lnx≥-x2+ax-3]恒成立, 即[a≤2lnx+x+3x]在(0,+[∞])上恒成立. 设[h(x)=2lnx+x+3x],则[h′(x)=(x+3)(x-1)x2(x>0)]. 当[x∈(0,1)]时,[h′(x)<0],函数[h(x)]单调递减; 当[x∈(1,+∞)]时,[h′(x)>0],函数[h(x)]单调递增. 所以[h(x)min=h(1)=4]. 所以[a≤h(x)min=4]. 答案 B 根据题干的“结构特征”猜想构造 1. 根据运算公式[f(x)?g(x)′=f(x)g(x)+f(x)g(x)]和[f(x)g(x)′][=f(x)g(x)-f(x)g(x)g(x)2来构造] 例3 已知函数[f(x)]的定义域是[R],[f(0)=2],对任意的[x∈R],[f(x)+f(x)>1]恒成立,则不等式[ex·f(x)][>ex+1]的解集为( ) A.(0,+∞) B.(-∞,0) C.(-1,+∞) D.(2,+∞) 解析 构造函数[g(x)=ex·f(x)-ex], 因为[g′(x)=ex·f(x)+ex·f(x)-ex=ex[f(x)+f(x)]-ex] [>ex-ex=0], 所以[g(x)=ex·f(x)-ex]为[R]上的增函数. 又[g(0)=e0·f(0)-e0=1], 所以原不等式转化为[g(x)>g(0)],所以[x>]0. 答案 A 例4 设函数[f(x)]满足[x2?f(x)+2x?f(x)=exx,][f(2)=][e28,]则当[x>0]时,[f(x)]( ) A. 有极大值,无极小值 B. 有极小值,无极大值 C. 既有极大值又有极小值 D. 既无极大值又无极小值 解析 构造函数[F(x)=x2?f(x)] 则[f(x)=F(x)x2′=ex-2F(x)x3,] [令h(x)=ex-2F(x),则h(x)=ex(x-2)x.] [∴h(x)]在(0,2)上单调递减;在[(2,+∞)]上单调递增. [∴h(x)≥h(2)=0]. [∴f(x)≥0,∴f(x)在(0,+∞)上单调递增.] 答案 D 2. 根据已知条件等价转化后再以“形式”来构造 运用下列形式的等价变形构造:分式形式[f(b)-f(a)b-a<1,] 绝对值形式[f(x1)-f(x2)][≥4x1-x2],指对数形式[1×2×3×4×…×n≥en-sn.] 例5 设函数[ f(x)=lnx+mx],[m∈R]. (1)当[m=e]([e]为自然对数的底数)时,求[f(x)]的极小值; (2)讨论函数[g(x)=f(x)-3x]零点的个数; (3)若对任意[b>a>0],[f(b)-f(a)b-a<1]恒成立,求[m]的取值范围. 解析 (1)当[m=e]时,[f(x)=lnx+ex],则[f(x)=x-ex2]. ∴当[x∈(0,e)],[f(x)<0],[f(x)]在[(0,e)]上单调递减; 当[x∈(e,+∞)],[f(x)>0],[f(x)]在[(e,+∞])上单调递增. ∴[x=e]时,[f(x)]取得极小值[f(e)=lne+ee]=2. ∴[f(x)]的极小值为2. (2)由题设知,[g(x)=f(x)-x3=1x-mx2-x3(x>0)]. 令[g(x)=0]得,[m=-13x3+x(x>0)]. 设[φ(x)][=-13x3+x(x>0)], 则[φ(x)=-x2+1=-(x-1)(x+1)], 当[x∈(0,1])时,[φ(x)]>0,[φ(x)]在(0,1)上单调递增;
当[x∈(1,+∞)]时,[φ(x)]<0,[φ(x)]在(1,+∞)上单调递减.
∴[x=1]是[φ(x)]的惟一极值点,且是极大值点.
因此[x=1]也是[φ(x)]的最大值点.
∴[φ(x)]的最大值为[φ(1)]=[23].
又[φ(0)]=0,结合[y=φ(x)]的图象(如图)可知,
①当[m>23]时,函数[g(x)]无零点;
②当[m=23]时,函数[g(x)]有且只有一个零点;
③当[0 ④当[m≤0]时,函数[g(x)]有且只有一个零点. 综上所述,当[m>23]时,函数[g(x)]无零点; 当[m=23]或[m≤0]时,函数[g(x)]有且只有一个零点; 当[0 (3)对任意的[b>a>0], [f(b)-f(a)b-a<1]恒成立[?f(b)-b 构造函数[h(x)=f(x)-x=lnx+mx-x(x>0)], ∴[h(x)]在(0,+∞)上单调递减. 由[h′(x)=1x-mx2-1≤0]在(0,+∞)上恒成立得, [m≥-x2+x=-(x-12)2+14(x>0)]恒成立. ∴[m≥14(对m=14,h(x)=0仅在x=12时成立).] ∴[m]的取值范围是[14,+∞]. 例6 已知[f(x)=(a+1)lnx+ax2+1], (1)讨论函数[f(x)]的单调性; (2)[设a<-1,?x1,x2∈(0,+∞),][f(x1)-f(x2)][≥4x1-x2]恒成立,求[a]的取值范围. 解析 (1)[∵x∈(0,+∞),∴f(x)=2ax2+a+1x.] [①当a≥0时, f(x)>0,f(x)在(0,+∞)上单调递增.②当-1 (2)不妨设[x1≤x2,]由(1)可知,当[a<-1]时,[f(x)]在[(0,+∞)上单调递减.] [则有f(x1)-f(x2)≥4x1-x2] [?f(x1)-f(x2)≥-4(x1-x2)] [?f(x1)+4x1≥f(x2)+4x2.] [构造函数g(x)=f(x)+4x,则g(x)=a+1x+2ax+4≤0]. [∴a≤(-4x-12x2+1)min.] [设φ(x)=-4x-12x2+1,x∈(0,+∞),] [则φ(x)=4(2x-1)(x+1)(2x2+1)2.] [故φ(x)在(0,12)上单调递减;][在(12,+∞)上单调递增]. [∴φ(x)min=φ(12)=-2.] [∴a≤-2.]
