矩形“搭台” 解几“唱戏”

2016-05-14王勇王海波

高中生学习·高二版 2016年6期

关键词：交点斜率题意

王勇王海波

矩形“搭台” 求解依托

例1 已知矩形[ABCD]中，[AB=22，BC=1].以[AB]的中点[O]为原点建立如图所示的平面直角坐标系[xOy].

（1）求以[A，B]为焦点，且过[C，D]两点的椭圆的标准方程；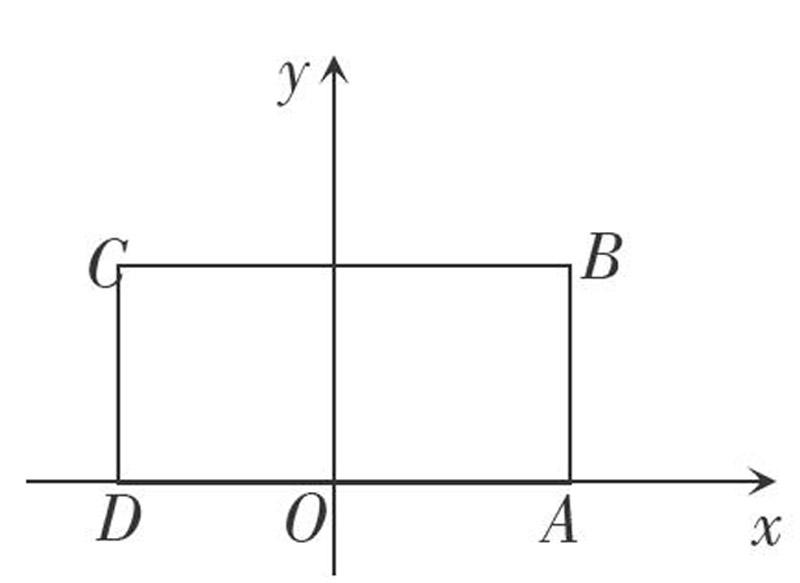

（2）过点[P（0，2）]的直线[l]与（1）中的椭圆交于两个不同的点[M，N]，是否存在直线[l]，使得以线段[MN]为直径的圆恰好过原点？若存在，求出直线[l]的方程；若不存在，请说明理由.

解析（1）由题意可得，点[A，B，C]的坐标分别为[（-2，0），（2，0），（2，1）].

设椭圆的标准方程为[x2a2+y2b2=1a>b>0].

则[2a=AC+BC]，即[2a=（22）2+12+1=4，a=2].

又[c=2]，所以[b2=a2-c2=2].

故椭圆的标准方程是[x24+y22=1].

（2）假设存在直线[l]，使得以线段[MN]为直径的圆恰好过原点. 由题意可知，直线[l]的斜率存在，可设直线[l]的方程为[y=kx+2].

由[y=kx+2，x2+2y2=4]得，[1+2k2x2+8kx+4=0].

因为[M，N]是椭圆上不同的两点，

所以[Δ=64k2-16（1+2k2）>0].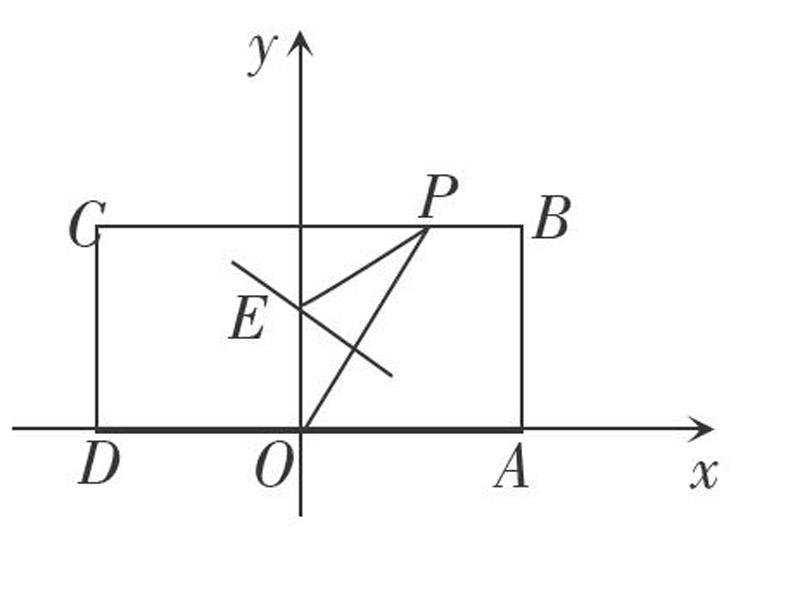

设[Mx1，y1，Nx2，y2]，

则[x1+x2=-8k1+2k2，x1x2=41+2k2].

若以[MN]为直径的圆恰好过原点，则[OM⊥ON].

所以[OM?ON=0]，

即[x1x2+y1y2=0?x1x2+（kx1+2）（kx2+2）=0]，

即[（1+k2）x1x2+2k（x1+x2）+4=0]，

所以[4（1+k2）1+2k2-16k21+2k2+4=0].

解得[k=±2]，显然满足[Δ=48>0].

综上所述，存在直线[l]，使得以线段[MN]为直径的圆恰好过原点，直线[l]的方程为[y=2x+2]或[y=-2x+2].

点拨本题以矩形为依托考查椭圆的标准方程，直线与椭圆、圆的位置关系，涉及到平面向量的有关知识，是一道难易适中的考题.

矩形“搭台” 巧求范围

例2 如图，在矩形[ABCD]中，已知[A（2，0），][C（-2，2）]，点[P]在[BC]边上移动，线段[OP]的垂直平分线交[y]轴于点[E]，点[M]满足[EM=EO+EP].

（1）求点[M]的轨迹方程；

（2）已知点[F（0，12）]，过点[F]的直线[l]交点[M]的轨迹于[Q，R]两点，且[QF=λFR]，求实数[λ]的取值范围.

解析（1）依题意设[P（t，2）（-2≤t≤2），M（x，y）].

当[t=0]时，点[M]与点[E]重合，则[M（0，1）].

当[t≠0]时，线段[OP]的垂直平分线方程为[y-1=][-t2（x-t2）].

令[x=0]得，[y=t2+44]，即[E（0，t2+44）].

由[EM=EO+EP]得，

[x，y-t2+44=0，-t2+44+t，2-t2+44].

[∴x=t，y=2-t2+44，]消去[t]得，[x2=-4（y-1）]，

显然，点[（0，1）]适合上式.

故点[M]的轨迹方程为[x2=-4（y-1）（-2≤x≤2）].

（2）当直线[l]的斜率不存在时，显然不合题意.

设直线[l]的斜率为[k]，[A（-2，0），B（2，0）]，要使直线[l]与点[M]的轨迹交于[Q，R]两点，画图易知，[kBF≤k≤kAF]，即[-14≤k≤14].

设[l：y=kx+12-14≤k≤14]，代入[x2=-4（y-1）]得，

[x2+4kx-2=0].

设[Qx1，y1，Rx2，y2]，则[Δ=16k2+8>0，x1+x2=-4k，x1x2=-2.]

由[QF=λFR]得，[x1=-λx2].

[∴（1-λ）x2=-4k，-λx22=-2.] 消去[x2]得，[（1-λ）2λ=8k2].

[∵][0≤k2≤116，∴0≤（1-λ）2λ≤12]，

即[2λ2-5λ+2≤0（λ>0）]，解得，[12≤λ≤2].

故所求实数[λ]的取值范围为[12，2].

点拨本题以矩形为载体考查动点的轨迹方程的探求和参数取值范围的求解，利用平面向量进行“包装”愈发加大了题目的难度.

矩形“搭台” 向量传接

例3 如图，在矩形[ABCD]中，[AB=8，BC=4]，[E，F，G，H]分别为四边的中点，且都落在坐标轴上. 设[OP=λOF，][CQ=λCF，][λ≠0.]

（1）求直线[EP]与[GQ]的交点[M]的轨迹[Γ]的方程；

（2）过圆[x2+y2=r2（0

解析（1）设[M（x，y）]，由已知得，

[P（4λ，0），Q（4，2-2λ），E（0，-2），G（0，2）]，

则直线[EP]的方程为[y=x2λ-2]，直线[GQ]的方程为[y=-λx2+2].

消去[λ]即得交点[M]的轨迹[Γ]的方程为

[x216+y24=1（x≠0）].

（2）如图，连接[OS，OT，ON]，由已知得，

[NS?NT=ON2].

又[ON⊥ST]，则[OS⊥OT].

①当直线[ST]的斜率不存在时，

则其方程为[x=±r（0

将其代入椭圆方程[x216+y24=1]得，[y=±4-r24].

又[NS?NT+r2=0] ，所以[r24-4+r2=0].

解得[r=455].

②当直线[ST]的斜率存在时，

设直线[ST：y=kx+m（m≠±2）]，

将其代入椭圆方程[x216+y24=1]得，

[1+4k2x2+8kmx+4m2-16=0].

设[Sx1，y1，Tx2，y2]，

则[x1+x2=-8km1+4k2，x1x2=4m2-161+4k2].

由[OS⊥OT]得，[x1x2+y1y2=0].

又[y1=kx1+m，y2=kx2+m]，

所以[km（x1+x2）+（1+k2）x1x2+m2=0].

则[5m2=16（1+k2）].

又点[O]到直线[ST]的距离为[r=m1+k2] ，

故[r=455].

而[455∈（0，2）]，满足题意，所以[r=455].

综上所述，所求[r]的值为[455].

点拨本题考查动点轨迹方程的探求方法（交轨法），直线与圆、椭圆的位置关系，平面向量的线性运算及数量积运算. 考查数形结合思想、分类讨论思想及运算求解能力.

矩形“搭台” 注重探究

例4 如图，矩形[ABCD]中，[AB=22，BC=2]，[E，F，G，H]分别是矩形四条边的中点，分别以[HF，EG]所在的直线为[x]轴、[y]轴建立平面直角坐标系，已知[OR=λOF，CR=λCF]，其中[0<λ<1].

（1）求证：直线[ER]与[GR]的交点[M]在椭圆[Γ：x22+y2=1]上；

（2）若点[N]是直线[l：y=x+2]上且不在坐标轴上的任意一点，[F1，F2]分别为椭圆[Γ]的左、右焦点，直线[NF1]和[NF2]与椭圆[Γ]的交点分别为[P，Q]和[S，T]. 是否存在点[N]，使得直线[OP，OQ，OS，OT]的斜率[kOP，kOQ，kOS，kOT]满足[kOP+kOQ+kOS+kOT=0]？若存在，求出点[N]的坐标；若不存在，请说明理由.

解析（1）参照例3（1）的解法可得，

直线[ER]与[GR]的交点[M]在椭圆[Γ：x22+y2=1]上.

（2）假设满足条件的点[N（x0，y0）]存在，若[NF1]，[NF2]有一条直线的斜率不存在，显然[kOP+kOQ+kOS][+kOT≠0]，所以[NF1]，[NF2]两条直线的斜率均存在，

故可设直线[NF1]的方程为[y=k1（x+1）]，其中[k1=y0x0+1].

直线[NF2]的方程为[y=k2（x-1）]，其中[k2=y0x0-1].

由[y=k1（x+1），x22+y2=1]消去[y]并化简得，

[2k21+1x2+4k21x+2k21-2=0].

设[P（x1，y1），Q（x2，y2）]，

则[x1+x2=-4k212k21+1，x1x2=2k21-22k21+1].

[∵OP，OQ]的斜率存在，[∴x1≠0，x2≠0，∴k21≠1].

[∴kOP+kOQ=y1x1+y2x2=k1（x1+1）x1+k1（x2+1）x2]

[=2k1+k1?x1+x2x1x2=k12-4k212k21-2=-2k1k21-1].