《电路分析》课程知识点脉络与数学知识的相关性

张永亮

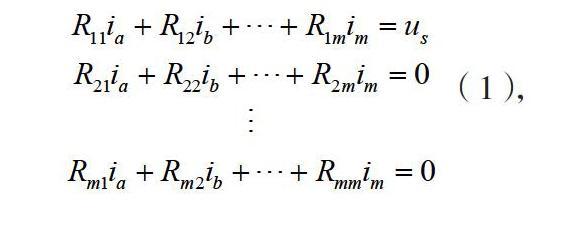
【摘 要】数学作为自然科学和工程科技的基础，其重要性不言而喻。本文通过实例给出了本科生专业基础课《电路分析》与数学知识之间的关联性。通过数学知识将《电路分析》的知识点融含贯通，起到举一反三的作用。

【关键词】《电路分析》 《线性代数》 《高等数学》 相关性

一、引言

《电路分析》[1]课程是通信工程、电子信息工程、电子科学与技术、测控技术与仪器、计算机科学类的专业核心课程，该课程是工科专业的重要专业基础课之一，也是电子通信、自动控制类研究生入学考试必考科目之一。该课程的掌握程度对后续课程的学习影响重大，例如《模拟电子技术》《信号与系统》《高频电子线路》等课程都是《电路分析》的后续课程，所以在知识点的安排上，该课程都属于重要的基础之一。该课程知识体系主要分为：电路的基本概念与定律、电阻电路的一般分析方法、常用的电路定理、动态电路时域分析、正弦稳态电路分析等。

该课程与数学结合紧密，知识点多，是高中物理电学部分与大学课程的过渡，所以一开始就必须把电路的基本概念夯实。电路的基本概念与定律包含：电路模型、电路变量、电阻元件与欧姆定律、理想电源、基尔霍夫定律、电路等效等。电阻电路的一般分析方法包括：图与电路方程的对应关系、和独立方程、法和法、回路法与网孔法、割集法与节点法。电路定理包括：齐次定理和叠加定理、替代定理、等效电源定理、最大功率传输定理。动态元件包括：电容元件、电感元件。动态电路的时域分析包括：动态电路的方程及其解、电路的初始值、一阶电路的零输入响应与时间常数、一阶电路的零状态响应、一阶电路的全响应（三要素公式）等。如此众多的知识点，如何由一条主线来牵引，既方便教学又有助于学生掌握知识点，是值得研究与总结的。

二、《电路分析》与数学问题的关联性

《电路分析》课程中用到的数学知识主要线性代数中矩阵方程的解、高等数学中微分方程的解法等知识点。

（一）《电路分析》与《线性代数》关联性

线性性质[2]是线性电路的基本性质，包括齐次性和叠加性。齐次定理和叠加定理是线性电路具有齐次和叠加特性的体现。齐次定理：对于具有唯一解的线性电路，当只有一个激励源作用时，其响应与激励成正比。下面从数学的角度来论证齐次定理的正确性。

假设某电路仅在网孔a中有一电压源us，其网孔方程如式（1），系数行列式如式（2），网孔a的电流的表达式如式（4）所示。其中是常数，与电路结构和电路元件参数有关，与激励无关。这是线性代数知识在《电路分析》中的典型应用示例。

（二）《电路分析》与《高等数学》关联性

为了说明二者之间的关联性，以二阶电路的响应为例进行说明。电路如图1所示。该图为RLC串联电路，以电容电压uc（t）作为电路的响应。由基尔霍夫电压定律（KVL）可得

可以看出式（7）是关于电容电压uc（t）的二阶微分方程，求解电容电压时可利用高等数学中微分方程的解法[3]，由本例可看出《电路分析》与《高等数学》的联系。

三、结论

本文通过举例说明《电路分析》课程与《线性代数》《高等数学》知识点之间的内容关联性，从数学的角度推导出电路的特性，而不是单纯的填鸭式教学，让学生做到知其然，更知其所以然，从而达到更好的教学效果，大大提高了教学质量。

【参考文献】

[1]张永瑞.电路基础（第二版）[M].北京： 高等教育出版社，2004.

[2]同济大学数学系.线性代数[M].北京： 高等教育出版社，2014.

[3]同济大学数学系.高等数学[M].北京： 高等教育出版社，2014.