如何上好《函数的奇偶性》这一课

张惠

函数的奇偶性是函数的重要性质，教材中是先从日常生活中的诸多对称现象来唤起研究函数对称性的意识.接着用两个熟悉的函数f（x）=x2与f（x）=-[SX（]1[]x[SX）] （x≠0）的图象为引例，直观地刻画出函数图象的两种特殊的对称性：前者关于y轴对称，后者关于原点对称. 以此为情境按特殊到一般的思维方式提出本课的研究课题：怎样用数量关系来刻画函数图象的这种对称性？

一、优化步骤，杜绝出错，让学生运用起来更顺手

教材中除了例6（3）与例7外，其他的例子都是学生初中所学的一次函数与二次函数，而且定义域一律都是

，学生用定义去判断函数的奇偶性，不会有太大的困难；但这也会造成一个认识上的误区，即不重视对函数定义域的研究与判断.虽然最后提出“具有奇偶性的函数，其定义域具有怎样的特点？”这个问题，但仍没有提到一个相当重要的位置来，这也正是我们要采取措施来进行补救的地方.判断一个函数的奇偶性，我们不要仅仅让学生直观观察图象来作出某些判断，更重要的是要让学生养成用定义来研究这个问题的习惯，因为多数的图象对于中学生而言不容易画出来.我们要教给学生一个明确的判断步骤，杜绝学生出现忽视定义域的错误.

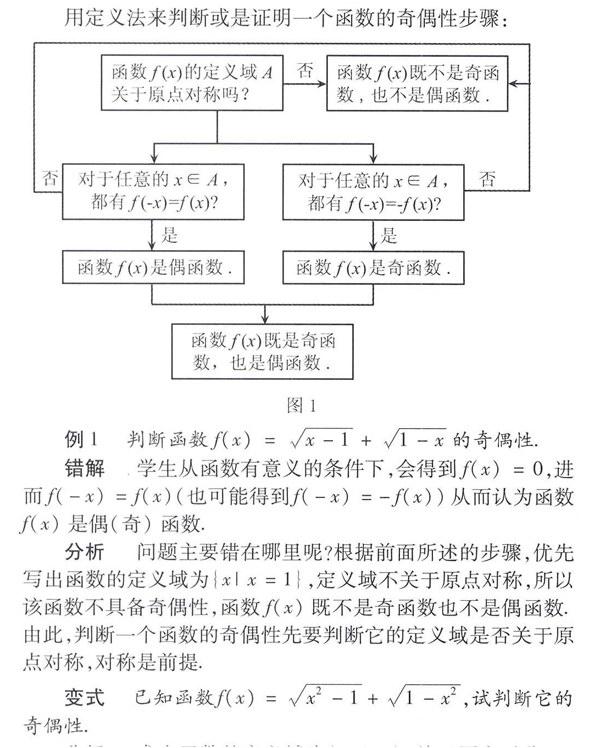
用定义法来判断或是证明一个函数的奇偶性步骤：

分析求出函数的定义域为{-1，1}，关于原点对称.又此时f（x）=0，易证函数f（x）既是奇函数又是偶函数.也许有些同学在求得函数的定义域后，不知道化简函数的表达式，而去判断它的奇偶性，这样做的结果往往是得出错误的结论.

二、巧设问题，促进思考，培养学生的思辨能力

学生对于概念的理解与掌握不是一蹴而就的，而是一个螺旋上升的过程.在后继学习了指数函数与对数函数之后，我们还要做到：提供反面教材，培养学生的思辨能力，在函数中，我们经常会碰到需要综合应用函数的奇偶性与单调性来解决的问题，但学生往往对于函数的这些性质，采取思维定势，“挂靠”某一特殊的函数，从而得到错误的结论.

可见，教材上函数奇偶性的概念不难，而函数奇偶性概念的细致性、严谨性和科学性，以及奇偶性质的发掘与应用不在正文，而是散落在例习题中.因此，要上好这一课，首先要立足教材，吃透教材的编写意图，挖掘例习题的功能，提炼例习题隐含的意义，才能让学生少做题，并且在做题中明白定义域优先，先化简再判断，数与形紧密结合，特殊与一般随时结合这些道理.