高中数学中函数概念教学的思考

吴长山

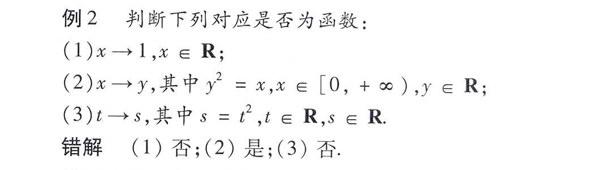
经过几轮高中数学的教学工作，发现很多同学都在说数学难，数学题不容易得分，高三复习的时候都在抓“八个C级”.其实，好多同学给我的感觉是基础不牢固，对基本概念的理解还有欠缺.不注重“基石”，所以“上层建筑”怎么都不稳固.高中数学最核心的内容：函数，函数的思想和方法贯穿整个高中数学.函数与不等式、方程、数列等许多内容息息相关，掌握了函数的相关内容，高中数学就向你敞开了大门.

从而我们来看一下函数的概念，高中函数的概念和初中我们所学的函数的概念有所不同，是对函数的概念更严谨的定义.理解了函数的概念，我们就可以说掌握了开门的钥匙.

一般地，设A，B是两个非空的数集，如果按某种对应法则f，对于集合A中的每一个元素x，在集合B中都有唯一的元素y和它对应，那么这样的对应叫做从A到B的一个函数，通常记为

错解（1）是；（2）否.

错因分析（1）没有理解“A中每一个”，集合A中有一个元素5按对应法则应该对应10，但是10不在B集合中，所以不是函数；（2）认为B集合中有一个元素0在集合A中没有元素和它对应，我们只要求“A中每一个元素，在B中都有唯一元素和它对应”，至于集合B中是否多出其它数字，不影响它满足函数的定义.

为了进一步理解函数的概念，我们再看下面的例题.

错因分析（1）认为1不是变量，所以不是函数.而从函数的定义来看，其满足函数的定义，所以它是函数；（2）只看到了“A中每一个”没有注意“B中唯一”.比如集合A中存在一个元素1，按对应法则在集合B中有±1两个元素和它对应，所以不满足函数定义；（3）误认为不是x、y，所以不是函数.函数就是从一个非空数集到另一个非空数集的单值对应.不论其是用什么字母表示，关键是看是否满足函数定义，只要满足它就是函数，不满足就不是.

通过上述的例题可以加深我们对函数概念的理解，重点记忆“两个非空数集”、“一个对应法则从A到B”、“A中每一个”、“B中唯一”这几个关键词.

还要指出的是给定函数时，要注明定义域是什么，对已知函数表达式的函数，如果没有注明定义域，那么认为函数的定义域是使函数表达式有意义的输入值的取值范围.