应用反比例函数知识解决生活问题

刘建凤

生活离不开数学，数学也离不开生活，数学知识源于生活但又高于生活.我们学习数学就能在实际生活中应用数学知识解决生活问题.本章我们学习了反比例函数知识，下面我们就来看看如何应用反比例函数知识解决生活问题.

苏科版八年级下册教材140页提到，阿基米德发现了著名的“杠杆原理”，如图1，杠杆平衡时候有：动力×动力臂=阻力×阻力臂.所以他豪言：给我一个支点，我能撬动地球.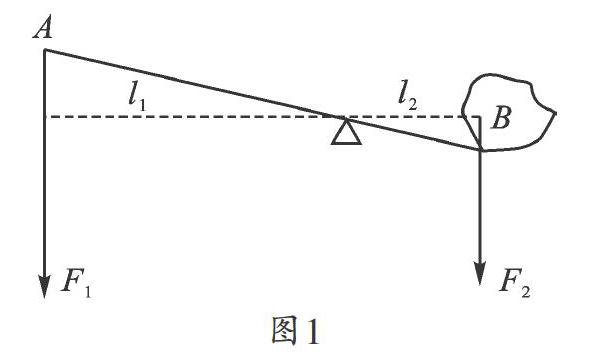

我们知道这是不可能真的实现的，只存在于理论中，但是实际生活中我们却实实在在地应用着“杠杆原理”.例如开门、骑车、曲臂运用等都是利用杠杆原理.很多常用工具就是运用杠杆原理将我们施加的力变大，从而帮助我们解决很多生活难题.但是实际生活中也有不良商贩利用秤的杠杆原理来欺骗消费者.

首先我们借助图2来分析一下秤的原理.

如图2所示的杆秤以绳纽悬点为支点O，秤钩悬点为A，秤锤悬点为B，称量时，提纽两侧受两个拉力F1、F2（即物体的重力和秤锤的重力）作用，两力的力臂分别为OA、OB，由杠杆原理得：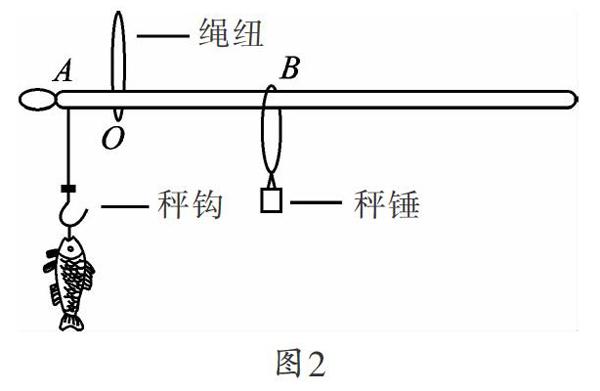

F1·OA=F2·OB.

设秤锤和物体的重分别是m锤和m物，则有

m锤·OA=m物·OB.

所以，m物=m锤·OA/OB.

下面我们就来看看不良商贩欺骗消费者常用的两种方式.

（1） 手抬秤杆

在称量时，商贩为了迎合人们喜欢称旺秤的心理，手在滑动秤锤细绳的过程中，有意滑向刻度值大于货物的实际质量的位置，并顺手用力向上扬起秤杆，迅速抽手，秤尾由于惯性上翘，商贩会在秤尾还未下倾时，立即报出物重并放下货物.本质上是OB比实际大，那么m物就比实际小.

（2） 手压秤头

商贩在称量时，将提秤的手指头散开，用其中一手指向下施力压住秤头，增加了物体的视重. 本质上是m锤比实际大，那么秤得的m物就比实际要大.

（作者单位：江苏省常州市武进区前黄实验学校）