走向发现，从算法多样化到算法优化

吴素梅

一、缘起

在同课异构“两位数乘两位数笔算”中发现，一些教师对计算教学已形成一般流程：“导入→探究→交流→优化→拓展”。笔者明显感觉到几个共性问题：一是算法多样比较粗糙，流于形式；二是教师预设的方法不出现便不罢休，“逼”出算法；三是思维挑战性不强，盲目优化。

对学生而言，本节课教学目标定位在哪里？在鼓励算法多样化的同时如何正确处理“多样化”与“优化”之间的关系？笔者带着这些问题，对“两位数乘两位数笔算”的教学进行了如下的思考与实践。

二、思考

提倡算法多样化的目标之一是培养运算能力，它要求学生在计算过程中理解运算的算理，寻求合理简洁的运算途径解决问题。可以概括为：理解算理、发现算法，重在运算的道理及算法的发现。我们强调优化，就是要从探讨算法多样化的过程中，创设认知冲突，让学生经历一个独立思考、自主学习、合作交流与思维碰撞的创新过程，从而走向发现，让其中蕴含的思考价值熠熠生辉。理念更新，教师有必要从两个层面上做到教学策略的改变。

第一层面，善于发现学生。教师需改变传统说教观，主动观察学生，关注到每位学生，挖掘学生的潜能，放手让学生在课堂上分享、交流，算法多样“呼之欲出”。

心理学研究发现：影响学生学习质量的因素除了教师及课程的因素外，学习者自身的因素亦不容忽视，以生为本，是课堂教学的出发点。

学生的思维是有不同层次的，能力强的学生思维层次高，能直接抓住问题的本质，能力弱的学生正好相反。教师在课堂教学中要根据不同学生的学情和个性差异实施分层教学，鼓励不同的学生从不同的角度认识问题，尝试用不同的方式表达自己的想法，提升用不同的知识与方法解决实际问题的能力。教师在组织教学活动时，既要尊重学生的个性差异，关注学生独立思考的过程与方法，又要让学生积极参与互动，让学生学会合作与交流，学会分享和展示自我。

第二层面，善于引导学生发现。以自己对学生生成的发现，促进学生的自我发现，从而引发彼此的发现，算法优化“水到渠成”。

“算法多样化”不是单纯的方法多样，不是以多代优或一味求多，而是学生在教师的引导下通过多种方法的感受、体验、对比，发现规律，生成算法，在互动交流中明晰算理，有意识地使方法更加优化或较优化的过程。

教师不能代替学生思考，不能直接主导学生按自己的想法进行操作，只有放手让学生做了、说了，才知道会出现怎样的情况，我们只能做好充分的准备，面对课堂上的各种生成。鼓励课堂生成，培养学生良好的思维习惯，促成其发现问题、解决问题能力的发展不是一蹴而就的，需要一个长期的过程。即便学生提出的方法有的只停留在表层，抑或繁琐或不够全面，这时需要发挥教师“点石成金”般的引导作用，促其亲身经历由点到面、由浅入深、由繁到简的习得过程，在探究中发现规律，悟出方法。

三、实践

（一）情境导入，感受需要

授课时，利用主题图，让学生寻找有效数学信息（每套书有14本，王老师买了12套。一共买了多少本）并初步交流各种想法，如估算、笔算等。接着教师重点引导学生小组合作（14×12，你会计算吗？把你的方法试着用点子图表示出来）。教学新方法，应从实际的需要出发，使数目的计算有相当的依据，无意义的问题不选用。操作方法：利用点子图（横14个，竖12个），请学生数一数、想一想、圈一圈，尝试计算。目的是唤起学生对两位数乘一位数，两位数乘整十数口算的原有认知经验。

（二）积极寻找，生成算法

算法是需要在学生寻找、发现的过程中产生的。

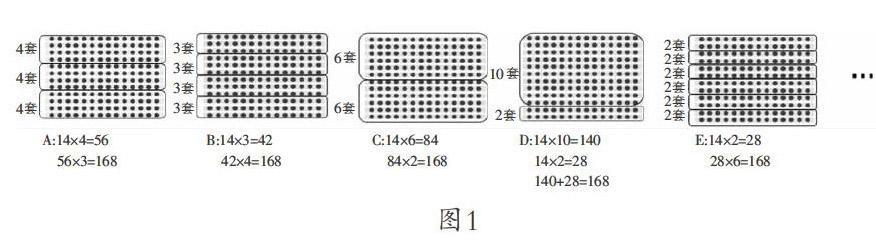
学生自主尝试后，组织反馈。结合点子图学生会出现多种算法，教师有意识地进行了分类（图1），引导学生发现：A、B、C、D、E五种方法都是把其中一个因数拆分之后，转化成了以前学过的算式。学生的发言是积极的，他们很快就会发现这些方法都是基于“先分后合”。学生感受到分开以后，数变小了，就会算了，实际上就是把两位数乘两位数转化成两位数乘一位数的乘法。那么，哪种方法与其他方法有明显不同呢？学生们通过观察、比较，很容易就会发现方法D不同，是先求10套几本，再求2套几本，最后求出12套的本数，教师对方法D做重点评析，目的是为后续竖式计算的教学及明晰算理做好铺垫，在比较过程中培养学生的分析能力和优化意识。到此，一部分学生自然想到了用竖式的方法来计算，应怎样用竖式进行计算，学生的探究热情已然高涨。

（三）激发思维，内化算理

算法即运算途径，即基于算理，能使运算合理简洁进行的方法。也就是说，无论心算、口算、笔算，或面对整数、小数、分数等，任何算法及其变化、演进、技巧，均基于算理。运算能力是由算理到算法，从算的“慢、笨”到“快、巧”的探索过程中逐步形成的。只有算理的内化才能促成算法的真正形成，教师要做的是激发学生思维，积极投入方法的探究过程。

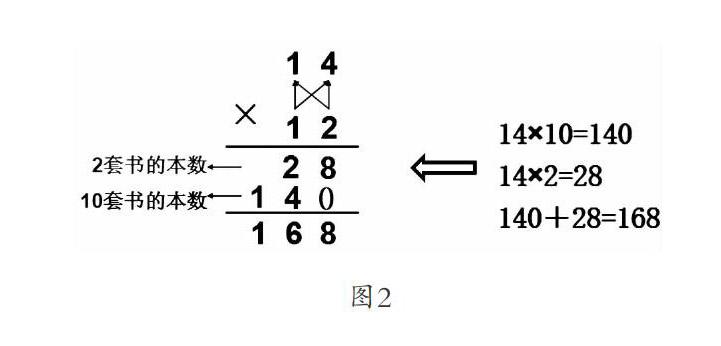
学生生成的多种算法，它们与竖式有联系吗？有什么样的联系呢？教师要尊重学生，让学生多想、多动、多说，思维进一步深入。学生思考：14×4×3、14×3×4、14×2×6、14×6×2、14×10+14×2和14×5+14×5+14×2等。其中哪种方法能恰当地体现竖式的计算过程？教师再次引导学生结合点子图，说一说竖式计算的每一步依据，在学生已经初步掌握竖式计算方法的基础上，利用直观的点子图，使学生留下清晰的思维轨迹，使学生反馈的学习成果得以证明。（图2）学生计算的方法不完全相同，但乘法竖式计算的基本思路形成了。从而让学生进一步理解了计算的道理，促成算理的内化。

（四）引导发现，优化算法

算法确立的标准是建立在比较基础上的合理与简约，在比较中“探索→总结→运用→拓展”。

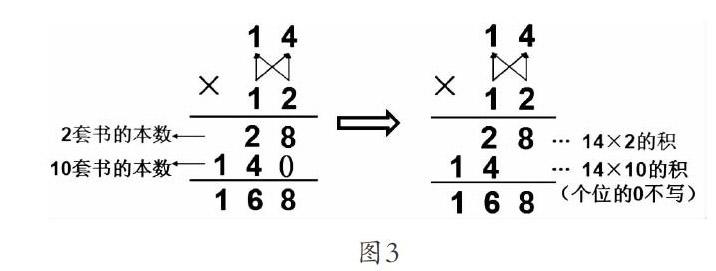
首先是基于算理解决问题，引导学生对横式与竖式建立联系，然后把得到的竖式进行比较，最后得到基于位值的一般竖式算法。（图3）有时学生的错误给课堂提供了很好的学习资源，教师要研究错误的产生，通过一起分析，一起比较，引起高度重视，避免计算时再次出错。例如，教师指出：“刚才有位同学算14×12得到的积是42，你知道他错在哪里了吗？”通过让学生纠错的办法来确定算法，也未尝不是好办法。

四、反思

引导学生寻找和发现，并不是一种比讲授更复杂的教学方式。只要给学生留出较充分的探索空间，教师再多一些恰当引导，每个算法都可能被学生找到。从学生的全面发展、健康成长出发思考计算能力的培养问题，我们要努力做到以下“三适”。

（一）适度失控

算法是技能，是经过寻找、发现得到的技能。我们大部分时候都不放心学生，于是，学生在课堂上的每个时间点、每个节点上要干什么，我们都规定得特别详细，这样的教学设计让学生失去了自主发展的空间。只有让学生的思维开放，产生碰撞，从求异思维中进一步找寻计算的一般方法，形成基本的运算技能，才能走向深度教育。教师要给学生更多的时间、空间，搭建适度失控的开放性平台，让学生在课堂上尽可能地施展才能。

（二）适当点拨

提倡算法多样化，课堂上的适当点拨最为重要。课堂上学生的生成形式多样，要求教师善于捕捉其中有价值的内容，揣摩学生思路，洞悉真实想法，进而适当地加以点拨，引导他们讲清自己的算法。算法多样化是宝贵的课堂生成性资源，既是师生互动，也是生生互动的产物，它离不开教师在其间发挥的重要作用。

（三）适时优化

计算教学，教师要重视引导学生探索计算的过程。当学生呈现多种算法后，教师不要急于评价某种方法的优劣，而是适时引导自主体验，让他们沉浸于数学课堂，在寻觅、还原最简单直观的道理和方法的过程中，使算理和算法融为一体，提高思维的深刻性。教师要瞻前顾后，找准时机，让学生在不同的情况下学会灵活选择恰当的方法。

（作者单位：福建省闽清县白中镇中心小学）