关于算法多样化的思考与实践

孙家芳

【编者按】“计算能力”是学生学习数学的必备能力。计算能力的培养，是小学数学教学的根本任务之一。教师对学生计算能力培养的日趋重视，“算法多样化”一词，也常被教师们挂在嘴边。课堂上百花齐放、百家争鸣的态势成为不少教师在处理计算教学时所追求的理想状态，却对算法多样化的存在意义、算法优化处理的认识有所偏差。本期专辑聚焦“小学数学算法多样化教学”。

当前，算法多样化已成为教师习以为常的教学行为，算法多样化与算法最优化的理念也日益深入教师的内心。然而，算法多样化的现状如何？为什么会有算法多样化？算法多样化的目的是什么？算法多样化的时机怎样把握？算法多样化有没有可遵循的模式？算法多样化的主人是谁？众多问题隐含在教学中，带着这些思考，笔者结合自己的教学实践和大家交流。

一、“算法多样化”在实际教学中的现状

在平日的教学中，我们经常看到教师们如此带领学生进行算法多样化的学习。

【原始案例】两位数加两位数进位加法的口算

布置研讨话题：请你用不同的方法计算37+45，并把你的思考过程写清楚，让别人看明白。

交流研讨：

师：谁来说说你是怎么算的。

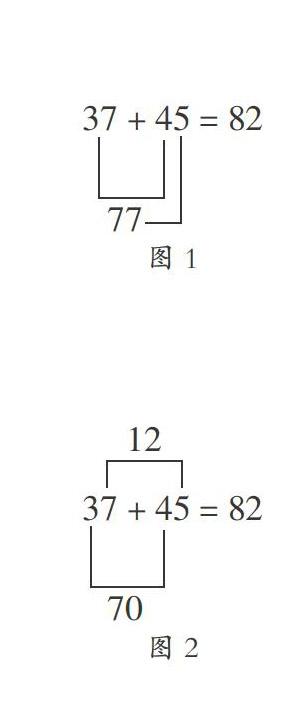
生：我先算37加40等于77，再算77加5等于82。

教师一边重复学生的语言一边画出思路图。（图1）

师：他的想法对不对？

师：还有不同的方法吗？

生：我先算30加40等于70，再算7加5等于12，最后算70加12等于82。

教师一边重复学生的语言一边画出思路图。（图2）

师：他的想法对不对？

师：还有不同的方法吗？

生：我把45分成3和42，先算37加3等于40，再算40加42等于82。

教师一边重复学生的语言一边画出思路图。（图3）

师：他的想法对不对？

师：还有不同的方法吗？

生：我把45分成43和2，先算37加43等于80，再算80加2等于82。

教师一边重复学生的语言一边画出思路图。（图4）

……

在此基础上，教师又组织学生按照类似的思路，将37进行分解研究，衍生出类似的算法，然后教师组织学生小结并择优。

师：就是一道简简单单的计算题37+45的和，我们就能用8种方法进行计算，多棒啊。这8种方法中你喜欢哪个？

生：我喜欢第一种方法，因为它是用第一个加数和后面的整十数相加。

师：哦，是这样，还有喜欢别的方法的吗？

生：我喜欢第二种方法，因为它是十位数和十位数相加，个位数和个位数相加，最后再求和。

……

师：就像大家说的，你喜欢哪种方法就用哪种方法吧。

从表面上看，学生和教师共同经历了算法多样化的过程：首先，学生在教师布置的话题下进行独立思考，然后把自己的思考记录在纸上；其次，学生在教师的组织下进行交流。在交流的过程中，每个学生都展示了自己的想法，然后补充其他的想法；最后梳理出8种方法，并从中选择自己喜欢的方法。

该教学过程看似没什么问题，但仔细思考后笔者产生了这样的疑问：①在每个学生表达自己想法的时候别的学生是不是在认真的倾听？②学生听一遍别人的想法是不是就能内化为自己的想法？③在学生交流算法的过程中教师的作用是什么？④算法多样化的目的是什么？算法多样化给学生的是知识教育还是全人的养成？算法多样化可以为学生的终身成长奠定什么？

二、怎样进行算法多样化

同样的交流过程，笔者只是建议教师们增加这样的引导语。

【改进后的案例】

师：谁来说说你是怎么算的。

生：我先算37加40等于77，再算77加5等于82。

师：（对学生的发言作价值判断后）谁听见他说的了，再给我们说一说。

师：（学生重复一遍后）谁又听见他说的了，再给我们说说。

师：（学生再重复后）两个人互相说说他的思路。

师：（学生相互重复后）谁能把他的想法用算式表示出来让我们看明白。（图1）

师：这位同学的思路是什么，谁能结合这个算式说说。

师：（学生重复一遍后）谁再结合这个算式给我们说说。

师：（学生重复后）两个人结合这个算式互相说说他的思路。

师：（慢慢地带领学生梳理）这位同学的想法是先算37与40的和，再把这个和加上5即可。

师：除了这个想法，还有不同的方法吗？谁来补充。

生：我先算30加40等于70，再算7加5等于12，最后算70加12等于82。

重复上面的过程。

师：（梳理）现在我们有两种方法了，第一种方法是先算37与40的和，再把这个和加上5；第二种方法是先算两个整十数的和，再算两个个位数的和，最后把它们加起来。

师：除了这两个方法，还有其他方法吗？

对比两个案例的第一个环节，相同的是学生经历同样的过程，不同的是增加了两次确认和一次梳理。

第一次确认的目的是让每个学生先听清楚他人是怎么想的，为学生有能力辨析他人的想法和自己的想法是否一样奠定基础，也为后面的算式表征奠定基础。第二次确认是在学生用算式表征后，这次确认的目的是让每位学生都清楚地知道语言表征和符号表征的意思是相同的，提升学生两种语言的互译能力。梳理的过程是学生再现的过程，不仅可以给学生丰富的表现支撑，也可以培养学生有序思维，为后面不同思路的研究奠定坚实的基础。

三、教育的目的是什么

虽然我们今天交流的是算法多样化的教学，然而，笔者更想借助算法多样化的交流，和同行们共同思考教学的目的是什么，教育的目的是什么，教育改革的目的又是什么？我们的教育改革应该让学生有实际获得感，让家长有实际获得感。这不仅应成为所有教育改革的出发点，也应该是归宿点，并在改革实践中成为判断改革与否的唯一标准。（北京市教委委员，李奕）

我们的教学让学生有哪些实际获得感呢？笔者想从三个维度和大家交流。

1. 让学生获得知识。

毋庸置疑，无论什么内容的课都要让学生获得知识，获得的意思是取得、得到，获得知识就是取得、得到知识，那在“两位数加两位数进位加法的口算”这节课中学生获得哪些知识？我们细细分析。

（1）确定学生获得知识的基本思路。学生在学习任何一节课之前都是有学习起点的，经过师生40分钟的劳动就会有学习终点，我们通过学生学习起点与学习终点的知识差确定获得了哪些知识。

（2）分析“两位数加两位数进位加法的口算”这节课学生获得的知识。第一环节：教师通过布置研讨话题“请你用不同的方法计算37+45，并把你的思考过程写清楚让别人看明白”了解学生的学习起点。第二环节：通过学生之间的相互交流，使学生知道除了自己采用的方法，还有其他的思路，并学会这些思路，知道哪些方法比较好，哪些方法麻烦些，这应该是本节课的学习终点。那么，这节课学生获得的知识应该是由原来的两三种方法增加到最后的八种方法。但是因为教师在研讨过程中确认、梳理的比较少，基本形成课前会的课后还会，课前不会的课后还不太懂，因此学生获得的知识比较少。

（3）学生获得知识的基本方法——有效的确认、梳理。

有效的确认首先来源于对学生的发言作价值判断而不是对错判断。也就是说，我们在认真倾听学生发言的过程中，要努力思考学生发言的意思是什么，和本节课的教学目标是否相关，怎样借用学生的发言引导全班学生进行更深入的研讨。当我们确认学生的发言有价值的时候，我们要进行确认，通过不断地确认，把一个学生的想法变成全班的想法，在此基础上引导学生进行更深入的思考。学生经历这样的过程，不断地将别人的想法听清楚、想明白，在此基础上进行梳理，不断地把别人的想法内化为自己的想法，也使得学生的思维更加有序化。

2. 让学生获得见识与视野。

任何一节课没有知识是不行的，但仅仅获得知识也是不行的，我们还要让学生获得见识与视野。见识，见多才能识广，这是一个人对事物的看法和态度；视野，是视力所及的范围。让学生获得见识与视野，就是让学生见得多、看得远。

怎样让学生获得见识与视野？教学中可以通过不断地确认与梳理，使学生不仅知道自己的想法，还知道他人的，知道把他人的想法不仅要听清楚、想明白，还要内化为自己的想法，知道天外有天、人外有人。

如果我们每一天的数学课都让学生在倾听、交流、研讨中度过，那么，学生会慢慢形成一种习惯，一种做事情首先要有自己的想法，然后要听清楚他人的想法，并不断地把他人的想法变成自己想法的习惯，长大后，学生不仅有独立思维和清晰、连续表达的能力，善于倾听的能力，归纳总结和提取有效信息的能力等，还会尊重人、尊重思维，谦和、包容、海纳百川，我们就为孩子的一辈子奠定了良好的基础。

3. 让学生获得核心素养。

《21世纪学生发展核心素养研究》一书中指出，核心素养是适应学生终身发展和社会发展需要的必备的品格和关键能力。就数学学科而言，必备的品格指的是数感、符号意识，具体体现在联系、语言、目标的转换、相对的严谨、反思；关键能力指的是运算能力、几何直观、数据分析观念、推理能力等。

具体到这节课，学生用生活形象语言、动作语言、数学图形语言、数字符号语言、连续性文本语言等不同的表征方式表达出对数的直觉，因此就有了不同的算法，算法多样化为学生提供一个交流的平台，在这个平台上，学生间读懂、沟通、分享、优化，展示了数学除了计算之外的另外两个非常重要的属性，一个是语言属性，即用数学的语言进行表达；第二个是工具属性，即把数学当作重要的工具来解决生活中的各种问题，通过数学，把所有问题量化出来，使每个人按照这样的标准做出同样的东西。

数学是让人认真的学科。学习数学，需要从生活现象中觉察有趣的结构，尽可能通过模拟操作来理解这些结构微妙之处，并尝试描述它，通过与他人的分享交流来简化、优化我们的描述，以使得他人真正理解到我们想要说明的，这一系列的活动可以帮助学生获得良好的核心素养。

（作者单位：北京市朝阳区教育研究中心）