三次参数曲线的区间扩展

李军成，刘成志（湖南人文科技学院数学系，湖南娄底417000）



三次参数曲线的区间扩展

李军成，刘成志
（湖南人文科技学院数学系，湖南娄底417000）

摘 要：为了在传统三次参数曲线中引入形状参数，通过将三次Ferguson曲线、三次Bézier曲线、三次均匀B样条曲线等传统三次参数曲线的定义区间由固定区间［0，1］扩展为动态区间［0，α］，构造了3种带参数α的三次参数曲线，分别称之为三次α－Ferguson曲线、三次α－Bézier曲线以及三次均匀α－B样条曲线．所构造的α－曲线是原三次参数曲线的同次扩展，不仅方程结构简单，继承了原曲线的性质，而且可通过修改参数α的值实现对曲线形状的调整，是一种简单有效的形状可调参数曲线构造方法．

关 键 词：三次参数曲线；区间扩展；形状可调

随着几何造型工业的发展，常常需要通过改变曲线的形状来满足各种几何造型的需要．Ferguson曲线、Bézier曲线、B样条曲线等作为传统几何造型方法虽然在表示曲线曲面时显示了较强的能力，但一旦边界条件或控制顶点固定，用这些方法表示的曲线曲面在形状修改或调整时就受到了较大的限制，从而制约了其在几何造型工业中的应用．NURBS曲线虽然能通过权因子对其形状进行适当调整，但由于采用有理形式，计算比较复杂，使得NURBS曲线在形状设计与分析中亦存在一定的局限性．近年来，为了克服传统参数曲线在造型上的不足，国内外许多学者开始构造较为实用的参数曲线模型，其中带形状可调的参数曲线逐渐成为研究的热点．为了构造带形状可调的参数曲线，国内外学者提出了许多不同的方法，其中最为常见的有带形状参数的多项式曲线［1－5］、带形状参数的非多项式曲线［6－10］、带形状参数的奇异混合曲线［11－14］．这些方法虽然可通过修改形状参数值有效调节曲线形状，但其代价是所构造的曲线模型的次数提高了，或者曲线的方程结构变得复杂．

无论采用何种方法构造形状可调的参数曲线，其主要目的都是为了在传统参数曲线中引入形状参数，通过修改形状参数的取值实现对曲线形状的修改或调整，以此来改善传统参数曲线造型方法的不足．针对形状可调的参数曲线构造问题，本文提出了在三次Ferguson曲线、三次Bézier曲线、三次均匀B样条曲线等传统参数曲线中引入形状参数的方法，并将其定义区间由固定区间［0，1］扩展为动态区间［0，α］，在这些传统三次参数曲线中引入形状参数α，通过调节α的取值，实现对曲线形状的有效调整．

1 三次α－Ferguson曲线

1．1 三次α－Hermite基函数的构造

传统三次Ferguson曲线的基函数（也称为三次Hermite基函数）通常可表示为［15］

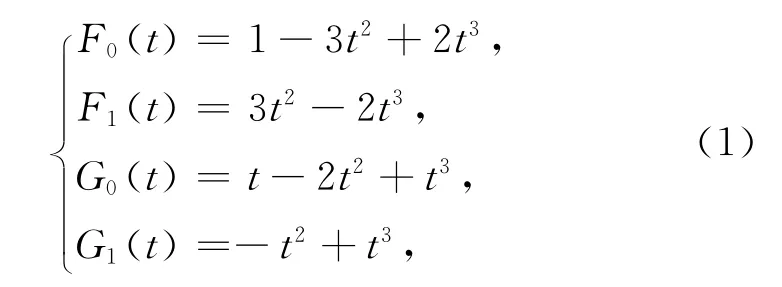
其中0≤t≤1．

由式（1）定义的传统三次Hermite基函数在端点处满足

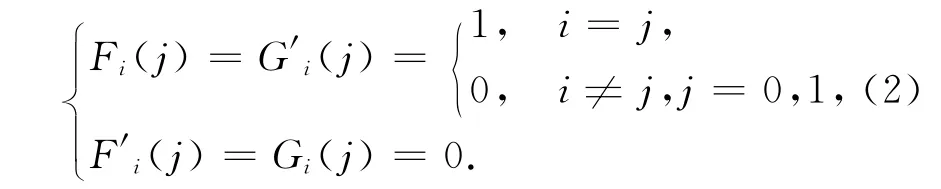
若将传统三次Hermite基函数的定义区间由t∈［0，1］扩展为动态区间t∈［0，α］（0＜α≤1），则可依据式（2）构造出一种带参数α的三次Hermite基函数．下面给出具体的构造过程．

设所要构造的4个新基函数为

其中，0≤t≤α，0＜α≤1，M为一待定的4×4矩阵．

式（3）两端对t求导得

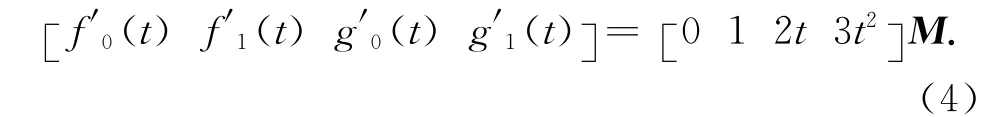
现要求新基函数具有传统三次Hermite基函数的端点性质，即满足式（2），有

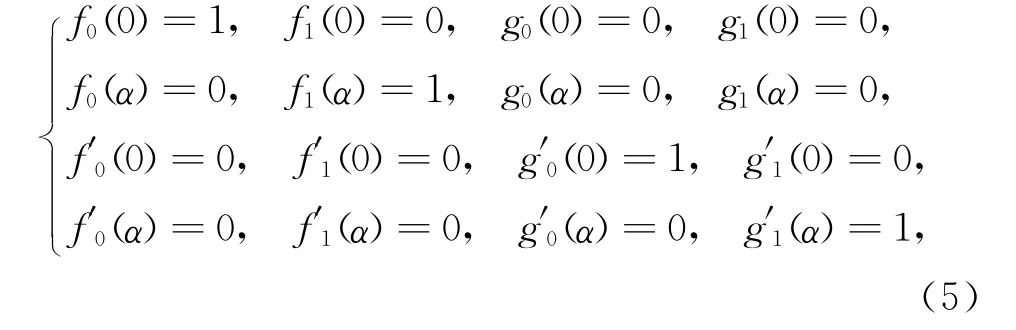
于是，将t＝0与t＝α分别代入式（3）和（4），可得

求解式（6）得

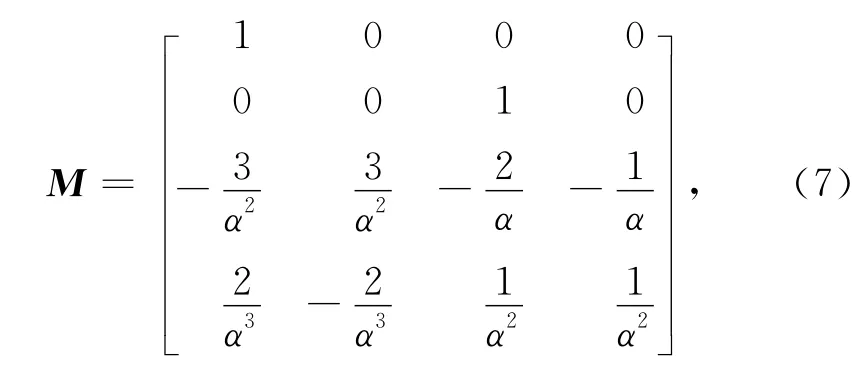
将式（7）代入式（3），可得所要构造的新基函数．

定义1 对于0≤t≤α，0＜α≤1，下列4个关于t的函数

称为带参数α的三次Hermite基函数，简称为三次α－Hermite基函数．

1．2 三次α－Ferguson曲线的定义及其性质

基于三次α－Hermite基函数，可定义如下带参数α的三次Ferguson曲线．

定义2 对于0≤t≤α，0＜α≤1，给定曲线段的首、末端点ai及其切矢a′i（i＝0，1），称曲线

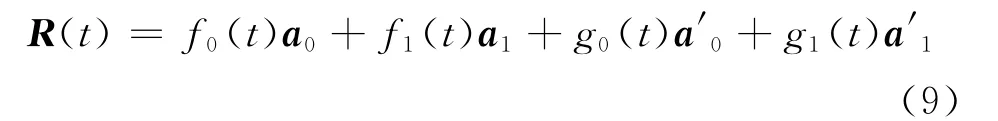
为带参数α的三次Ferguson曲线，简称为三次α－Ferguson曲线，其中fi（t）与gi（t）（i＝0，1）为式（8）定义的三次α－Hermite基函数．

由式（5）与（9），可得三次α－Ferguson曲线具有如下插值性：

定理1 由式（9）定义的三次α－Ferguson曲线插值于给定的首、末端点及其切矢，即

注1 定理1表明，三次α－Ferguson曲线与传统三次Ferguson曲线具有完全相同的插值性．特别地，当α＝1时，三次α－Ferguson曲线即为传统三次Ferguson曲线．因此，三次α－Ferguson曲线是传统三次Ferguson曲线的一种同次扩展．当曲线段的首、末端点及其切矢给定时，传统三次Ferguson曲线的形状无法修改，但三次α－Ferguson曲线的形状可通过修改参数α的值进行调节，从而为曲线的设计提供便利．

当曲线段的首、末端点及其切矢固定时，参数α对三次α－Ferguson曲线的形状有如下影响：

定理2 固定曲线段的首、末端点ai及其切矢ai′（i＝0，1），则参数α的取值越大，三次α－Ferguson曲线越远离边a0a1．

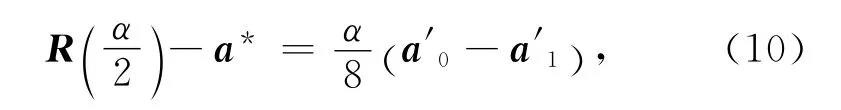
式（10）两边同时取范数有

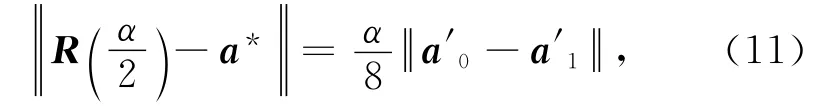
图1为曲线段的首、末端点及其切矢固定时参数α取不同值时的三次α－Ferguson曲线，图中各曲线由外到内所取的参数分别为a＝0．2，0．4，0．6，0．8，1．0．

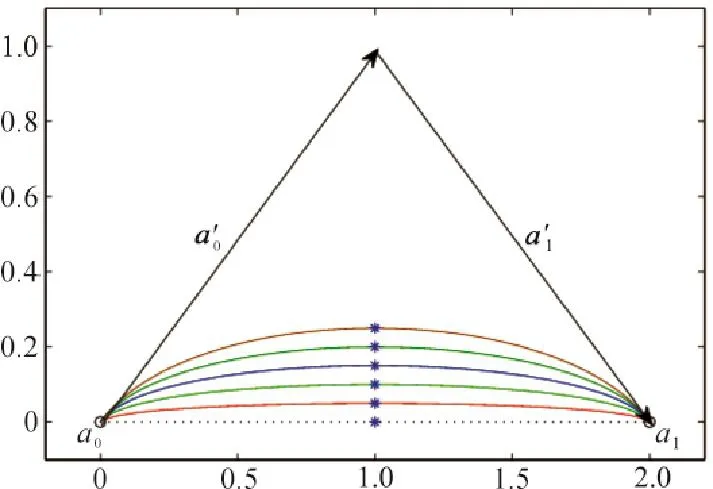
图1　参数α取不同值时的三次α－Ferguson曲线Fig．1 Cubicα－Ferguson curves with differentα

2 三次α－Bézier曲线

2．1 三次α－Bernstein基函数的构造

传统三次Bézier曲线的基函数（也称为三次Bernstein基函数）通常可表示为［15］

其中0≤t≤1．

由式（12）定义的传统三次Bernstein基函数在端点处满足：

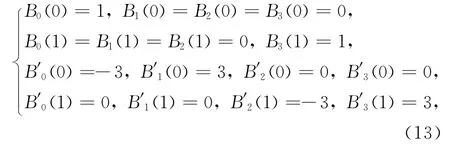
若将传统三次Bernstein基函数的定义区间由t∈［0，1］扩展为动态区间t∈［0，α］（0＜α≤1），则依据式（13）可构造出一种带参数α的三次Bernstein基函数．下面给出具体的构造过程．

设所要构造的4个新基函数为

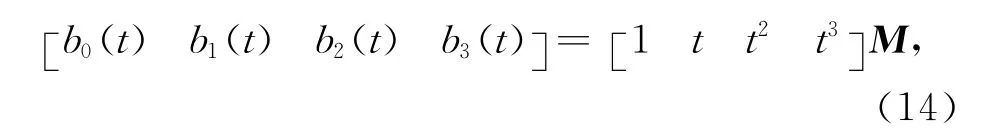
式中0≤t≤α，0＜α≤1，M为一待定的4×4矩阵．

式（14）两端对t求导得

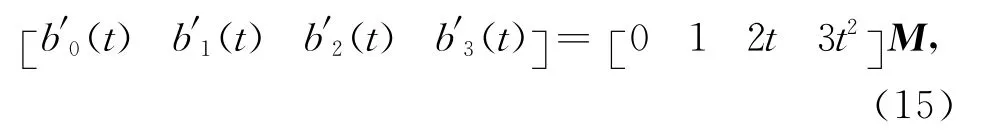
现要求新基函数具有传统三次Bernstein基函数的端点性质式（13），即有

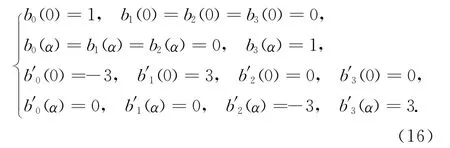
将t＝0与t＝α分别代入式14）和（15），可得

求解式（17），可得

将式（18）代入式（14），可得所要构造的新基函数．

定义3 对于0≤t≤α，0＜α≤1，下列关于t 的4个函数：

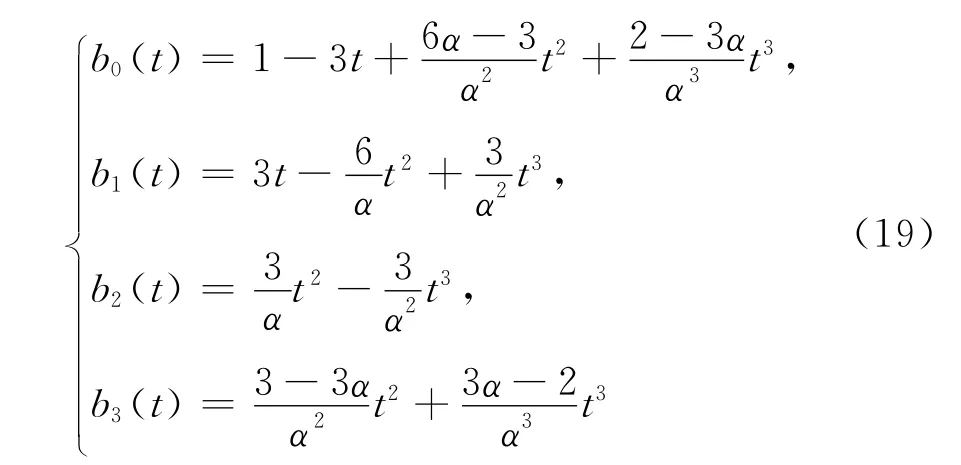
称为带参数α的三次Bernstein基函数，简称为三次α－Bernstein基函数．

定理3 由式（19）定义的三次α－Bernstein基函数具有如下性质：

（1）非负性：bi（t）≥0（i＝0，1，2，3）；

（2）混合性：b0（t）＋b1（t）＋b2（t）＋b3（t）≡1；

（3）对称性：bi（t）＝b3－i（α－t）（i＝0，1，2，3）；

（4）端点性质：三次α－Bernstein基函数在端点处满足式（16）．

证明 （1）式（19）可改写为

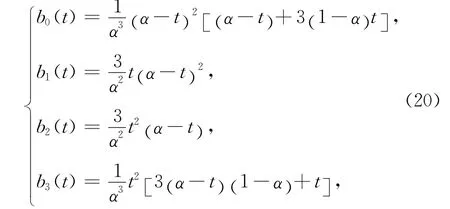
当0≤t≤α，0＜α≤1时，a－t≥0，1－α≥0．故由式（20）可得bi（t）≥0（i＝0，1，2，3）．

（2）由式（19）经简单计算可得混合性成立．

（3）由式（20）得对称性成立．

（4）由三次α－Bernstein基函数的构造可知，端点性显然成立．

2．2 三次α－Bézier曲线的定义及其性质

基于三次α－Bernstein基函数，可定义如下带参数α的三次Bézier曲线：

定义4 对于0≤t≤α，0＜α≤1，给定平面上或空间中4个控制顶点pi（i＝0，1，2，3），称曲线

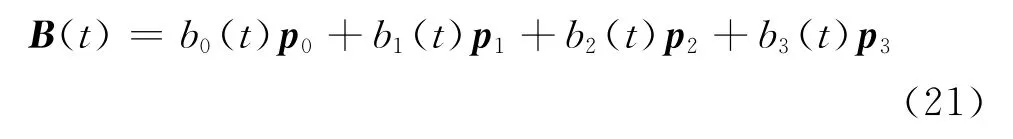
为带参数α的三次Bézier曲线，简称为三次α－Bézier曲线，其中bi（t）（i＝0，1，2，3）为式（19）定义的三次α－Bernstein基函数．

定理4 由式（21）定义的三次α－Bézier曲线具有如下性质：

（1）端点性质：三次α－Bézier曲线插值于首、末控制顶点，且与控制多边形的首、末边相切，即有

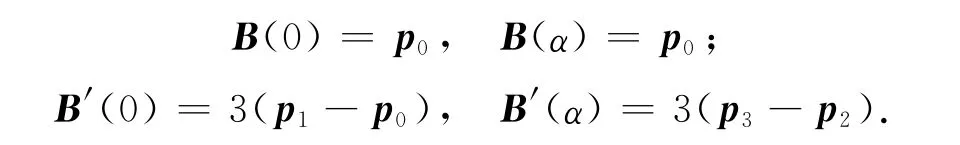
（2）对称性：对于相同的参数α，由控制顶点pi与p3－i（i＝0，1，2，3）分别确定的三次α－Bézier曲线重合，只是参数化方向相反，即有

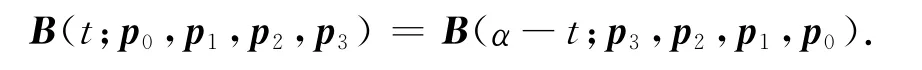
（3）几何不变性：三次α－Bézier曲线的形状和位置与坐标系的选取无关．

（4）凸包性与保凸性：三次α－Bézier曲线被完全包含在由控制顶点pi（i＝0，1，2，3）形成的凸包内．当控制多边形为凸时，三次α－Bézier曲线也为凸．

证明 （1）由式（16）与（21）可得

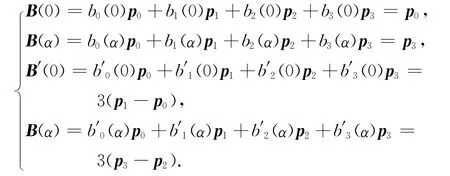
（2）由三次α－Bernstein基函数的对称性与式（21）可得

（3）由于式（21）为一矢量函数，故三次α－Bézier曲线的形状和位置与坐标系的选取无关．

（4）由于三次α－Bernstein基函数bi（t）（i＝0，1，2，3）满足非负性与权性，而式（21）是控制顶点pi关于bi（t）（i＝0，1，2，3）的加权线性组合，故三次α－Bézier曲线被完全包含在由控制顶点pi（i＝0，1，2，3）形成的凸包内．特别地，当控制多边形为凸时，三次α－Bézier曲线也为凸．

注2 定理4表明，三次α－Bézier曲线与传统三次Bézier曲线具有完全相同的性质．特别地，当α＝1时，三次α－Bézier曲线即为传统三次Bézier曲线．因此，三次α－Bézier曲线是传统三次Bézier曲线的同次扩展．当控制顶点保持不变时，传统三次Bézier曲线的形状无法修改，但三次α－Bézier曲线的形状可通过修改参数α的值进行调节，从而为曲线的设计提供了便利．

当控制顶点固定时，参数α对三次α－Bézier曲线的形状有如下影响．

定理5 设给定的控制顶点pi（i＝0，1，2，3）不共线，且p1与p2位于边p0p3的同侧，则参数α的取值越大，三次α－Bézier曲线越靠近控制多边形．

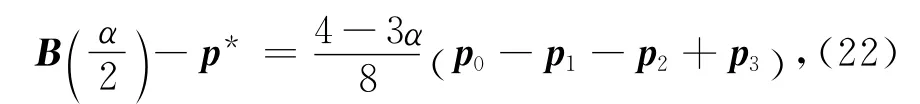
式（22）两边同时取范数有

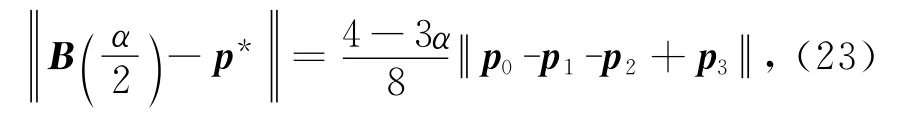
图2为控制顶点固定时，参数α取不同值时的三次α－Bézier曲线，图中各曲线由外到内所取的参数分别为α＝0．2，0．4，0．6，0．8，1．0．

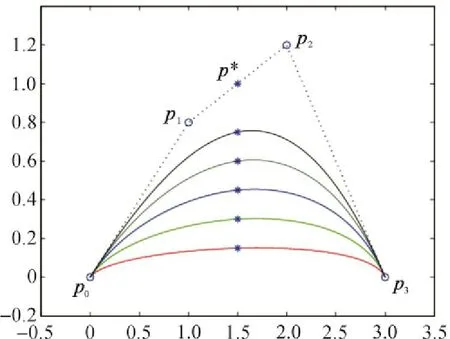
图2　参数α取不同值时的三次α－Bézier曲线Fig．2 Cubicα－Bézier curves with differentα

3 三次均匀α－B样条曲线

3．1 三次均匀α－B样条基函数的构造

传统三次均匀B样条基函数的表达式可写为［15］

其中，0≤t≤1．其在端点处满足

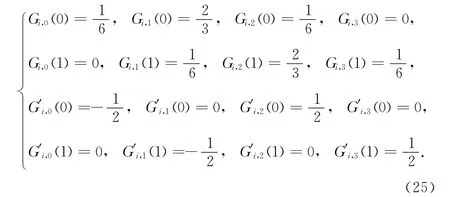
若将其定义区间由t∈［0，1］扩展为动态区间t∈［0，αi］（0＜αi≤1），则可依据式（25）构造出一种带参数的三次均匀B样条基函数．下面给出具体的构造过程．

设所要构造的新基函数为

式中0≤t≤αi，0＜αi≤1，M为一待定的4×4矩阵．

式（26）两端分别对t求导可得

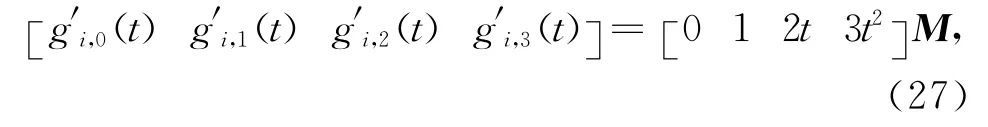
现要求新基函数具有传统三次Bernstein基函数的端点性质式（25），即满足

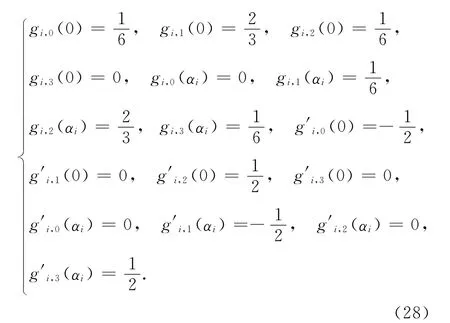
将t＝0与t＝αi分别代入式（26）与（27），则由式（28）可得

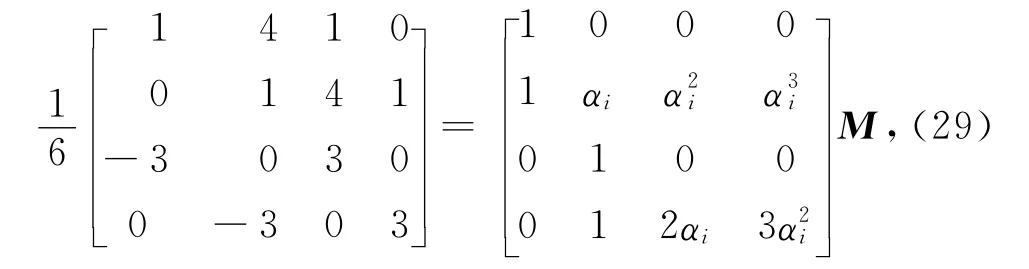
求解式（29）得

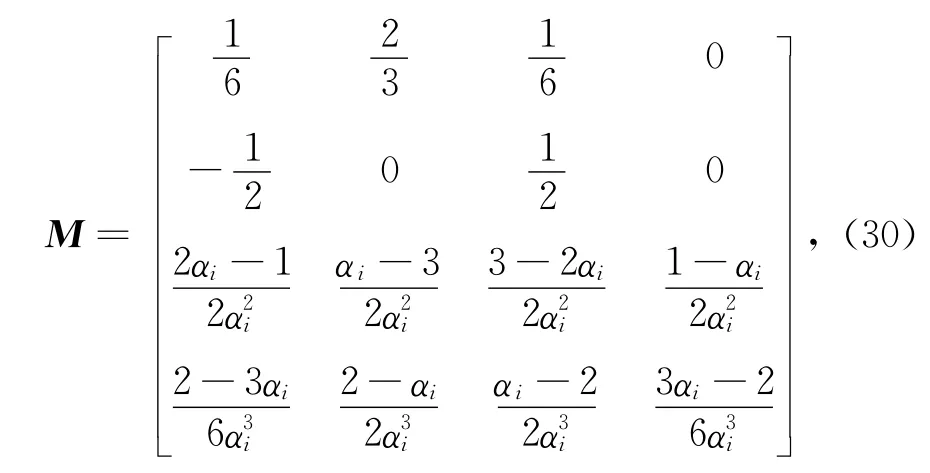
将式（30）代入式（26），可得所要构造的新基函数．

定义5 对于0≤t≤αi，0＜αi≤1，下列关于t的函数

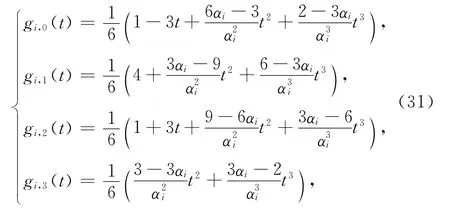
称为带参数αi的三次均匀B样条基函数，简称为三次均匀α－B样条基函数．

定理6 由式（31）定义的三次均匀α－B样条基函数具有如下性质：

（1）非负性：gi，j（t）≥0（j＝0，1，2，3）；

（2）混合性：

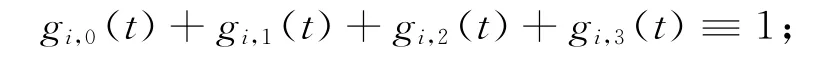
（3）对称性：

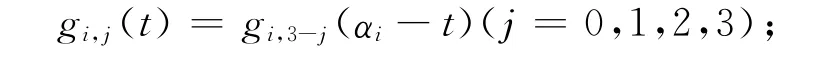
（4）端点性质：三次均匀α－B样条基函数在端点处满足式（26）；

（5）单调性：固定t∈［0，αi］（0＜αi≤1），g0（t）与g1（t）关于参数ai单调递减，g2（t）与g3（t）关于参数αi单调递减．

证明 （1）固定αi∈（0，1］，当0≤t≤αi时，由式（29）可得

故gi，0（t）与gi，1（t）关于变量t单调递减，gi，2（t）与gi，3（t）关于变量t单调递增，于是有

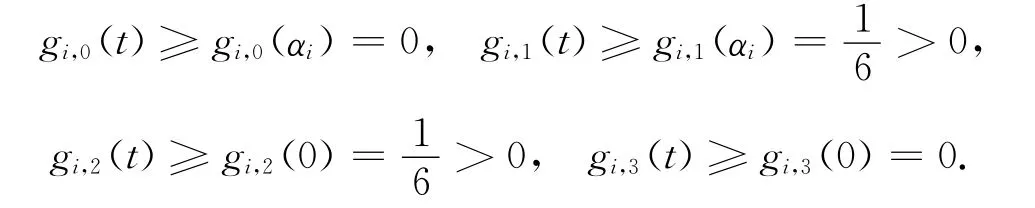
（2）由式（31）经简单推导，可得混合性成立．

（3）由式（31）经简单计算，可得对称性成立．

（4）由三次均匀α－B样条基函数的构造过程可知，端点性质显然成立．

（5）固定t∈［0，αi］（0＜αi≤1），由式（31）可得

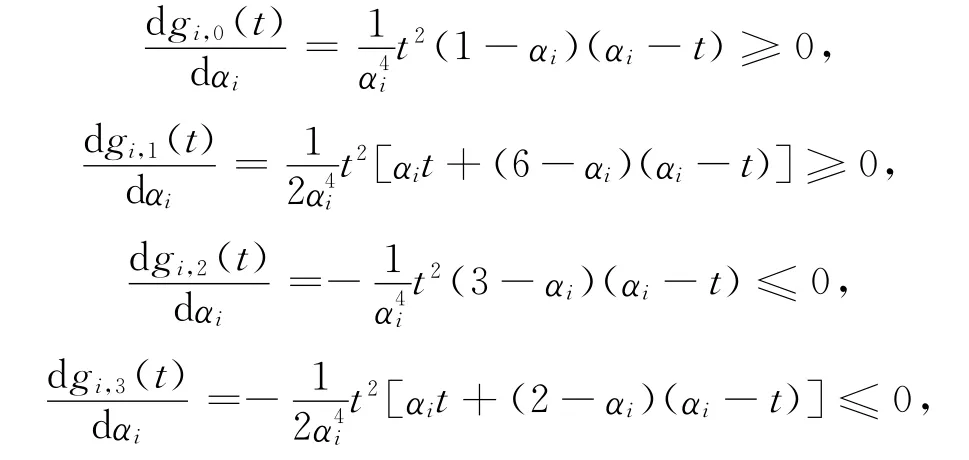
于是，gi，0（t）与gi，1（t）关于参数αi单调递增，gi，2（t）与gi，3（t）关于参数αi单调递减．

3．2 三次均匀α－B样条曲线的定义及其性质

基于三次均匀α－B样条基函数，可定义如下带参数αi的三次均匀B样条曲线：

定义6 对于0≤t≤αi，0＜αi≤1，给定平面上或空间中n＋1控制顶点qj（j＝0，1，2，…，n），称分段曲线

为带参数αi的三次均匀B样条曲线，简称为三次均匀α－B样条曲线，其中gi，j（t）（j＝0，1，2，3）为式（31）定义的三次均匀α－B样条基函数．

定理7 由式（32）定义的三次均匀α－B样条曲线具有如下性质：

（1）连续性：三次均匀α－B样条曲线满足C1连续，即满足

（2）对称性：对于相同的参数αi，分别由控制顶点确定的第i段三次均匀α－B样条曲线重合，只是参数化方向相反，即有

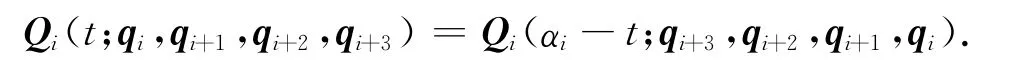
（3）几何不变性：三次均匀α－B样条曲线的形状和位置与坐标系的选取无关．

（4）凸包性与保凸性：第i段三次均匀α－B样条曲线被完全包含在由控制顶点qi＋j（j＝0，1，2，3）形成的凸包内．特别地，当所有控制顶点形成一个闭凸多边形时，三次均匀α－B样条曲线也为一条凸曲线．

证明 （1）由式（28）与（32）可得

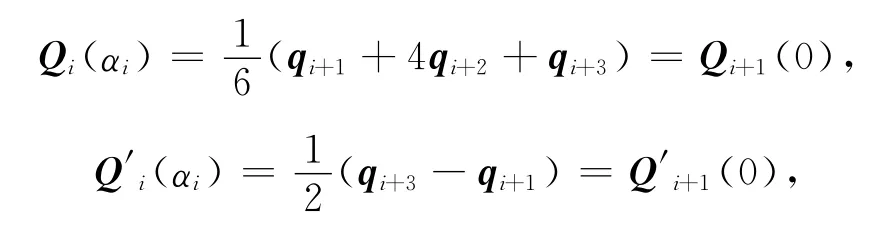
即三次均匀α－B样条曲线满足C1连续．

（2）由三次均匀α－B样条基函数的对称性与式（32）可得

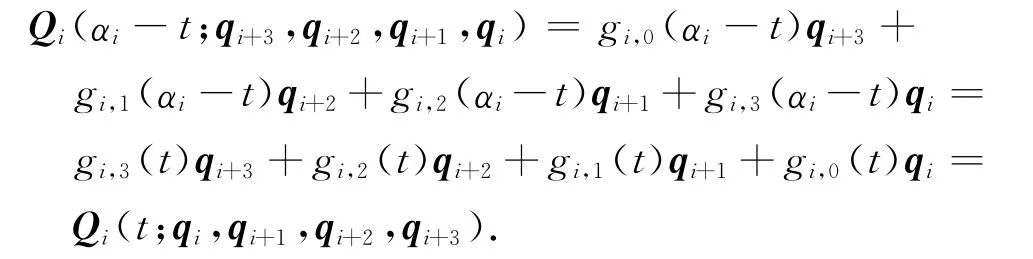
（3）由于式（32）为一矢量函数，故三次均匀α－B样条曲线的形状和位置与坐标系的选取无关．

（4）由于三次均匀α－B样条基函数gi，j（t）（j＝0，1，2，3）满足非负性与权性，而第i段三次均匀α－B样条曲线Qi（t）是控制顶点qi＋j关于gi，j（t）（j＝0，1，2，3）的加权线性组合，故第i段三次均匀α－B样条曲线被完全包含在由控制顶点qi＋j（j＝0，1，2，3）形成的凸包内．特别地，当所有控制顶点形成一个闭凸多边形时，三次均匀α－B样条曲线也为一条凸曲线．

注3 定理7表明，三次均匀α－B样条曲线与传统三次均匀B样条曲线具有几乎完全相同的性质（连续性除外，传统三次均匀B样条曲线满足C2连续）．特别地，当α＝1时，三次均匀α－B样条曲线即为传统三次均匀B样条曲线．因此，三次均匀α－B样条曲线是传统三次均匀B样条曲线的同次扩展．当所有控制顶点保持不变时，传统三次均匀B样条曲线的形状无法修改，但三次均匀α－B样条曲线的形状可通过修改参数α1的值进行调节，从而为曲线的设计提供了便利．

当所有控制顶点qj（j＝0，1，2，…，n）固定时，只修改参数α1的值，则只会对第i段三次均匀α－B样条曲线Qi（t）的形状有影响，而对其他曲线段无任何影响，即参数α1对整条三次均匀B样条曲线的形状具有局部调节作用．进一步，当第i段三次均匀α－B样条曲线的控制顶点qi＋j（j＝0，1，2，3）保持不变时，参数αi对曲线段的形状有如下影响：

定理8 设第i段三次均匀α－B样条曲线Qi（t）的控制顶点qi＋j（j＝0，1，2，3）不共线，且qi＋1与qi＋2位于边qiqi＋3的同侧，则参数α1的取值越大，曲线段越靠近其控制多边形．

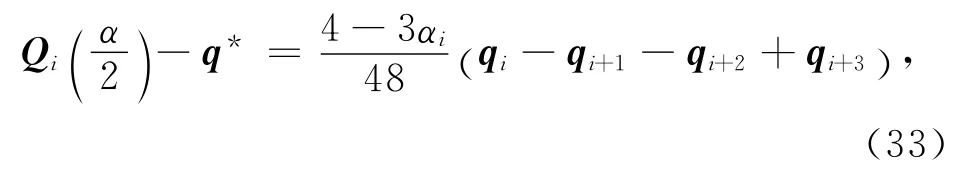
式（33）两边同时取范数有

由式（34）可知，参数αi取值越大的值越小，则越靠近q＊，即第i段三次均匀α－B样条曲线Qi（t）越靠近其控制多边形．

图3为当所有控制顶点固定时，参数αi对三次均匀α－B样条曲线的局部调节，图中第2段曲线由外到内参数α2＝0．3，0．6，0．9，其余各段曲线参数均为0．6．

图3　参数对三次均匀α－B样条曲线的局部调节Fig．3 Local adjustment of the parameter on a cubic uniformα－B－spline curve

当所有控制顶点qj（j＝0，1，2，…，n）固定时，若将所有三次均匀α－B样条曲线段Qi（t）（i＝0，1，2，…，n－3）的参数取为同一值α，即取αi＝α（i＝0，1，2，…，n－3），则可通过修改参数α的值实现对三次均匀α－B样条曲线的整体调节．图4为当所有控制顶点固定时，参数αi＝α（i＝0，1，2，3）对三次均匀α－B样条闭曲线的整体调节图，图中短虚线对应的参数α＝0．3，长虚线对应的参数α＝0．6，实线对应的参数α＝1．0．

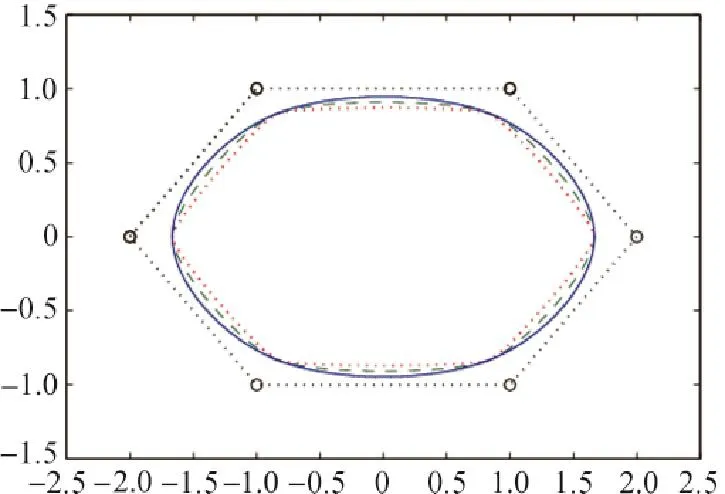
图4　参数对三次均匀α－B样条闭曲线的调节Fig．4 Global adjustment of the parameter on a closed cubic uniformα－B－spline curve

4 三次α－曲线之间的关系

三次α－Ferguson曲线的定义式式（9）可改写成矩阵形式：

式中0≤t≤α，0＜α≤1．

三次α－Bézier曲线的定义式式（21）可改写成矩阵形：

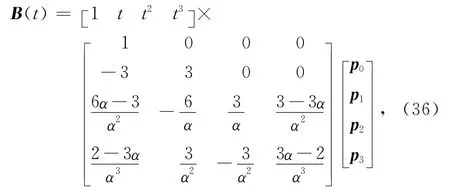
式中0≤t≤α，0＜α≤1．

若仅考虑一段曲线，则三次均匀α－B样条曲线的定义式式（32）可改写成矩阵形式：

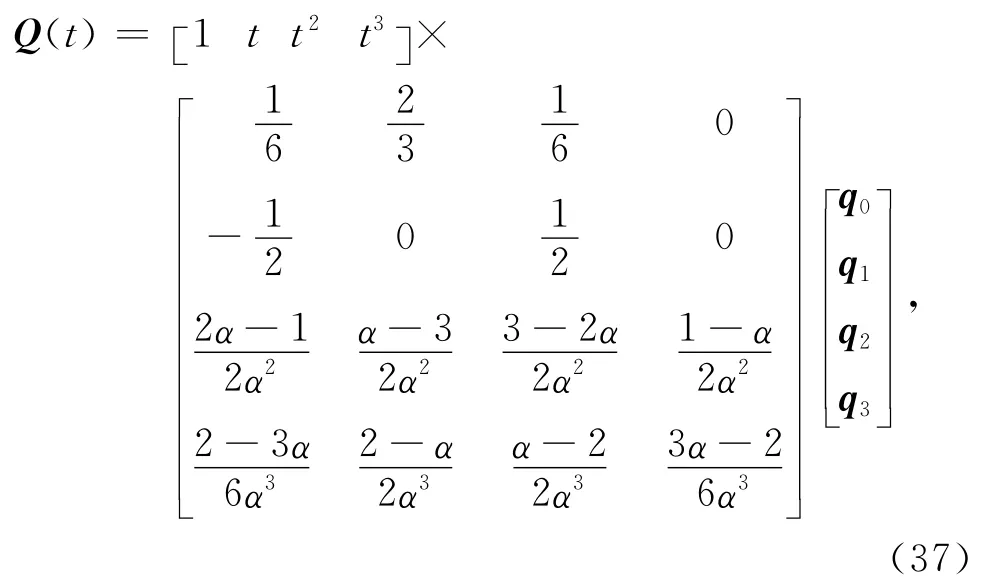
式中0≤t≤α，0＜α≤1．

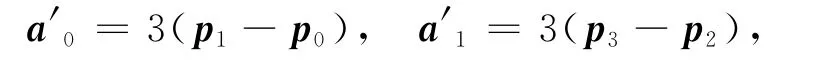
由式（35）与（36），三次α－Ferguson曲线可转化为三次α－Bézier曲线．

如果有

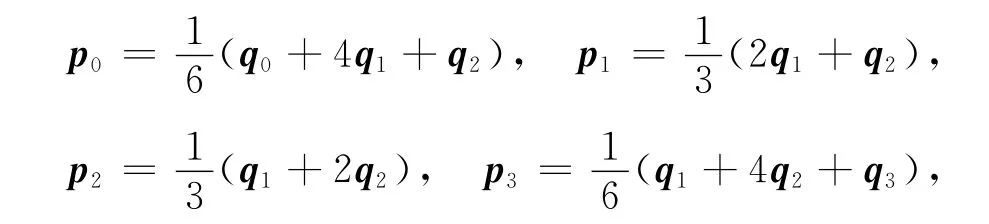
由式（36）与（37），则三次α－Bézier曲线可转化为三次均匀α－B样条曲线．

同样，如果有

则三次均匀α－B样条曲线可转化为三次α－Bézier曲线．

5 结 语

为了构造形状可调的参数曲线，将三次Ferguson曲线、三次Bézier曲线、三次均匀B样条曲线等传统参数曲线的定义区间由固定区间［0，1］扩展为动态区间［0，α］，构造了3种带参数α的三次曲线．所构造的新曲线不仅完全继承了传统三次参数曲线的性质，而且可通过修改参数α的值调整其形状．另外，所构造的新曲线均为多项式模型，且为相应三次参数曲线的同次扩展，相较其他类似的曲线模型，方程结构更简洁，因此是一种简单有效的带形状参数的曲线造型方法．目前众多CAD／CAM系统均采用了三次Ferguson曲线、三次Bézier曲线、三次均匀B样条曲线等参数曲线，本文所构造的新曲线与传统参数曲线的方程结构非常接近，因此可将其应用于相应的CAD／CAM系统中．进一步，可继续研究所构造的新曲线的具体算法，也可将所构造的新曲线推广到曲面形式，将另文讨论．

参考文献（References）：

［1］ YAN Lanlan，LIANG Qiongfeng．An extension of the Bézier model［J］．Applied Mathematics and Computation，2011，218（6）：2863－2879．

［2］ CHEN Jun，WANG Guojin．A new type of the generalized Bézier curves［J］．Applied Mathematics：A Journal of Chinese Universities，2011，26（1）：47－56．

［3］ CAO Juan，WANG Guozhao．Non－uniform B－splinecurves with multiple shape parameters［J］．Journal of Zhejiang U－niversity SCIENCE C，2011，12（10）：800－808．

［4］ FAN Feilong，ZENG Xiaoming．S－λbases and S－λcurves［J］．Computer－Aided Design，2012，44（11）：1049－1055．

［5］ QIN Xinqiang，HU Gang，ZHANG Nianjun，et al．A novel extension to the polynomial basis functions describing Bézier curves and surfaces of degree n with multiple shape parameters［J］．Applied Mathematics and Computation，2013，223：1－16．

［6］ LIU Xumin，XU Weixiang，GUAN Yong，et al．Hyperbolic polynomial uniform B－spline curves and surfaces with shape parameter［J］．Graphical Models，2010，72（1）：1－6．

［7］ YAN Lanlan，LIANG Jiongfeng．A class of algebraictrigonometric blended splines［J］．Journal of Computational and Applied Mathematics，2011，235（6）：1713－1729．

［8］ HAN Xuli，ZHU Yunpeng．Curve construction based on five trigonometric blending functions［J］．BIT Numerical Mathematics，2012，52（4）：953－979．

［9］ LI Juncheng．A class of cubic trigonometric Bézier curve with a shape parameter［J］．Journal of Information and Computational Science，2013，10（10）：3071－3078．

［10］ BASHIR U，ABBSA M，ALI J M．The G2and C2rational quadratic trigonometric Bézier curve with two shape parameters with applications［J］．Applied Mathematics and Computation，2013，219（20）：10183－10197．

［11］ PAPP I，HOFFMANN M．C2and G2continuous spline curves with shape parameters［J］．Journal for Geometry and Graphics，2007，11（2）：179－185．

［12］ XU Gang，WANG Guozhao．Extended cubic uniform B－spline andα－B－spline［J］．Acta Automatica Sinica，2008，34（8）：980－984．

［13］ JUHÁSZ I，HOFFMANN M．Surface interpolationwith local control by linear blending［J］．Annales

Mathematicae et Informaticae，2009，36（1）：77－84．

［14］ ZHU Yunpeng，HAN Xuli，HAN Jing．Quartic trigonometric Bézier curves and shape preserving interpolation curves［J］．Journal of Computational Information Systems，2012，8（2）：905－914．

［15］ 朱心雄．自由曲线曲面造型技术［M］．北京：科学出版社，2000．ZHU Xinxiong．Technology of Free Curves and Surfaces Modeling［M］．Beijing：Science Press，2000．

Interval extension of the cubic parametric curves

LI Juncheng，LIU Chengzhi（Department of Mathematics，Hunan University of Humanities，Science and Technology，Loudi 417000，Hunan Province，China）

Journal of Zhejiang University（Science Edition），2016，43（1）：079－086

Abstract：In order to introduce the shape parameter into the traditional cubic parametric curves，definition interval of cubic Ferguson curve，cubic Bézier curve and cubic uniform B－spline curve is extended from a fixed interval［0，1］to a dynamic interval［0，α］．Then three cubic parametric curves with parameterαare constructed，which are named cubicα－Ferguson curve，cubicα－Bézier curve and cubic uniformα－B－spline curve，respectively．The proposed threeα－curves are extensions of the corresponding cubic parametric curves．They not only have simple structure，inherit the properties of the corresponding cubic parametric curves，but also can be adjusted by altering the value of parameterα．Therefore，the proposed method is a simple and effective method for constructing shape－adjustable parametric curves．

Key Words：cubic parametric curves；interval extension；shape－adjustable

作者简介：李军成（1982－），男，博士，副教授，主要从事计算机辅助几何设计及其应用研究，E－mail：lijuncheng82＠126．com．

基金项目：湖南省教育厅资助科研项目（14B099）；湖南省自然科学基金资助项目（13JJ6081）．

收稿日期：2015－03－26．

DOI：10．3785／j．issn．1008－9497．2016．01．014

中图分类号：O 241．5；TP391

文献标志码：A

文章编号：1008－9497（2016）01－079－08