SHA-3算法的抗原象攻击性能优化
2016-05-14李建瑞汪鹏君张跃军宁波大学电路与系统研究所浙江宁波315211
李建瑞,汪鹏君,张跃军(宁波大学电路与系统研究所,浙江宁波315211)
SHA-3算法的抗原象攻击性能优化
李建瑞,汪鹏君*,张跃军
(宁波大学电路与系统研究所,浙江宁波315211)
摘 要:通过对SHA-3算法置换函数Keccak-f的线性性质以及缩减轮数的Keccak杂凑函数原象攻击的研究,提出了SHA-3算法的抗原象攻击性能优化设计方案.首先结合Keccak杂凑函数的差分特点和θ置换函数的奇偶性质,分析了基于CP-kernel的SHA-3算法原象攻击;然后针对目前实施原象攻击的方法,在θ置换函数运算后异或随机数以打乱其汉明重量,改变CP-kernel的校验性质,阻止攻击者利用中间相遇的方法寻找原象,提高了SHA-3算法的抗原象攻击能力;最后利用VHDL硬件语言实现抗原象攻击SHA-3算法的设计方案,验证了该算法的正确性以及安全性.
关 键 词:SHA-3算法;Keccak杂凑函数;抗原象攻击;随机数;安全性
Hash函数又称杂凑函数,被广泛应用于数字签名、消息认证、密码协议等,在密码学领域扮演着极其重要的角色.2007年,美国国家标准与技术研究所(National Institute of Standards and Technology,NIST)发布了一项公开征集活动,旨在推选密码学中散列函数的新标准——SHA-3算法.经过3轮筛选,2012年Keccak杂凑函数凭借其新颖的设计方法、较强的安全性能以及良好的实现方法成为新一代SHA-3算法[1].Keccak杂凑算法采用标准Sponge结构进行迭代,在软硬件平台上能够安全有效地实现,且能满足NIST对所提交算法的要求.同时NIST的计算机安全专家也对SHA-3算法的安全性能给予了高度评价[2],自此,Keccak作为一个新型杂凑函数登上了密码学的舞台.
由于SHA算法在密码学中的重要地位,新一代SHA算法的安全性引起了学者们的广泛关注,目前有关SHA-3标准Keccak算法的攻击方式主要有[3-8]:利用算法内部结构差分性质实施的碰撞攻击或部分碰撞攻击[3],其中对Keccak-256实施5轮碰撞攻击,复杂度为2115,同时结合squeeze规则对Keccak-512产生3轮的实际性攻击,对Keccak-384产生4轮的碰撞攻击,复杂度为2147;利用缩减轮数零和子集划分方式实施的区分攻击,其中对Keccak-512实施5轮的区分攻击,复杂度为212,并且提出针对全轮Keccak置换的零和划分[5];利用θ线性性质实施原像攻击,提出了Keccak-512版本3轮的实际性原象攻击和Keccak其他版本的4轮部分原像攻击[8],且时间复杂度要低于文献[7]中的2轮原象攻击.鉴于此,本文在研究SHA-3算法的差分性质以及θ置换函数的特点后,提出一种基于CP-kernel性质添加随机数的方法以提高SHA-3算法抗原象攻击的性能,同时该方案可抵御零和区分攻击.
1 SHA-3标准及零和区分性质
SHA-3标准Keccak算法是基于海绵构造(sponge construction)的Hash函数家族,将输入数据经过特殊的填充(pad)算法处理后的迭代杂凑函数定义为Keccak[r,c],其中,参数r表示比特率(bitrate),c表示容量(capacity),r+c决定Keccakf[b]杂凑函数中轮函数的置换宽度,即b=r+c,b∈{25,50,100,200,400,800,1600},Keccak算法所采用的sponge结构如图1所示,图中的f即为置换函数Keccak-f[b][1-2].
Keccak-f[b]为迭代置换函数,是Keccak算法的灵魂,迭代轮数nr由b决定:nr=12+2l,其中,2l=b/25,设计者最终提交的SHA-3标准Keccakf[b]轮函数的b值为1 600,则由此可得出具体的迭代轮数为24轮.Keccak杂凑函数在轮函数压缩处理时,每一轮的置换函数f都是作用在一个三维矩阵上的5步迭代置换,即R=τ。χ。π。ρ。θ,在三维矩阵中数据按照坐标轴x、y、z依次填充,运算过程中行元素记为a[.][y][z],列元素记为a[x][.][z],道元素记为a[x][y][.],对应关系为S[w(5y+x)]=A[x][y][z],w=b/25[2].
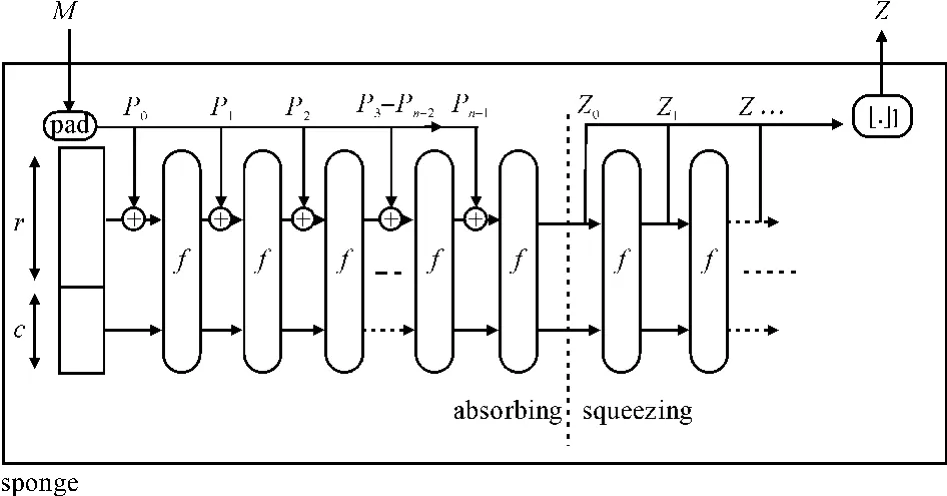
图1 Sponege结构Fig.1 Sponge construction
Keccak杂凑函数5个迭代环节中前4步是在三维矩阵中进行不同方向的行、列、道以及面的变换,从而达到混淆和扩散三维数组的目的,最后一步置换是在三维数组的第1道上异或一组轮常数,以破坏原有的对称性.其中,在x和y轴上是模“5”运算,而在z轴上是模“w”运算,具体的5步置换函数式如下[]:

SHA-3算法原象攻击的基本定义为:对给定的输入消息值M,经算法运算后很容易计算出摘要值H(M),根据H(M),也可计算出消息值M或部分M值.这违反了杂凑函数的单向性原则,攻击者可对SHA-3算法实施有效的原象攻击.
SHA-3算法的零和区分性质由AUMASSON[7]首先提出,其基本定义为:令F是一个从到的函数,长度为k的零和输入子集经函数F运算后结果仍然为零,定义如式(1)所示:
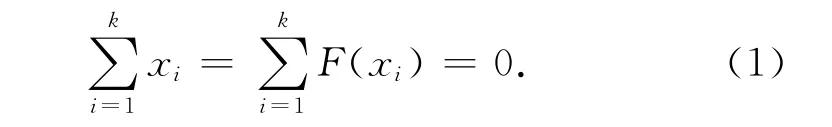
攻击者通过零和区分性质利用零和区分器可以找出零和子集,从而对SHA-3算法实施缩减轮数的区分攻击.
2 抗原象攻击SHA-3算法优化
2.1 SHA-3算法的θ置换函数
Keccak算法5步迭代中θ函数是比特级的按位异或运算过程,作用在整个三维数组中,具有很好的扩散性质,A[x][y][z]的更新值可表示为A[x][y][z]与2列之和做按位异或运算,2列即:A[x-1][.][z]和A[x+1][.][z-1],θ的数学模型如图2所示.从而可以得出三维矩阵中θ函数所有的列具有奇偶校验性质,假设三维数组中的某一列有2个活性位,经θ函数变换后,活性位的个数不变,仅改变位置,将这种状态集称为列校验内核(Column parity kernel)或者CP-kernel[1,8].

图2 θ置换函数的数学模型Fig.2 Mathematical model ofθpermutation function
2.2 CP-kernel原象攻击
文献[8]提出利用迭代函数θ的奇偶性质对SHA-3算法实施4轮的原象攻击,其中一种方法是在1 600位宽的状态矩阵中每一列和为0时,θ运算不会引起差分改变,其汉明重量也不变,实施攻击过程中设计者从具有最低汉明重量的CP-kernel差分性质开始,通过1轮运算仍然保持一个非常低的汉明重量;第2种攻击方法是利用简单的观察法,经θ运算更新的一列位元的5位值要么保持不变,要么全部翻转,所以在攻击过程中即使不清楚所给列的每一个位元,只需将选择的位元经过θ运算便可看出该位元的变化,具体分析如图3所示.
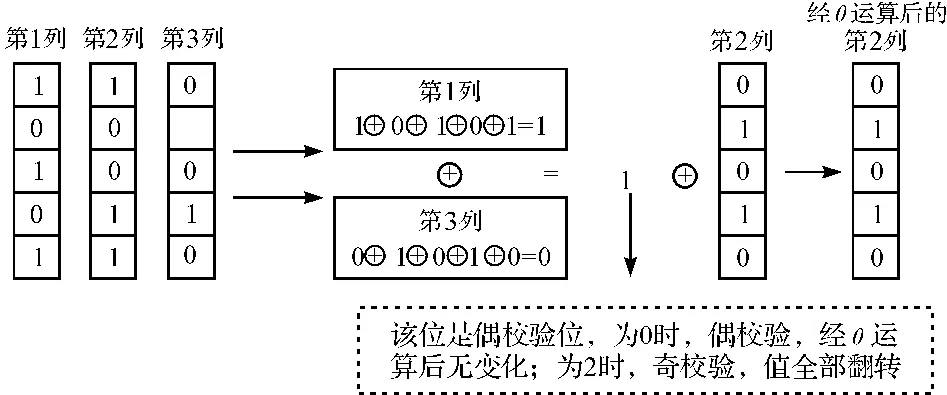
图3 θ置换函数的列校验性质Fig.3 Column parity kernel property of θpermutation function
θ置换函数中所有运算均基于列的异或,如果θ状态矩阵中每一列均具有偶校验性质,则1 600位状态差异存在于CP-kernel中,且状态差异经函数θ运算后保持不变;如果有一列奇数位存在差异,则经过θ运算后可将其扩展到10位,所以θ函数在5步迭代中起到扩散三维数组的作用.正因为θ具有列奇偶校验的性质,攻击者可利用该性质对SHA-3算法实施缩减轮数的原象攻击、碰撞攻击以及近似碰撞攻击.所以θ置换函数运算后的异或随机数,其目的就是破坏原有的奇偶性,攻击者即使分析出中间状态每一列的奇偶性,但进入ρ的初始状态后,无法在后续步骤中应用θ性质进行攻击.
2.3 CP-kernel抗原象攻击的改进
SHA-3算法5步迭代置换中的θ函数具有CP-kernel性质,利用该性质寻找差分路径[9],从而可采用中间相遇的方法对缩减轮数的SHA-3算法进行攻击.首先,结合文献[8]和[10]对SHA-3算法成功实施了3轮原象攻击、2轮碰撞攻击以及3轮近似碰撞攻击.然后,根据SHA-3算法θ函数的CP-kernel性质,每一轮置换函数经θ运算后,所得结果与随机数做异或运算,即R=θ⊕γ。ρ。π。χ。τ,打乱经θ置换函数运算后的汉明重量,针对3轮的原象攻击方法,提出了一种基于随机数的增强型CP-kernel抗原象攻击方案,见图4.
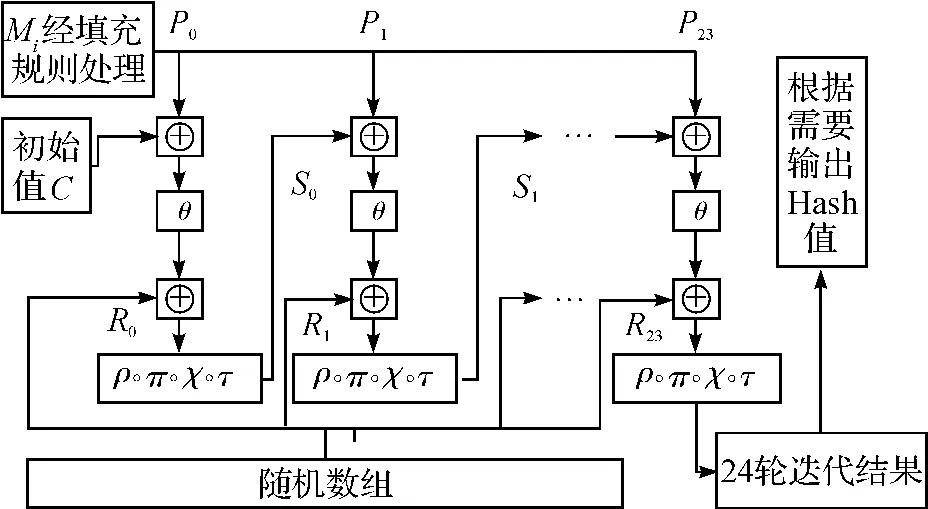
图4 增强型CP-kernel抗原象攻击方案Fig.4 Preimage resistance attack based on the improved CP-kernel
图4给出了对SHA-3算法实施抗原象攻击的具体运算过程,其中,Mi代表需要处理的消息值,C代表初始状态中的容量值,Si代表每一轮迭代运算后的中间链值,Ri则表示输入的随机数,每轮加入的随机数视使用者对开销面积的要求而定,可以是相同的一组数据,也可以是不同的数据.Mi经过一轮改进的置换函数运算后,其中间值与逆运算得到的中间值是一样的,在迭代函数θ后异或了随机数,由于缩减轮数的原消息值在迭代过程中异或未知的随机数,导致即使中间结果相同,反推出的信息值与原信息值却不相等,所以该方法可阻止利用中间相遇的方法寻找原象,提高了SHA-3算法的安全性.此外,在θ置换函数运算后异或随机数,可以阻止现有的区分器找到缩减轮数的SHA-3算法零和子集路径,从而使攻击者在知道杂凑值的情况下,无法利用现有的方法对SHA-3算法进行原象攻击.
2.4 SHA-3算法抗原象攻击优化
在SHA-3算法5步迭代θ函数后异或随机数,对算法原有的CP-kernel进行改进,改变每轮θ函数的奇偶性,阻止攻击者利用该限制条件实施攻击.SHA-3算法抗原象攻击优化结构如图5所示,该设计结构主要包含总控制端、数据的缓存、轮函数和数据读写4个模块,其中总控制端主要是保证各个模块按照算法流程工作;数据缓存(buffer)主要是为避免运算过程中内部数据处理速度低于外部数据读取速度导致输入信息覆盖而增加的一个缓存模块;轮函数是算法结构的核心,是根据算法的安全性需要所设计的24轮5步迭代置换函数,随机数添加在θ函数运算后的状态矩阵中,提高了算法的安全性;数据读写模块主要根据要处理的消息值以及所需杂凑值长度,按照规定进行数据的读写.算法本身的处理速度主要体现在24轮5步迭代的过程中,所以硬件语言以速度优先的方法实现,在一个时钟周期内完成5步迭代运算.
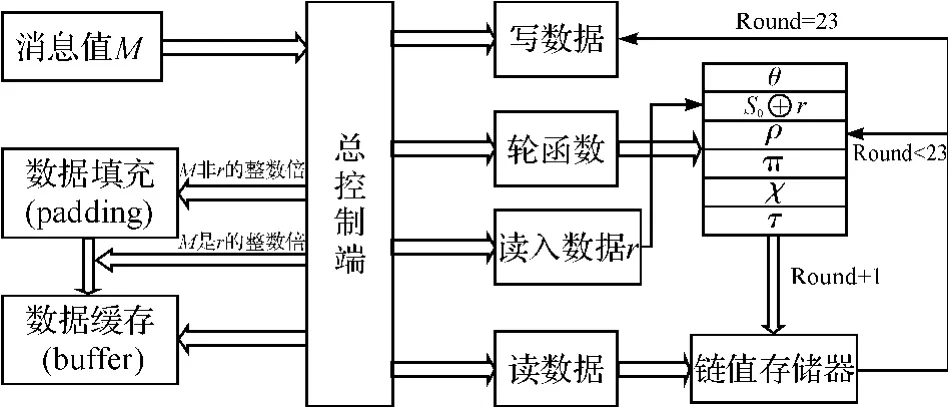
图5 SHA-3算法抗原象攻击性能优化设计框图Fig.5 The block of optimization preimage resistance on SHA-3algorithm
该设计利用VHDL硬件语言实现,首先用matlab产生一组随机数并且将该组数据存储在相应的寄存器中,经θ函数迭代运算后,将随机数与更新后的状态矩阵进行异或运算.算法伪代码如下:
Algorithmθ
Random—R[x]
for x=0to 4do
C[x]=a[x,0]
for y=1to 4do
C[x]=C[x]⊕a[x,y]
end for
end for
for x=0to 4do
D[x]=C[x-1]⊕ROT(C[x+1],1)
for y=0to 4do
B[x,y]=a[x,y]⊕D[x]
A[x,y]=B[x,y]⊕R[x]
end for
end for
3 实验结果与分析
根据SHA-3算法所提供的KAT(Knowledge acquisition toolkit)数据,对所提出的SHA-3算法抗原象攻击方案进行多组数据测试与分析,加入随机数后,θ在进入下一步迭代函数的列奇偶校验性质变为未知,所以采用中间相遇的方法无法对SHA-3实施有效的原象攻击和碰撞攻击,测试版本选择Keccak-256[11-12].
表1是Keccak算法的输入消息值,其中CaV 是Capacity Value的缩写,表示容量值,在每轮的迭代过程中长度是固定的;表2是θ置换函数输出后异或的随机数,其中ChV是Chaining Value的缩写,表示每轮迭代在5步函数运算后的结果,其长度为三维数组的大小.表3与4是算法前4轮中的256位部分输出结果,S下标代表轮数,其中表3为由表1中的输入数据经过SHA-3算法后的部分输出值,表4为在本文方案的基础上,加入随机数后SHA-3标准部分的输出值.由于对应道上二者的输出值完全不同,在θ之后加入未知的随机数,则无法通过中间相遇的方法推算出每轮状态的初始值,改变CP-kernel的奇偶校验特性,从而有效抵御攻击者利用θ性质以及中间相遇的方法对SHA-3实施原象攻击.

表1 输入数据Table 1 Input data

表2 输入随机数Table 2 Input random data
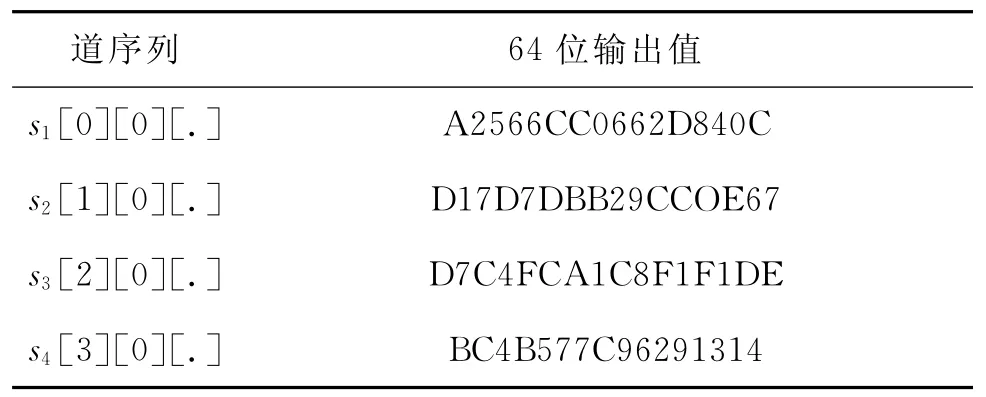
表3 SHA-3标准输出结果Table 3 Standard output results of SHA-3

表4 SHA-3改进后的输出结果Table 4 Output results of improved SHA-3
基于随机数提出的抗攻击方案,增加了寻找零和子集的复杂度[13-14],消息值或者经每一轮运算后中间链值的零和子集经过5步迭代运算后结果不为零;或者消息值和中间链值子集不为零,经5步迭代运算后其结果为零.表5与6是SHA-3算法最终的Hash值,以下就输出结果做几组分析:第1组:当表1中输入数据“010F1”为零和子集时,表5中对应位的输出“C3E01”为零和子集,表6中对应位的输出“459BD”子集之和不为零,可以记为“001”;第2组:“00000”“4E142”“AA1C6”,可记为“001”;第3组:“0000000”“30E0F041”“18E4D3A”,可记为“001”.从输入输出数据可看出,加入随机数后零和子集的排列发生了改变,而且每一轮同一状态下零和子集的分布也不同,因此攻击者无法准确找出初始值对应的零和子集,并对SHA-3算法实施零和区分攻击.
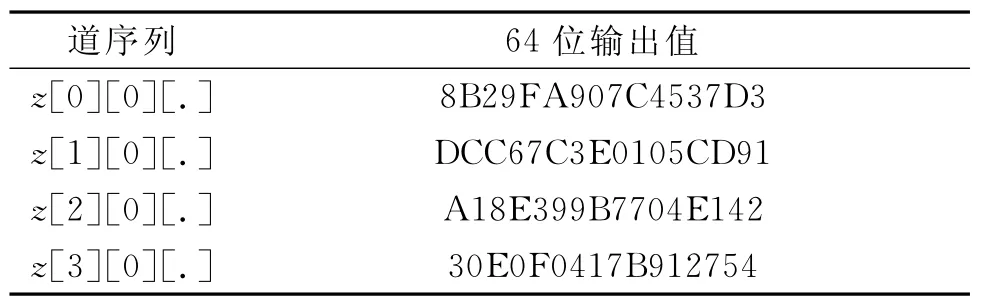
表5 SHA-3标准输出结果Table 5 Standard output results of SHA-3

表6 SHA-3改进后的输出结果Table 6 Output results of improved SHA-3
4 结 论
通过对SHA-3算法的加密过程以及性质的研究,并结合θ置换函数的CP-kernel性质,基于目前对SHA-3算法实施原象攻击所使用的方法,提出了一种有效的抗原象攻击方案,并利用硬件语言实现了此方案.实验结果表明,该设计使得SHA-3算法具有良好的加密特性,在不改变算法新颖独特的海绵结构设计的同时,增加了寻找零和子集的复杂度,可抵御零和区分攻击,具有良好的抗原象攻击能力,进一步提高了算法的安全性能,拓宽了SHA-3算法的应用范围.
参考文献(References):
[1] BERTONI G,DAEMEN J,PEETERS,M,et al.The Keccak[J].Lecture Notes in Computer Science,2013,7881:313-314.
[2] BERTONI G J,DAEMEN J,PEETERS M,et al.Cryptographic sponge functions,January,2011,http://sponge.noekeon.org.
[3] DINUR I,DUNKELMAN O,SHAMIR A.New attacks on Keccak-224and Keccak-256[C]//Fast Software Encryption.Heidelberg:Springer,2012:442-461.
[4] DINUR I,DUNKELMAN O,SHAMIR A.Collision attacks on up to 5rounds of SHA-3using generalized internal differentials[C]//Fast Software Encryption.Heidelberg:Springer,2014:219-240.
[5] DUAN M,LAI X J.Improved zero-sum distinguisherfor full round Keccak-f permutation[J].Chinese Science Bulletin,2012,57(6):694-697.
[6] NAYA-PLASENCIA M,RÖCK A,MEIER W.Practical Analysis of Reduced-Round Keccak[M].Heidelberg:Springer,2011:236-254.
[7] AUMASSON J P,MEIER W.Zero-sum distinguishers for reduced Keccak-fand for the core functions of Luffa and Hamsi[C].ACM Conference on Computer &Communications Security,Chicago:ACM,2009:1-4.
[8] MORAWIECKI P,PIEPRZYK J,SREBRNY M,et al.Preimage attacks on the round-reduced Keccak with the aid of differential cryptanalysis[J].Eprint Iacr Org,2013:2003:561.
[9] MORAWIECKI P,PIEPRZYK J,SREBRNY M.Rotational cryptanalysis of round-reduced Keccak[C]//Fast Software Encryption.Heidelberg:Springer,2014:241-262.
[10] NAYA-PLASENCIA M,ROCK A,MEIER W.Practical analysis of reduced-round keccak.In:Bernstein[C]//The 2011International Conference on Cryptology.India:Springer,2011(12):236-254.
[11] 高晓东,杨亚涛,李子臣.SHA-3置换函数的差分转移概率分析[J].计算机科学,2014,41(3):159-162.GAO Xiaodong,YANG Yatao,LI Zichen.Differential transition probability analysis of SHA-3permuta-tion function.Computer Science,2014,41(3):159-162.
[12] BAYAT-SARMADI S,MOZAFFARI-KERMANI M,REYHANI-MASOLEH A.Efficient and concurrent reliable realization of the secure cryptographic SHA-3algorithm[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2014,33(7):1105-1109.
[13] TAHA M,SCHAUMONT P.Side-channel countermeasure for SHA-3at almost-zero area overhead[C]//2014IEEE International Symposium on Hardware-Oriented Security and Trust(HOST).Arlington:IEEE,2014:93-96.
[14] LI Jianrui,WANG Pengjun,JIANG Zhidi,et al.Design of anti-distinguish attack of SHA-3algorithm based on enhancement-mode CP-Kerne![C]//2014 IEEE 12th International Conference on Solid State and Integrated Circuit Technology Proceedings.Guilin:ICSICT 2014,2014.
Optimization of preimage resistance on SHA-3algorithm
LI Jianrui,WANG Pengjun,ZHANG Yuejun(Institute of Circuits and System,Ningbo University,Ningbo 315211,Zhejiang Province,China)
ournal of Zhejiang University(Science Edition),2016,43(1):097-102
Abstract:By analyzing the linear property of Keccak-fpermutation functions of SHA-3algorithm and the round-reduced preimage attack of Keccak hash function,an optimization of preimage resistance on SHA-3algorithm is proposed.Firstly,we combine the differential property of Keccak algorithm and even parity ofθpermutation function,and analyze the preimage resistance of SHA-3algorithm based on CP-kernel.Secondly,according to the current preimage attack methods on SHA-3algorithm,the output ofθpermutation function XOR random numbers are used to change Hamming weight and to improve the properties of CP-kernel.It prevents an attacker from using meet-in-themiddle method to find the preimage.Finally,the scheme has been implemented with VHDL hardware language.And,the results show that the encryption process has a good performance and high security.
Key Words:SHA-3algorithm;Keccak hash function;preimage resistance;random numbers;security
通信作者*,E-mail:wangpengjun@nbu.edu.cn.J
作者简介:李建瑞(1989-),女,硕士,主要从事低功耗集成电路和信息安全芯片理论研究及设计.
基金项目:国家自然科学基金资助项目(61274132,61474068);浙江省自然科学基金资助项目(LQ14F04001).
收稿日期:2015-02-04.
DOI:10.3785/j.issn.1008-9497.2016.01.016
中图分类号:TN 79
文献标志码:A
文章编号:1008-9497(2016)01-097-06
