关于Lipschitz拟伪压缩映像族的强收敛定理

高兴慧，杨春萍（延安大学数学与计算机科学学院，陕西延安716000）



关于Lipschitz拟伪压缩映像族的强收敛定理

高兴慧，杨春萍
（延安大学数学与计算机科学学院，陕西延安716000）

摘 要：在Hilbert空间中设计出2种新的关于Lipschitz拟伪压缩映像族和严格拟伪压缩映像族的收缩投影算法，并利用所提出的算法证明了Lipschitz拟伪压缩映像族和严格拟伪压缩映像族的公共不动点的强收敛定理，所得结果改进和推广了已有文献的相关结果．

关 键 词：收缩投影算法；Lipschitz拟伪压缩映像族；公共不动点

在无限维Hilbert空间中，即使对于非扩张映像来说，正规Mann迭代格式一般也仅有弱收敛定理，为了得到强收敛定理，须改进Mann迭代格式．通过修正正规Mann迭代算法，使得对于非扩张映像、严格伪压缩映像和伪压缩映像的强收敛定理能够成立，这些结果可参见文献［1－12］．文献［1］在Hilbert空间中给出了几种修正的混杂投影算法，用以逼近严格拟伪压缩映像族和Lipschitz拟伪压缩映像族的公共不动点，这些结果改进和推广了文献［2，4，6］的相关结果．另外，文献［3］设计了固定非扩张映像和非扩张映像的收缩投影方法．受文献［1，3］的启示，在Hilbert空间框架下，设计了2种关于Lipschitz拟伪压缩映像族和严格拟伪压缩映像族的收缩投影算法，并证明其公共不动点的强收敛定理，所得结果改进和推广了文献［1－4，6－7］的相关结果．

1 预备知识

定义1 如果

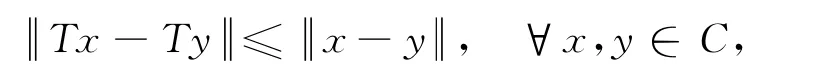
则称映像T：C→H是非扩张映像．

定义2 如果存在常数κ∈［0，1），使得

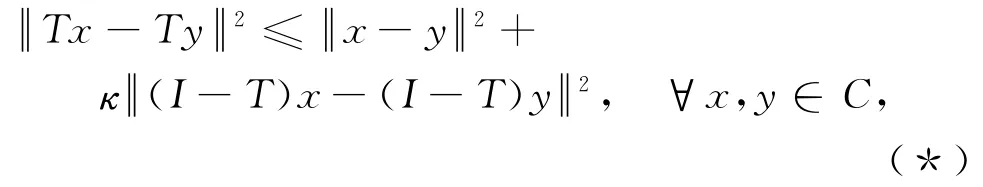
则称映像T：C→H是严格伪压缩映像，也称T是κ－严格伪压缩映像．

非扩张映像是特殊的严格伪压缩映像，即T是非扩张映像，当且仅当T是0－严格伪压缩映像．

定义3 如果存在一个常数L，使得

则称映像T：C→H是Lipschitz映像，也称T是L－Lipschitz映像．

严格伪压缩映像是Lipschitz伪压缩映像，其逆不真［1］．

定义4 如果F（T）≠Ø，且对于任意的x∈C，y∈F（T），式（＊）成立，则称映像T：C→H是严格拟伪压缩映像．当κ＝1时，称T为拟伪压缩映像；当κ＝0时，称T为拟非扩张映像．

显然，不动点集非空的伪压缩映像是拟伪压缩映像，反之不真．

例1［2］设

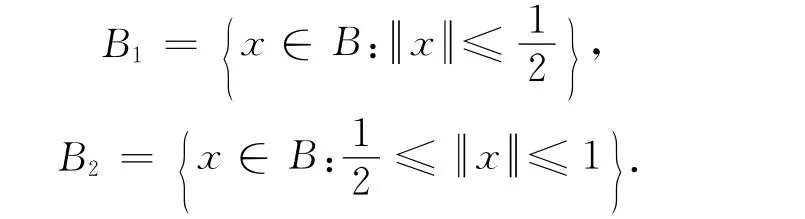
则T是Lipschitz伪压缩映像，但不是严格伪压缩映像．

例2［2］设X＝R1，定义

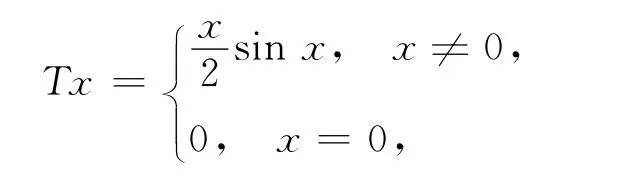
则T是拟伪压缩映像，但不是伪压缩映像．

设｛Tn｝是C到H的映像族，且｛Tn｝满足条件如果｛xn｝是C中的有界序列，且则（详见文献［3］，这里ωω（xn）表示｛xn｝的弱极限集）．

例3［3］设H是Hilbert空间，A⊂H×H是极大单调算子，且A－10≠Ø，｛rn｝是有界正实数序列，则预解式满足条件（Z），这里

例4［3］设H是Hilbert空间，C是H的非空闭凸子集，｛Sn｝：C→C是强非扩张映像族，使得．令，则｛Tn｝满足条件（Z）．

引理1［1］设H是Hilbert空间，C是H的非空闭凸子集，T是C到H的Lipschitz拟伪压缩映像，其Lipschitz常数为L≥1，则F（T）是C的非空闭凸子集．

引理2［4］设H是Hilbert空间，C是H的非空闭凸子集，PC：H→C是H到C的度量投影，则下列不等式成立：

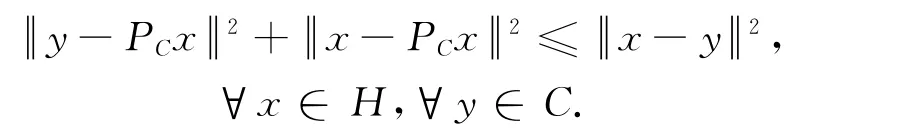
引理3［4］设H是Hilbert空间，则下列等式成立：

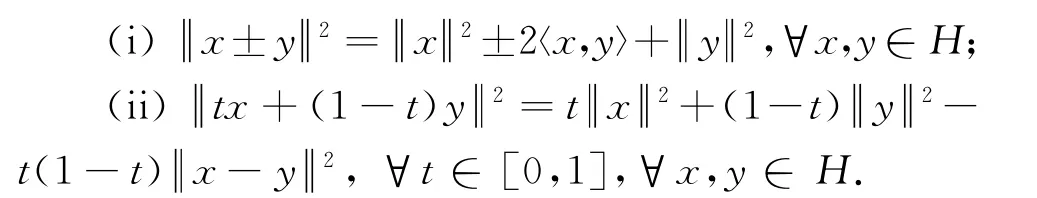
引理4［4］设H是Hilbert空间，C是H的非空闭凸子集，T：C→H是κ－严格拟伪压缩映像，则F（T）是C的非空闭凸子集．

2 主要结果

定理1 设H是Hilbert空间，C是H的非空闭凸子集，｛Tn｝：C→H是Ln－Lipschitz拟伪压缩映像族，使得．假设，且｛αn｝，｛βn｝满足下列条件：

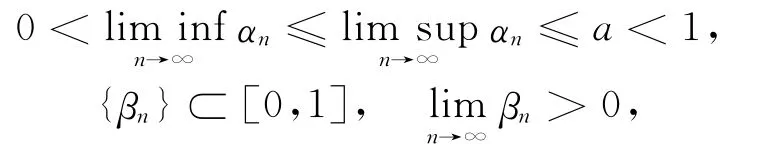
｛xn｝如下：

如果｛Tn｝满足条件（Z），那么｛xn｝强收敛于PFx．

证明 分6步完成证明．

第1步 证明对任意x∈H，PFx都有意义．

由引理1可知，对于任意n∈N，F（Tn）是C的非空闭凸子集，根据定理的条件可得是C的非空闭凸子集，从而对于任意x∈H，PFx都有意义．

第2步 证明对任意n∈N，Cn是C的非空闭凸子集．

显然，对于任意n∈N，Cn是C的闭凸子集．下面证明F⊂Cn，∀n∈N．事实上，F⊂C＝C1．假设对某一n∈N，F⊂Cn，由式（1）以及Tn的Ln－Lipschitz连续性可得，对任意的p∈F，

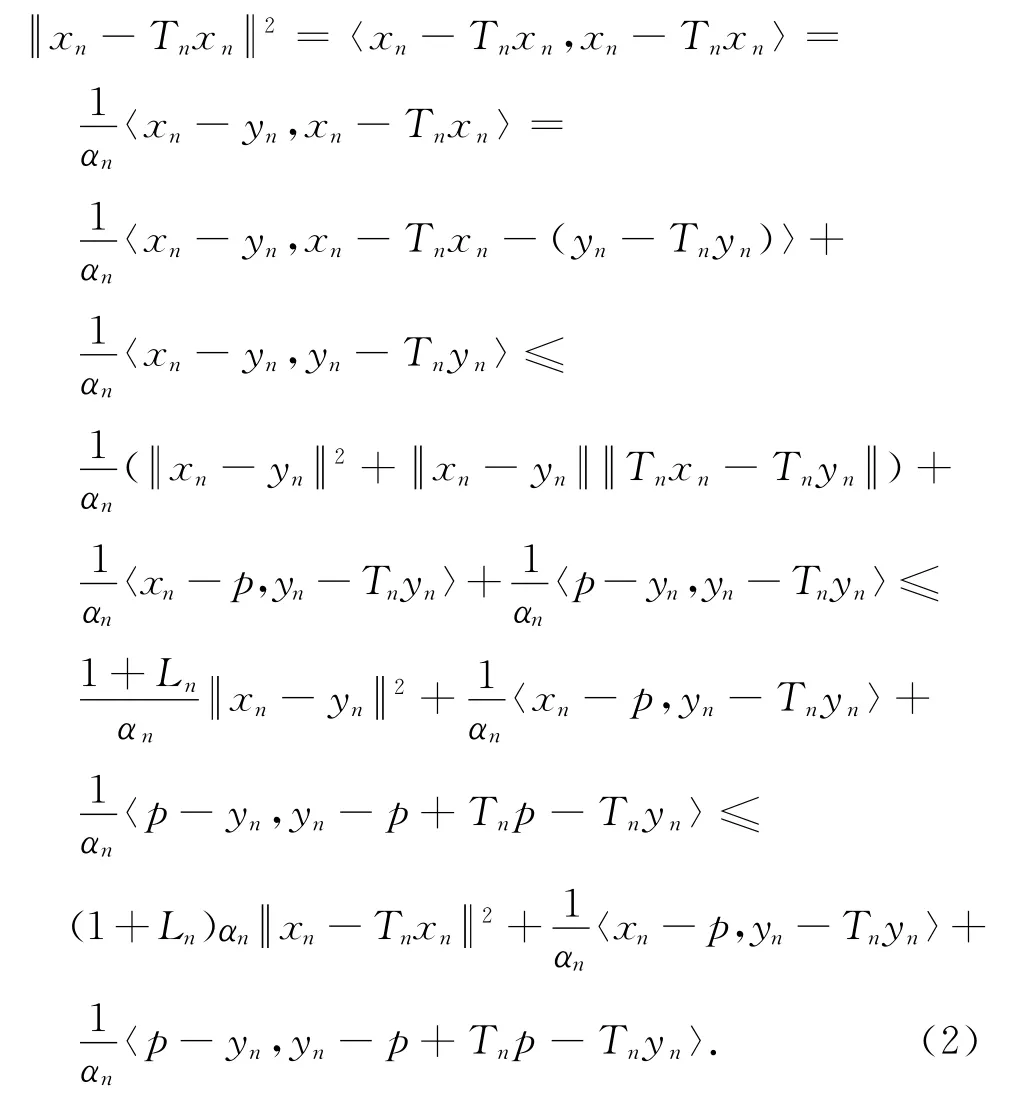
由于Tn是拟伪压缩映像，所以

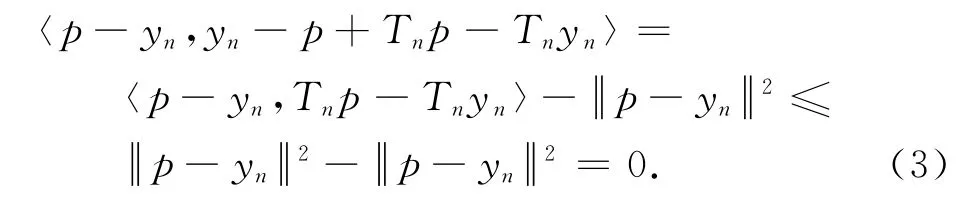
将式（3）代入式（2）可得

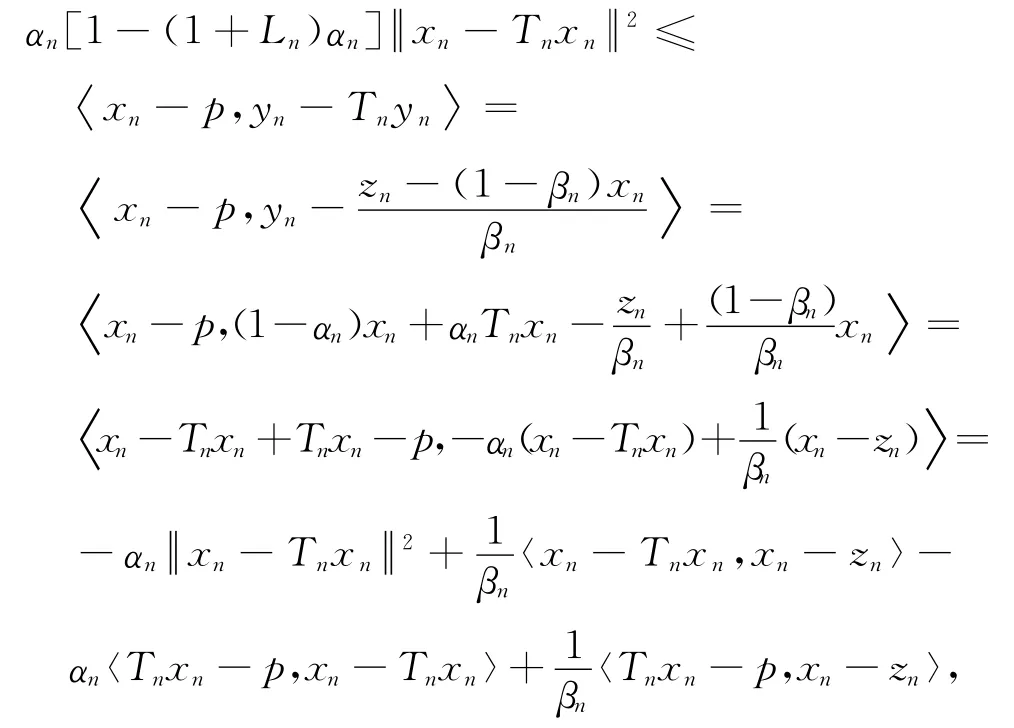
于是

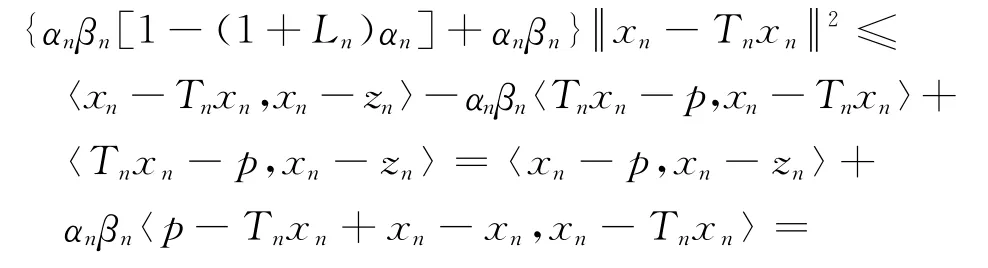
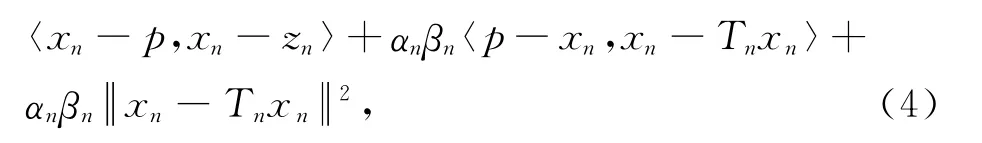
其中，

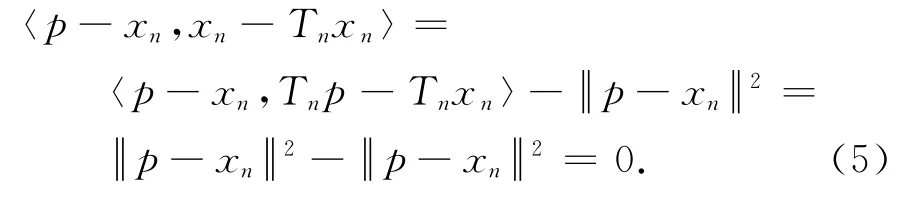
将式（5）代入式（4）可得

则p∈Cn＋1，于是F⊂Cn＋1．因此，对于任意n∈N，F⊂Cn，且｛xn｝有意义．

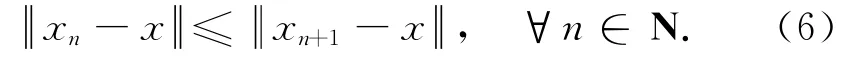
另一方面，由第2步可得F⊂Cn，从而

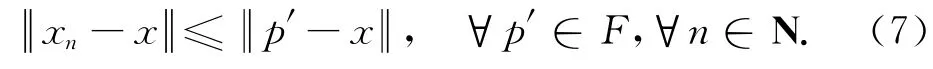
由引理2可得

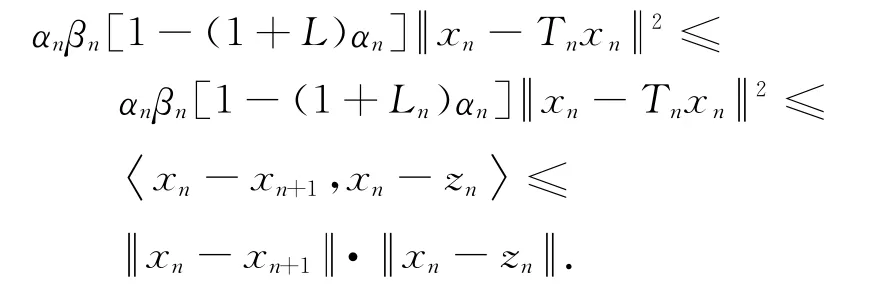
由｛αn｝，｛βn｝的假设和｛xn｝与｛zn｝的有界性可得

第6步 证明xn→PFx（n→∞）．

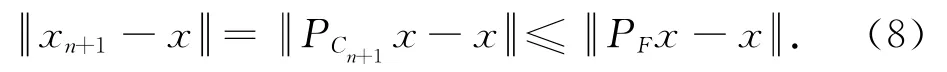
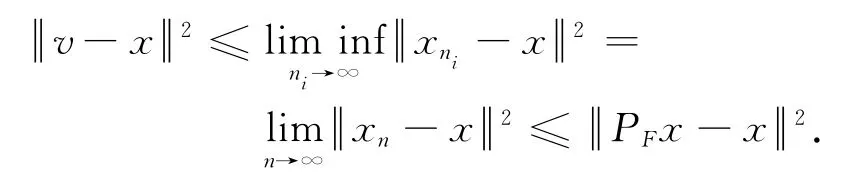
根据v∈F可得v＝PFx，所以，且

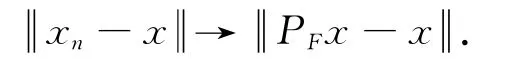
于是，

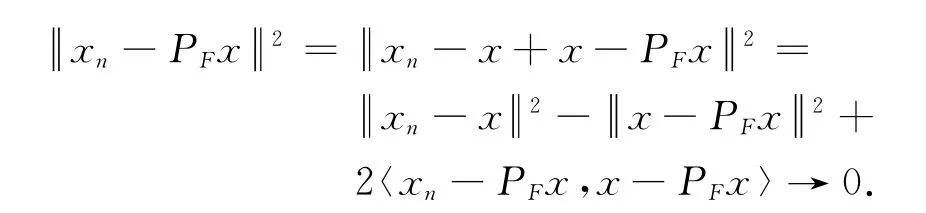
证毕．

注1 定理1将文献［3］定理3．2从固定非扩张映像族推广到Lipschitz拟伪压缩映像族，也将文献［3］定理3．4从非扩张映像族推广到Lipschitz拟伪压缩映像族，同时，定理1中的算法较文献［1］定理2．1中的算法简单．

定理2 设H是Hilbert空间，C是H的非空闭凸子集，｛Tn｝：C→H是kn－严格拟伪压缩映像族，使得．假设

（0，1），C1＝C，n∈N，x∈H，定义序列｛xn｝如下：

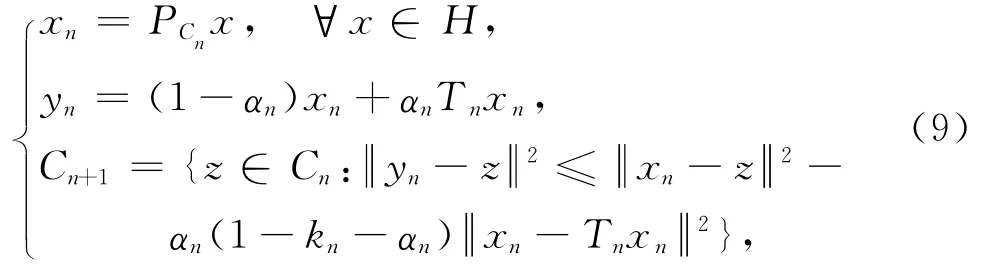
如果｛Tn｝满足条件（Z），那么｛xn｝强收敛于PFx．

证明 分6步完成证明．

第1步 根据引理4，类似于定理1第1步的证明，可得对于任意x∈H，PFx都有意义．

第2步 证明对于任意n∈N，Cn是C的非空闭凸子集．

显然，对于任意n∈N，Cn是C的闭凸子集．下面证明F⊂Cn，∀n∈N．

事实上F⊂C＝C1．假设对某一n∈N，F⊂Cn，对任意的p∈F，有p∈Cn．根据引理3和严格伪压缩映像的定义可得

则p∈Cn＋1．于是F⊂Cn＋1．因此F⊂Cn，∀n∈N．且｛xn｝有意义．

第4步 同定理1第4步的证明，可得

由于xn＋1∈Cn＋1，利用式（9）及引理3可得

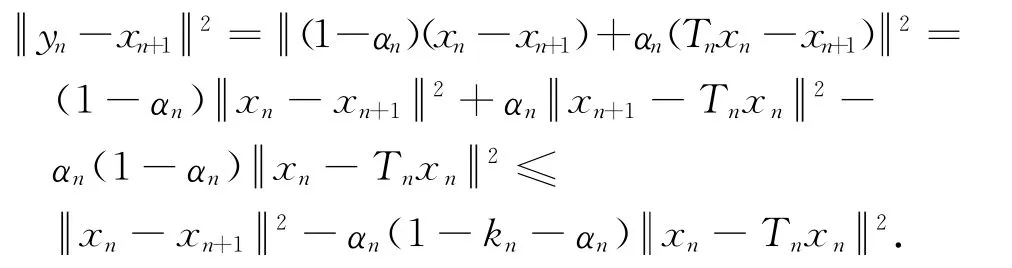
所以，

因为αn∈（0，1），所以

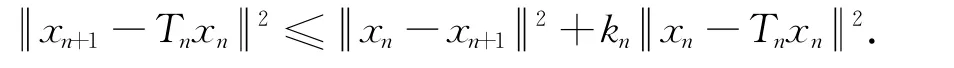
另外，

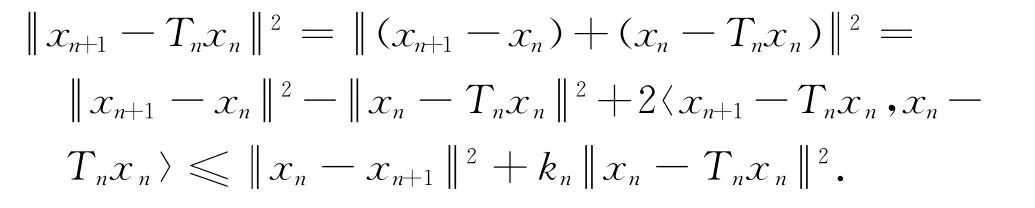
于是

从而

则

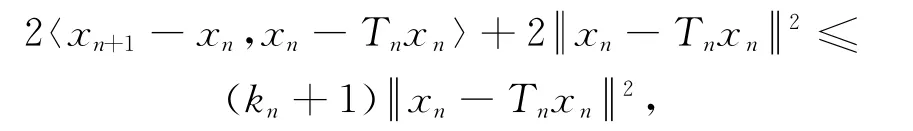
即

根据｛kn｝的假设及可得

第6步 同定理1第6步的证明，可得xn→PFx（n→∞）．

证毕．

注2 定理2将文献［3］定理3．2从固定非扩张映像族推广到严格拟伪压缩映像族，也将文献［3］定理3．4从非扩张映像族推广到严格拟伪压缩映像族，同时，定理2中的算法比文献［1］定理2．2中的算法简单．

参考文献（References）：

［1］ ZHOU H Y．Strong convergence theorems for a family of Lipschitz quasi－pseudo－contractions in Hilbert spaces［J］．Nonlinear Anal，2009，71：120－125．

［2］ ZHOU H Y．Convergence theorems of fixed points for Lipschitz pseudo－contractions in Hilbert spaces［J］．J Math Anal Appl，2008，343：546－556．

［3］ AOYAMA K，KOHSAKA F，TAKAHASHI W．Shrinking projection methods for firmly nonexpansive mappings［J］．Nonlinear Anal，2009，71：1626－1632．

［4］ MARINO G，XU H K．Weak and strong convergence theorems for strict pseudo－contractions in Hilbert spaces［J］．J Math Anal Appl，2007，329：336－346．

［5］ KIM T H，XU H K．Strong convergence of modified Mann iterations［J］．Nonlinear Anal，2005，61：51－60．

［6］ ZHOU H Y．Convergence theorems of fixed points forκ－strict pseudo－contractions in Hilbert spaces［J］．Nonlinear Anal，2008，69：456－462．

［7］ 王元恒，石惠敏．2个有限族广义依中心意义的渐近非扩张非自映像公共不动点定理［J］．浙江大学学报：理学版，2014，41（3）：282－287．WANG Yuanheng，SHI Huimin．Common fixed point theorems for two finite families of generalized asymptotically nonexpansive nonself－maps with the intermediate sense［J］．Journal of Zhejiang University：Science E－dition，2014，41（3）：282－287．

［8］ 高兴慧，马乐荣．Lipschitz拟伪压缩映像族的收缩投影算法［J］．数学的实践与认识，2014，44（20）：254－257．GAO Xinghui，MA Lerong．Shrinking projection methods for Lipschitz quasi－pseudo－contractions［J］．Mathematics in Practice and Theory，2014，44（20）：254－257．

［9］ ZHOU H Y，GAO X H．Iterative approximation of common fixed points for two quasnonexpansive mappings in Banach spaces［J］．Math Commun，2012，17：49－62．

［10］ GAO X H，ZHOU H Y．Strong convergence theorems of common elements for equilibrium problems and fixed point problems in Banach spaces［J］．Acta Mathematics Applicatae Sinica：English Series，2012，28 （2）：337－350．

［11］ 高兴慧，周海云，高改良．平衡问题和不动点问题的公共元的混杂算法［J］．数学物理学报：A辑，2011，31 （3）：720－728．GAO Xinghui，ZHOU Haiyun，GAO Gailiang．Hybrid algorithms of common elements for equilibrium problems and fixed point problems［J］．Acta Mathematics Scientia：Ser A，2011，31（3）：720－728．

［12］ GAO X H，ZHOU H Y．Shrinking projection methods for a family of quasstrict asymptotically pseudo－contractions in Banach space［J］．Journal of Mathematical Research and Exposition，2011，31（5）：905－914．

Strong convergence theorems for a family of Lipschitz quasi－pseudo－contractions

GAO Xinghui，YANG Chunping（College of Mathematics and Computer Science，Yanan University，Yanan 716000，Shaanxi Province，China）

Journal of Zhejiang University（Sci－ence Edition），2016，43（1）：071－074

Abstract：The purpose is to study the shrinking projection methods for a family of Lipschitz quasi－pseudo－contractions and a family of strict quasi－pseudo－contractions．Then，we proved two strong convergence theorems for their common fixed points by using the proposed projection algorithms in the framework of Hilbert spaces．The results presented in this paper improve and extend the corresponding ones announced by many others．

Key Words：shrinking projection method；a family of Lipschitz quasi－pseudo－contraction；common fixed points

作者简介：高兴慧（1975－），女，副教授，硕士，主要从事非线性泛函分析研究，E－mail：yadxgaoxinghui＠163．com．

基金项目：陕西省自然科学基础研究计划资助项目（2014JM2－1003）；陕西省教育厅科研计划项目（2013JK0575）；陕西省高水平大学建设专项资金资助项目（2012SXTS07）．

收稿日期：2015－03－04．

DOI：10．3785／j．issn．1008－9497．2016．01．012

中图分类号：O 177．91

文献标志码：A

文章编号：1008－9497（2016）01－071－04