太阳影子定位问题研究

吕长青,王兵，魏宗义，金燕琪，刘晓芳

(枣庄学院 a.数学与统计学院，b.信息与工程学院，山东枣庄　277160)



太阳影子定位问题研究

吕长青a,王兵a，魏宗义b，金燕琪b，刘晓芳b

(枣庄学院 a.数学与统计学院，b.信息与工程学院，山东枣庄277160)

[摘要]太阳影子定位是通过分析影子变化来确定视频拍摄的时间和地点，是视频分析研究的重要内容.论文通过太阳高度角公式建立直杆影子长度的数学模型；对于在已知不同时间的直杆影子的坐标情况下，通过非线性最小二乘拟合的方法确定直杆的坐标；对于只有直杆影子坐标情况下，通过函数拟合并运用遗传算法确定了直杆的坐标以及时间；作为应用计算了给定视频中直杆的位置.

[关键词]太阳高度角；非线性最小二乘法；遗传算法 ； MATLAB；视频处理

0引言

在现实生活中，可以通过影子长度就可以大致知道一天中的时刻，近代航海以及野外生存中，利用日晷可以确定所处方向与位置.在视频分析中，通过日影确定视频的拍摄地点和拍摄日期是视频数据分析的重要方面，太阳影子定位技术就是通过分析视频中物体的太阳影子变化，确定视频拍摄的地点和日期的一种方法.

文[1]中根据日影在已知时间情况下，确定物体所在位置以及方向，但都需要依据当地时间来计算，对于当地时间不知情况下，无法确定物体的位置.论文通过建立直杆影子的数学模型，根据影子长度变化的数据，利用数据拟合的方法确定物体的位置克服了利用当地时间的弊端.在刑事侦查、反恐通过视频分析确定嫌疑人的位置有着重要的应用.

注：论文所采用数据来自于2015全国大学生数学建模竞赛A题.

1模型假设与符号说明

1.1模型假设

为了简化计算假定(1)大气和云层的对太阳光没有影响；(2)地球自转的没有影响；(3)假设太阳为唯一光源；(4)假设太阳光是平行光；(5)假设地球为光滑规则的球体；(6)假设附件4中的视频时间为北京时间.

1.2符号说明

l：杆长；l′：影长；θ：太阳高度角；h：地方恒星时系统下的时角；

δ：太阳赤纬Φ ：当地纬度；th：小时；tm：分钟；

ts：秒Ta：北京太阳时；Tb：当地太阳时；Wt：经度差；

t：北京时间tL：当地时间；N：该日在一年中的第N天

2直杆影子长度数学模型

2.1问题分析

影长l′长度主要与杆长l和太阳高度角θ有关，即l′=f(l,θ)；对于θ与时角 h、赤纬δ、纬度Φ有关，根据太阳高度角公式sin(θ)=cos(h)cos(δ)cos(Φ)+sin(δ)sin(Φ)[2](*)可以确定.

由文献[3]可知，时角h为天体赤经与当地恒星的差值，每相差一小时，经度相差15°；时角计算时，应计算直杆所处位置(东经116°23′29″)，而非北京时间(东经120°)，可以减小误差.赤纬为天体坐标数据之一，是纬度在天体上的投影，太阳赤纬的最高度数为23°26′.

2.2模型建立

太阳高度角是太阳光线与当地地平线所交的最小线面角(如图1所示)，

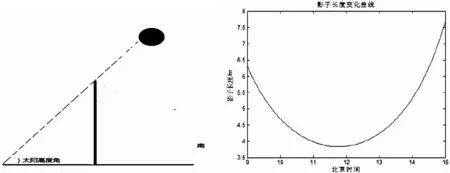
图1　太阳高度角　　　　　　　　　　图2　影子长度变化曲线

由图1可知直杆、影子与太阳光线之间形成直角三角形，则有

l′=lcot(θ)

(1)

对于太阳高度角θ，则由公式(2)确定

sin(θ)=cos(h)cos(δ)cos(Φ)+sin(δ)sin(Φ)

(2)

其中时角 h、赤纬δ可由公式(3)

(3)

由公式(1)～(3)可得影长 l′.通过此模型求解具有一定误差，因此利用当地太阳时Td[4]的计算，

Td=Tb-4Wi

(4)

可以适当减小误差，减小纬度不匹配对所带来的误差.

2.2模型求解

对于条件

(5)

代入(1)～(3)进行，利用MATLAB得出影子长度变化曲线，如图2所示.

2.4结果分析

由影子长度变化曲线(图2)可知，在同一地点的影子长度随着太阳高度角的增大而减小，也随着时间的变化先减小后增大，在正午时分影子长度达到最小，太阳高度角达到最大.

3已知时间的地点模型

3.1模型分析

1)由图2可知，太阳影子长度与时间近似为抛物线，可以假定太阳影子长度与时间成二次函数.将附件1中的数据绘制散点图(见图3)，可近似为二次曲线，利用该数据对方程(1)～(3)的参数进行非线性最小二乘拟合，可以得到该地点直杆的影长与时间的经验方程.

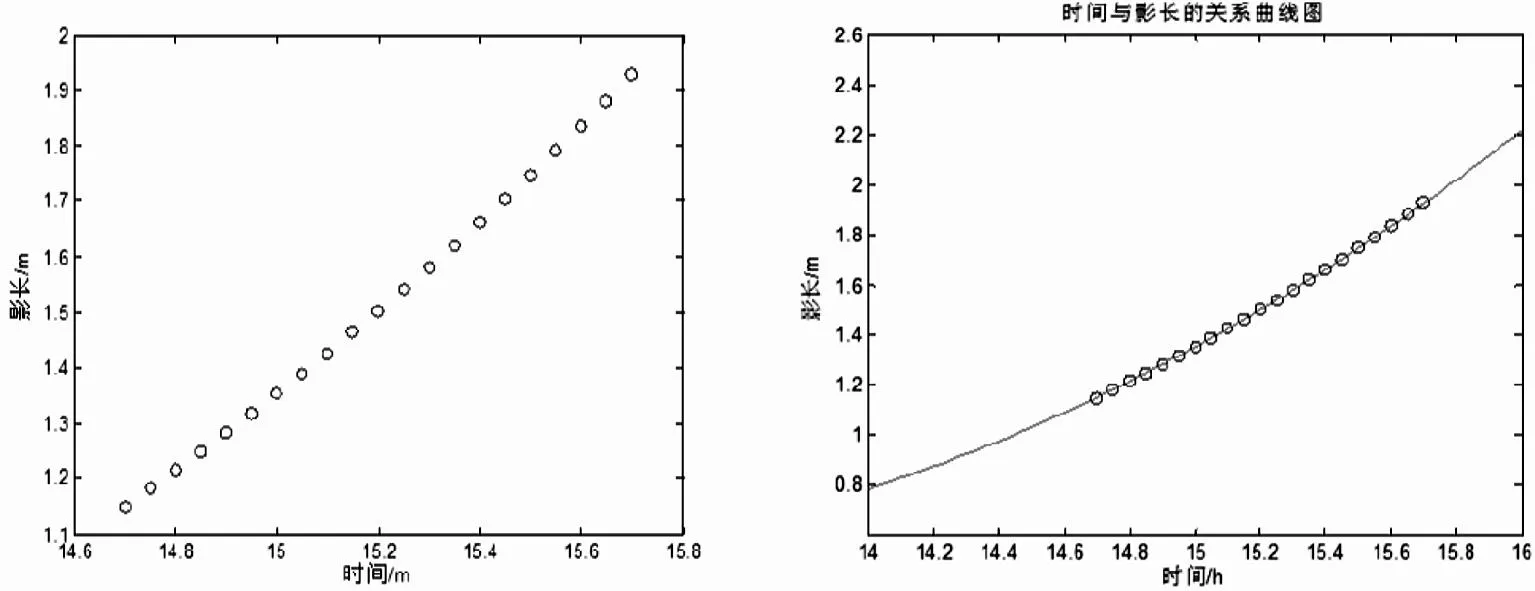
图3　影子长度散点图　　　　　　　图4 时间与影长的关系曲线图

3.2模型的建立

l′=at2+bt+c

(6)

利用不同时刻直杆影子顶点坐标，进行非线性拟合，可得参数a,b,c值，a=0.1489，b=-3.7519，c=24.1275.由此可得方程

l′=0.1489t2-3.7519t+24.1275

(7)

Td=Tb-4Wl

(8)

可得此地经度为东经105°1′58.8″.

3.3模型的求解

由于

(9)

并且由l′=lcot(θ) 与θ=asin(cos(h)cos(δ)cos(Φ)+sin(δ)sin(Φ)) 可得

(10)

方程中时间为自变量，杆长l、经度E、纬度Φ为未知参数，利用附件1中的时间以及所求影长的数据中对参数进行拟合，得到拟合参数

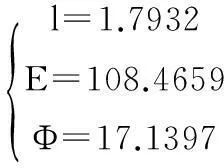
(11)

即可得到直杆位置坐标：东经108°27′57.24″北纬17°8′22.92″，根据中国经纬图推算，地点位于中国海南省西南附近.

3.4结果分析

利用对时间长度进行函数拟合处理，得到经度的大致位置为：东经105°1′58.8″，然后对参数进行非线性最小二乘法参数估计，得到相对准确的经度东经108°27′57.24″和纬度北纬17°8′22.92″通过两种方法结合得出比较可能的地点，即中国海南省.

4未知时间的地点模型

4.1模型分析

对于未知时间的直杆影长数据，如果直接采用参数拟合的方法，将得到许多近似解，在实际中无法使用，这里利用遗传算法的全局搜索能力对网格中的经纬度筛选，以影长和实际影长的比例作为适应度，建立基于遗传算法的太阳影子定位模型，模型建立流程图.

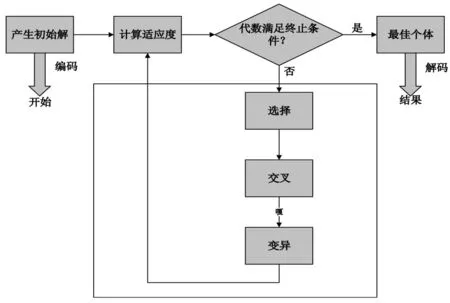
图5　遗传算法的流程图

遗传算法步骤：

(1)评估计算每个影长的适应度；

(2)通过随机数产生新的经纬度坐标；

(3)对经纬度进行投影长度进行计算；

(4)比较新产生经纬度舒适度与远经纬度的法查大小；

(5)重复进行(2)(3)(4)指导计算出最优解.

将遗传算法的最优解进行非线性最小二乘拟合，得出最优解.

4.2模型建立

建立遗传算法(此处采用附件2数据，利用C++编码)

(1)编码：把已知的影长进行编号：

doubleD0[21]={1.247256205,1.22279459…………0.850504468};

(2)利用随机数函数，产生经纬度：aa1=(-90+180*rand()/(RAND_MAX));

(3)根据时间得出太阳高度角：

Fi_a=asin(sin(AngleToPi(23,26,0))*sin(AngleToPi(2*Pi*(T+10)/365,0,0)));

(4)求出在该时间下的投影长度：

peta=Pi/2-acos((xa*xc+ya*yc+za*zc)/(sqrt(xa*xa+ya*ya+za*za)*sqrt(xc*xc+yc*yc+zc*zc)));D=l0/tan(peta);lc[i/3]=D;

(5)交换，对于新的影长进行匹配交换：

s1+=(((lc[i2]/D0[i2])-average)*((lc[i2]/D0[i2])-average));

(6)适应度估计：采用方差对遗传算法进行适应度估计：

(12)

(13)

n表示可能的拍摄地点，则该影长的适应度记为：

(14)

即适应度为影长与原始影长相似度，优化的目标就是选择适应度函数尽可能大的影长，适应度函数值越大的影长越优质，反之越劣质.

通过遗传算法计算，得出经纬度的可能解，见下表：

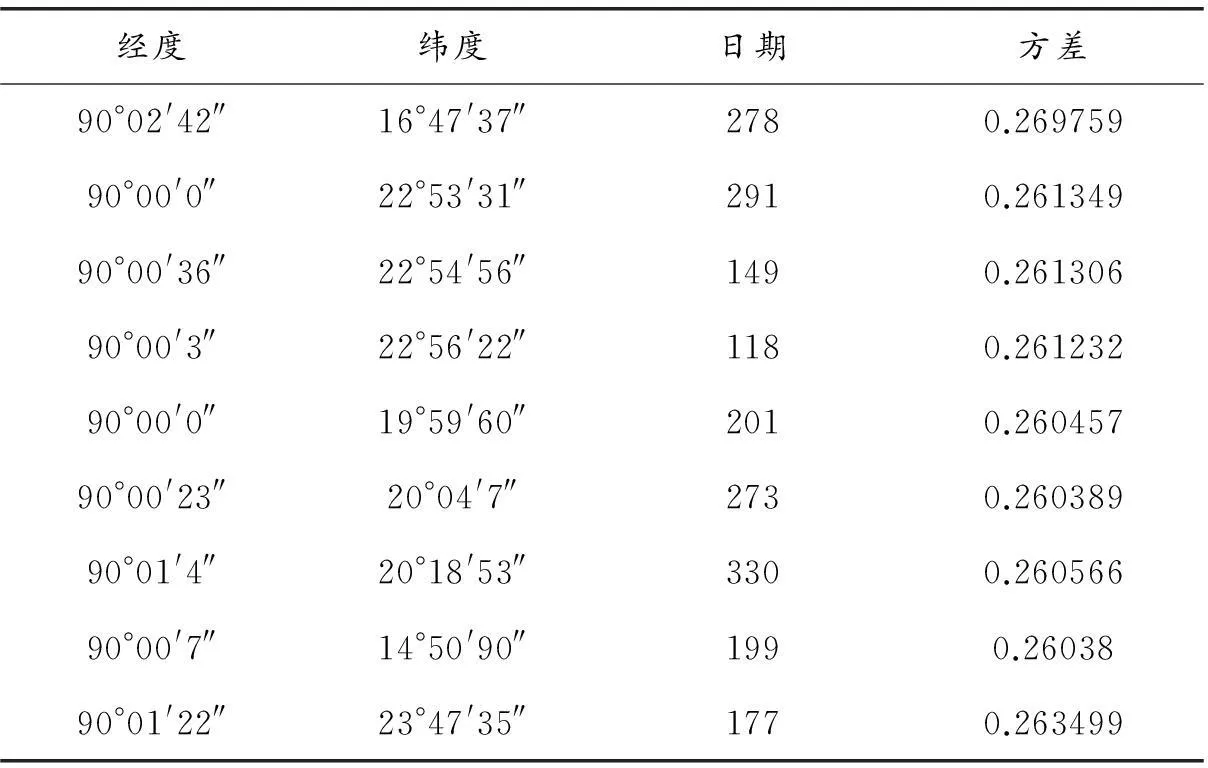
表1　遗传算法得出可能的经纬度

4.3模型求解

对于表1中的经纬度、日期通过非线性最小二乘拟合对公式

以已知经度纬度日期值近似值作为初值进行拟合，得出经度为90°00′53″，纬度为20°18′35″，时间为7月19日，位于新疆自治区.

同理，对附件3中的数据进行计算，得出经度为112°14′21″，纬度为27°38′24″，时间为2月11日，位于湖南省.

5模型的应用

对于给定的视频，利用MATLAB软件，对视频进行数据提取.首先确定视频的帧数总数，将视频按照相同的时间间隔分为47份，用MATLAB读取视频，从间隔相等的视频中提取此47张图片，将提取的彩色图片进行灰度处理，对得到的灰度图片进行二值化分析；从该视频中提取出视频录制的时间(T)、直杆的实际长度(l)以及直杆影子(l′)随时间不断变化的长度，从而可以得到该段视频中包含的所需要数据信息.

通过下面模型

(15)

利用采集视频数据，用matab进行拟合，可得视频拍摄位置经度为111°22′43″，纬度为41°05′05″，位于呼和浩特市附近.

参考文献

[1]张明涛.利用太阳定位的几种方法[DB/OL]. http://wenku.baidu.com/link?url=f-3yl_hYZh7bqeS_A8WhGavg4x3c4yrrd9TfkZKXqLuQNcuQ_2ag12iQMnr3EYU7ITAsiUDpD2WhC3iUdGiEh5BzORkWMtkY4wcjSpjdNda,2012-12-17/2016-1-9.

[2]维基百科.太阳高度角[DB/OL].https://zh.wikipedia.org/wiki/%E5%A4%AA%E9%98%B3%E9%AB%98%E5%BA%A6%E8%A7%92,2015-9-11.

[2]李玉海.太阳高度角及其计算[J].气象,1977(4):27-28.

[3]邱国全.太阳时的计算[J] .太阳能,1998(1):7-7.

[4]陈小平.遗传算法在函数优化中的应用研究[D].苏州:苏州大学，2008.

[5]余成波.数字图像处理及MATLAB实现[M].重庆:重庆大学出版社，2003.

[6]赵静,但琦.数学建模与数学实验[M].北京:高等教育出版社，2010.

[责任编辑：房永磊]

Research on Location of Straight Pole Through Sundial

LV Chang-Qinga，WANG Binga，WEI Zong-yib，JIN Yang-qib，LIU Xiao-fangb

(a. School of Mathematics and Statistics; b.School of Information Science and Engineering,Zaozhuang University, Zaozhuang 277160,China)

Abstract：Using formular of solar attitude, the mathematical model of length of straight pole was set up. When the time of photograph given, the coordinate of the straight pole was located by nonlinear least squares fitting method.When the time of photograph not given, the coordinate of the straight pole and time of photograph were determined through genetic algorithm and nonlinear least squares fitting method . As application ,the location of straight pole in a video was determined by video processing.

Key words：solar attitude; nonlinear least squares fitting method ; genetic algorithm; matlab; video processing

[中图分类号]O29

[文献标识码]A

[文章编号]1004-7077(2016)02-0035-06

[作者简介]吕长青(1973-)，男，山东滕州人，枣庄学院数学与统计学院副教授，理学硕士，主要从事应用数学理论与应用研究.

[基金项目]国家级大学生创新创业训练计划项目(项目编号：201510904050)；枣庄学院教学研究项目(项目编号：YJG13007).

[收稿日期]2016-01-20