Wake Numerical Simulation of Wind Field Based on Two Modified Wind Engineering Models

Yang Xiangsheng，Zhao Ning，Tian LinlinJiangsu Key Laboratory of Hi-Tech Research for Wind Turbine Design，Nanjing University of Aeronautics＆Astronautics，Nanjing 210016，P.R.China(Received 18 August 2015; revised 2 December 2015; accepted 5 January 2016)



Wake Numerical Simulation of Wind Field Based on Two Modified Wind Engineering Models

Yang Xiangsheng，Zhao Ning*，Tian Linlin
Jiangsu Key Laboratory of Hi-Tech Research for Wind Turbine Design，Nanjing University of Aeronautics＆Astronautics，Nanjing 210016，P.R.China
(Received 18 August 2015; revised 2 December 2015; accepted 5 January 2016)

Abstract:With the assumption of the Park model that the wake region is in linear expansion and the cross-wind is in multinomial and Gaussian distribution in wake region，one develops the Park-polynomial model and the Park-Gaussian model to numerically simulate the wake flow field for a single wind turbine.Compared with the measured data of wind farm and the wind tunnel test，it shows that the prediction precision of wake field has been improved obviously under the modified initial wake radius.Moreover，both of the newly modified two models could well simulate the wind velocity in wake region，because the predicted results is approximately consistent with the test result，and the cross-wind distribution conforms to that of the real flow field.The two models have still inherited many advantages of engineering models，such as simple form，easy-to-code，and high computational efficiency.Particularly，the Park-Gaussian model is the best in overall performance among them.

Key words:Park-polynomial model; Park-Gaussian model; wind turbine; wake

CLC number: TK89; TM614Document code: AArticle ID: 1005-1120(2016)01-0053-07

* Corresponding author，E-mail address: zhaoam@ nuaa.edu.cn.

How to cite this article: Yang Xiangsheng，Zhao Ning，Tian Linlin.Wake numerical simulation of wind field based on two modified wind engineering models［J］.Trans.Nanjing Univ.Aero.Astro.，2016，33(1) : 53-59.

http: / /dx.doi.org/10.16356/j.1005-1120.2016.01.053

0　Introduction

Wind turbine layout optimization is an important part in the early stage of wind farm construction，in which wake effect is one of the main factors to be considered in determine the micrositting of wind turbines.The wake effect is primarily investigated via three ways: wind farm measurement，wind tunnel test and numerical simulation.

Wind farm measurement includes the measurement of a single wind turbine and of a group of wind turbines.Sexbierum wind farm［1］，Tjæreborg wind farm［2］and Nibe wind farm［3］are built largely for the investigation of the single wind turbine，while Nysted wind farm［4］，Horns Rev wind farm［5］and other wind farms are mostly for the group measurement.Although wind farm measurement has the advantage of being true and reliable，in the wind farm measurement the full-scale and high-quality test required is time- and money-consuming.What is more，global optimization of the wind turbines layout is unable to be completed through the test.

As for the wind tunnel test，it is a process that simulates all kinds of running states of the wind turbine model to obtain the test data of wake flow.Alfredsson et al.［6］discharged cut-in flow from the blade tip with smoke and qualitatively studied the wake effect of a single wind turbine by the visualization method.Besides，Hand et al.［7］made a detailed analysis on wake structures in near wake region through wind tunnel tests.In addition，DNW［8］in Energy Research Center of the Netherlands measured the data in near wake region using the particle image velocimetry (PIV) technology.The wind tunnel test has many advantages of highly precise results，poor sensitivity to weather and time，easy availability of the single wind regime effect on wake flow.However，it has its own limits.For exam-ple，it is vulnerable to the interference of boundary effect，and it is susceptible to the factor that similarity criterion is unable to be satisified (the most common is the Reynolds number) and other factors.

Wake numerical simulation model can be divided into three categories，i.e.，the empirical model，the vortex theory model and the CFD model basedonsolving Navier-Stokes (N-S ) equations［9］.In 1980s，Jensen［10］(1983 ) and Katic et al.［11］(1986) proposed the Park model.As an empirical model，it assumes that the wind velocity loss in wake region is related to a wake attenuation constant k，and the wind velocity in the cross-wind direction is in constant distribution.The simple form of the Park model has a high computational efficiency.It was reported that in this Park model，wind velocity loss in wake region is underestimated，and the velocity distribution in the cross-wind direction is not in conformity with the real flow field.To solve the problem，Tian［12］proposed a 2D Jensen model，using the cosine curve to describe the wind velocity distribution in the cross-wind direction.

Based on the observation of other researchers［13］，it is found that in real flow field，the shape of the wake velocity in the cross-wind direction can be fitted by the multinomial curve or Gaussian curve.With the purpose of accurately estimating the wake flow，the multinomial and Gaussian curves are employed to simulate the distribution of the wake velocity in the normal-wind direction.Here，we produce two new modified engineering wake models，named as the Park-Polynomial model and the Park-Gaussian model.In order to test the performance of these two new modified wake models，a number of numerical simulations are carried out on various types of wind turbine which work under different wind conditions.

1　Engineering Wake Models

1.1Park model

The Park wake model proposed by Jensen［10］has been widely-used to the wind resource analysis software WAsP and other commercial softwares.The model is based on the principle of momentum conservation.

where r0is the initial wake radius in the rotor，v0the wind velocity at the initial wake radius，rxthe wake radius from the disk x，u*the wind velocity at the wake radius from the disk x，and u0the incoming wind velocity.Wherein，rx= kx + r0and k is the rate of expansion in wake region.

When the surface roughness of the land where the wind turbine installed is unknown，generally we can set the k value of 0.075 for the onshore wind turbine and 0.05 for the offshore wind turbine at the suggestions of Barthelmie et al.［13］.If the surface roughness is able to be measured，the empirical formula proposed by Frandsen et al.［14］could be adopted

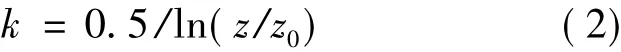
where z is the hub height and z0the surface roughness.

In the Park wake model，it is assumed that the wake region is in a fully turbulent flow state，and tip vortex and other phenomenons can be ignored.This leads to the fact that the Park wake model is unable to accurately simulate characteristics in the near wake region.

According to the actuator disk theory，it can be deduced that

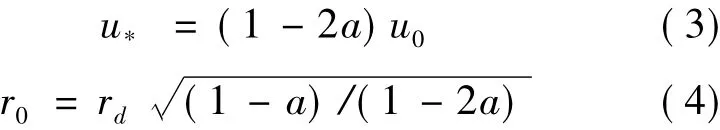
where a is the axial induced factor，and rdthe rotor radius.Substituting Eqs.(3) and (4) into Eq.(1) leads to

1.22D Jensen model

The Park wake model assumes that the wake velocity only varies from the down-stream distance x in the along-wind direction，and the wind velocity is constant in the cross-wind direction.Taking into account the free stream flow in the outside of the wake region，it can be found that the crosswind velocity is in a hat-shaped distribution，so the Park wake model is also known as the top-hatmodel.Nevertheless，thanks to the investigations of other researchers［13］and the experiments，it was oberserved that the top-hat distribution is inconformity with the true wake field.To overcome this problem，Tian［12］proposed the modification of the 2D Jensen model，using a cosine curve to describe wind velocity distribution in the crosswind direction.

The 2D Jensen wake model mainly has two steps.

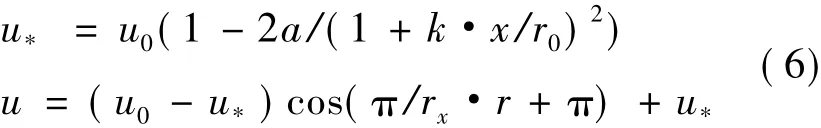
Compared with the Park model，the 2D Jensen model has improved the cross-wind trend.Here we propose two modification models，whose crosswind trends are consistent with the trend in real flow field.

1.3Modification of the Park-polynomial model From the test measurement［13］it is known that，the wake wind velocity in real flow field is in multinomial distribution or Gaussian distribution in the cross-wind direction.As a result，combined with the assumption of the Park model that the wake region is in linear expansion and the crosswind velocity is in quadratic polynomial distribution in the wake region，we propose a new modified Park-polynomial model.The sketch of the proposed wake model is shown in Fig.1.

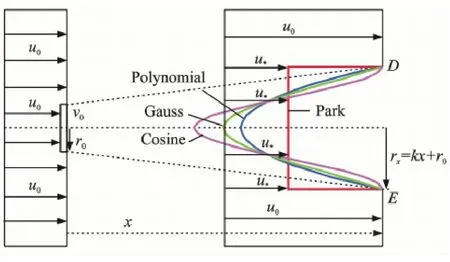
Fig.1　Sketch of the proposed wake model

Assuming that the Park-polynomial model has the following form

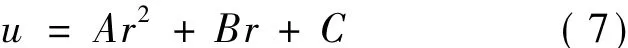
where A，B and C are the undetermined coefficients，and r the distance to rotor center in the cross-wind direction.Since the model is an improvement based on the Park model，the following assumptions are satisfied:

(1) When the cross-wind distance r expands to the wake radius rx，the wind velocity at D and E recovers to the incoming wind velocity u0.

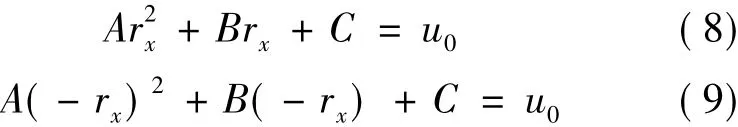
(2) The wake radius as well as mass flux (i.e.area covered by the velocity is identical) of both models are the same.

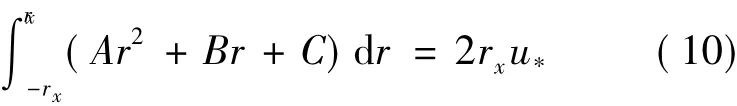
where u*is the calculated value with the original Park wake model at rx.

Considering Eqs.(8)—(10)，we have

Then substituting Eq.(11) into Eq.(7)，the equation becomes

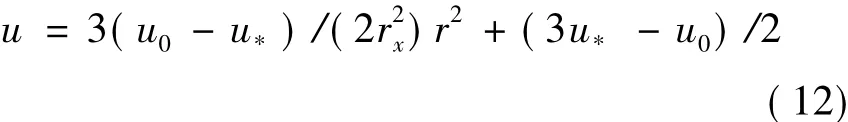
To sum up，it can be concluded that the Parkpolynomial model mainly has two steps:

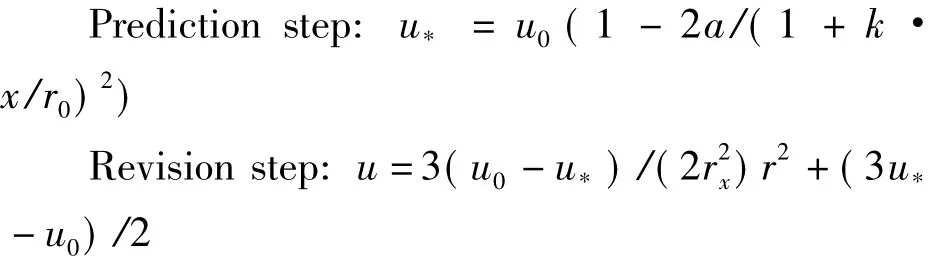
1.4Modification of the Park-Gaussian model

In combination with the Park model and the eddy-viscosity model，we put forward another new modified wake model，the Park-Gaussian model.It assumes that the wake region is in linear expansion with an expansion rate of k，and the wind velocity in the cross-wind direction is in Gaussian and symmetrical distributions，making it more likely be close to the real wake field.Sketch of the Park-Gaussian model is shown in Fig.1.

Assume that the Park-Gaussian model is

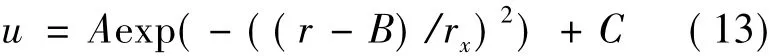
where rxis the wake radius at x in the downstream of the wind turbine，and r the distance to rotor center in the cross-wind direction.Since the Park-Gaussian model is proposed based on the Park model and the eddy-viscosity model，the following assumptions aremet:

(1) When the cross-wind distance r expands to the wake radius rx，the wind velocity at D and E recovers to the incoming wind velocity u0.

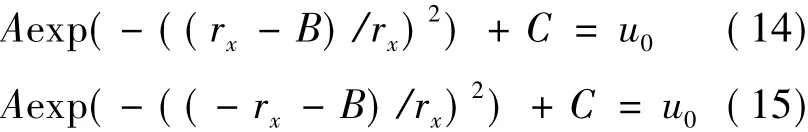
(2) The wake radius as well as mass flux (i.e.area covered by the velocity is identical) of both models are the same.

Substituing B = 0 into Eq.(16)，Eq.(18) is obtained.

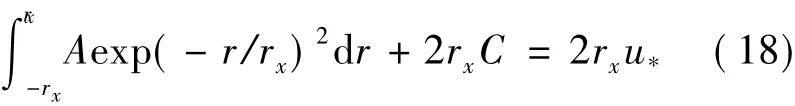
Since exp(－r/rx)2does not have a primitive function，here the approximate value of power series expansion is used for calculation.

Consider Eqs.(17) and (21)，A，B and C could be solved.

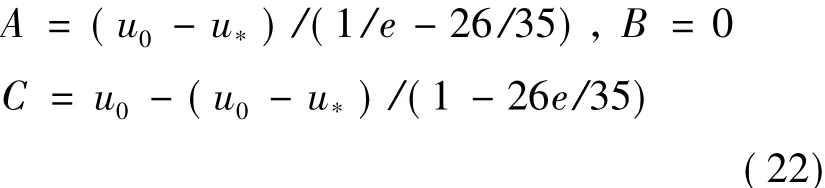
Then substitute Eq.(22) into Eq.(13)，and lead to

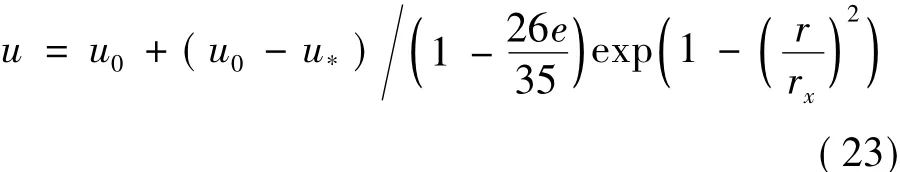
To sum up，it can be concluded that the Park-Gaussian model mainly has two steps:

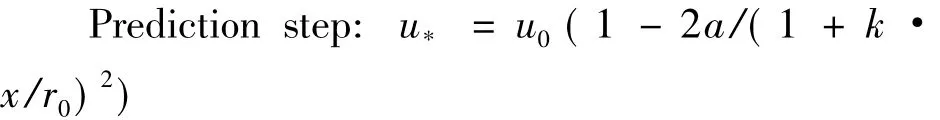
Revision step:

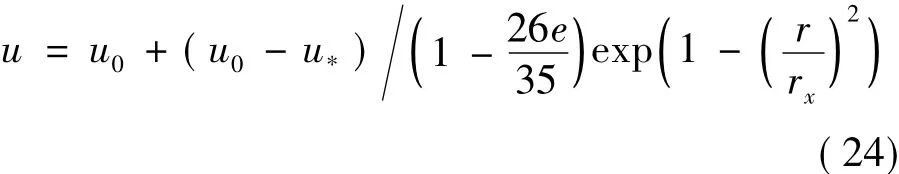
2　Results and Comparison with Experiments

2.1Measured data of Sexbierum wind farm

Sexbierum［1，12］measured wind fields have been arranged with 18 wind turbines with the following parameters: the rated power being 310 kW; the rotor diameter D =30.1 m (round to 30 m) ; the hub height z =35 m; the cut in speed uin=5 m/s; the rated speed u =14 m/ s; the cut off speed uout=20 m/s.Seven meteorological masts have been installed around the wind field，and used to measure the wind velocity，wind direction，air pressure，temperature，etc.In addition，wake data has been measured particularly at 2.5D，5.5D and 8.0D positions in the downstream of one of the wind turbines.The incoming wind velocity is u0=8.5 m/s，the wind turbine thrust coefficient CT=0.75，and the incoming turbulence intensity I0=10%.

F-M2.5D-S represents the cross-wind wake measured data at 2.5D in the downstream of the wind turbine in the Sexbierum wind field; P-U-2.5D-r0represents the cross-wind wake wind velocity of the Park model at 2.5D in the downstream of the wind turbine when r0= rd·P-G2.5D-r0represents the cross-wind wake wind velocity of the Park-Gaussian model at 2.5D in the downstream of the wind turbine when r0; P-P2.5D-r0represents the cross-wind wake wind velocity of the Park-polynomial model at 2.5D in the downstream of the wind turbine when r0; P-C2.5D-r0represents the cross-wind wake wind velocity of the 2D Jensen model at 2.5D in the downstream of the wind turbine when r0，and so on.RSM［15］represents that the method based on actuator disk concept is used to simulate wind turbine，and Reynolds stress turbulence model is adopted.

Figs.2—4 show that for the Park model，the underestimation of wake effect has been improved significantly withthe modifiedwake radius r0= rdAt 2.5D，5.5D and 8.0D in the downstream of the wind turbine，the wind velocity is 38.3%，17.2% and 12.3% higher than thetest data，respectively.As for the RSM model，at the 2.5D position the velocity is greater than the measured data，at the 5.5D and 8.0D downstream the velocities are close to the test data.The cross-wind velocity show a trend far away from the measured data.When referring to the 2D Jensen model，the wind velocity is slightly greater than the measured data with the modified wake radius r0=rd·， and compared to the RSM model，the cross-wind trend has been improved.For the Park-polynomial model，the cross-wind velocity of the Park-polynomial model approaches to the test data with the modified wake radius r0=rdAt 2.5D，5. 5D and 8.0D in the downstream of the wind turbine，the cross-wind velocity is 11.1%，4.3% and 4.8% higher than the test data，respectively.Concerning Park-Gaussian model，the cross-wind velocity of the Park-Gaussian model is closer to the test data with the modified wake radius r0= rd·. At 2.5D，5.5D and 8.0D in the downstream of the wind turbine，the cross-wind velocity is almost consistent with the test data.

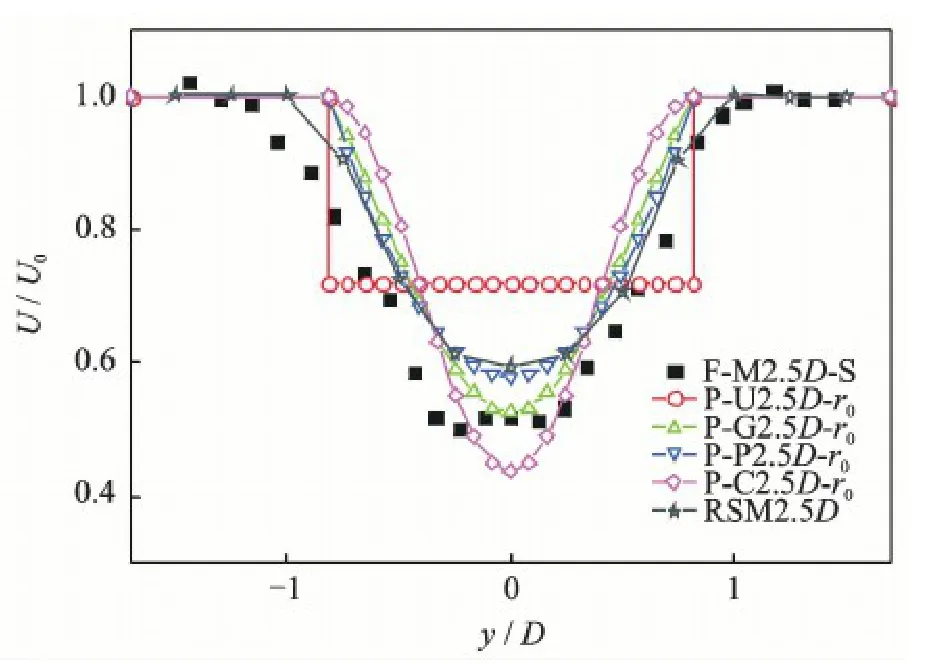
Fig.2　Cross-wind velocity distributions at 2.5D in the downstream of the Sexbierum wind turbine

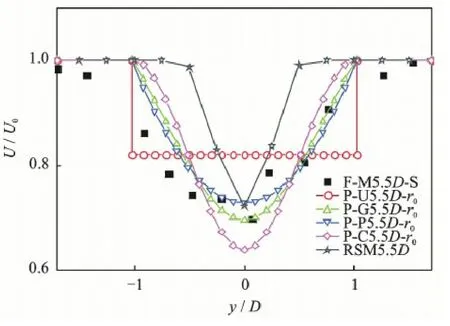
Fig.3　Cross-wind velocity distributions at 5.5D in the downstream of the Sexbierum wind turbine

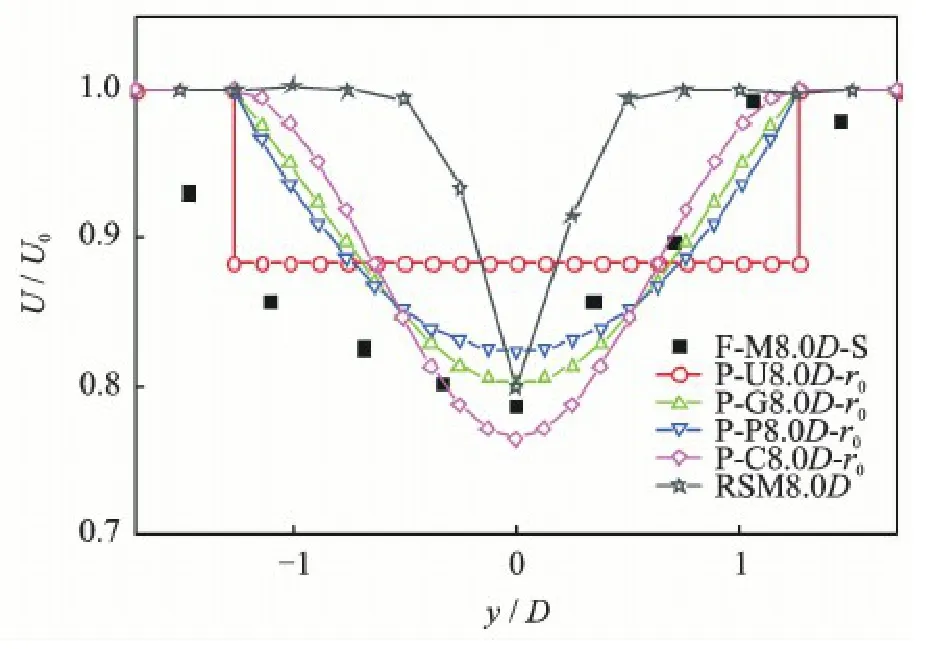
Fig.4　Cross-wind velocity distributions at 8.0D in the downstream of the Sexbierum wind turbine

2.2Experimental data of Garrad Hassan wind tunnel

In 1989，Garrad Hassan［16］the world's largest wind-energy consulting company has conducted a series of wind tunnel experiments for wind turbine wake.Objects selected for the test are horizontal axis wind turbine models with a rotor diameter of 0.27 m.The compression ratio is 1∶160.The corresponding simulative wind turbine is with a rotor diameter of D =43.2 m and a hub height of z =50 m.The service environment is on a flat terrain whose surface roughness is 0.075 m and area is 2 km×2 km.The incoming wind velocity is u0=5.3 m/s，the tip speed ratio λ1=2.9 and the thrust coefficient CT=0.62.

The analysis of Figs.5—7 shows that for the Park model，the underestimation of wake effect has been improved significantly with the modified wake radius r0= rd.At 5.0D，7.5D and 10D in the downstream of the wind turbine，the cross-wind velocity is 17.5%，8.1% and 0.6% higher than the test data，respectively.With regard to the 2D Jensen model，the wind velocity is lower than the measured data with the modified wake radius r0= rd，and the cross-wind trend has been improved.As for the Park-Polynomial model，the trend of its cross-wind velocity is close to the test data with the modified wake radius r0= rd.Significantly，at 5.0D，7.5Dand 10D in the downstream of the wind turbine，the cross-wind velocity is very close to the test data.As for the Park-Gaussian model，the trend of its crosswind velocity also agrees well with the test data with the modified wake radius r0= rd. At 5.0D and 7.5D in the downstream of the wind turbine，the cross-wind velocity almost coincides with the test data，except for the case at 10D，in which the cross-wind velocity is slightly lower than the test data.

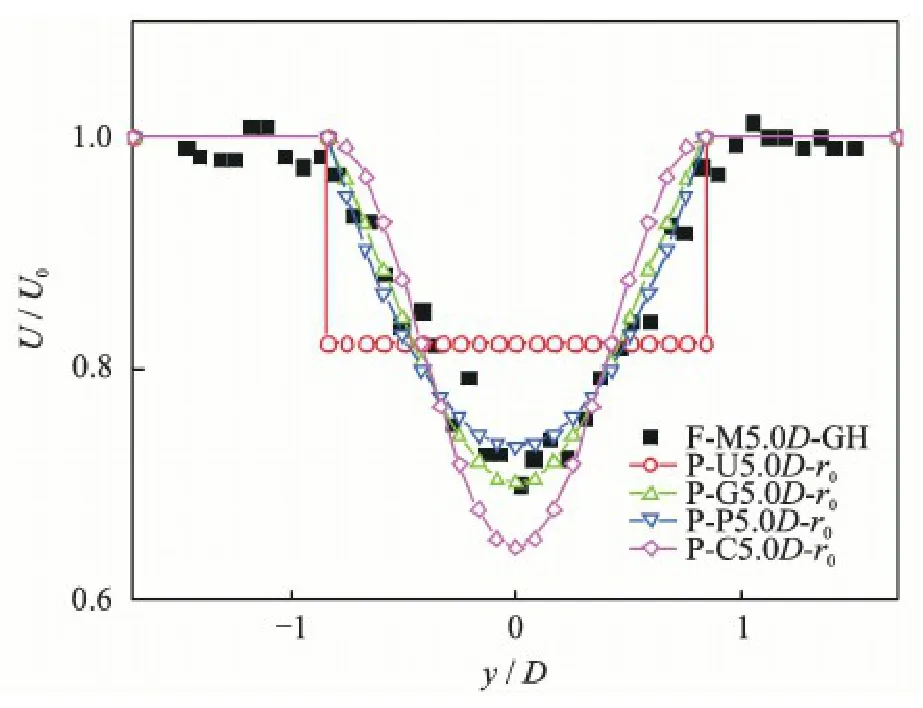
Fig.5　Cross-wind velocity distributions at 5.0D in the downstream of the Garrad Hassan wind turbine

Fig.6　Cross-wind velocity distributions at 7.5D in the downstream of the Garrad Hassan wind turbine

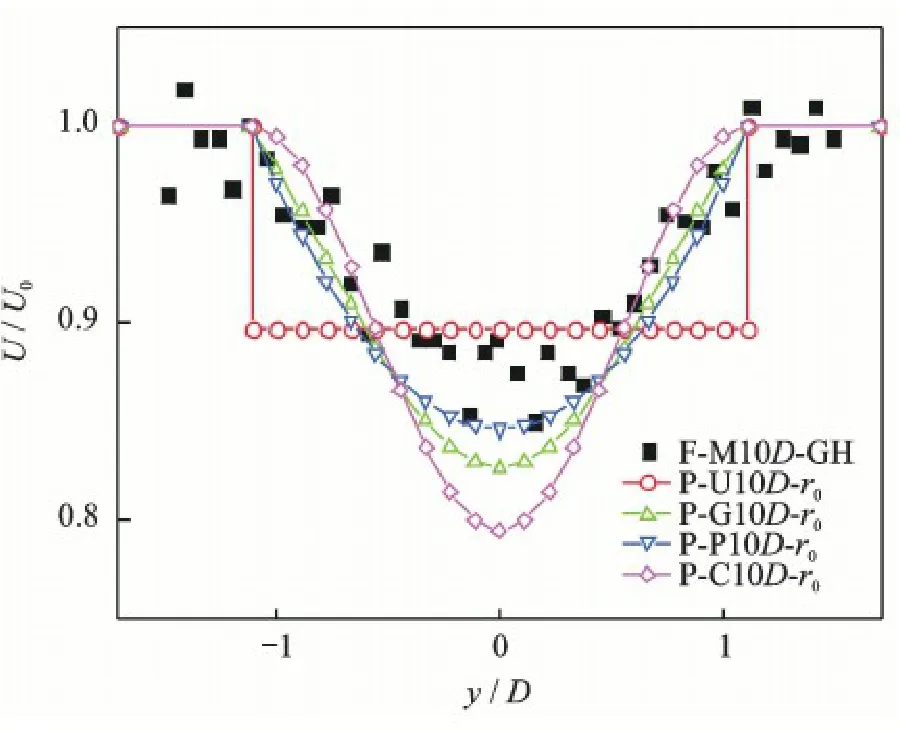
Fig.7　Cross-wind velocity distributions at 10D in the downstream of Garrad Hassan wind turbine

3　Conclusions

Combined with the assumption of the Park model that the wake region is in linear expansion and the cross-wind is in multinomial and Gaussian distribution in the wake region，this paper proposes the modified Park-polynomial model and Park-Gaussian model，to study the wake flow field for a single wind turbine.To further improve the model accuracy，the initial wake radius has been modified.In addition，a comparative analysis has been made with the Park model and the 2D Jensen model.Compared with the measured data of wind farm and the wind tunnel test，it comes to the following conclusions:

(1) The two new modified models (the Parkpolynomial model and the Park-Gaussian model ) could well simulate the wind velocity in the wake region，on account of the fact that the accuracy is approximately consistent with the test result，and the cross-wind distribution conforms to that of the real flow field.Moreover，the two models have inherited many advantages of engineering models，such as simple form，easy-to-code，and high computational efficiency.

(2) The Park-Gaussian model overall performance is the best in all the models，since the precision is superior to other models，and the cross-wind distribution is more consistent with the real flow field under the condition of revised wake radius.

Acknowledgements

This work was funded jointly by the National Basic Research Programof China (″973″Program )(No.2014CB046200)，the Natural Science Foundation of Jiangsu Province (BK2014059)，and the Priority Academic Program Development of Jiangsu Higher Education Institutions.

References:

［1］CLEIJNE J.Results of the Sexbierum wind farm: single wake measurements［R］.TNO Report，1993: 3-76.

［2］OYE S.Tjæreborg wind turbine，first dynamic inflow measurements［R］.Copenhagen: Technical University of Denmark，1991.

［3］TAYLOR G.Wake measurements on the nibe wind turbines in Denmark: ETSU WN5020［R］.Atomic Energy Research Establishment，Energy Technology Support U-nit，1990.

［4］FRANDSEN S，BARTHELMIE R，RATHMANN O.Summary report: The shadow effect of large wind farms measurements data analysis and modeling: Risø-R-1615 (EN)［R］.Roskild，Denmark: Risø National Laboratory，2007.

［5］IVANELL S.Numerical Computations of wind turbine wakes: Elforsk rapport: 09: 27［R］.Stockholm: Royal Institute of Technology，2009.

［6］ALFREDSSON P H，DAHLBERG J A.Measurements of wake interaction effects on the power output from small wind turbine models［R］.Stockholm: FFA，1981.

［7］HAND M M，SIMMS D A，FINGERSH L J.Unsteady aerodynamics experiment phase VI: Wind tunnel test configurations and available data campaigns: NREL/TP-500-29955［R］.Battelle: NREL，2001.

［8］SANDERSE B.Aerodynamics of wind turbine wakes Literature review: ECN-E-09-016［R］.Petten: ECN，2009.

［9］VERMEERA L J，SØRENSEN J N，CRESPOC A.Wind turbine wake aerodynamics［J］.Progress in Aerospace Sciences，2003，39: 467-510.

［10］JENSEN N O.A note on wind generator interaction: Risø-M-2411［R］.Technical report from the Risø National Laboratory，1983: 5-14.

［11］KATÍC I，HOJSTRUP J，JENSEN N O.A simple model for cluster efficiency［C］.［S.l.］: Proceedings from the European Wind Energy Conference，1986: 1-4.

［12］TIAN L L.Numerical simulation of wind turbine wakes and the study of wind farm layout optimization［D］.College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，2014: 61-62.

［13］BARTHELMIE R J，FOLKERTS L，LARSEN G C，et al.Comparison of wake model simulations with offshore wind turbine wake profiles measured by sodar［J］.Journal of Atmospheric and Oceanic Technology，2006，23 (7) : 888-901.

［14］FRANDSEN S.On the wind speed reduction in the center of large clusters of wind turbines［J］.Wind Energy，1992，39: 251-265.

［15］CABEZON D，MIGOYA T，CRESPO A.Comparison of turbulence models for the computational fluid dynamics simulation of wind turbine wakes in the atmospheric boundary layer［M］.John Wiley and Sons，2011: 1-13.

［16］WOLFGANG S，ANDREW T，DAVID Q.GH wind farmer validation report［R］.Garrad Hassan and Partners Ltd，Bristol，2003: 1-32.

Mr.Yang Xiangsheng is a Ph.D.candidate in Nanjing University of Aeronautics and Astronautics (NUAA).His research interests are wind engineering and industrial aerodynamics.

Dr.Zhao Ning is a professor and doctoral supervisor of NUAA，and his research interests lie in numerical methods for fluid dynamics.

Mr.Tian Linlin is studying at NUAA as a Ph.D.candidate and his current research interests include wind engineering and industrial aerodynamics.

(Executive Editor: Zhang Tong)