Hybrid Cartesian Grid Method for Moving Boundary Problems

Shen Zhiwei，Zhao NingCollege of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China (Received 24 October 2015; revised 13 December 2015; accepted 5 January 2016)



Hybrid Cartesian Grid Method for Moving Boundary Problems

Shen Zhiwei，Zhao Ning*
College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China (Received 24 October 2015; revised 13 December 2015; accepted 5 January 2016)

Abstract:A hybrid Cartesian structured grid method is proposed for solving moving boundary unsteady problems.The near body region is discretized by using the body-fitted structured grids，while the remaining computational domain is tessellated with the generated Cartesian grids.As the body moves，the structured grids move with the body and the outer boundaries of inside grids are used to generate new holes in the outside adaptive Cartesian grid to facilitate data communication.By using the alternating digital tree (ADT) algorithm，the computational time of hole-cutting and identification of donor cells can be reduced significantly.A compressible solver for unsteady flow problems is developed.A cell-centered，second-order accurate finite volume method is employed in spatial discretization and an implicit dual-time stepping low-upper symmetric Gauss-Seidel (LU-SGS) approach is employed in temporal discretization.Geometry-based adaptation is used during unsteady simulation time steps when boundary moves and the flow solution is interpolated from the old Cartesian grids to the new one with inverse distance weighting interpolation formula.Both laminar and turbulent unsteady cases are tested to demonstrate the accuracy and efficiency of the proposed method.Then，a 2-D store separation problem is simulated.The result shows that the hybrid Cartesian grid method can handle the unsteady flow problems involving largescale moving boundaries.

Key words:hybrid Cartesian grid; moving boundary; alternating digital tree (ADT) algorithm; unsteady flow

CLC number: V211.3Document code: AArticle ID: 1005-1120(2016)01-0037-08

* Corresponding author，E-mail address: zhaoam@ nuaa.edu.cn.

How to cite this article: Shen Zhiwei，Zhao Ning.Hybrid Cartesian grid method for moving boundary problems［J］.Trans.Nan

jing Univ.Aero.Astro.，2016，33(1) : 37-44.

http: / /dx.doi.org/10.16356/j.1005-1120.2016.01.037

0　Introduction

Computational fluid dynamics (CFD ) for steady flow has already become a practical engineering tool for many different flow problems.However，flows around most fluid machines and living beings involve strong unsteadiness such as flow over wings at large angle of attack，wind turbine aerodynamics，store separation trajectory prediction，and so on.Among the mentioned complicated problems，accurate numerical simulation has difficulties due to the strong unsteady features caused by the large displacement or the quick movement of the wall boundaries.Thus，more efforts are required to improve the efficiency，accuracy and applicability of CFD methods to solve the unsteady flow problems involving moving boundaries.

Several common grid methods have already been developed for moving boundary problems: gridremeshing，dynamicmesh［1］，overset mesh［2-3］，and so on.Grid remeshing method needs to generate new grid cells during every time step，which affects the simulation efficiency dramatically.Dynamic mesh method is simple and easy to be implemented，but it may break down when encountering large-scale movements.Overset Chimera grid method has been proved very powerful for moving boundary problems.In fact，the hybrid Cartesian grid method in the present work belongs to the overset grid method.From the work of Refs.［3-4］，it seems that the most appealing grid topology is a hybrid of Cartesian and viscous layer grids.Following this suggestion，here，a hybrid adaptive Cartesian/Quad grid method is selected for unsteady flow simulation.The near body region is discretized by using a body-fitted structured grid，while the remainingcomputational domain is tessellated with generated Cartesian grids.The Cartesian grid is used for unsteady problems because of the following three reasons:

(1) Solution-based and geometry-based grid adaptations are straightforward to be carried out;

(2) Tree-based data structure can make searching operations efficient;

(3) Grid remeshing would be avoided and the processes of refinement or coarsening of grid cells are performed.

Frequent hole-cutting and donor-cell searching process are necessary to facilitate communications between the structured meshes and the Cartesian meshes during the unsteady moving boundary computations.After a few of time steps，new holes are cut out of the geometry-based adaptive Cartesian grids and new donor cells are identified.Flow solution is interpolated from the old Cartesian grid to the new grid with inverse distance weighting interpolation formula.By using the alternating digital tree (ADT) algorithm［5］，the computational time of hole-cutting and identification of donor cells could be reduced significantly.Compared with other overset grid methods，the overlapped region of the current method is the least and″donor cell″is used to communicate two different grids instead of common interpolated methods.Based on the hybrid grid generation，a compressible solver for unsteady flow problems is developed.A cell-centered，second-order accurate finite volume method is employed in spatial discretization while an implicit dual-time stepping low-upper symmetric Gauss-Seidel (LU-SGS) approach is employed in temporal discretization［6］.

1　Grid Generation

1.1Cartesian grid generation

There are three steps employed to generate the initial hybrid Cartesian grid:

Step 1Generate a body-fitted structured grid by using some commercial software such as Pointwise，ICEM，and so on.The outer boundary is used as the initial interface.

Step 2 Generate the background Cartesian grid to fill computational domain，refine the initial cells which are intersected with the interface until the cell size is matched.

Step 3Cut unnecessary Cartesian cells located in the interface and the hybrid Cartesian/Quad grid is built.

It should be noted that a cut-paste algorithm［7］is used in Step (3)，and this algorithm can also be used for multi-body overlapped grid.When tackling multi-body problems，a preconditioned step is needed to make gap between different structured grids.Two examples are used here to illustrate the basic grid generation algorithm.A single airfoil case and a two-element airfoil case are shown in Fig.1.

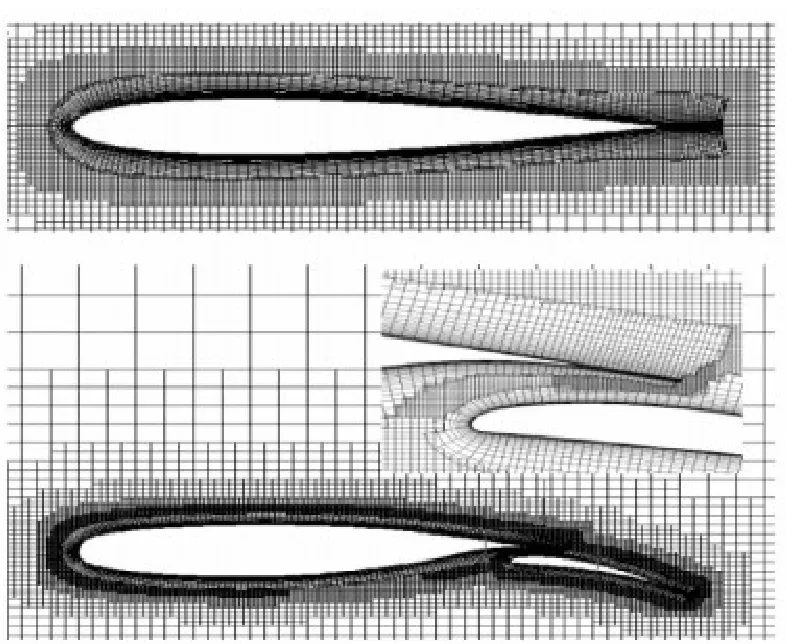
Fig.1　Cases of hybrid Cartesian grid

1.2Identification of donor-cell

Fig.2 is used to describe the identified condition of donor-cell.For the face IJ presented on the structured grid front，a donor-cell is identified from the Cartesian grid block and it should satisfy the next conditions［8］: (1) A set of cells where the unit vector along the line joining face midpoint and cell centroid makes an angle α less than the pre-defined value (30°—50°) with the unit normal n to the face IJ are identified.(2) From this set，a cell centroid J which is closest to the mid-point of face IJ is chosen.

Cell searching should be done frequently during initial grid generation and donor-cell identification.To accelerate these processes，the alternating digital tree (ADT) algorithm is selected.Itcould be found in Ref.［5］for more details about ADT.

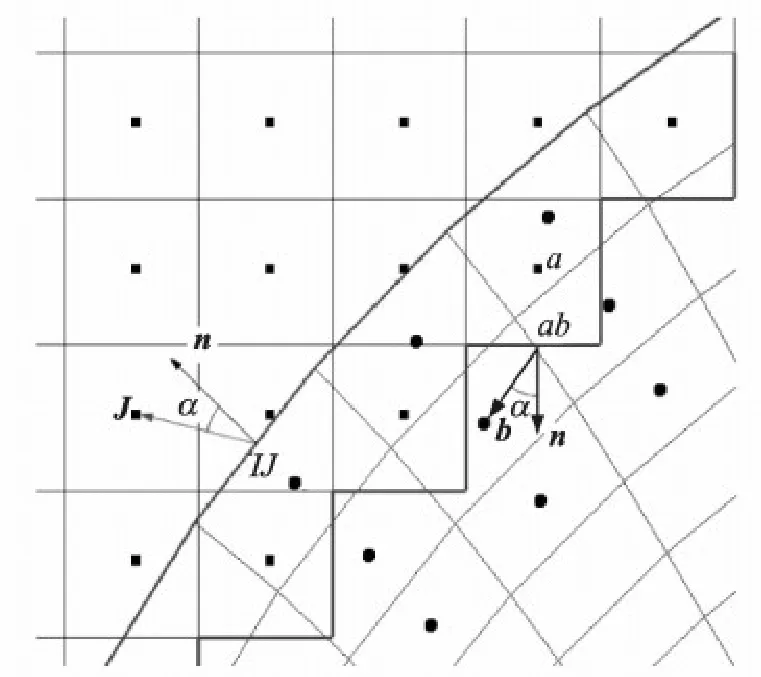
Fig.2　Identification of donor cells

2　Numerical Method

2.1Finite volume method for dynamic grids

The time-dependent Reynolds-averaged Navier-Stokes equations for dynamic grids can be expressed in the integral form as

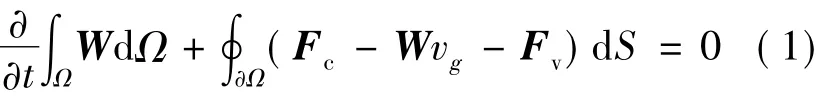
where W is the vector of conservative variables，Fcthe inviscid vector，Fvthe viscous flux vector，and vgthe velocity of mesh.A uniform unstructured data based，cell-centered finite volume compressible solver is developed.The numerical flux is computed by using the advection upstream splitting method + (AUSM + ) scheme，the solution reconstruction procedure is used to obtain secondorder accuracy and the implicit LU-SGS method including the dual time-stepping method is used for the time integration to capture the unsteady phenomena.The two-equation SST k-ω turbulence model［9］is implemented to handle turbulent flows.

2.2Inverse distance weighting interpolation formula

During the unsteady simulation，after a few time steps，the boundary moves to a new position and new Cartesian grid cell appears.In this study，an inverse distance weighting interpolation is used.In Fig.3，the structured grid moves from the red position to the blue position.The Cartesian cell I then is the new appeared one，and its flow value could be interpolated by old Cartesian cells a，b，c，d around itself with the following equation

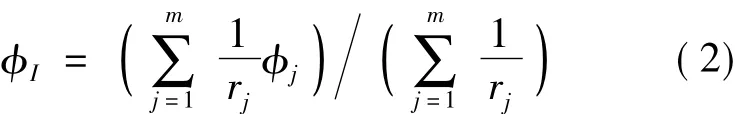
where m refers to a set of cells a，b，c，d and r is the distance between two cells.

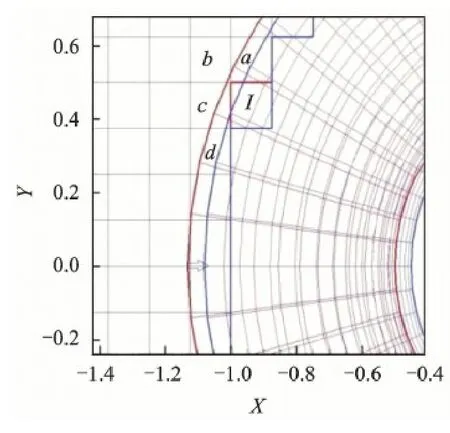
Fig.3　Identification of interpolated cells

3　Conservation and Grid Independence Study

Conservation property is one of the important issues associated with overset grid method.Inviscid subsonic flow past a 5∶3 ellipse in a channel is presented to analyze the conservation of current method.Solid wall boundary condition is imposed on the lower and upper walls while subsonic inlet and subsonic outlet boundary conditions are imposed on the left and right walls.The mass loss η between the inlet and outlet walls are calculated to test the accuracy of this hybrid Cartesian grid method.Three different girds are tested here.Fig.4 shows the coarse grid which has 20×160 structured meshes and 5 582 Cartesian meshes with four mesh refinements.The numbers (nc) of the coarse，medium and fine grids are all listed in Table 1.Fig.5 gives how the mass loss changes when the mesh number increases.With the increase of mesh number，the mass loss is decreased and the value of η could be less than 1.0×10－4with themedium grid.So，it is concluded that mass inflow into the computational domain is almost the same as mass outflow，assuring the conservation property of current method.

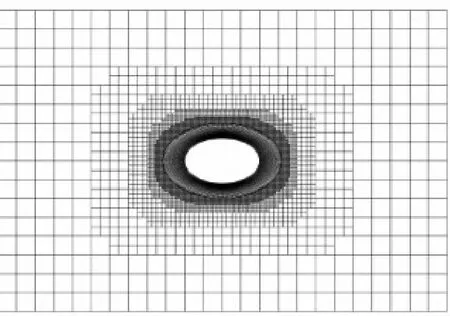
Fig.4　Coarse gird of flow past an ellipse in channel

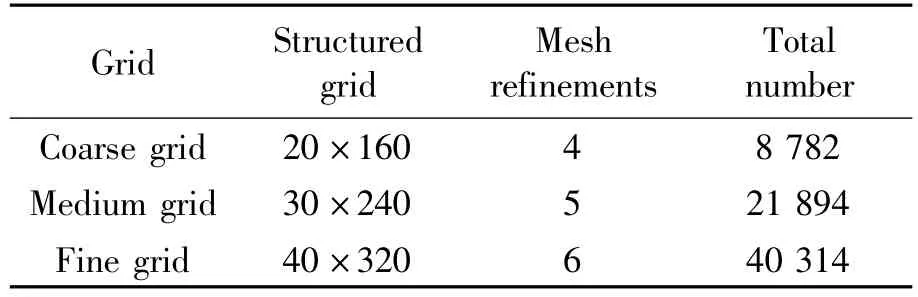
Table 1　Numbers of three different hybrid grids

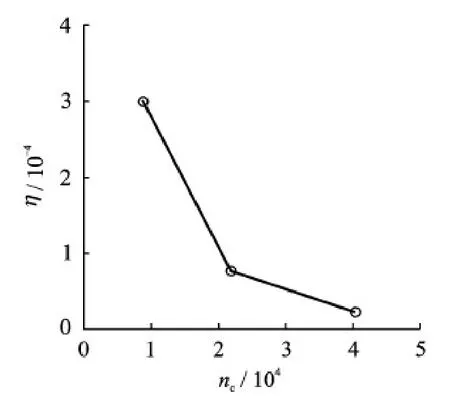
Fig.5　Estimate of mass loss η

4　Results and Discussions

4.1Laminar flow past a rotating cylinder

In the first case，the Mach number and Reynolds number are Ma = 0.30 and Re = 200，respectively while the cylinder is rotating with α= 0.5 (the peripheral-to-translating-speed ratio，α=ω0D /U0)，i.e.，the speed of the cylinder wall is half the translation speed and ω0the angular speed.During the unsteady calculation，the body-fitted structured gird moves with the rotating wall while the outer Cartesian gird does not change.Hole-cutting process is not needed and only donor-cell identification is needed.In the region of wake development，the Cartesian gird has been refined and mesh details are shown in Fig.6，including 9 000 body-fitted structured grid cells and 18 768 Cartesian grid cells.

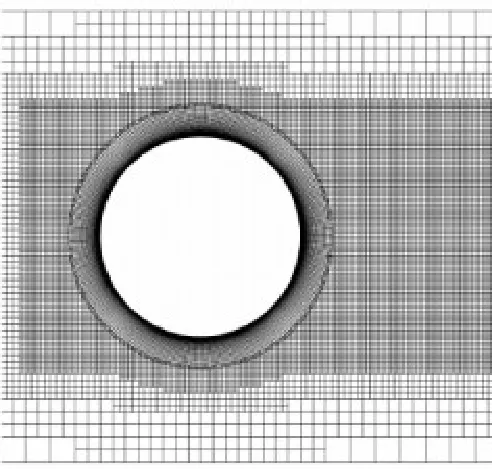
Fig.6　Initial mesh details around cylinder

The computational results of wake development behind an impulsively started translating and rotating circular cylinder are compared with experimental results by Madeleine and Christian［10］.Wake streamlines at four different normalized times，T =1.0，T = 2.5，T = 4.0，T = 5.5，are presented in Fig.7 and good agreement can be found between the present result and the experimental result.Then the evolution of U/U0along the flow axis X at different times is examined.From Fig.8，it shows that our results agree well with the experiment results at time T =1.0，1.5，2.0，3.0.

4.2Turbulent flow over oscillating NACA0012 airfoil

The case of turbulent flow over oscillating NACA0012 airfoil is a viscous turbulent flow problem.The flow parameters are Ma = 0.60 and Re = 4.8×106.The airfoil oscillates along the following expression:α=αm+α0sin(ωt)，here，αm= 4.86°，α0= 2.44°，and k =ωc/(2U∞) = 0.081.The axis of the motion is located on 0.25c.The unsteady computation starts from the converged steady result.The initial mesh contains 12 600 structured cells and 2 818 Cartesian cells.With the motion of body-fitted grid，the hole-cutting and donor-cell searching processes are needed at every time step.Then 180 time steps are used for each cycle to capture the unsteady features.Fig.9 displays the computed Mash number contours when α= 6.97°increases and α= 2.43°decreases.In Fig.10，the pres-sure coefficient (Cp) distributions along the airfoil surface at four typical angles of attack are displayed.Fig.11 shows the time history of the lift coefficient.Both results show good agreement with the experimental results［11］.

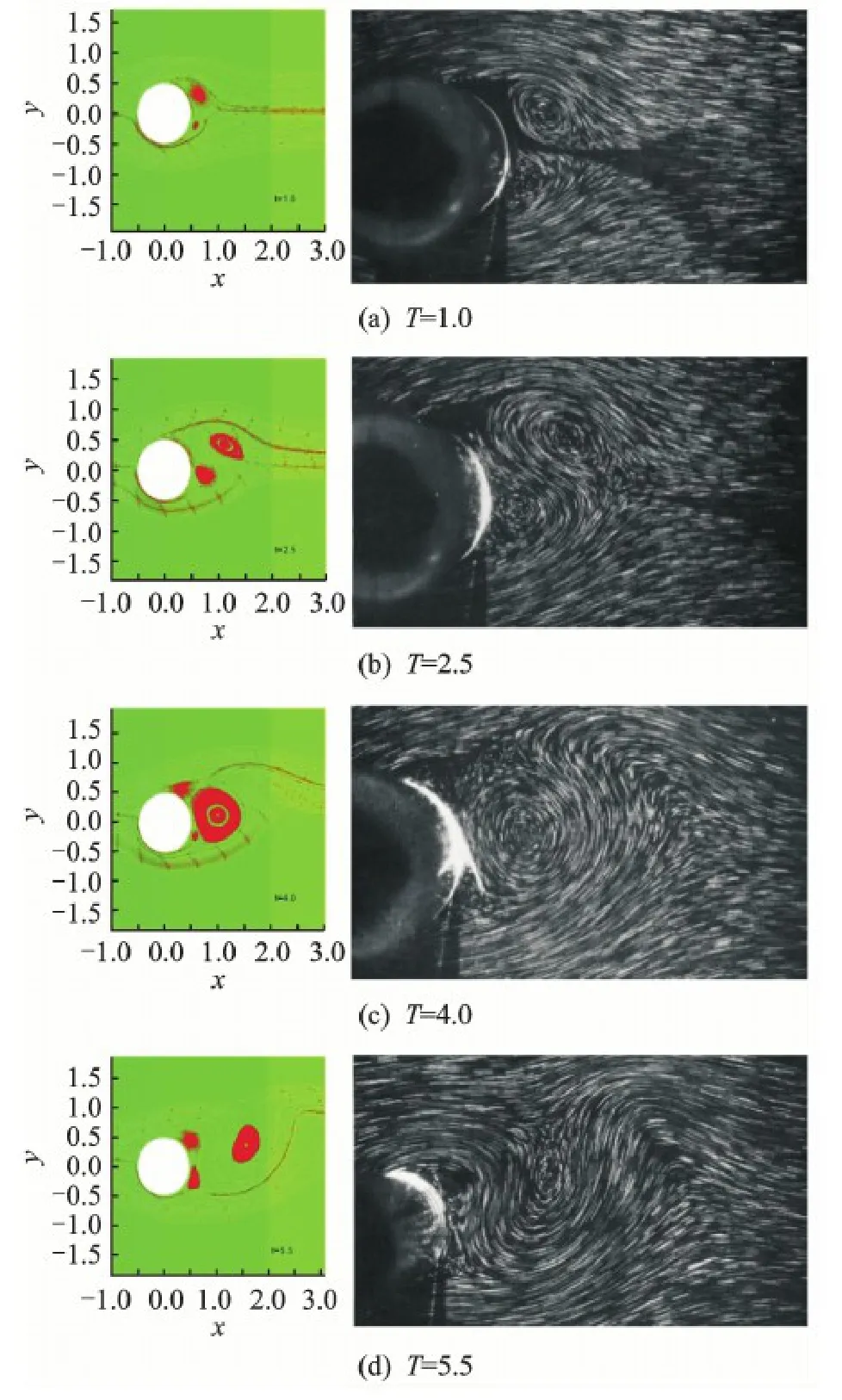
Fig.7　Computed streamlines and experimental results at different time during wake development

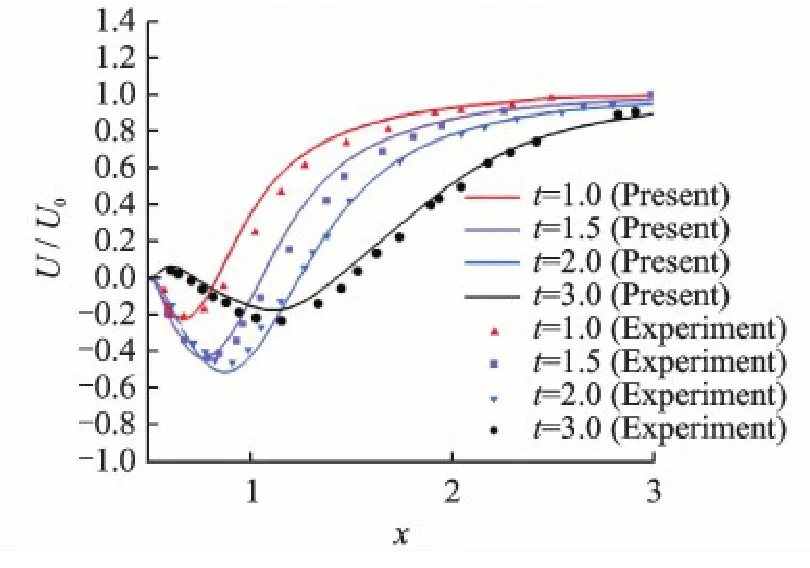
Fig.8　Evolution of U/U0along the flow axis x at t =1.0，1.5，2.0，3.0

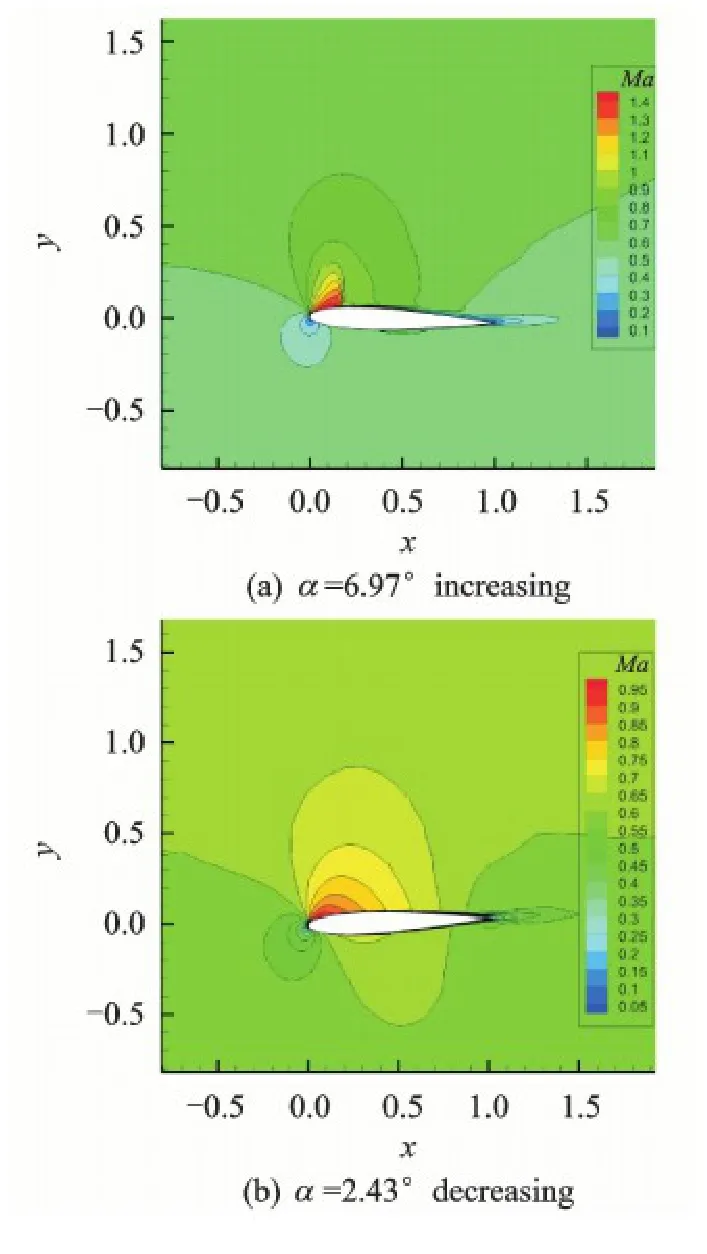
Fig.9　Mach number contours when α=6.97° increases and α=2.43°decreases

4.3Prediction of 2-D store separation problem

The last case considers the prediction of a 2-D store separation problem.The fluid dynamics and rigid-body dynamics equations are coupled here to simulate the free fall of the 2-D store after separation from a wing section.In Ref.［12］，the non-dimensional moment of inertia I equals to 2.45 and the non-dimensional mass m equals to 63.206.To compare the results，both geometry size and flow parameters keep the same with this reference，Ma = 0.60，α= 0.0 and the governing equations being the Euler equations.Initial mesh details are shown in Fig.12，in our initial time step，there contains 4 500 structured cells around the NACA64A010 wing section，4 500 structured cells around the store and 16 989 outside Cartesian grids.We start the fall simulation after 5 000 steady calculations and set unsteady time step Δt = 0.05.Fig.13 displays the pressure contours when t =0.0 and t =3.0.Fig.14 shows the time history of aerodynamic coefficients (lift: CL，drag: CD，moment: CM) and we compare them with the results of Ref.［12］.Good agreement shows that our method can predict the 2-D store separation accurately.

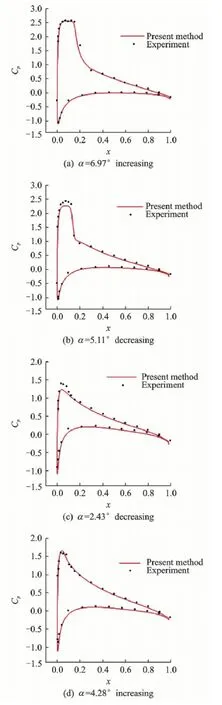
Fig.10　Cpdistributions along airfoil surface at four typical angles of attack

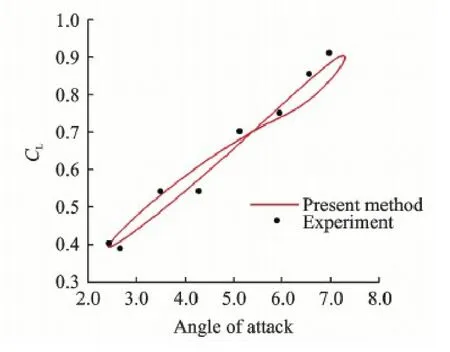
Fig.11　Time history of lift coefficient

Fig.12　Initial mesh details

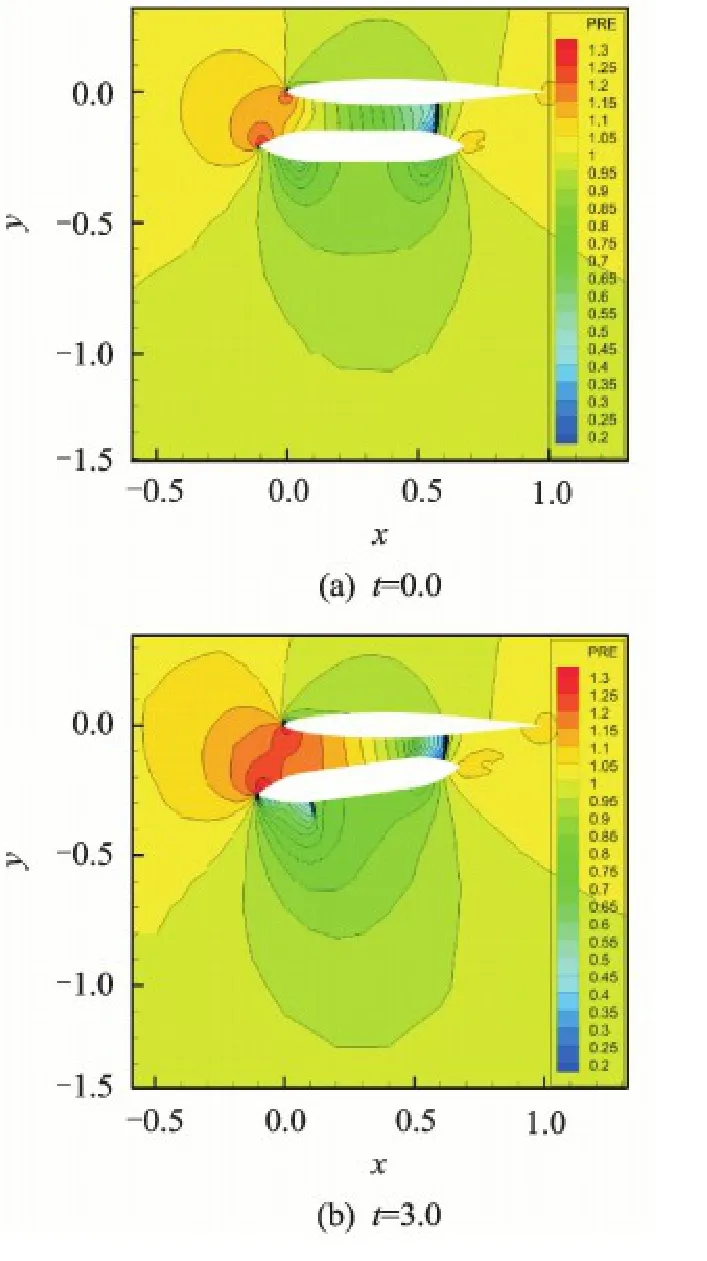
Fig.13　Pressure contours at t =0.0　and t =3.0　during store separation (m =63.206，I =2.45)

Next，we change the values of m and I (m = 189.618，I = 49.0) and keep other conditions the same.In this condition，simulation starts from 5 000 steady steps and ends until t =30.From the following three different pressure contours (t = 0，t = 15，t =30) in Fig.15，it can be found that large-scale movement appeared and the proposed method keeps effective under this condition.

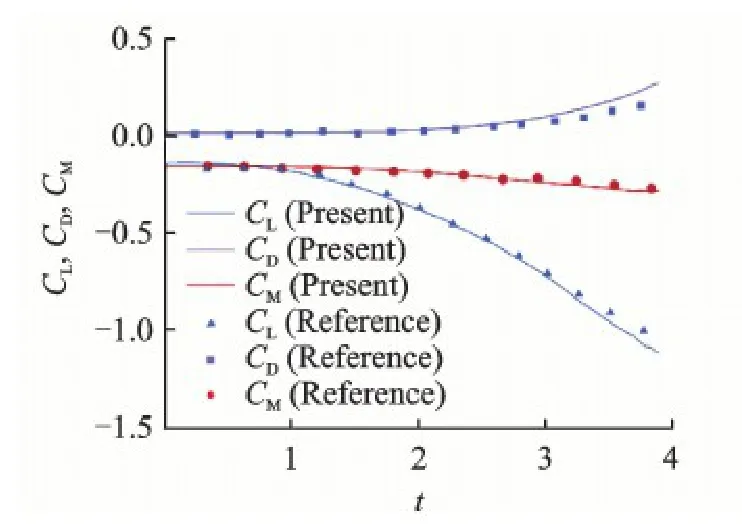
Fig.14　Time history of aerodynamic coefficients

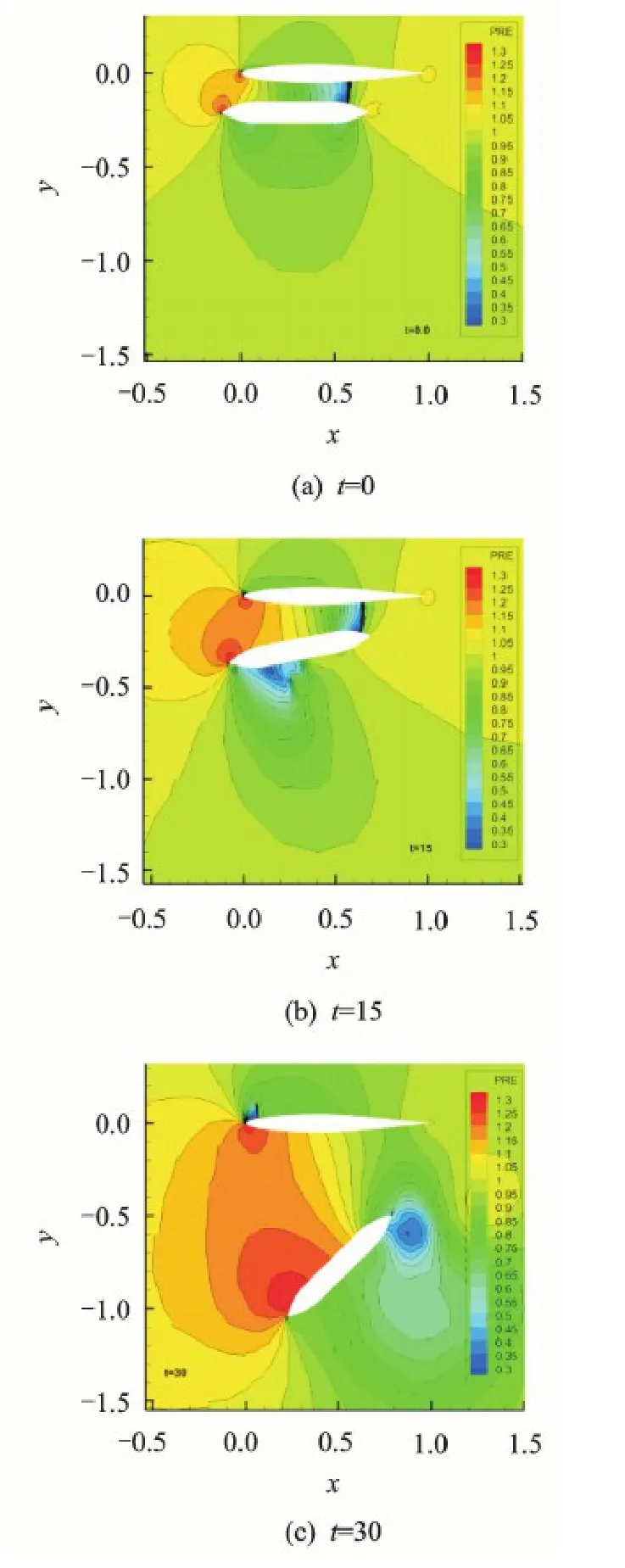
Fig.15　Pressure contours at t =0，15，30　during store separation (m =189.618，I =49.0)

5　Conclusions

From 2-D cases for both laminar and turbulent unsteady flow simulations，as well as the simulation of 2-D store separation problem，the computational results show good agreement with the experimental data or results from other references.The accuracy of the present hybrid Cartesian grid method and the ability of handing large-scale moving boundary problems are both demonstrated.For the future work，we try to extend the proposed method to 3-D unsteady flow problems，such as wind turbine aerodynamics，helicopter rotor problems，and so on.

Acknowledgement

This work was supported partly by the National Basic Research Programof China (″973″Program )(No.2014CB046200).

References:

［1］HADIDOOLABI M，JAHANGIRIAN A.An implicit central difference method for solution of three dimensional unsteady aerodynamics on unstructured moving grids: AIAA 2005-5257［R］.［S.l.］: AIAA，2005.

［2］CHEN R F，WANG Z J.Fast block lower-upper symmetric Gauss-Seidel scheme for arbitrary grids［J］.AIAA Journal，2000，38(12) : 2238-2245.

［3］RAVISHEKAR K，WANG Z J.Overset adaptive Cartesian/Prism grid method for stationary and movingboundary flow problems［J］.AIAA Journal，2007，45 (7) : 1774-1778.

［4］ZHANG L P，WANG Z J.A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamics meshes: AIAA 2003-3886［R］.［S.l.］: AIAA，2003.

［5］BONET J，PERAIRE J.An alternating digital tree (ADT) algorithm for 3D geometric searching and intersection problems［J］.International Journal for Numerical Methods in Engineering，1991，31(1) : 1-17.

［6］BLAZEK J.Computational fluid dynamics: Principles and applications［M］.Amsterdam: Elsevier，2001.

［7］CHO K W，KWON J H.Development of a fully systemized chimera methodology for steady/unsteady problems ［J］.Journal of Aircraft，1999，36(6) : 973-980.

［8］MUNIKRISHNA N，LIOU M S.A Cartesian based body-fitted adaptive grid method for compressible viscous flows: AIAA 2009-1500［R］.［S.l.］: AIAA，2009.

［9］MENTER F R.Two-equation eddy-viscosity turbulencemodels for engineering applications［J］.AIAA Journal，1994，32(8) : 1598-1605.

［10］MADELEINE C，CHRISTIAN M.Influence of rotation on the near-wake development behind and impulsively started circular cylinder［J］.J Fluid Mech，1985，158: 399-446.

［11］LANDON H.Compendium of unsteady aerodynamic measurements［R］.AGARD Report，1983: 1983-702.

［12］PU S H，CHEN H Q.Hybrid cartesian grid/gridless method for solving moving boundary problems［J］.Journal of Nanjing University of Aeronautics and Astronautics，2010，42(4) : 477-482.(in Chinese)

Mr.Shen Zhiwei is a Ph.D candidate of Nanjing University of Aeronautics and Astronautics (NUAA).His research interests are computational fluid dynamics.

Dr.Zhao Ning is a professor and doctoral supervisor in NUAA and his research interests focus on computational fluid dynamics.

(Executive Editor: Zhang Tong)