Vector Dominating Multi-objective Evolution Algorithm for Aerodynamic-Structure Integrative Design of Wind Turbine Blade

Wang Long，Wang Tongguang，Wu Jianghai，Ke ShitangJiangsu Key Laboratory of Hi-Tech Research for Wind Turbine Design，Nanjing University of Aeronauticsand Astronautics，Nanjing 210016，P.R.China(Received 18 August 2015; revised 20 December 2015; accepted 5 January 2016)



Vector Dominating Multi-objective Evolution Algorithm for Aerodynamic-Structure Integrative Design of Wind Turbine Blade

Wang Long*，Wang Tongguang，Wu Jianghai，Ke Shitang
Jiangsu Key Laboratory of Hi-Tech Research for Wind Turbine Design，Nanjing University of Aeronautics
and Astronautics，Nanjing 210016，P.R.China
(Received 18 August 2015; revised 20 December 2015; accepted 5 January 2016)

Abstract:A novel multi-objective optimization algorithm incorporating vector method and evolution strategies，referred as vector dominant multi-objective evolutionary algorithm (VD-MOEA)，is developed and applied to the aerodynamic-structural integrative design of wind turbine blades.A set of virtual vectors are elaborately constructed，guiding population to fast move forward to the Pareto optimal front and dominating the distribution uniformity with high efficiency.In comparison to conventional evolution algorithms，VD-MOEA displays dramatic improvement of algorithm performance in both convergence and diversity preservation when handling complex problems of multi-variables，multi-objectives and multi-constraints.As an example，a 1.5 MW wind turbine blade is subsequently designed taking the maximum annual energy production，the minimum blade mass，and the minimum blade root thrust as the optimization objectives.The results show that the Pareto optimal set can be obtained in one single simulation run and that the obtained solutions in the optimal set are distributed quite uniformly，maximally maintaining the population diversity.The efficiency of VD-MOEA has been elevated by two orders of magnitude compared with the classical NSGA-II.This provides a reliable high-performance optimization approach for the aerodynamic-structural integrative design of wind turbine blade.

Key words:wind turbine; multi-objective optimization; vector method; evolution algorithm

CLC number: TM614Document code: AArticle ID: 1005-1120(2016)01-0001-08

* Corresponding author，E-mail address: longwang@ nuaa.edu.cn.

How to cite this article: Wang Long，Wang Tongguang，Wu Jianghai，et al.Vector dominating multi-objective evolution algorithm for aerodynamic-structure integrative design of wind turbine blade［J］.Trans.Nanjing Univ.Aero.Astro.，2016，33(1) : 1-8.

http://dx.doi.org/10.16356/j.1005-1120.2016.01.001

0　Introduction

The design of large-scale wind turbine blade relies on the best match of all parts of the whole machine，and therefore cannot be considered as a singlecomponent optimization problems.This means that the design is a complicated optimization problem involving many variables，objectives and constraints，such as the maximum power output，the minimum machine cost，the minimum tower load，control requirement，noise reduction and good manufacturing process，etc.，among which conflicts may exist［1］.In normal conditions，it is very difficult to solve this kind of coupling problems with conventional hierarchical decoupling methods［2-3］.In multi-objective optimization，there is no single solution that is optimal (global minimum or maximum) with respect to all the optimization objectives in contrast to single-objective one.Only acceptable non-dominated solutions exist，i.e.，the so-called Pareto optimal solutions.Currently on engineering，an trial-and-error design process as ″aerodynamic design—structural design—verification—improvement″is usually adopted in wind industry，where the blade aerodynamic design and structural design are separated，and the coordination of the multi-variables，multi-objectives and multi-constraints relies on engineering experience; so much so that a feasible solution instead of an optimal solution can only be obtained and it may not match the wind turbine system the best.

Theoretically，the aerodynamic and structural coupling design is the best choice to handle such issues by means of multi-objective optimization meth-ods［4-6］.However，wind turbine operates in a complex circumstance，and therefore thousands of design load cases (DLCs) need to be evaluated according to the design standards，resulting in such a huge computational overhead that optimal efficiency becomes one of the key indicators to be considered.In addition，wind turbine design is a non-linear，non-decoupling and constrained multi-objective optimization problem，for which there exist a large number of optimization objectives，variables and constraints with the presence of complex links and restrictions among them.These two challenges put forward strict requirements for the multi-objective optimization algorithm in both convergence and efficiency.

Over the past decades，rapid progress in multiobjective optimization has been made.Some classical methods such as normal boundary intersection (NBI)［7］and normal constraint (NC)［8］constructs a linear reference plane on which a series of uniform distribution points are arranged with a form of regular simplex structure.Based on such ideas，the methods are able to obtain Pareto optimal solutions of uniform distribution.But the main drawback is that a complete single-objective optimization process needs to be carried out for every point obtained from Pareto optimal solutions，which makes the design process quite computationally expensive and the resulted calculation amount usually unbearable.Multi-objective evolution algorithms (MOEAs )，such as NSGA-II［9］，SPEA2［10］and HypE［11］，deriving the whole Pareto optimal set by launching only one single simulation run，is very attractive to designers.But when they are used to deal with complex or high-dimensional problems，difficulties or failures in diversity preservation，low-efficiency，poor-convergence and other issues become too challenging to overcome.Consequently，multi-objective optimization algorithm has become a key factor to restrict the aerodynamic-structural integrated design of wind turbine blade.

In this paper，a new multi-objective optimization algorithm incorporating vector method and evolution strategies is proposed，followed by its critical operators and algorithm procedures to be described elaborately.As an example，the design of a 1.5 MW wind turbine blade is accomplished and analyzed to investigate the basic features of the algorithm.The performance of the new algorithm is also provided by comparison with the classical algorithm.

1　Vector Dominant MOEA

In this section，a new multi-objective evolutionary algorithm characterized by vector projection and vector diversity preservation in order to improve the efficiency and convergence is presented，named the vector dominant multi-objective evolutionary algorithm (VD-MOEA).This algorithm retains the basic frameworks of evolution algorithm and in particular constructs a Utopia reference system consisting of anchor points，Utopia plane，Utopia plane points and Utopia vectors，similar to the traditional NBI and NC methods.In VD-MOEA，population individuals are firstly related to Utopia vectors one by one，then are guided to advance along the vector directions，and finally converged to the intersections of the projection vectors and the Pareto optimal front.The procedures and main operator introduction of VD-MOEA are described as follows:

(1) Parameter input: Define the size of algorithm population NPand external archive population NE.Set maximum iteration number T.Set upper and lower bounds for the variables one by one.

(2) Utopia reference system construction: Define the divisions of each objective axe NS.Construct Utopia reference system in normalized M-dimensional space including anchor points，Utopia plane，Utopia points and Utopia vectors(Fig.1).Utopia points uiare a set of evenly spaced points generated by reasonably schematizing weight vectors w，given by

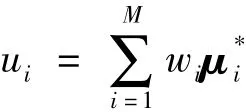
where

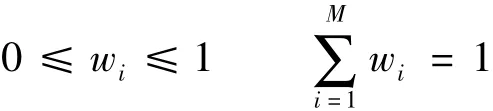
The total number of Utopia points NUin an M-objective optimization space can be calculated by

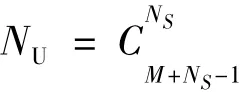
(3) Population initialization: Generate initial population P0.Evaluate the fitness value of all individuals in P0.Copy all individuals of P0to the exter-nal archive population PE.

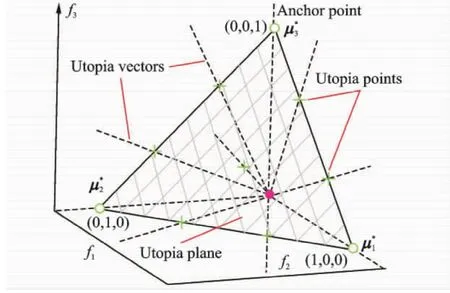
Fig.1　Normalized Utopia reference system for a three objective case

(4) Genetic and evolutionary operation: Carry out neighborhood selection，simulated binary crossover (SBX) and polynomial mutation to the external archive population PE.Generate the next generation Pt.

(5) Population recombination: Evaluate fitness and constraint values of each individual in the population Pt.Generate the combined population Qtby mixing current population and external archive population，expressed as

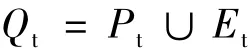
Therefore，the size of the combined population is 2NP.

(6) Strengthnon-dominateddelamination: Strength non-dominated delamination strategy in the algorithm originates from SPEA2 where each individual in the combined population is compared with other individuals on the basis of the strength Pareto optimal principles to find Pareto non-dominated rank.Thus the Pareto optimal solutions of the tth generation are identified and of which every individual is assigned to a Pareto non-dominated rank.

(7) Population fitness normalization: Analyze the Pareto optimal solutions from the combined population Qtto find the minimum and maximum fitness in every objective direction，and then make up the Nadir point fNand Utopia point fU.For the individual i，its original fitness fi(x) is transformed to the dimensionless fitness Fiby adopting the following formula

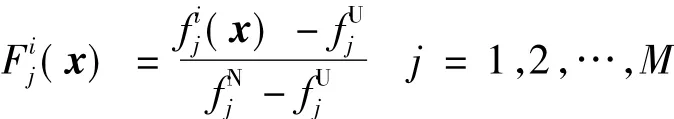
Accordingly，the combined population Qtcan be normalized as the new combined population.

(8) Association operation: Until now，Utopia vectors and normalization populationhave been completely built.In this step，the association operation that each member ofis classified and subordinated to a vector is launched.For the purpose，the Euclidean distance of each individual ofwith each of the vectors is calculated，and a vector is then found to be associated with every individual according to the shortest distance rule.After finishing this process，every vector has a subset Za(j) normally including one or more members.

(9) Aggregation fitness assignment: Each individual ofincludes three key parameters，i.e.，Pareto non-dominated rank (PR)，Euclidean sorting (ES) ranking according to the Euclidean distance in subset Za(j) of the associated vector，and reference number (RN).Based on these，a new fitness assignment method defined by serial connection with PR，ES and RN is proposed，named the aggregation fitness.Thereby，the aggregation fitness of an individual is expressed as

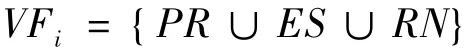
The aggregation fitness artfully forms a real value that can be used for comparison between each other，well preparing for the upcoming elite preservation and parent selection for the next generation.

(10) Elite preservation strategy: All individuals in Qtare sorted in an ascending order according to the aggregation fitness，and frontal NEindividuals are truncated to the external archive population forming a new generation.

(11) Termination: If t＞T or other stopping principles are satisfied，storage the external archive population as the ultimate optimal solutions; otherwise，set t = t +1，go back to step (4) and continue iteration process of the next generation.

2　Optimization Models of Wind Turbine Blade

2.1Design variables

The design variables of wind turbine blade can be divided into two parts: aerodynamic configuration variables and structural layout variables.The aerodynamic configuration variables are used to describe the blade geometrical features of the distributions of the chord，twist，thickness and so on，which determinethe blade aerodynamic performance and fulfills the engineering manufacture requirements.In this design，a group of three-order polynomials defining nine variables are adopted，which are able to represent all common-used blade shape.

In the engineering application，the number of structural layout variables usually is so large dozen that must be simplified on the basis of engineering experience as much as possible for lightening the burden of optimization.In the work，we fix the relative positions of blade spar，web，and trailing edge enhanced layer and so on for simplification，and twelve structural design variables are defined to optimize their thickness.

2.2Optimization objectives

In this paper，maximum annual energy production (AEP)，minimum blade mass，and minimum root thrust，among which distinct conflicts exist，are chosen as three optimization objectives to validate the developed optimization algorithm.

(1) Maximum AEP

The AEP of wind turbine blade relating to recovery of the cost rate is the main design goal.Annual energy generation is calculated under the given wind farm conditions as follows

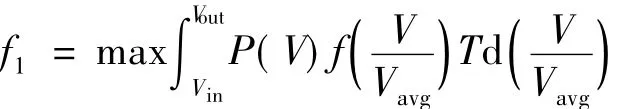
where Vinand Voutare the cut-in and cut-out wind speeds，respectively.Vavgis the annual average wind speed，P(V) the output power at the wind speed V，f the Weibull distribution function，and T the annual hours.

The modified blade element momentum (BEM) theory is used in calculation of the AEP.The modifications include the tip loss，the hub loss，and correction of the axial induced velocity factor at large thrust state.

(2) Minimum blade mass

The basic blade structure is primarily made up of double web I-beam，as shown in Fig.2.The material used for the bulk of the blade is glass fiber with reinforced polyester and PVC foam.

To obtain blade mass，mass distribution of the blade is firstly calculated by the applied classic beam theory.The total mass of the blade is then calculated by integration as follow

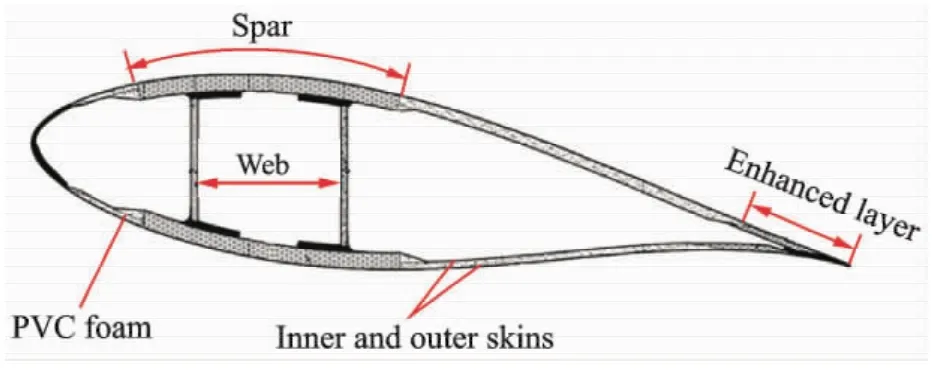
Fig.2　Blade structure schematic

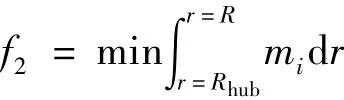
where Rhubis the hub radius，R the radius of wind rotor，and mithe mass per unit spanwise length at the ith section.

(3) Minimum root ultimate thrust

After finishing all the calculation of every design load conditions (DLC) according to the GL guideline，the objective function for minimum root ultimate thrust is as follows

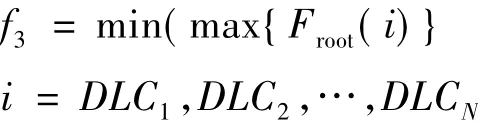
where Froot(i) is the blade root load of the ith DLC.

3　Optimization Design of 1.5　MW Wind Turbine Blade

In this section，a three-objective design of 1.5 MW wind turbine blade employing the maximum AEP，the minimum blade mass，and the minimum blade root thrust as the optimization objectives is presented.The blade design relies on a wind turbine platform of upwind，variable speed and variable pitch，doubly-fed generator.The blade length of 40.3 m，design grade of 3A，rated rotational speed of 17.4 r/ min are selected as a design basis，and the other basic parameters are given in Table 1.Also，the blade introduced in this section for the purpose of comparison is a counterpart blade，Aerodyn-1.5 MW blade，with its AEP of 5 828.2 MWh/a，blade mass of 5 943 kg and root thrust of 162 kN，respectively.

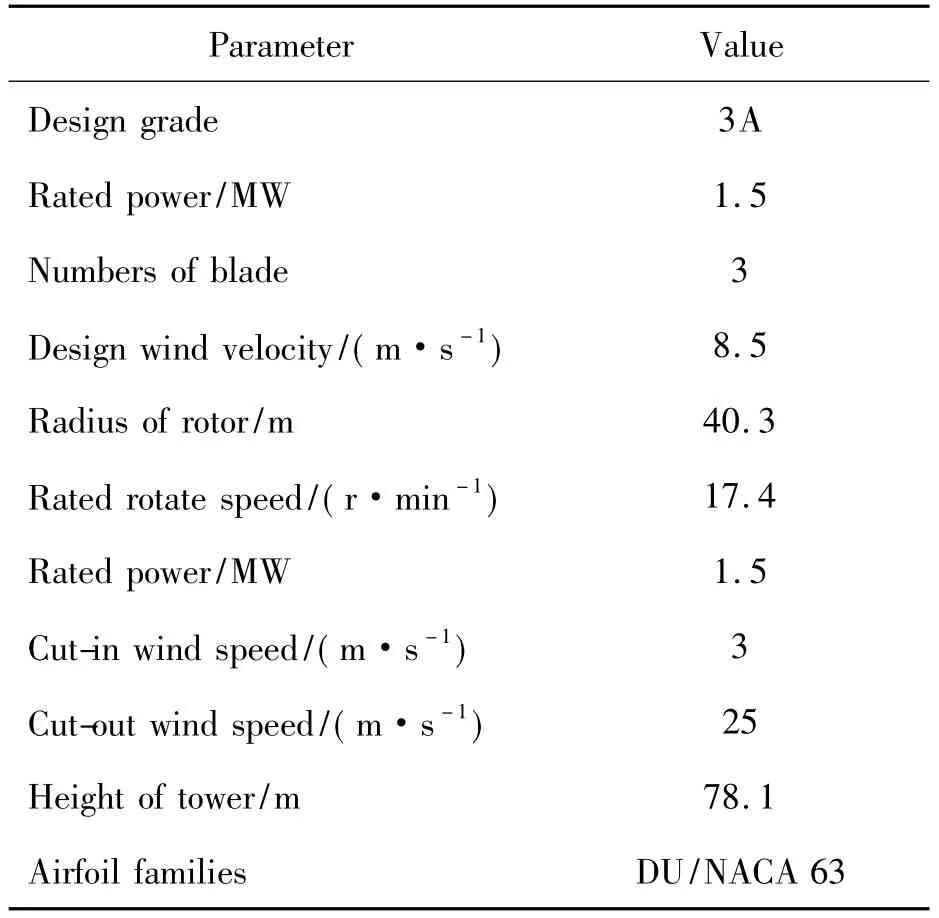
Table 1　Basic parameters of wind turbine

Fig.3(a) shows the Pareto optimal solutions and distributions that meet the maximum AEP (f1)，the minimum blade mass (f2) and the minimum root thrust (f3) of the wind turbine simultaneously.In this design，the maximum iterations are set as 200，the divisions of each objective axe NSare prudentially defined as 11 to get a balance between convergence and efficiency，and thus the population size is calculated to be 78.The auxiliary surface to which the optimal solutions are attached in Fig.3 is fitted using five-order polynomial functions.It can be seen that the Pareto optimal solutions constitute a continuous curved surface with evident boundaries and complicated polygon characteristics，which are formed under the comprehensive influences of the variables，objectives and constraints.The optimal solutions in three-dimensional space achieve good convergence and their distribution is very uniform，meaning that the performance of VD-MOEA in the multi-objective optimization of wind turbine blade is excellent.Fast convergence can be achieved even in the case of small population.All the points in the Pareto optimal set are the optimal solutions for the design conditions，and no one is superior to the others.With a set of optimal solutions，the multi-objective optimization design provides more flexible selections for designers than the conventional scheme of a single optimal solution.

For comparison，another group of Pareto optimal solutions obtained using the conventional NSGA-II under the same design conditions are displayed in Fig.3 (b).The population size and optimization iterations are set as 500 and 2 000 respectively on the basis of the practical experience.It can be seen that the geometrical shapes of the different optimal solutions provided by the VD-MOEA and NSGA-II seem to be quite similar.Although the optimal solutions from NSGA-II is more in number，but their distributivity is relatively poor，mainly concentrated in the boundary line，especially the individuals are much fewer in the middle part of the optimal front.The key reason of this phenomenon is that the uniformity diversity preservation strategy of NSGA-II is not embodied，which is a significant deficiency.Moreover，it is also clear that the optimization efficiency of VD-MOEA has been elevated by two orders of magnitude in comparison to classical NSGA-II，and the competitive advantage in distributivity of the optimal solutions is more remarkable.

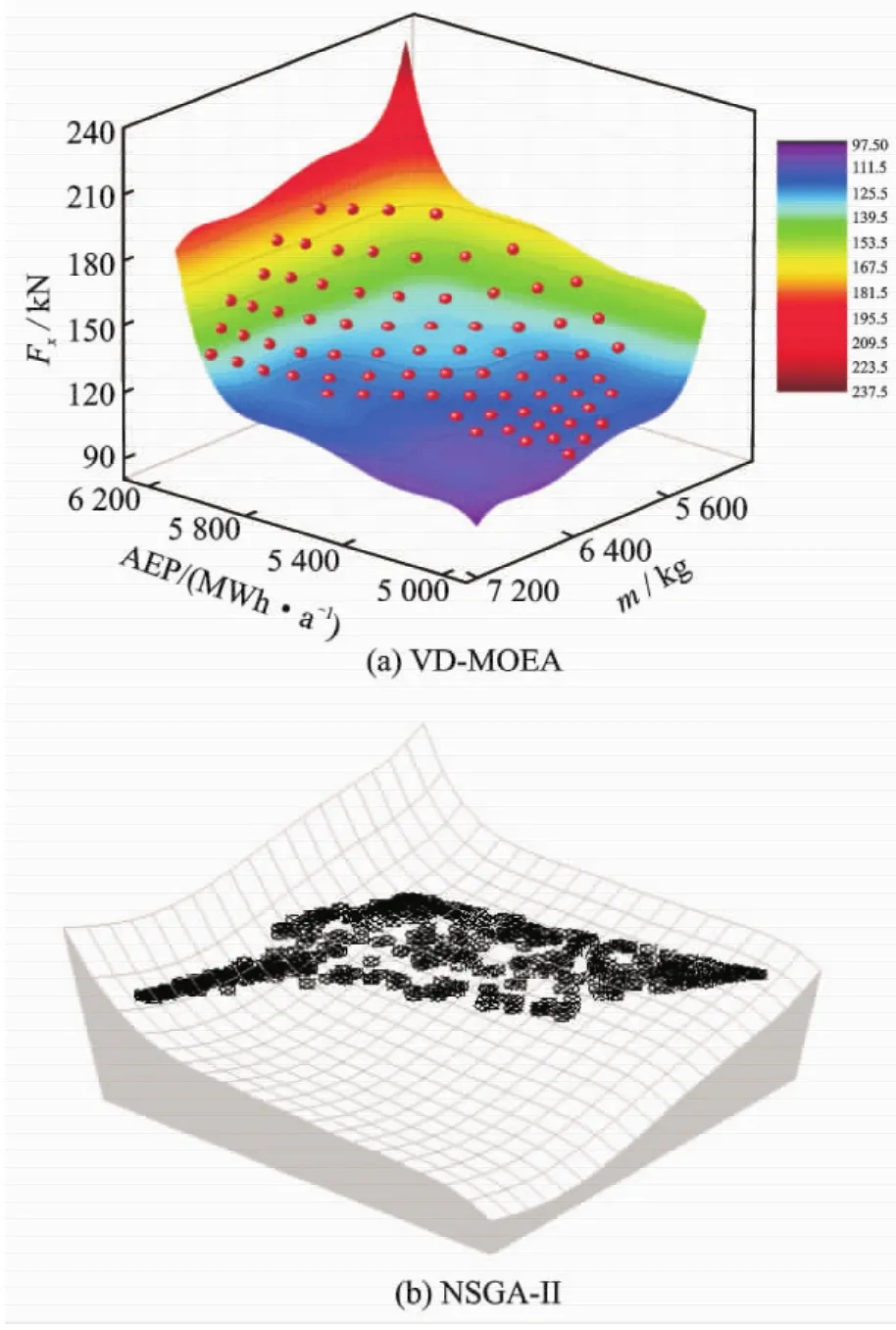
Fig.3　Distribution of Pareto optimal solutions in three-dimensional space

For clarity，the distribution of Pareto optimal so-lutions obtained using VD-MOEA is projected to the two-dimensional planes of f1-f2and f1-f3presented，as shown in Fig.4.The solutions are also found satisfactorily spreading and uniform in the two-dimensional space.

To better illustrate the features of Pareto optimal front，three blade designs marked in Fig.4 are selected to be analyzed.The AEPs，masses and ultimate root thrust of the blades A，B，C as well as the counterpart blade are listed in Table 2，respectively.Let us look at the blades A and B firstly.The AEP of Blade A is a little higher than that of Blade B just by about 1.6% and，correspondingly，the root thrust of Blade A is a little higher than that of Blade B just by about 2.0%.From common point of view，it seems that Blade A should be heavier than Blade B.From the multi-objective optimization design，however，the mass of Blade A is lower than that of Blade B by a margin of about 5.4% on the contrary.To explain the causes of forming this kind of complex objective combinations，there is not yet enough information acquired just from Figs.3，4This is only made by additional comparison of aerodynamic characteristics of different blade designs.Fig.5 shows the distributions of chord，relative thickness and absolute thickness for these three blades.From Fig.5，the solidity of Blade A is obviously larger than that of Blade B，which produces increased load of Blade A.This is the main reason why the root thrust and AEP of Blade A are a little larger.However，it can be seen from Fig.5 that the relative thickness of blade B is lower and therefore has a higher lift coefficient，thus resulting in both higher aerodynamic performance and higher thrust.By these compromises， the differences in both AEP and blade mass between Blades A and B are not remarkable.Meanwhile，because Blade A has higher stiffness owing to a larger absolute thickness resulted from thicker airfoil and wider chord，it may need the thinner bearing layout to resist the load and meet the deflection constraints，and thus the blade mass is effectively reduced.

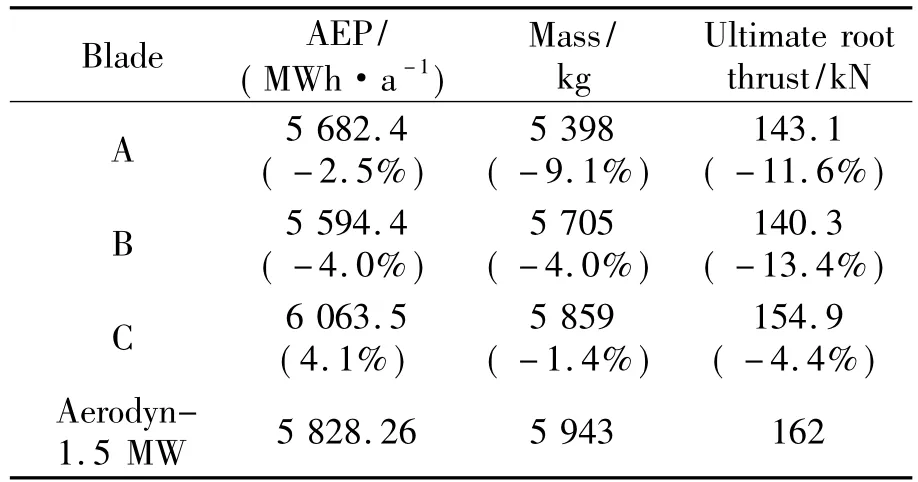
Table 2 Performance comparisons of the different blades

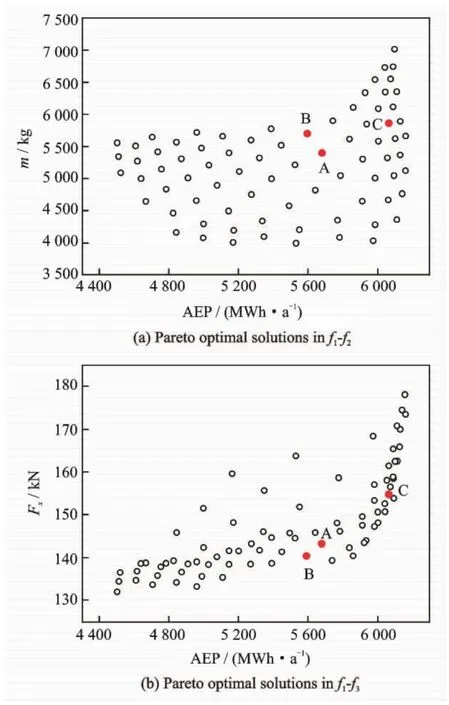
Fig.4　Pareto optimal solutions in the two-dimensional projection space

Blade C produces higher AEP than Blade B because the chord of Blade C is wider than that of Blade B.On the other hand，the absolute thickness of Blade C is larger than that of Blade B，which is helpful to decrease the blade mass.The relative thickness of Blade C is the least among the three designs，which is also beneficial to improve the aerodynamic efficiency，resulting in the highest AEP.In summary，the AEP，mass，and root ultimate thrust cannot simultaneously be optimal.Nevertheless，good blade aerodynamic performance is generally acquired at the cost of high load on the blade，thus resulting inblade mass increase.By comparing Blades A，B and C，as well as Aerodyn-1.5 MW blade (5 828.2 MWh/a，5 943 kg and 162 kN)，it can be seen that the AEP，mass，and root ultimate thrust of Blade C are increased by 4.1%，－14% and－4.4%，respectively，than the Aerodyn-1.5 MW blade，demonstrating that Blade C has good performance in all the three-objective directions and seems to be a more desirable result than the other two blades.

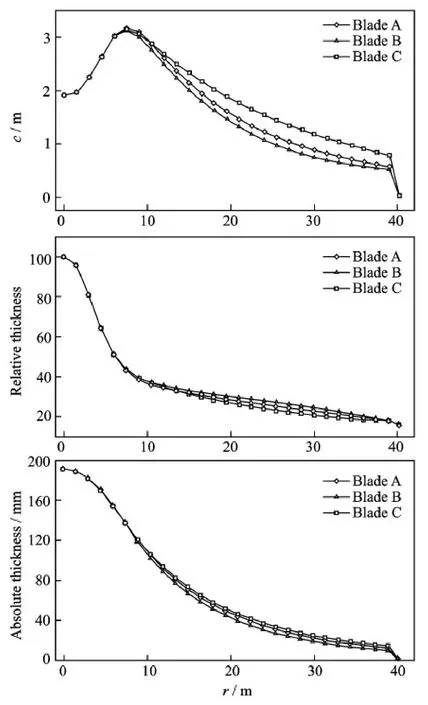
Fig.5　Blade chord and thickness distributions

4　Conclusions

A new vector dominant multi-objective optimization algorithm，referred as VD-MOEA，incorporating basic evolution strategies and vector methods，has been proposed and applied in the field of aerodynamic-structural integrative design of wind turbine blades.A set of virtual vectors，which are used to guide optimal solutions in advancing to the Pareto optimal front with high efficiency，are elaborately constructed in the method.In comparison with the conventional methods，VD-MOEA can obtain a complete optimal solution set of uniform distributions through a single process，and shows the significant advantages in both population diversity preservation and optimization efficiency.The proposed algorithm is then used to design a 1.5 MW wind turbine blade with three conflicting optimization objectives，and a set of optimized blades has be obtained.At least one blade has higher performance，less mass and less root ultimate thrust than the reference Aerodyn-1.5 MW blade without any design inputs changed.VD-MOEA can be used as a general high-performance approach in multi-objective optimization design of wind turbine blade.

Acknowledgements

This work was funded jointly by the National Basic Research Program of China (″973″Program ) (No.2014CB046200)，the National Natural Science Foundation of China (No.51506089)，the Jiangsu Provincial Natural Science Foundation (No.BK20140059)，and the Priority Academic Program Development of Jiangsu Higher Education Institutions.

References:

［1］MAKI K，SBRAGIO R，VLAHOPOULOS N.System design of a wind turbine using a multi-level optimization approach［J］.Renewable Energy，2012，43: 101-110.

［2］MARLER R T，ARORA J S.Survey of multi-objective optimization methods for engineering［J］.Journal of Structural and Multidisciplinary Optimization，2004，26 (6) : 369-395.

［3］KUMAR S P，DEB K.On finding multiple Pareto-optimal solutions using classical and evolutionary generating methods［J］.European Journal of Operational Research，2007，181(3) : 1630-1652.

［4］KUSIAK A，ZHANG Z，LI M.Optimization of wind turbine performance with data-driven models［J］.IEEE Transactions on Sustainable Energy，2010，1 (2) : 66-76.

［5］WANG L，WANG T，LUO Y.Improved non-dominated sorting genetic algorithm (NSGA) -II in multi-objective optimization studies of wind turbine blades［J］.Applied Mathematics and Mechanics，2011，32: 739-748.

［6］WANG L，WANG T，WU J，et al.Multi-objective optimization design of wind turbine blades based on improved NSGA-Ⅱ［J］.Journal of Nanjing University of Aeronautics＆Astronautics，2011，43 (5) : 672-676.(in Chinese)

［7］DAS I，DENNIS J E.Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multi-criteria optimization problems［J］.Siam Journal on Optimization，1998，8(3) : 631-657.

［8］MESSAC A，ISMAIL-YAHAYA A，MATTSON C A.The normalized normal constraint method for generating the Pareto frontier［J］.Structural and Multidisciplinary Optimization，2003，25(2) : 86-98.

［9］Deb K.A fast and elitist multiobjective genetic algorithm: NSGA-II［J］.IEEE Transactions on Evolutionary Computation，2002，6(2) : 182-197.

［10］ZITZLER E，LAUMANNS M，THIELE L.SPEA 2 : Improving the performance of the strength Pareto evolutionary algorithm［R］.Technical Report 103，Computer Engineering and Communication Networks Lab (TIK)，Swiss Federal Institute of Technology (ETH) Zurich，2001.

［11］BROCKHOFF D，ZITZLER E.Improving hypervolumebased multiobjective evolutionary algorithms by using objective reduction methods［C］/ /Evolutionary Computation，2007.CEC 2007.IEEE Congress on.［S.l.］: IEEE，2007: 2086-2093.

Dr.Wang Long received the Ph.D.degree in aerodynamic from Nanjing University of Aeronautics and Astronautics (NUAA) in 2014.He is currently a postdoctor at State Key Laboratory of Mechanics and Control of Mechanical Structures.He is actively pursuing research in wind turbine multi-objective design，aeroelastics and structural vibration analysis.

Dr.Wang Tongguang is the Director of Jiangsu Key Laboratory for Wind Turbine Design at NUAA.He was designated as the Chief Scientist of the″973 Program″by the Ministry of Science and Technology，China in 2007，and successfully completed the project″Fundamental Study of Large Scale Wind Turbine Aerodynamics″.As the Chief Scientist again，he is now in charge of another project of the″973 Program″—″Key Mechanical Issues and Design of Large Scale Wind Turbines″.Prof.Wang graduated from NUAA with B.S.degree and M.S.degree in 1983 and 1988，respectively，and he received his Ph.D.degree from the University of Glasgow in 1999 and has been a postdoctoral fellow at the University of Glasgow from October 1999 to August 2001.During this period，he was invited to join in the Wind Turbine Unsteady Aerodynamics Experiment-Blind Comparison，organized by the National Renewable Energy Laboratory (NREL) of USA.His paper″An examination of key aerodynamic modeling issues raised by the NREL Blind Comparison″was awarded The Best Paper Prize by ASME/AIAA in 2002.

Mr.Wu Jianghai is a Ph.D.candidate of Department of Aerodynamics at College of Aerospace Engineering，NUAA.His research interests include numerical simulation and wind turbine design.

Dr.Ke Shitang is an associated professor at NUAA.He received his Ph.D.degree from Tongji University in 2012.His research interests lie in aeroelastics and structural vibration analysis.

(Executive Editor: Zhang Tong)