基于离散傅里叶变换的过程工业报警泛滥序列聚类分析及应用

陈忠圣，高慧慧，徐圆，朱群雄（北京化工大学信息科学与技术学院，北京 100029）



基于离散傅里叶变换的过程工业报警泛滥序列聚类分析及应用

陈忠圣，高慧慧，徐圆，朱群雄
（北京化工大学信息科学与技术学院，北京 100029）

摘要：报警泛滥是过程工业报警管理中普遍存在且难以解决的问题。报警泛滥序列聚类分析有助于报警根源分析和预警。针对目前报警泛滥序列相似度测量方法存在的缺陷，如对报警序列长度限制、计算复杂、依赖参数，采用基于离散傅里叶变换的方法在频域对报警泛滥序列进行相似性分析，提出了离散傅里叶功率谱的欧氏距离作为度量报警泛滥序列相似度距离的方法，计算不同报警泛滥的相似度距离，再通过非加权组平均法获得报警泛滥序列的聚类树状图，根据相似度距离，确定报警泛滥的模式，帮助操作员确定异常根源，做出快速响应。TE仿真过程在不同干扰下的应用实例验证了该方法的有效性、准确性。

关键词：报警泛滥序列；离散傅里叶变换；相似度；聚类分析

2015-12-16收到初稿，2015-12-30收到修改稿。

联系人：朱群雄。第一作者：陈忠圣（1994—），男，硕士研究生。

引 言

报警系统通常为过程变量设置了4类报警限[1]： HH（高高）、H（高）、L（低）、LL（低低）。当过程变量超过了预先设置报警限，报警产生，报警系统记录相应报警信息，主要包括报警时间（time）、报警变量（tag）、报警类型（alarm type）。由于报警系统的设计缺陷和维护不当，大量的误报警和滋扰报警引发了报警泛滥。报警泛滥的存在，淹没了许多关键报警，过量的报警，远远超出了操作员的处理水平，给操作员的决策和诊断带来困难，严重威胁生产安全。

EEMUA将报警泛滥定义为10 min内操作员遭遇至少10个报警[1-4]。近三十多年的研究成果为报警管理开发了各种方法和工具，但报警泛滥仍然是报警管理中难以解决的问题[3,5]。在基于相似性的技术框架下，异常序列检测关键点是相似性度量[4]。文献[6]采用字符串距离（Levenshtein距离）度量连续报警的相似度，结合动态规划算法，计算编辑距离矩阵，用层次聚类的方法对连续报警聚类，解决了连续报警序列识别的问题，但当报警序列长度较长时，带来较大的时间与计算开销。文献[7]采用基于Sorgenfrei系数和相关性时延分布的方法检测相关报警，通过对时延进行统计分析，实现对关联报警的识别，但计算复杂。文献[8]采用高斯核函数将历史报警数据转换成连续的伪随机时间序列以降低对误报、漏报和抖动报警的影响，用SVD对报警聚类簇进行分解，制定多变量报警策略，但该方法依赖于高斯核函数的方差与伪随机序列的采样率的整定。文献[9]采用带时延的滑动窗口模型计算报警序列的相似度，通过结合报警序列相似度分析与过程数据的因果分析，解决连续报警传播通道的识别问题，但报警序列的相似度依赖于时延的准确估计。基于DFT相似度测量是一种非比对的方法，计算简单、实现方便、不依赖其他参数。目前，大多数序列相似度度量方法只在时域对序列进行相似性分析，而基于DFT相似度测量在频域对序列进行相似性分析，且不受序列长度的影响。与许多非比对相似度测量方法不同，前者在变换前后不丢失序列信息，在序列分类和比较中更加准确[10]。

为了克服已有的报警泛滥序列相似度度量方法计算复杂、依赖参数等缺陷，本文采用基于DFT相似度测量方法挖掘报警泛滥序列簇（模式）。以离散傅里叶功率谱的欧氏距离作为报警泛滥序列相似度距离的度量，计算报警泛滥序列间的距离矩阵，再通过非加权组平均法（unweighted pair group method with arithmetic mean，UPGMA）获得报警泛滥序列的聚类树状图，工作流程可归纳为4个步骤，如图1所示。一个报警泛滥簇（模式）通常相应于一个特定的潜在异常（干扰），报警泛滥簇可通过对历史报警聚类分析获得，报警泛滥簇对应的根本原因，可由专家分析获得。一旦发现当前发生的报警泛滥属于某个报警泛滥簇，操作员可由此确定异常的根本原因，快速做出应对措施。因此，本文的方法在动态报警抑制方面具有潜在的应用前景。

1 基于DFT相似度测量方法描述

1.1 报警泛滥序列的二进制序列表示

报警系统运行过程中，产生大量的报警数据，报警数据以报警日志的形式记录在报警数据库中[11]。设T为报警类型集，T={HH,H,L,LL}，a(a∈T)表示一种报警类型。x(n)表示过程信号序列，xtp,a表示针对报警类型a的报警阈值，报警信号序列与过程信号序列x(n)之间的关系为

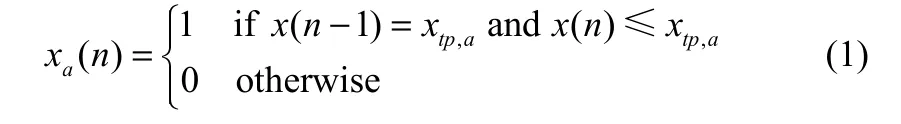
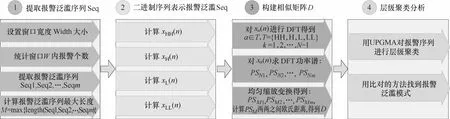
图1 基于离散傅里叶变换的报警序列聚类分析工作流程Fig.1 Work flow chart of discrete Fourier transform-based alarm flood sequence cluster analysis

式中，n表示时间单元，a∈T。报警数据可由式(1)直接转化成多报警的时间序列S。连续报警序列S={s,Ts,Te}，表示处于时间间隔[Ts,Te]的先后报警序列。W={w,ts,te}是序列S上的宽度为Width的时间窗口，且W⊆S，ts＞Ts，te＜Te。给定第i个窗口Wi，起点时刻Ti，终点时刻Tend，窗口宽度Width=Tend−Ti，滑动步长step，报警序列S被分割成一系列等宽度的时间窗口。依据EEMUA制定的基准，若10 min内至少有10个报警产生，则视为报警泛滥。本文设定窗口宽度Width为10 min，统计窗口Wi内的报警个数，若numi≥10，窗口Wi对应的序列Seqj为报警泛滥序列，i≥j，Seqj表示第j个报警泛滥序列。由式(1)，报警泛滥序列Seq(n)可分解为4个子序列，xHH(n)、xH(n)、xL(n)、xLL(n)分别表示报警类型为高高（HH）、高（H）、低（L）、低低（LL）报警泛滥子序列。图2列出了2个报警泛滥序列和相应的4个子序列。

1.2 离散傅里叶变换

图2 用4个二进制序列表示报警泛滥序列Fig.2 Alarm flood sequence representation using 4 binary sequences

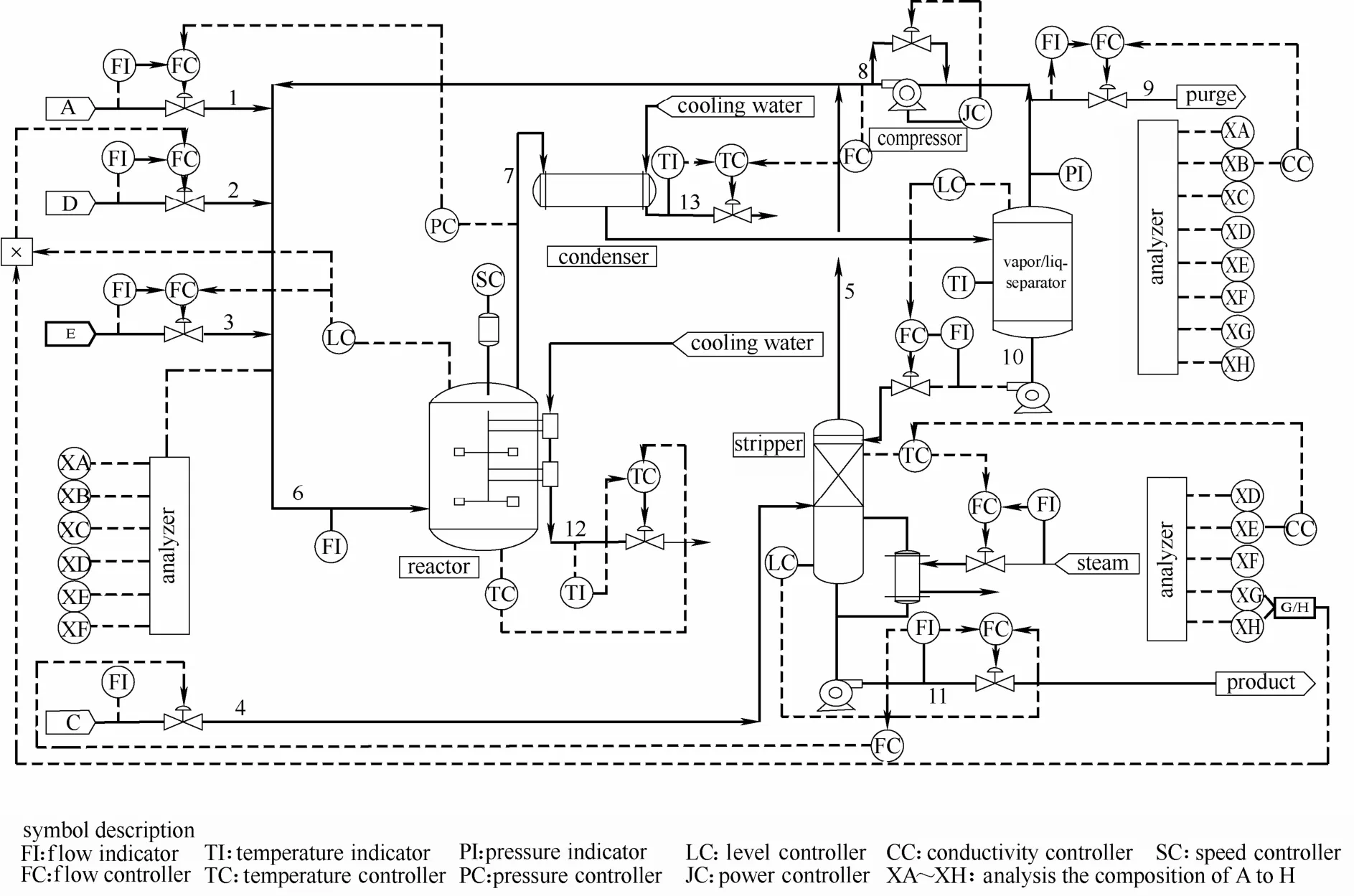
图3 TE过程工艺流程Fig.3 Process flow diagram of Tennessee Eastman process

离散傅里叶变换是数字信号分析的重要工具，它能将时域上有限长信号的采样变换为频域上有限长的采样序列。报警泛滥序列的离散傅里叶变换频谱分析可以检测出原始报警信号潜在的周期信息，识别重复报警，为预警提供信息。时域上长度为N的采样信号序列xa(n)的离散傅里叶变换为

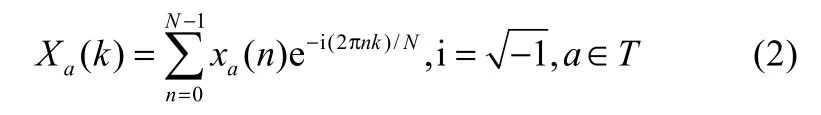
令XHH(k)、XH(k)、XL(k)、XLL(k)分别表示报警子序列xHH(n)、xH(n)、xL(n)、xLL(n)的离散傅里叶变换。定义信号xa在频率k下的离散傅里叶变换功率谱PS(k)为

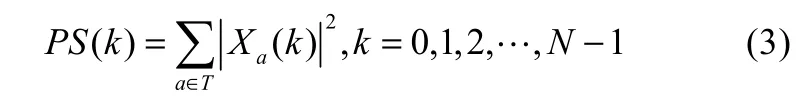
1.3 用DFT功率谱构建报警泛滥序列相似距离矩阵

离散傅里叶变换给出了原始报警序列xa(n)在频域中的唯一表达Xa(k)，Xa(k)包含了完整的xa(n)信息。报警泛滥子序列xa(n)的DFT功率谱PS(k)包含了第k个位置的报警分布信息，因此采用DFT功率谱度量不同报警泛滥序列的相似度。

由DFT功率谱的定义可知，不同长度的报警泛滥序列的DFT功率谱长度不同，所以原始的DFT功率谱不能直接用于度量不同长度报警泛滥序列相似性。采用均匀缩放变换[10]将不同长度的DFT功率谱转化成相同长度的DFT功率谱。该方法将较短序列中一个或两个连续的元素加入原始序列中，从而扩展原始序列。令PSN表示长度为N的原始DFT功率谱，PSM表示长度为M，由原始DFT功率谱PSN均匀缩放变换得到的扩展DFT功率谱，定义原始DFT功率谱PSN到扩展DFT功率谱PSM的均匀缩放变换

图4 不同干扰下报警泛滥序列聚类树状图Fig.4 Dendrograms of alarm flood sequences under different disturbances

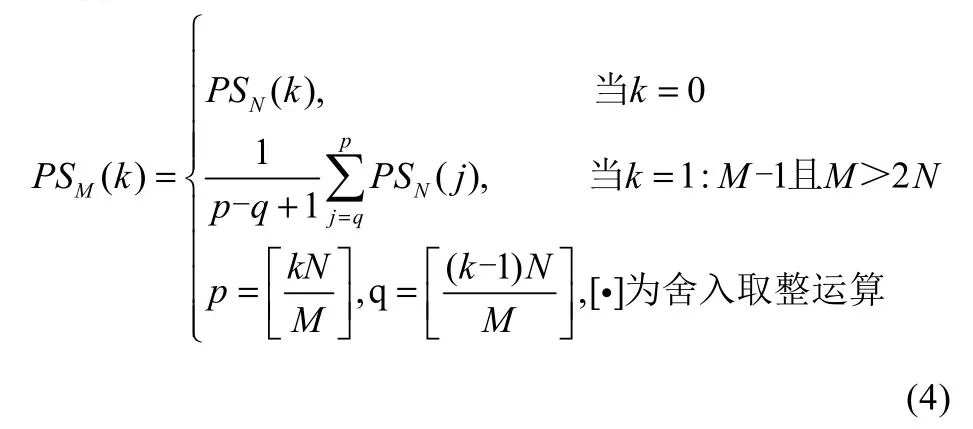
M的大小取决于报警泛滥序列的最大长度。经过均匀缩放后，扩展DFT功率谱可直接用于度量不同长度报警泛滥序列的相似度。一个报警泛滥序列，对应一个M维频域向量PSM，对于m个报警泛滥序列，有m个M维向量PSM1,PSM2,…,PSMm，计算向量PSM两两之间的欧氏距离，归一化后，得到报警泛滥序列相似距离矩阵Dm×m。

D(i,j) ∈[0,1]，D(i,j)越接近1（0），报警泛滥序列Seqi和Seqj越相似（不相似）。

2 实例研究

2.1 TE过程

TE过程[12-14]（Tennessee Eastman process）用于化工过程模拟，是一个真实的化工仿真平台。主要包含5个操作单元：两相反应器、冷凝器、气液分离器、回收压缩机、汽提塔。该过程包括4个不可逆放热反应，4种反应物，生成2种产品（G和H），伴随1种副产品（F）产生，12个操纵变量，41个测量变量，20种过程干扰。工艺流程如图3所示，TE过程部分干扰见表1。

2.2 TE过程用UPGMA获得报警泛滥序列的聚类树状图

图5 报警泛滥序列比对（Seq 558与Seq 560，10个比对）Fig.5 Alarm flood sequences alignment(Seq 558 and Seq 560, number of alignment is equal to 10)

报警泛滥序列聚类分析有助于报警根源分析和预警。通过聚类分析，可以找到不同报警泛滥序列的共同泛滥模式。通常，一个报警泛滥模式对应于一个异常状况，获取泛滥模式意味着找到了引发报警泛滥的根源。同时，通过相似性技术，若发生的报警与匹配池中的候选泛滥模式具有极高的相似性，能预测未来发生的报警情况，实现预警。

表1 TE部分干扰[12]Table 1 Partial disturbances in TE process[12]

UPGMA是一种自下而上的凝聚层次聚类方法，通过比较节点的相似距离，构造聚类树状图。UPGMA工作过程为：首先将相似距离最小的2个节点聚成一簇，生成新的节点，再比较新节点与其他节点的相似距离，把相似距离最小的2个节点聚成一簇，如此反复，直到形成一棵完整的聚类树。

基于DFT相似度测量方法，得到报警泛滥序列相似距离矩阵D，再通过UPGMA进行聚类，获得报警泛滥序列的聚类树状图。

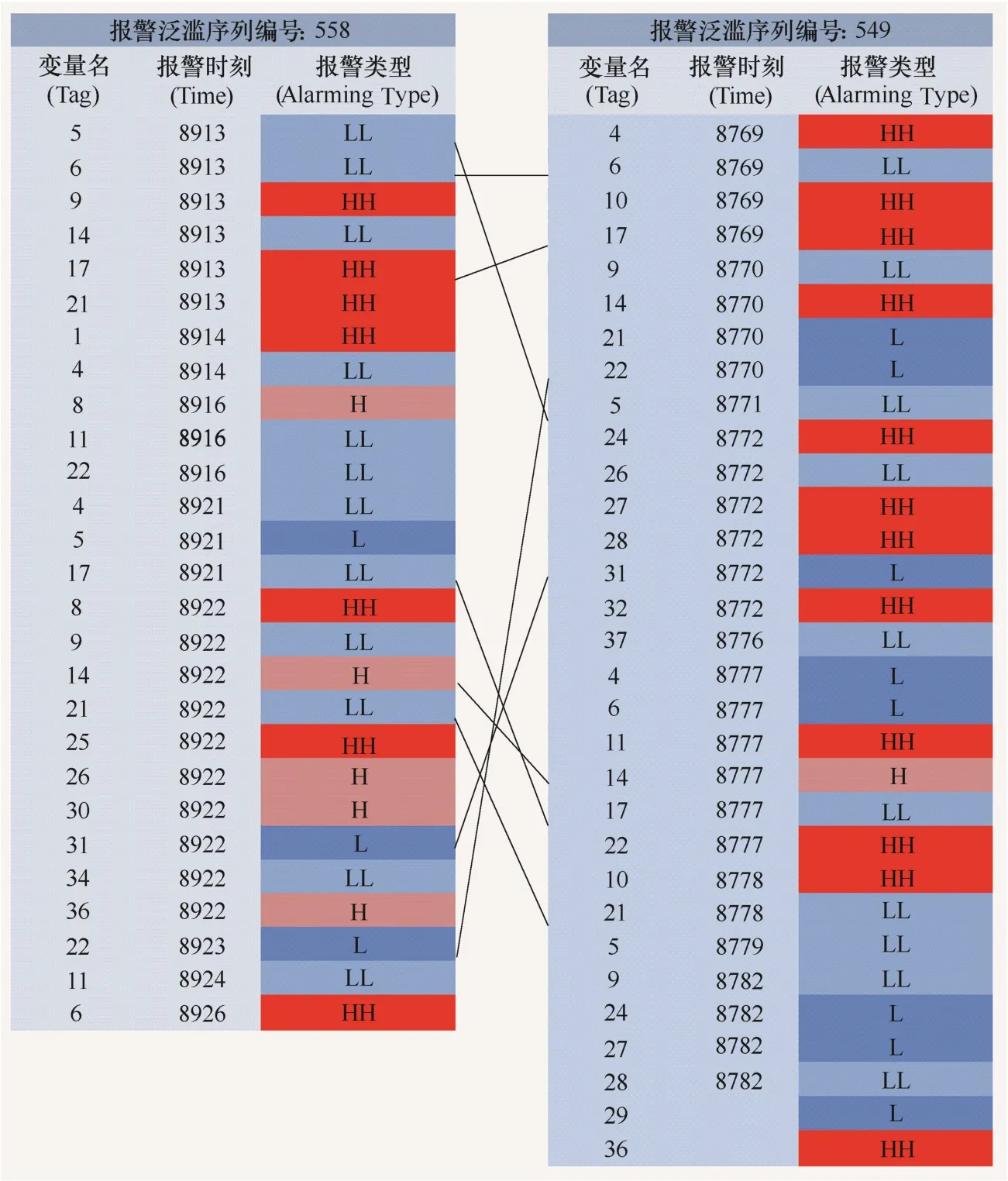
图6 报警泛滥序列比对（Seq 558与Seq 549，8个比对）Fig.6 Alarm flood sequences alignment(Seq 558 and Seq 549, number of alignment is equal to 8)

运行TE过程15 h，将前2 h视作开车阶段。为41个测量变量用3δ法设置H、L报警限，5δ法设置HH、LL报警限。为使系统状态达到充分稳定，让系统运行时间足够长，在开车阶段后，分别施加干扰：IDV 1、IDV 2、IDV 4，共产生3 个12000组历史数据集。IDV 1、IDV 2、IDV 4 是TE过程典型的干扰[14]，相同干扰下产生的报警泛滥序列具有高度的相似性，通过UPGMA获得聚类树状图。

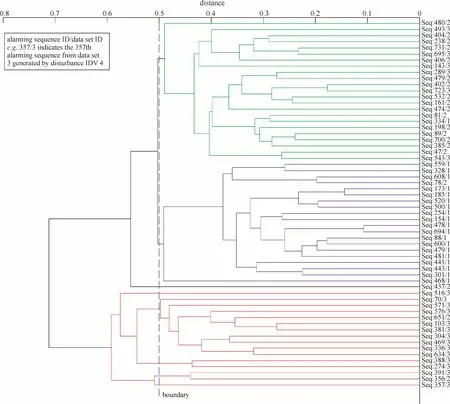
图7 用UPGMA方法获得报警泛滥序列聚类树状图Fig.7 Dendrograms of alarm flood sequences by UPGMA

用基于游程分布定量测量的方法[15]消除抖动报警，合并5 s内出现的相同报警，对3个数据集消除抖动报警后的报警情况如表2所示。

在干扰IDV 1下，时刻145～159和226～235对应的报警泛滥片段如图2所示。通过基于DFT相似度测量方法，在DFT功率谱空间中，计算M维频域向量PSM的欧氏距离，构造相似距离矩阵D，用UPGMA获得干扰IDV 1、IDV 2、IDV 4下报警泛滥序列的相似距离聚类树状图。图4(a)～(c)分别显示了在干扰IDV 1、IDV 2、IDV 4下32次报警泛滥序列的聚类结果。

表2 不同干扰下的报警情况Table 2 Alarming results under different disturbances

相似距离阈值将聚类树状图划分成不同的簇，相似距离阈值是根据聚类结果简单设定的，而不是计算获得的[16]。调整相似距离阈值，在0.5左右时，同一干扰下的报警泛滥序列基本聚为一类。由于同类干扰下，报警泛滥序列相似度高，因此本文用比对的方法验证上述结果的合理性。以图4（c）中报警泛滥序列Seq 558、Seq 560、Seq 549为例，序列Seq 558、Seq 560在聚类树状图中直接邻接，相似性较高，而Seq 558和Seq 549不直接邻接，相似性较低。

由图5和图6，序列Seq 558与Seq 560的比对个数比序列Seq 558与Seq 549的比对个数多。因此序列Seq 560比Seq 549更相似于Seq 558，验证了图4聚类结果的合理性。

为了进一步论证聚类结果的正确性，分别随机选取来自数据集1、2、3各20个报警泛滥序列，用基于DFT相似度测量方法处理后，再用UPGMA聚类，取得良好的聚类效果，如图7所示。

图7中，来自数据集1（在干扰IDV 1下产生）的报警泛滥序列聚集到蓝色一簇，来自数据集2（在干扰IDV 2下产生）的报警泛滥序列聚集到绿色一簇，来自数据集3（在干扰IDV 4下产生）的报警泛滥序列聚集到红色一簇。除356/2等8个序列不能正确聚类外，其余序列均能正确聚类，准确度为86.67%。

图8 用k-means方法的聚类结果Fig.8 Clustering result by k-means method (k=3, silhouette=0.2379)

为了更进一步验证本文提出的基于DFT方法的有效性和UPGMA聚类算法的优越性，采用上述相同数据集，先用基于DFT相似度测量方法计算相似距离矩阵，再用k-means方法进行聚类。多次选取不同的初始中心点k，最后确定k为3。用k-means方法的聚类结果如图8所示，共有11个序列不能正确聚类，准确度为81.67%。

3 结 论

针对传统的报警泛滥序列相似度度量方法计算复杂、依赖参数等缺陷，本文提出了DFT功率谱作为度量报警泛滥序列相似度距离的方法，结合

UPGMA和k-means聚类方法，形成了一种适合解决过程工业报警泛滥的聚类分析方法，解决了报警泛滥模式匹配问题，在一定程度上抑制了报警泛滥现象。该方法计算简单、实现方便、不依赖其他参数。TE仿真过程不同干扰下的应用实例表明，该方法准确、有效。

References

[1] ZHU J F, SU Y D, ZHAO J S, et al. A dynamic alarm management strategy for chemical process transitions [J]. Journal of Loss Prevention in the Process Industries, 2013, 30: 1-12.

[2] EEMUA. Alarm Systems: A Guide to Design, Management and Procurement[M]. 2nd ed. London: Engineering Equipment and Materials Users’ Association, 2007.

[3] JASON C L, PETER B ,MISCHA T, et al. Addressing alarm flood situations in the process industries through alarm summary display design and alarm response strategy [J]. International Journal of Industrial Ergonomics, 2014, 44: 395-406.

[4] CHENG Y, IZADI I, CHEN T W. Pattern matching of alarm flood sequences by a modified Smith–Waterman algorithm [J]. Chemical Engineering Research and Design, 2013, 91: 1085-1094.

[5] ZHU Q X, GAO H H, LIU F F, et al. Research process of alarm system in process industries [J]. Computers and Applied Chemistry, 2014, 31(2): 129-134.

[6] AKATSUKA S, NODA M. Similarity analysis of sequential alarms in plant operation data by using levenshtein distance[C]// PSE ASIA, Proc. 6th International Conference on Process Systems Engineering. Kuala: PSE ASIA Press, 2013: 129-134.

[7] YANG Z J, WANG J D, CHEN T W. Detection of correlated alarms based on similarity coefficients of binary data [J]. IEEE Transactions on Automation Science and Engineering, 2013, 10(4): 1014-1025.

[8] YANG F, SHAH S L, XIAO D Y, et al. Improved correlation analysis and visualization of industrial alarm data [J].ISA Transactions, 2012, 51: 499-506.

[9] WANG J, LI H G, HUANG, J W, et al. A data similarity based analysis to consequential alarms of industrial processes [J]. Journal of Loss Prevention in the Process Industries, 2015, 35: 29-34.

[10] YIN C C, CHEN Y, STEPHEN S T Y. A measure of DNA sequence similarity by Fourier transform with applications on hierarchical clustering [J]. Journal of Theoretical Biology, 2014, 359: 18-28.

[11] DANEELS A, SALTER W. What is scada?[C]//Trieste, InternationalConference on Accelerator and Large Experimental Physics Control Systems: Italy, Conf.Proc., 1999:339-343.

[12] DOWNS J J, VOGEL E F. A plant-wide industry process control problem [J]. Computers Chem. Engng., 1993, 17(3):245-255.

[13] LYMAN P R, GEORGAKIS C. Plant-wide control of the Tennessee Eastman process [J].Computers Chem. Eng., 1995, 19(3): 321-331.

[14] KANADIBHOTLA R S, RIGGS J B. Nonlinear model based control of a recycle reactor process [J]. Computers Chem. Engng., 1995, 19(8): 933-948.

[15] NAGHOOSI E, IZADI I, CHEN T W. Estimation of alarm chattering [J]. Journal of Process Control, 2011, 21: 1243-1249.

[16] NISHIGUCHI J, TAKAI T. IPL2 and 3 performance improvement method for process safety using event correlation analysis [J]. Computers and Chemical Engineering, 2010, 34: 2007-2013.

研究论文

Received date: 2015-12-16.

Foundation item: supported by the National Natural Science Foundation of China (61473026).

Discrete Fourier transform-based alarm flood sequence cluster analysis and applications in process industry

CHEN Zhongsheng, GAO Huihui, XU Yuan, ZHU Qunxiong
（College of Information Science & Technology, Beijing University of Chemical Technology, Beijing 100029, China）

Abstract：Alarm floods is a prevalent and difficult problem in alarm management of process industry. Alarm cluster analysis is helpful for alarm root cause analysis and alarm prediction. Aiming at the deficiencies of the current similarity measurement methods for alarm flood sequences, such as limitation of length of alarm sequences, computational complexity, depending on parameters, the discrete Fourier transform (DFT)-based method is employed to analysis on similarity among alarm flood sequences in the frequency domain. The Euclidean distance of the DFT power spectra of alarm flood sequences is proposed as a similarity distance metric for alarm floods, similarity distances of different alarm floods are evaluated. Dendrograms of alarm flood sequences by Unweighted Pair Group Method with Arithmetic mean (UPGMA) is obtained, according to similarity distance, determine the pattern of alarm floods and help operators identify the root cause of the abnormal for a rapid response. An application case of TE simulation process under different disturbances demonstrates validation and accuracy of the proposed method.

Key words：alarm flood sequence; discrete Fourier transform; similarity; cluster analysis

DOI：10.11949/j.issn.0438-1157.20151912

中图分类号：TP 277; TQ 086; TE 687

文献标志码：A

文章编号：0438—1157（2016）03—0788—09

基金项目：国家自然科学基金项目（61473026）。

Corresponding author:Prof. ZHU Qunxiong, zhuqx@buct.edu.cn