分布曲线对象的无偏模型预测控制算法
2016-05-11康岳群徐祖华赵均邵之江浙江大学控制科学与工程学院工业控制技术国家重点实验室浙江杭州310027
康岳群,徐祖华,赵均,邵之江(浙江大学控制科学与工程学院,工业控制技术国家重点实验室,浙江 杭州 310027)
分布曲线对象的无偏模型预测控制算法
康岳群,徐祖华,赵均,邵之江
(浙江大学控制科学与工程学院,工业控制技术国家重点实验室,浙江 杭州 310027)
摘要:随着系统总体性能要求的提高,分布曲线对象的控制问题成为研究热点。分布曲线对象是通过宏观的操作手段控制微观的输出曲线,不是任意形状的目标曲线都是能无偏跟踪的。提出了一种分布曲线对象的无偏模型预测控制算法。该方法首先采用B样条模型进行分布曲线对象的描述,其次通过复合梯形方法对滚动优化命题进行离散化,最后采用二次规划方法进行无偏目标曲线计算,以实现无偏控制。仿真结果表明了算法的有效性。
关键词:分布曲线对象;模型预测控制;无偏控制;优化;数学模拟
2015-12-22收到初稿,2015-12-29收到修改稿。
联系人:徐祖华。第一作者:康岳群(1991-),男,硕士研究生。
引 言
在传统的工业控制中,被控变量通常是n维空间中的的一个点。随着控制系统性能要求的提高,面临着曲线控制的需求,被控变量从n维空间的一个点过渡到n维空间中的一条曲线。例如对于聚合产品而言,高分子链和低分子链代表了不同的特性,在传统工业过程控制中常采用平均分子量或者熔融指数等宏观指标作为被控目标[1-3],但是这些宏观指标无法反映出完整的分子结构,导致聚合产品性能如抗冲击性能、热力学性能等达不到预期的要求。因此为了满足性能要求,提出对于反映完整分子结构信息的分子量分布曲线的控制是十分必要的。分布曲线的控制不仅仅用于聚合反应的分子量分布,还广泛用于其他化工领域,如造纸过程纸张两维质量分布控制、燃烧过程温度场分布控制等等。
分布曲线的控制在近十多年来得到了广泛的关注,Wang[4]利用神经网络建立随机分布模型,对静态系统和动态系统的建模和控制都进行了研究,随后为这种新型随机系统设计鲁棒控制[5],自适应控制和非线性控制算法[6],解决了随机系统的建模与控制问题,并且将所推导的控制算法成功运用在造纸的生产过程中。张春雨[7]利用B样条神经网络和线性递归神经网络相结合的方法对管式聚合反应的温度分布进行了建模,在此基础上引入了实时模型误差的策略,提出了扩展的积分平方误差控制指标,解决了管式聚合反应的温度分布控制问题。吴海燕[8]提出当分子量分布曲线采用离散正交多项式来描述时,权值和分子量分布的矩向量存在线性关系,并利用最优算法实现了分子量分布的形状控制。申珊华等[9]基于灰箱模型对分子量分布矩值设计预测控制器,利用分子量分布矩值可测的功能完成反馈校正的功能。
分布曲线对象是通过宏观的操作手段控制微观的输出曲线,不是任意形状的目标曲线都是能无偏跟踪的。在现有研究成果中,无偏控制问题仍然没有很好地解决。模型预测控制由于其模型预测、滚动优化、反馈校正的鲜明特点,使其成为目前公认处理复杂过程约束控制的有效算法,在石油、化工等过程领域中得到成功应用[10-13]。因此,本文在模型预测控制框架下进行分布曲线对象的无偏控制研究,首先采用B样条模型进行分布曲线对象的描述,其次通过复合梯形方法对滚动优化命题进行离散化,最后通过二次规划方法进行无偏目标曲线计算,以实现无偏控制。
1 分布曲线对象模型
本文采用如下模型进行分布曲线描述
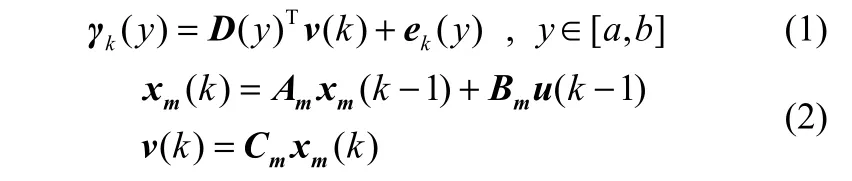
其中,v(k)=[v1(k),v2(k),…,vnv(k)]T为nv维权值向量,D(y)=[D1(y),D2(y),…,Dnv(y)]T为nv维B样条基函数向量,xm(k)为nx维状态向量,u(k)为nu维输入向量,e(y)是不可测输出扰动。
令Δxm(k)=xm(k)−xm(k−1),η(k)=v(k),Δu(k)=u(k)−u(k−1),则式(2) 转化为如下增量表示形式

令x(k)=[Δxm(k)Tη(k)T]T,则分布曲线对象模型可以用如下方程表示

2 面向分布曲线的模型预测控制
2.1 预测模型
令k时刻已经得到状态的估计值x(k|k),因此,在M个连续的控制增量作用下,系统在未来P个时刻的权值预测如下所示
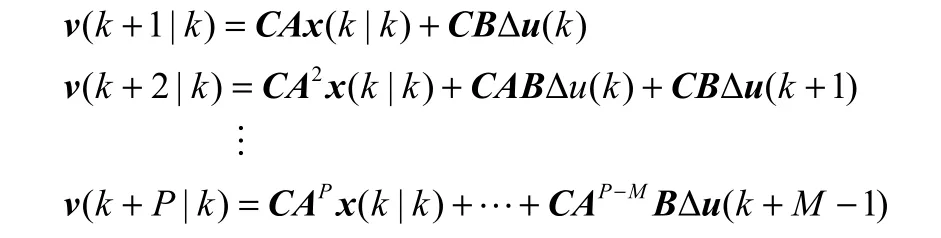
将上述推导整理成如下的预测方程

其中,各变量定义为

通过预测方程式(5)可以对未来P个时刻的曲线形状进行预测控制。
2.2 滚动优化
在采样时刻k,通过最小化性能指标函数(7)确定最优控制序列,使得未来预测输出曲线尽可能接近期望的目标曲线,同时对控制作用的大小加以约束,避免控制作用变化过于剧烈
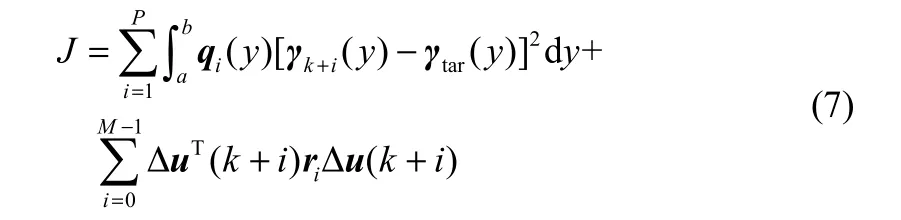
其中,γtar(y)为期望的目标曲线,γk+i(y)为k+i时刻的预测输出曲线,qi(y)为k+i时刻输出误差加权函数,ri为k+i时刻控制增量加权系数,a和b分别为曲线的积分下限和积分上限。采用复合梯形方法对式(7)进行积分离散化,把区间[a,b]进行n等分,步长h=(b−a)/n,得到如下离散化公式
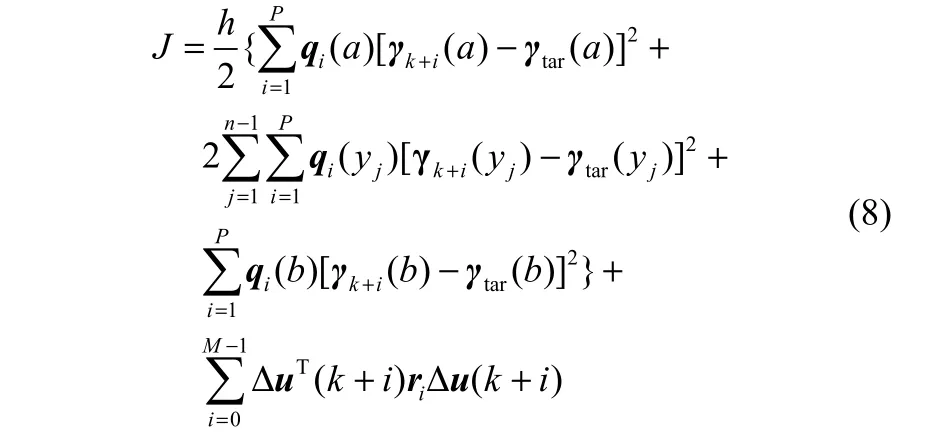
将预测方程式(6)代入上述优化目标,得到性能指标函数
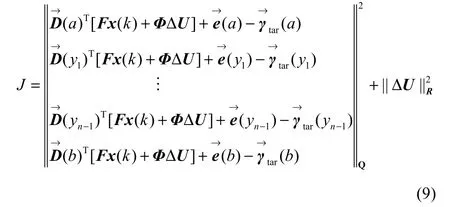
其中,Q和R均为加权矩阵,每一个对角阵Q(yj)对角线上的第i元素表示对未来的第i个时刻分布曲线上yj这一点的重视程度。rij表示对于第i个控制变量在未来的j时刻变化幅度的限制。
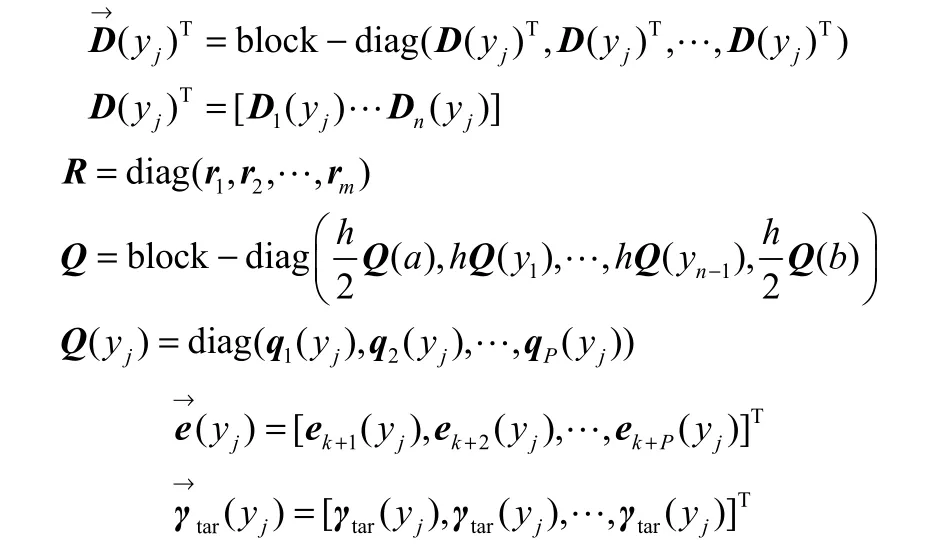
在不考虑输入输出约束的条件下,由极值必要条件∂J/∂ΔU=0求得如下最优解
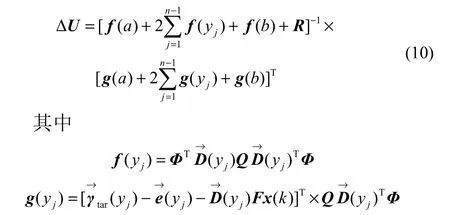
通过式(10)可以求解出未来M个时刻的控制增量,为了防止模型失配出现的偏差,每次只执行第一个控制增量,到了下一个采样时间点继续进行优化计算。
2.3 反馈校正
由于模型失配、不可测干扰等因素存在,系统的实际运行可能偏离理想的优化结果,反馈校正策略必不可少,具体步骤如下。
(1)根据检测仪表,得到分布曲线对象在[a,b]上的若干测量值,通过三次样条插值方法,得到真实分布曲线γk(y)。
(2)通过真实分布曲线γk(y)与预测输出曲线γk|k−1(y),得到预测误差曲线ek(y)。
(3)根据误差曲线ek(y)计算所有的误差向量,代入式(10)计算下一时刻的控制增量。
上述3步组成一次完整的校正,消除由于模型误差以及不可测扰动所带来的影响,使系统的实际运行尽可能逼近理想的优化结果。
3 无偏目标曲线计算
以宏观的控制变量控制微观的分布曲线,由于对象特性本身的原因,不是任意形状的目标曲线都是可达的,特别是在执行机构有约束的情况下。比如对于分子量分布而言,进料的流量、速率都是限定在一个范围之内,低分子比例与高分子比例不能任意变化。因此,有必要在控制分布曲线时根据对象特性对目标曲线进行分析,对不可达的目标曲线做出调整,放弃部分性能要求,以实现无偏控制。
对于分布曲线对象,由式(3)通过推导可以得到分布曲线的稳态模型

其中,vss是稳态权值,γss(y)为稳态分布曲线。在此基础上,通过如下的积分误差优化命题,可以判断出目标分布曲线是否可达。

其中,qss(y)是加权函数,通常重要的微观质量部分权值设置较大,次要的微观质量部分权值设置较小。为了求解上述积分优化问题,采用复合梯形公式进行离散化。因此,可将目标函数J划分成常数项,一次项和二次项之和。
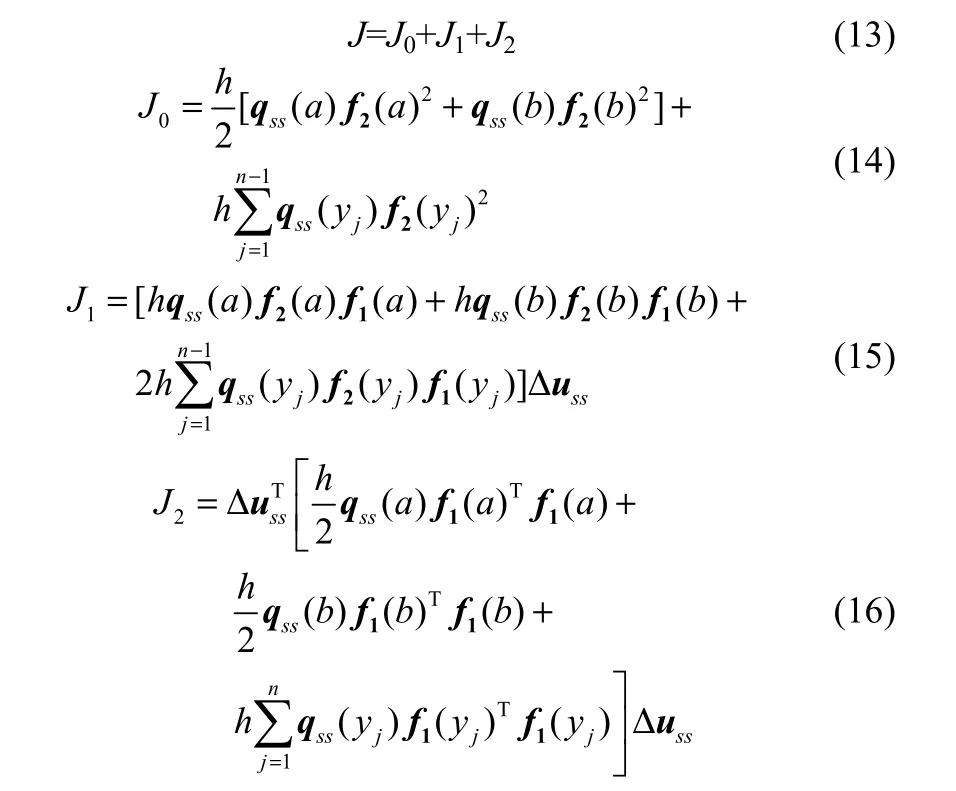
其中,
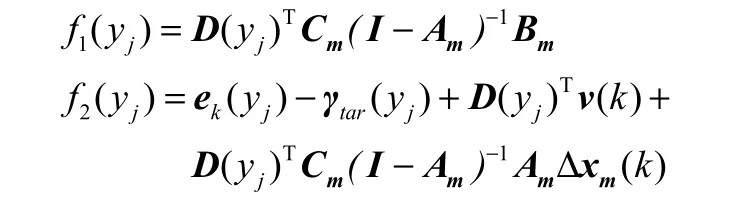
从而转化为标准二次规划命题进行求解。如果稳态误差J*小于误差容限ε,表示目标曲线是可达的;如果稳态误差J*大于误差容限ε,表示目标曲线是不可达的,则通过如下计算公式,计算出一条可达的目标曲线来进行无偏控制。
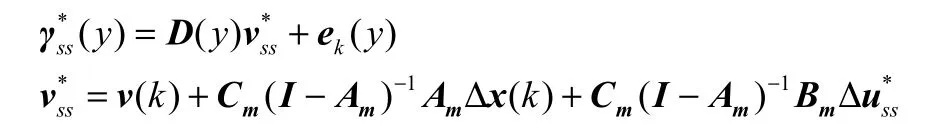
综上所述,分布曲线对象的无偏模型预测控制算法步骤如图1所示。
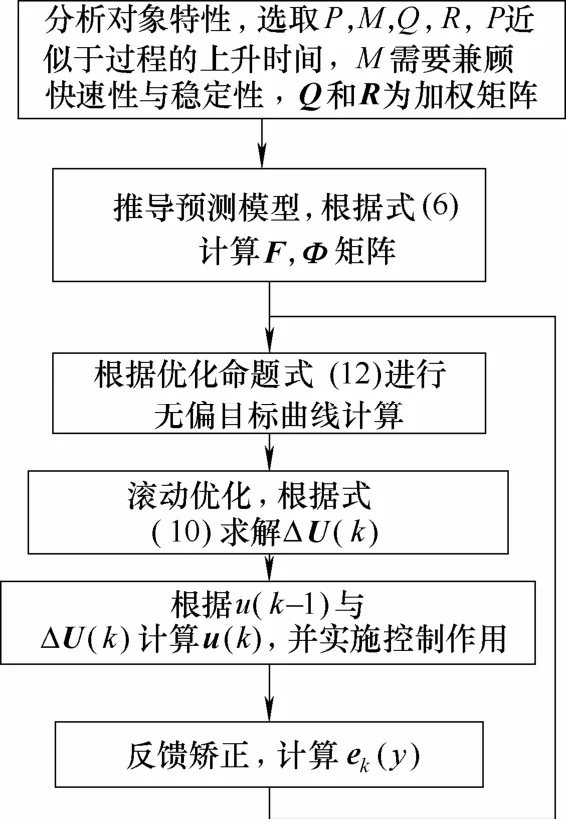
图1 无偏控制实施步骤Fig.1 Flow chart of offset-free control
4 仿真结果
本文针对如下的分布曲线对象设计控制器
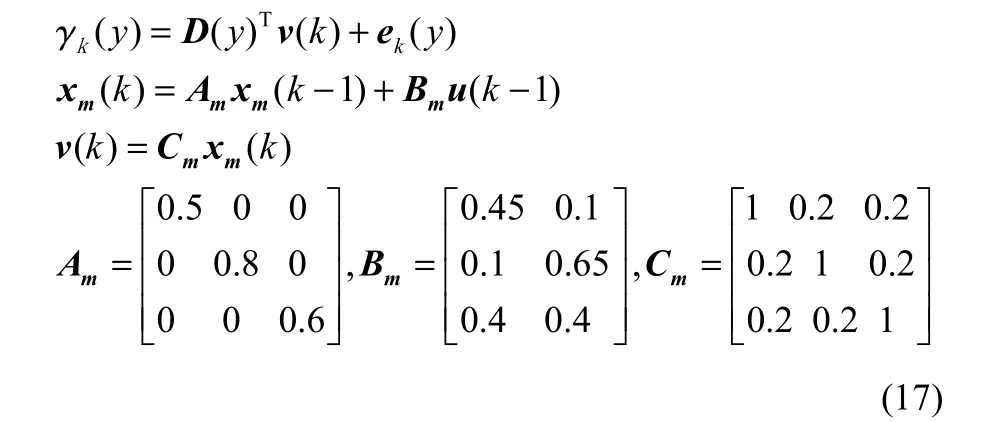
其中,D(y)为3阶B样条基函数,按照如下递推公式[14]
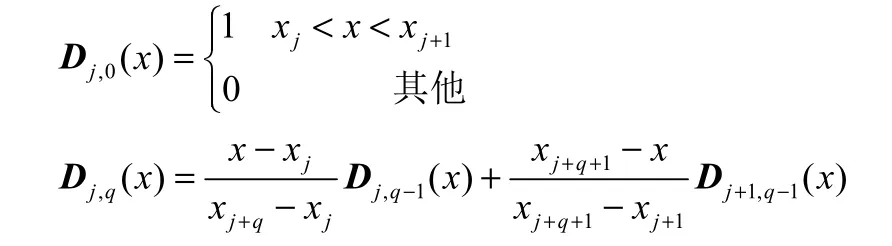
其中,x表示变量,q表示B样条基函数的阶次,j表示第j个基函数。
通常在预测控制中,优化时域P,一般取近似于过程的上升时间,本文选择P=6。控制时域M的选择应当兼顾快速性和稳定性,本文选择M=3。输出偏差加权阵Q的大小反映了每个时刻对预测输出曲线逼近给定曲线的重视程度,控制增量加权阵R是防止控制增量的剧烈变化,为了简单起见这里Q 和R均选取单位阵。
4.1 仿真一
在本次仿真中,对象无模型失配,且目标曲线为
γtar(y)=1.16D1(y)+0.31D2(y)+1.08D3(y) (18)
通过本文提出的无偏目标曲线计算方法,该目标曲线是可达的,稳态误差较小。仿真结果如图2所示,经过10个控制周期,输出曲线已经跟踪上目标曲线。

图2 仿真一控制效果图Fig.2 Closed-loop response of MPC(simulation 1)
4.2 仿真二
在本次仿真中,对象无模型失配,且目标曲线为

通过本文提出的无偏目标曲线计算方法,该目标曲线是不可达的,稳态误差较大。选取qss(y)常值函数,计算出稳态误差最小的可达目标曲线,如图3虚线所示。
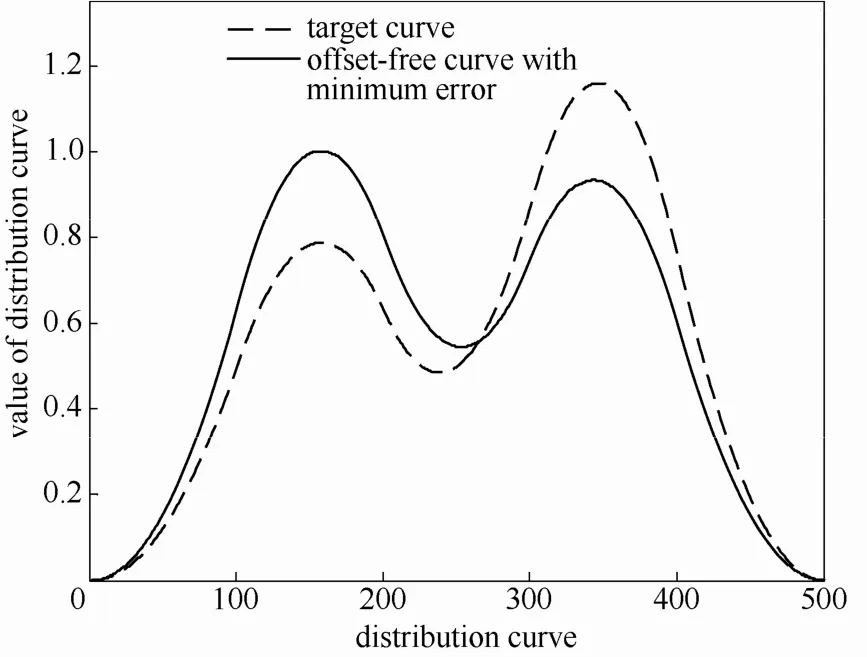
图3 目标形状的无偏性分析Fig.3 Offset-free analysis of target curve
对于新给定的目标曲线,控制效果如图4所示。
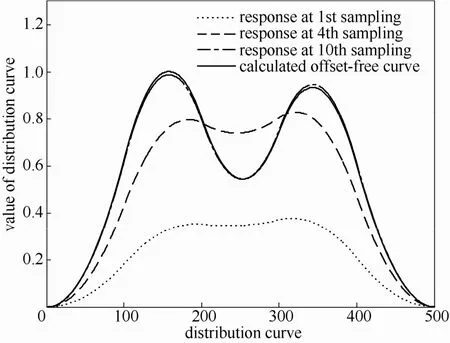
图4 仿真二控制效果图Fig.4 Closed-loop response of MPC(simulation 2)
由仿真结果可知,输出分布曲线经过10个控制周期达到了新的目标曲线,为了区分不同区间的重要性,可以修改稳态误差的权值函数qss(y)。
4.3 仿真三
在本次仿真中,对象存在模型失配,目标曲线可达,在模型存在误差的情况下需要使用反馈校正逼近理想的优化效果。在本例中模型失配是由于模型的基函数数目少于真实对象的数目,导致动态特性与静态特性都存在失配。

基函数如图5所示。

图5 模型失配Fig.5 Model-plant mismatch
从如下仿真结果(图6)中看出,反馈矫正可以针对模型失配进行矫正,到达理想的优化效果。

图6 模型失配控制效果图Fig.6 Closed-loop response of MPC with model-plant mismatch
5 结 论
本文首先采用B样条基函数的描述方式,将曲线控制的动态过程用状态空间来描述,其次利用模型设计预测控制器,使得输出曲线尽可能逼近目标曲线,最后为了分析目标曲线的可达性,推导出模型的稳态表达式,利用二次规划进行求解,解决了分布曲线控制的无偏性问题,下一步工作是针对变形过程开展多分辨率控制。
符 号 说 明
A,B,C——分别为增量模型的系统矩阵、输入矩阵和输出矩阵
D(y) ——B样条基函数向量
M ——预测控制控制时域
P ——预测控制优化时域Q ——误差加权矩阵
R ——控制增量加权矩阵
v(k) ——B样条基函数对应的权值向量
References
[1] 费正顺, 胡斌, 叶鲁彬, 等. 带路径约束的聚烯烃牌号切换操作优化方法 [J]. 化工学报, 2010, 61(4): 893-900.
FEI Z S, HU B, YE L B, et al. Optimal grade transition of polymerization process with path constraints [J]. CIESC Journal, 2010, 61(4): 893-900.
[2] 张伟杰, 梁军, 费正顺, 等. 具有不确定性的聚烯烃牌号切换过程动态优化 [J]. 化工学报, 2011, 62(10): 2797-2804. DOI: 10.3969/ j.issn. 0438-1157.2011.10.018.
ZHANG W J, LIANG J, FEI Z S, et al. Optimal grade transition in polymerization processes under uncertainty [J]. CIESC Journal, 2011, 62(10): 2797-2804. DOI: 10.3969/j.issn.0438-1157. 2011.10.018.
[3] 王平. 淤浆法聚乙烯生产中牌号切换策略研究[D]. 杭州: 浙江大学, 2006.
WANG P. Optimal strategy of grade transition in industrial slurry high-density polyethylene production process[D].Hangzhou: Zhejiang University, 2006.
[4] WANG H. Bounded Dynamic Stochastic Distributions Modeling and Control [M]. London: Springer-Ver-lag Ltd. 2000: 14-20.
[5] WANG H. Robust control of the output probability density functions for dynamic stochastic systems [C]//Proc. of the 1998 Conference on Decision and Control. Tampa, Madison: Omini, 1998: 134-150.
[6] WANG H. Control of the output probability density functions for a class of nonlinear stochastic systems [C]//Proc. of the IFAC Workshop on Algorithms and Architectures for Realtime Control. Cancun, Mexico: Elesvier, 1998: 152-180.
[7] 张春雨. 管式聚合反应温度分布建模及控制方法的研究[D]. 北京:北京化工大学, 2005.
ZHANG C Y. The study of temperature distribution model and control in tubular polymeiuzation reaction[D].Beijing: Beijing University of Chemical Technology, 2005.
[8] 吴海燕. 利用神经网络实现聚合反应分子量分布的建模与控制[D]. 北京: 北京化工大学, 2004.
WU H Y. Modeling and controlling molecular weight distribution for polymerization processes via neural networks[D]. Beijing: Beijing University of Chemical Technology, 2004.
[9] 申珊华, 曹柳林, 王晶.基于分布函数矩的聚合物分子量分布预测控制 [J]. 化工学报, 2013, 64(12): 4379-4384, DOI: 10.3969/j.issn.0438-1157.2013.12. 016.
SHEN S H, CAO L L, WANG J. Predictive control of molecular weight distribution in polymerization reaction based on moment of MWD [J]. CIESC Journal, 2013, 64(12): 4379-4384, DOI: 10.3969/j.issn. 0438-1157.2013.12.016.
[10] 钱积新, 赵均, 徐祖华.预测控制[M].北京: 化学工业出版社, 2007.
QIAN J X, ZHAO J, XU Z H.Model Predictive Control[M]. Beijing: Chemical Industry Press, 2007.
[11] 韩恺, 赵均, ZHU Yucai, 等.一种扰动自适应的鲁棒预测控制算法[J]. 化工学报, 2009, 60(7): 1730-1738.
HAN K, ZHAO J, ZHU Y C, et al.A robust MPC technique with adaptive disturbance model [J]. CIESC Journal, 2009, 60(7): 1730-1738.
[12] 徐祖华, 赵均, 钱积新.基于Min-Max的预测控制鲁棒参数设计[J]. 化工学报, 2004, 55(4): 613-617. XU Z H, ZHAO J , QIAN J X.Robust design method of predictive
controller parameter based on Min-Max ruler [J]. Chinese Journal of Chemical Industry and Engineering(China), 2004, 55(4): 613-617.
[13] 徐祖华, ZHU Yucai, 赵均, 等.新一代的自适应模型预测控制器[J]. 化工学报, 2008, 59(5): 1207-1215.
XU Z H, ZHU Y C, ZHAO J, et al. Next-generation adaptive MPC controller [J]. Chinese Journal of Chemical Industry and Engineering (China), 2008, 59(5): 1207-1215.
[14] 程正兴, 李水根. 数值逼近与常微分方程数值解[M]. 西安: 西安交通大学出版社, 1998.
CHEN Z X, LI S G.Numerical Approximation and Numerical Solution of Ordinary Differential Equations[M]. Xi'an: Xi'an Jiaotong University Press, 1998.
研究论文
Received date: 2015-12-22.
Foundation item: supported by the National High Technology Research and Development Program of China(2014AA041802) and the National Natural Science Foundation of China(U1509209,61273145,61273146).
Offset-free model-predictive control algorithm of distribution process
KANG Yuequn, XU Zuhua, ZHAO Jun, SHAO Zhijiang
(State Key Laboratory of Industrial Control Technology, College of Control Science and Engineering, Zhejiang University, Hangzhou 310027, Zhejiang, China)
Abstract:With the improvement of overall system performance requirements, control problems in distribution process has already become the current research focus. The output of the object of microscopic distribution process are controlled by macro way, not can arbitrary shaped curves track with offset-free. This paper propose an offset-free model predictive control algorithm of controlling the distribution process. First, the method describe the distribution process with B-splines. Second, using composite trapezoidal rule for discretizing proposition of rolling optimization. Finally, using the quadratic programming method to calculate the offset-free target to achieve offset-free control. It proved well performed at simulation experiment.
Key words:distribution process; model-predictive control; offset-free control; optimization; mathematical modeling
DOI:10.11949/j.issn.0438-1157.20151946
中图分类号:TP 13
文献标志码:A
文章编号:0438—1157(2016)03—0701—06
基金项目:国家高技术研究发展计划项目(2014AA041802);国家自然科学基金项目(U1509209, 61273145, 61273146)。
Corresponding author:Prof. XU Zuhua, xuzh@iipc.zju.edu.cn
