具有指数型发生率的离散SIS模型的动力学研究
2016-05-10毛红艳蔺小林
毛红艳, 曹 慧, 蔺小林
(陕西科技大学 文理学院, 陕西 西安 710021)
具有指数型发生率的离散SIS模型的动力学研究
毛红艳, 曹 慧, 蔺小林
(陕西科技大学 文理学院, 陕西 西安 710021)
研究了一类具有指数发生率的离散SIS传染病模型的动力学性态.利用再生矩阵的方法定义了模型的基本再生数;对模型进行分析得到平衡点的存在性和稳定性,同时也得到了模型的持久性;通过参数赋值,利用数值模拟方法对平衡解的相关结果进行了验证.
SIS模型; 差分方程; 平衡点; 渐近稳定性
0 引言
近些年来,传染病模型已经成为生物数学研究的一个热门话题.传染病的发展过程与时间紧密相关,从统计学的观点来看,使用离散时间替代连续时间(采集数据是在离散的时间段收集的)更符合客观实际,特别对具有较慢传播率的传染病更是如此.
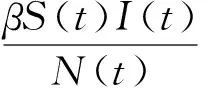
1 SIS模型建立及分析
本文讨论治愈后还会再次感染的传染病模型,即离散SIS传染病模型.离散SIS传染病模型是在仓室模型[3]的基础上,把总人口分为易感者和感染者两个仓室,记t时刻易感者的人口数量为S(t),感染者人口数量为I(t),总人口数量为N(t),满足N(t)=S(t)+I(t).
本文在研究疾病传播过程中,做三个假设:
(1)易感者患病不存在潜伏期,也就是疾病的潜伏期比较短可以忽略不计;
(2)一个染病者一旦与易感者接触就必然具有一定的感染力;
(3)每一个新入人口都是易感者,包括新生儿和迁入人口,且新入人口记为常数Λ.
当单位时间内易感者个体成为感染者概率是1-G(I),其中G:[0,∞]→[0,1]是一个单调函数[4],满足:
G(0)=1,G′(x)<0,G″(x)≥0,∀x∈[0,∞]

图1 SIS模型
运用差分方程[5]表示此模型,则相应的数学模型为:
(1)
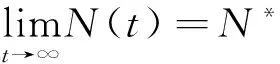

Ω={(S,I)|S≥0,I≥0,S+I≤N*}

下面将在条件S(t)+I(t)≤N*下,研究与模型(1)的极限状态模型(2)解的性态.
(2)
为了下面讨论方便起见,先给出离散线性系稳定性判据.
对线性系统
X(t+1)=AX(t)
(*)
其零解的渐近稳定性有如下判据.
引理2[6](Jury判据)设系统(*)的特征多项式为
Pn(λ)=|λI-A|=a0λ″+a1λn-1+…+an-1λ+an
则系统(*)的零解渐近稳定的充分必要条件为

m=2,3,…,n-1;i=0,1,…,m.
2 基本再生数
基本再生数[7]表示在发病初期,当所有人均为易感者时,一个染病者在其平均染病期内所传染的人数.R0=1往往是系统的一个阈值,通常可用R0讨论传染病的性态.当R0<1时,疾病会最终消失,当R0>1时,疾病会在人群中持续存在.当R0>1且比较大时,表示该传染病很难控制,并可能在该地区爆发大规模的流行病.
对模型(1),根据再生矩阵[8]的方法,可写出矩阵生育矩阵F和过渡矩阵V,其中
V=[p(1-γ)I(t)]
根据基本再生数的计算方法可知:

因此

运用参考文献[9]中的迭代方法,使用数学软件matlab进行数值模拟,可以得到感染者I(t)与三个参数p,β,γ的关系.给定初值,I(0)=25,S(0)=75在满足0
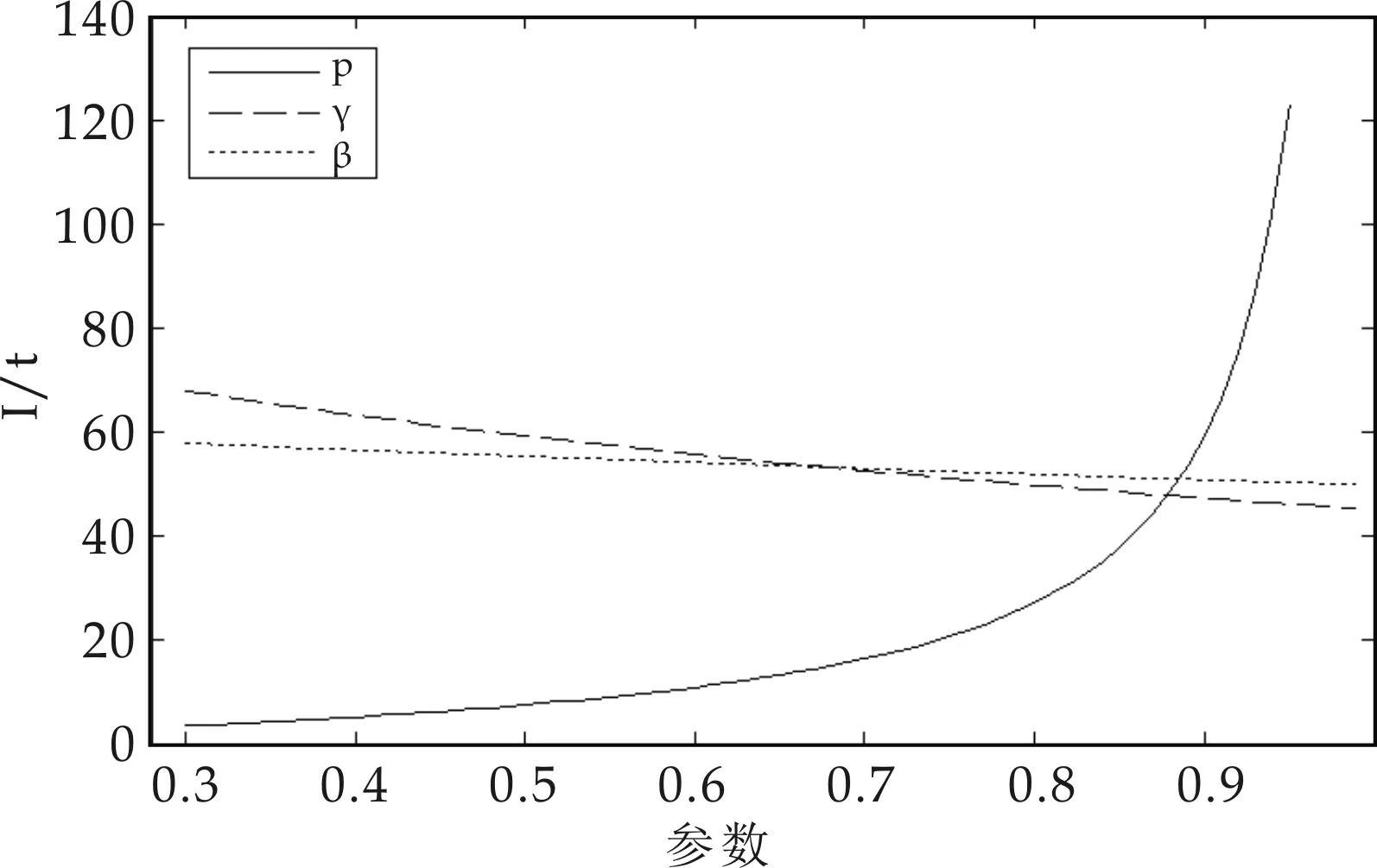
图2 感染者I(t)随三个参数变化趋势图
3 平衡点的存在性和稳定性
证明:首先讨论模型(2)的无病平衡点的存在性.

当p(1-γ+β)>1时,讨论地方病平衡点的存在性,分析模型(2),取f:[0,1]→[0,1],则
f(y)=p(1-e-βy)(1-y)+p(1-γ)y
(3)

f′(y)=pe-βy(β(1-y)+1)-pγ
(4)
f″(y)=-pβe-βy(β(1-y)+2)
(5)



(6)
代入p0
其特征多项式为:
|λI-J0|=(λ-p)(λ-p(1+β-γ)),
可得J0的特征多项式的根为λ1=p,λ2=p(1+β-γ),利用Jury判据可以知道,当p(1-γ+β)<1,模型(2)的无病平衡点p0为局部渐近稳定的.



p(1+β-γ)I(t)
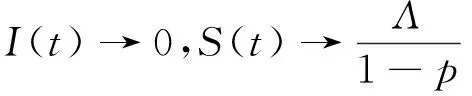
以下运用数学软件matlab数值模拟来验证地方病平衡点的稳定性.
当p(1-γ+β)>1时,参数Λ=10,p=0.9,β=0.3,γ=0.05,即R0=1.862 07>1,给定初值:
I(0)=25,S(0)=75,
I(0)=50,S(0)=50,
I(0)=75,S(0)=25,
可得到地方病平衡点的数值模拟结果,如图3所示.
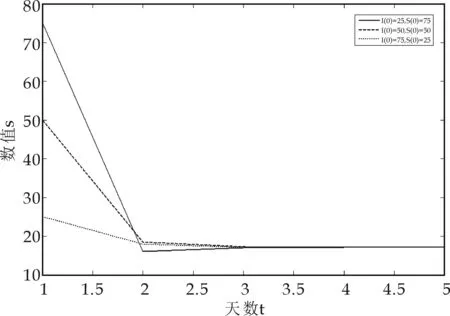
图3 易感者随时间变化趋势

4 持久性
下面我们讨论模型在R0>1时,模型(2)是持久[10]的.
定理3 当R0>1时,模型(2)是持久的.
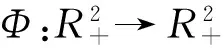
设M∂={(S(0),I(0))∈∂X0|Φt(S(0),I(t))∈∂X0,∀t≥0,t∈N},则M∂={(S,0)∈∂X0|S≥0}.事实上,{(S,0)∈∂X0|S≥0}⊆M∂,对于∀(S(0),I(0))∈M∂,可以判定I(t)=0,∀t≥0,t∈N恒成立.否则,存在T≥0,使I(t)>0,t≥T,t∈N.也就是,当取初值(S(0),I(0))∈M∂,则(S(t),I(t))∉M∂.根据以上分析,M∂={(S,0)∈∂X0|S≥0}成立,M∂中仅包含一个平衡点p0,且p0是渐近稳定的.

S1(t+1)=Λ+pS1(t)+pγε
(7)


对于给定的参数数值可得到地方病平衡点p1,且p1是集合X中的孤立不变集,并满足Ws(p1)∩X0=Ø,则集合M∂中的每一条轨道都趋近p1,并且p1在集合M∂中是非循环的.故存在δ>0,对∀(S(0),I(0))∈X0,满足:


5 小结
本文依据多个传染病模型[10-14]研究结果,给出了合理的模型假设,并对模型进行了分析和研究,得到SIS模型的无病平衡点和地方病平衡点,对无病平衡点和地方病平衡点的稳定性给出了判断.而由于方程求解的局限性,只能给出地方病平衡点存在唯一性.本文利用再生矩阵的方法,定义了基本再生数R0.当R0=1是系统的阈值,会根据分支理论再进一步讨论.本文主要论证系统的无病平衡点和地方病平衡点在R0>1和R0<1时的存在性和稳定性.
[1] Mena Lorca J,Hethcote H W.Dynamic models of infections diseases as regulators of population sizes[J].Journal of Mathematical Biology,1992,30(7):693-716.
[2] Capasso V,Serio G.A generalization of the kermack mcked rick deterministic epidemic model[J].Mathematical Biosciences,1978,42(1/2):43-61.
[3] 周义仓,曹 慧,肖燕妮.差分方程及其应用[M].北京:科学出版社,2014.
[4] Carlos Castillo Chavez,Abdul AzizYakubu.Dispersal, disease and life-history evolution[J].Mathematical Biosciences,2001,173:35-53.
[5] 刘纯英.几类高阶差分方程的动力学行为[D].兰州:兰州理工大学,2008.
[6] 龚德恩.经济控制论[M].北京:高等教育出版社,2009:65-68.
[7] Linda J.S.Allen,P.van den Driessche.The basic reproduction number in some discrete-time epidemic models[J].Journal of Difference Equations and Applications,2008,14:1 127-1 147.
[8] Cao H,Zhou Y C.The discrete age-structured SEIT model with application to tuberculosis transmission trends[J].Mathematical and Computer Modelling,2012,55:215-228.
[9] 蔺小林.现代数值分析方法[M].北京:科学出版社,2014.
[10] 曹 慧,王玉萍.具有饱和治愈率的离散SIS传染病模型的动力学性[J].陕西科技大学学报(自然科学版),2013,31(5):147-150.
[11] 曹 慧,周义仓.具有饱和治疗的离散SEIS结核病模型的动力学性态[J].数学的实践与认识,2014,44(18):209-216.
[12] 杨俊仙,闫 萍.一类具非线性发生率的SIQS传染病模型的动力学性态分析[J].浙江大学学报,2015,42(3):271-275.
[13] 陈 辉,徐 瑞.一类具有饱和发生率的离散型SIS传染病模型[J].军械工程学院学报,2014,26(5):70-74.
[14] 王 蕾,王 凯,张学良,等.具有标准发生率和因病死亡率的离散SIS传染病模型的全局稳定性分析[J].数学的实践与认识,2014,44(19):310-316.
【责任编辑:蒋亚儒】
The dynamics of discrete-time SIS model with exponential occurrence rate
MAO Hong-yan, CAO Hui, LIN Xiao-lin
(School of Arts and Sciences, Shaanxi University of Science & Technology, Xi′an 710021, China)
In this paper,the discrete-time SIS epidemic model with exponential occurrence rate is investigated.Using the renewable matrix method,we defined the basic reproductive number;The existence and stability conditions of equilibria and the persistence of SIS model are discussed.Numerical simulations are conducted to demonstrate our theoretical results.
SIS model; differential equation; equilibrium point; asymptotic stability
2016-03-11
国家自然科学基金项目(11301314); 陕西省科技厅自然科学基金项目(2014JQ1025); 陕西科技大学学术团队计划项目(2013XSD39)
毛红艳(1989-),女,河南叶县人,在读硕士研究生,研究方向:生物数学理论及应用
1000-5811(2016)05-0174-05
O151.21
A
