关于人体颈动脉硬化斑块诊断优化仿真
2016-05-10杨云,董雪,齐勇
杨 云, 董 雪, 齐 勇
(陕西科技大学 电气与信息工程学院, 陕西 西安 710021)
关于人体颈动脉硬化斑块诊断优化仿真
杨 云, 董 雪, 齐 勇
(陕西科技大学 电气与信息工程学院, 陕西 西安 710021)
人体颈动脉血流动力学数据与颈动脉硬化斑块形成有重要关联,其具有高维度、非线性等复杂属性.支持向量机算法在克服维数灾难问题和处理非线性数据上具有显著优势.基于该算法,首先通过多次实验得到在血流动力学信息中与颈动脉硬化斑块形成最为相关的属性子集,并对惩罚因子与核函数参数进行选择与优化,结果显示分类器性能有所提高,但并不明显,分类准确率只有58.2%;然后又通过集成学习将其准确率提升了17.3%,达到75.5%,所建立的诊断分类器可为临床提供一定的参考意见.
支持向量机; 颈动脉硬化斑块诊断; 性能优化; 性能评估
0 引言
颈动脉硬化多发于中老年人,最显著的特点是硬化斑块的形成,硬化斑块形成后可能导致动脉狭窄[1],而血管内血流状况的改变可能进一步改变动脉管壁上的压力使动脉狭窄更加严重,引起硬化斑块的破裂、脱落等,严重危害人们的生命健康[2].目前,颈动脉硬化斑块的诊断大多通过医生人工分析颈动脉多普勒超声所提供的信息来做出判断,这样复杂且高维的信息数据人脑很难处理[3],数据挖掘技术对高维且复杂的数据分析提供了有力支持,尤其是对缺少先验知识的医学数据.而少数利用BP(Back Propagation)算法来分析处理颈动脉超声数据的,又会带来过度拟合等问题[4,5],支持向量机在处理小样本、非线性数据时能避免BP算法所产生的过学习问题.因此,本研究采用高性能的支持向量机算法,对西安市唐都医院311例颈动脉硬化患者血流数据进行分析,建立颈动脉硬化斑块诊断分类器,并研究颈动脉硬化斑块的形成与血流动力学参数的关系.
1 人体颈动脉硬化斑块诊断分类器优化原理
优化该诊断分类器时主要有两个问题,一是支持向量机建立分类器时,它的核函数与参数的选择;二是单个的弱支持向量机分类器通常情况下分类效果不佳,针对该问题用集成学习的思想将弱分类器进一步优化提升.
在对支持向量机核函数与参数进行设置时总想要得到最好的参数组合,然而直到今天也没有一个能满足各种不同需要的参数设置的最好方法,一般在实际中经常会用到的解决办法就是把惩罚因子与核函数参数控制在一定范围内进行穷尽,用这种思想并通过某种评估方法,例如,本文所使用的20折交叉验证法对一定范围内的所有可能取值进行评估,然后选取最优的.
通常单个弱分类器的性能并不理想,集成学习的出现在一定程度上解决了用单个分类算法对数据集进行分类时性能不优的弊端,但这也受到了数据集质量与数量以及挖掘算法选用的是不是适合等问题的制约,但在大多数情况下与单个分类器相比较而言,集成分类器效果都会有所提高,它所依据的理论基础是统计技术中的迭加分类器,并用某种方式将许多单一分类器结合起来而取得比单个分类器更高的准确率.一个集成支持向量机示意图如图1所示.

图1 集成支持向量机
2 颈动脉斑块诊断分类器建立的方法
2.1 数据预处理
颈动脉硬化斑块诊断分类器建立过程中,首先,选取除血流动力学参数属性以外其他属性基本统一均衡的样本,如所选的311例样本中,有168例有硬化斑块,143例无硬化斑块,男性155例,女性156例,且年龄范围在50~70岁之间,电子病历显示他们均不患有其他疾病,该样本集中每一个样本对应一个病人的血流动力学参数以及斑块有无的诊断结果.
2.1.1 血流动力学数据规范化
颈动脉血流动力学参数包括以下属性:颈内动脉收缩期的峰值流速(IVmax)、舒张末期流速(IVmin)、收缩期与舒张期流速比值(IVmax/IVmin)、平均血流速度(ITAMAX)、搏动(IPI)、阻力指数(IRI),它们的数值范围如表1所示,椎动脉收缩期的峰值流速(VVmax)、舒张末期流速(VVmin)、收缩期与舒张期流速比值(VVmax/VVmin)、平均血流速度(VTAMAX)、搏动指数(VPI)、阻力指数(VRI),它们的数值范围如表2所示.

表1 颈内动脉各参数大小
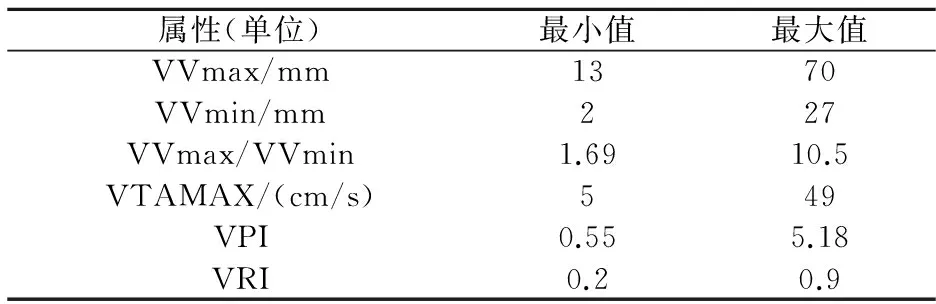
表2 椎动各脉参数大小
由表1和表2可知,12个数值属性范围与单位各不相同,因此要进行规范化处理,规范化能够有效避免某些过大属性值对较小属性值在建立分类器时的影响.使用数据挖掘工具WEKA的非监督过滤器(UnsupervisedFilter)下的Normalize规约发现,将整个数据集简单的规约至[0,1]之间分类效果很差,经过多次实验结果对比规约至[0,10]区间内更有利于支持向量机数据挖掘.该样本集中每一个实例都对应了一个病人的血流动力信息参数以及斑块有无的诊断结果分类标记分别记做‘1’,‘-1’,Weka给出实例斑块有无的诊断结果统计图如图2所示.
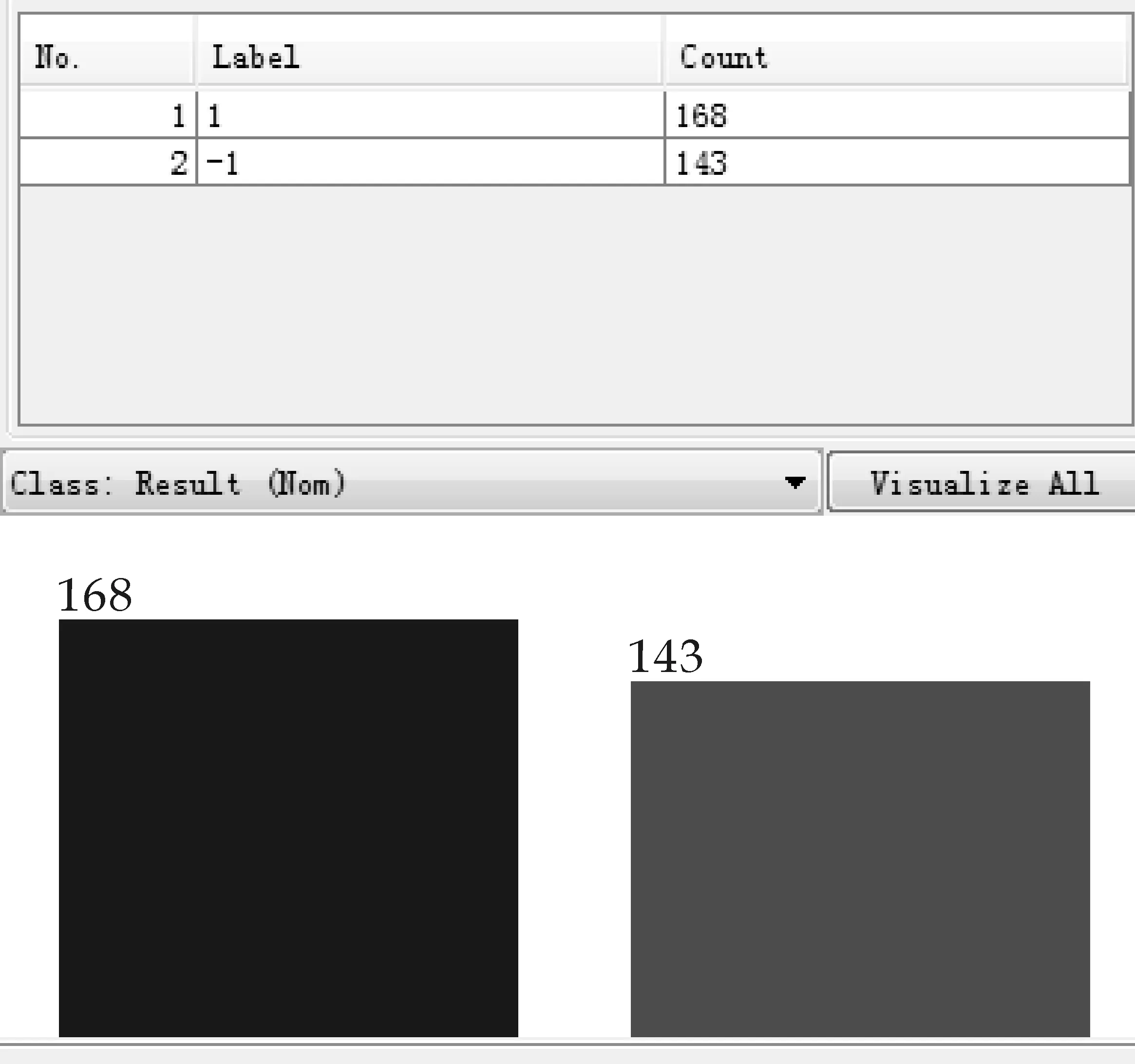
图2 诊断结果统计图
2.1.2 血流动力学参数属性过滤
属性选择作为数据预处理的一种重要方法对数据进行约减,在颈动脉血流动力学参数数据集的12个属性中,无关属性会对分类器建立造成负面影响,通常只保留最为相关的属性而去除冗余属性[6],这样既提高了算法性能又加快了算法运行速度[7,8].对血流动力学数据集进行离散处理,利用增益比率评价方法对不同属性与诊断之间的相关性进行评价.评价过程中采用Ranker搜索策略,可对每个属性的相关值由高到低的进行排序,并根据设定的阈值过滤掉部分属性.过对实验结果分析,得到血流动力学属性与颈动脉硬化斑块诊断相关性大小的排序为VPI>IVmax/IVmin>VVmax/VVmin>VVmax>VRI>IRI>IVmax>ITAMAX>IPI>VTAMAX>IVmin>VVmin.
由于Ranker的阈值难以确定,无法准确过滤属性,有时甚至过滤掉了能获得更好分类效果的属性子集,因此从相关性最小的属性VVmin开始依次向相关性增大的方向移除属性,形成13个属性子集,包括属性全集和空集,再用支持向量机进行验证,通过评估在13个属性子集上支持向量机的分类效果,来获得相关性最高并且属性个数最小的属性子集.选取Kappa统计量、平均绝对误差和均方根误差进行评估,其中Kappa统计量的值越大在该属性子集上的分类效果越好,而平均绝对误差和均方根误差则是数值越小分类器性能越好.以移除次数为横坐标,3个评估参数大小为纵坐标绘制3条曲线,如图3所示.

图3 支持向量机对属性子集评估结果
如上图所示,从属性全集开始,依次移除每个属性后,获得的第六个属性子集{VPI,IVmax/IVmin,VVmax/VVmin,VVmax,VRI,IRI,IVmax}有最大的Kappa统计量以及最小的平均绝对误差与均方根误差,此时所建立的分类器具有最好的分类效果,因此,该属性子集即为目标属性子集,而这7个属性是血流力学参数种与颈动脉硬化斑块形成最为相关的属性.
2.2 基于支持向量机的仿真实验
2.2.1 支持向量机原理
支持向量机(support vector machines,SVM) 是由Vapnik等提出的一类新型数据挖掘算法[9,10],它能利用线性分类器实现对非线性分类边界的描绘,主要用于小样本、非线性的分类和回归,在一定程度上解决了过学习和维数灾难等问题,广泛应用于基因分类、人脸识别等领域中[11,12].SVM的基本思想是对于二分类线性可分数据产生一个超平面w·x+b=0,其中w为权值向量,x为输入向量,b为偏置,超平面与样本点之间的间隔称为分离边缘,如图4所示.距离最优超平面最近的实例称为支持向量,支持向量是最难分类的数据点在支持向量机的运行中起着主导作用,SVM就是要找到使得分离边缘最大,也就是利用支持向量所定义的最优超平面,并且使样本点位于其两侧,因此要确定分离边缘最大时w和b的最优值(w0,b0),然而直接求得(w0,b0)不太可能,因此转化为如下的约束优化问题[13].

图4 最优超平面示意图
对于给定的训练样本
T={(x1,t1),…,(xp,tp)},p=1,2,…,p,xi∈Rn,tp∈(-1,1)
其中,tp∈(-1,1)为分类类别标识,为找到w0和b0,问题转化为使其在
tp(w·xp+b)≥1,p=1,2,…,P
(1)
约束条件下有最小的代价函数:

(2)
该代价函数是w的凸函数,因而保证了局部最优解一定是全局最优解[14],然后利用Lagrange系数法和KKT条件解得最优超平面为:
(3)

对于非线性可分数据引入了松弛变量ξp≥0 与惩罚因子C,与线性可分类似约束条件变为:
tp(w·xp+b)≥1-ξp,p=1,2,…,P
(4)
最小代价函数为:
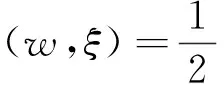
(5)
不同的是,非线性可分模式分类需将输入向量映射到一个高维特征向量空间,使大多数分线性可分模式在特征空间中可转化为线性可分模式,在特征空间构造最优超平面时,仅使用特征空间中的内积,根据泛函分析用满足Mercer定理的核函数K(xp,x),它就对应了某一转换空间的内积[15],因此,非线性可分的最优超平面为:
(6)
常用的核函数K(xp,x)有线性核函数、多项式核函数、Sigmoid核函数等,以及径向基核函数,分别定义为以下公式,即
K(xp,x)=x′*xp
(7)
K(xp,x)=[(x·xp)+1]q
(8)
K(xp,x)=tanh(k(x·xp)+1)
(9)
(10)
2.2.2 支持向量机参数优化
上述公式(7)、(8)、(9)、(10)中,除公式(7)没有参数,公式(8)需确定多项式核函数的最优阶数q,公式(9)中需确定Sigmoid核函数的宽度k,公式(10)中径向基核函数的宽度2δ2.此外还有支持向量机自身参数惩罚因子c,要分别与上述参数进行组合来确定整个支持向量机的参数设置.当使用线性核函数时只需优化惩罚因子c的值,所以使用Weka中的CVParameterSelection单个属性优化方法,将它在2-8~28之间按照步长为1进行搜索,得到最优的c为0.943 6;使用多项式核函数时,对(q,c)参数对优化时使用Weka中的网格搜索,将q在常用的1~10范围内,c在2-8~28内按步长为1进行搜索,得到q、c最优值为(3,0.999 9);使用Sigmoid核函数时,对(k,c)在2-8~28内进行同样搜索得到的最优值为(0.062 5、0.965 2);当使用径向基核函数时,对(2δ2,c)进行相同搜索得到最优值为(0.157 9、0.910 5).
通过上述过程,在一定范围内确保了各个核函数参数与惩罚因子组合的最优性,为建立支持向量机诊断分类器需选取其中能使支持向量机性能最优的一组参数作为最终参数组合,将20折交叉验证所得的平均绝对误差做为评判标准,结果如表3所示.由表3可知,当使用径向基核函数建立支持向量机时平均绝对误差值分别低于线性、所项式以及Sigmoid核函数7.4%、0.4%、7.1%,所以选择径向基核函数建立支持向量机.

表3 核函数参数与平均绝对误差
2.2.3 集成学习优化
集成学习中有装袋法与提升法两种不同的方法可对分类器集成.装袋法中生成的每个分类器彼此之间都是独立的,而提升法中则是迭代的生成每个分类器并且生成过程中后一个都要受到前一个的影响,它还会为所生成的各个分类器赋予不同的权值大小.它们都是用投票法将多个单一分类器的结果综合在一起.与提升法相比,装袋法更侧重用防止过度拟合的发生,而提升法更注重提高分类器的性能,为提高颈动脉硬化斑块分类器的准确度采用提升法中最具代表性的Adaboost算法来对准确率进行改善,该算法的流程图如图5所示.在Adaboost算法中需要确定迭代次数,进行30次实验并将平均绝对误差作为评价标准,结果如图6所示.由图6可知,迭代次数为15次的时候,平均绝对误差最小,最小值为0.242 8,在进行更多次的迭代时误差值趋于平稳,所以此时所建立的集成支持向量机的性能最优.

图5 Adaboost算法流程图

图6 平均绝对误差随迭代次数变化图
3 仿真结果
对仿真结果进行分析时,首先对BP算法与支持向量机算法结果进行比较;其次将默认参数与优化后的参数进行对比;最后对集成优化后的分类器性能进一步比较.评估方法都采用20折交叉验证.
3.1 BP算法与支持向量机结果对比
将Weka中默认参数下的BP算法与默认参数下的支持向量机所得评估结果进行统计,结果如表4所示.由表4可以看出,支持向量机的分类准确率高于BP算法8.04%,平均绝对误差、均方根误差与相对均方根误差低于BP算法8.1%、5.9%、16.56%,因此在颈动脉血流信息数据集上支持向量机的性能优于BP算法.

表4 核函数参数与平均绝对误差
3.2 参数优化后结果对比
选择径向基核函数建立支持向量机时,Weka中参数2δ2与c默认值为(0,1),优化后的值为(0.157 9,0.910 5),将二者的评估参数进行对比,结果如表5所示.由该表可知,默认值时的平均绝对误差、均方根误差与相对均方根误差分别高于优化后的参数3.5%、12.5%、6.1%,因此通过网格搜索后参数的确得到了优化.但只是参数优化对分类器的性能提升并不显著,所以进行集成优化.

表5 核函数参数与平均绝对误差
3.3 集成优化后结果对比
将优化前单个支持向量机与优化后集成支持向量机的评估参数进行统计,结果如表6所示.由表6可知,集成向量机正确分类率提高了17.3%,平均绝对误差降低了17.5%、均方根误差降低了10.1%,而相对均方根误差减少了34.01%.经过对比分析发现,对单个支持向量机集成优化后所建立的诊断分类器的各项误差值均有所降低.

表6 单个与集成支持向量机的评估参数
医学诊断性试验的质量通常用敏感性和特异性来衡量.敏感性是指在患病的人群中诊断结果是肯定的比例,特异性是指在没有病的人群中诊断结果是否定的比例,分别表示为公式(11)、(12).
FP/(FP+TN)
(11)
TN/(FP+TN)
(12)
式中:TN为正确的肯定,FP为错误的否定.
以敏感性为纵轴,特异性为横轴,将单个支持向量机与集成支持向量机的颈动脉硬化斑块诊断分类器的ROC曲线(Receiver Operating Characteristic Curve)同时绘制在图7中,曲线下面积记为AUC,当AUC>0.5时,AUC越接近于1,说明诊断效果越好;当且仅当AUC>0.5∧AUC<1时,分类器才是有价值的;AUC在0.9以上时分类器较准确.单个支持向量机的曲线下面积AUC=0.572,集成支持向量机的曲线下面积为AUC=0.75,进一步说明了集成优化后分类器性能得到了提高,并且该分类器具有一定的价值,而颈动脉血流动力学参数与颈动脉硬化斑块的形成有着密切联系.

图7 单个与集成支持向量机ROC曲线
4 结论
支持向量机可以实现对颈动脉血流动力学参数的信息融合与分析,在分类器建立过程中,经过属性过滤得到了血流动力学信息集中与颈动脉硬化斑块形成最为相关的属性子集.在使用支持向量机建立分类器时用穷尽的思想在一定范围内对其核函数参数与惩罚因子经过选择优化,发现分类器性能有所提高,而后通过集成优化使得分类器的性能得到了很大的提升.通过所建分类器可知,颈动脉硬化斑块的形成与颈动脉血流动力学参数有着密切的关系,在临床中虽不能仅凭血流动力学参数做出诊断,但也应当充分考虑血流动力学参数带来的影响.
[1] 白志勇,李敬府,杨玉杰,等.颈动脉粥样硬化斑块超声造
影特征分析[J].中国超声医学杂志,2011,27(11):994-996,1 044.
[2] 杨 鑫.三维超声图像中颈动脉粥样硬化的表型量化与分析[D].武汉:华中科技大学,2013.
[3] 孙海燕,黄品同,黄福光,等.超声造影评价颈动脉粥样硬化斑块的初步研究[J].中华超声影像学杂志,2007,16(3):219-221.
[4] 诸 毅.超声颈动脉血流量测量系统设计[D].上海:复旦大学,2004.
[5] 郭 翌.超声信息分析及其在动脉粥样硬化判别中的应用[D].上海:复旦大学,2008.
[6] Alagugowri.S,D R.T.Christopher.Enhanced heart disease analysis and prediction system [EHDAPS] using data mining[J].International Journal of Emerging Trends in Science and Technology,2014,9(1):1 555-1 556.
[7] Kennethr,Robertk,Joseph.Machine learning,medical diagnosis,and biomedical engineering research-commentary[J].Biomedical Engineering OnLine,2014,13(1):94-103.
[8] Golino H F,Amaral L S B,Duarte S F P,et al.Predicting increased blood pressure using machine learning[J].Journal of Obesity,2014,6(2):99-103.
[9] 顾成扬,吴小俊.基于EST和SVM的乳腺癌识别新方法[J].计算机工程与应用,2011,47(8):183-185,193.
[10] Jose M,Pablo E,Carlo B,et al.Prediction of the hemoglobin level in hemodialysis patients using machine learning techniques[J].Computer Methods and Programs in Biomedicine,2014,117(2):208-217.
[11] 顾亚祥,丁世飞.支持向量机研究进展[J].计算机科学,2011,38(2):14-17.
[12] Mattia C F Prosperi,Susana Marinho.Predicting phenotypes of asthma and eczema with machine learning[J]. BMC Medical Genomics,2014,7(1):82-88.
[13] 丁世飞,齐丙娟,谭红艳,等.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1):1-10.
[14] 程 然.最小二乘支持向量机的研究和应用[D].哈尔滨:哈尔滨工业大学,2013.
[15] 杨雯斌.支持向量机在大规模数据中的应用研究[D].上海:华东理工大学,2013.
【责任编辑:蒋亚儒】
Research on carotid atherosclerotic plaque diagnosis basd on SVM
YANG Yun, DONG Xue, QI Yong
(College of Electrical and Information Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China)
There is an important link between human carotid artery hemodynamic data and carotid atherosclerotic plaque formation, the hemodynamic data has high dimension and nonlinear attributes. The support vector machine algorithm has significant advantages in overcoming the curse of dimensionality and nonlinear data processing. Based on this algorithm. Firstly, the most relevant attributes subset of the hemodynamic data is obtained through many experiments. Secondly, the parameters of the cost and the kernel functions are selected and optimized. The results show that the classifier performance has improved, but not obviously. The accuracy is only 58.2%. And then through the ensemble learning the accuracy increased by 17.3%, and the final classification accuracy is 75.5%, the established diagnostic model can provide some references for clinical treatment.
SVM; carotid angiosclerosis plaque; classifier optimization; classifier performance
2016-04-20
陕西省科技厅科学技术研究发展计划项目(2014K15-03-06); 西安市科技计划项目 (NC1403(2),NC1319(1))
杨 云 (1965-),女,陕西咸阳人,教授,博士,研究方向:数据仓库与数据挖掘
1000-5811(2016)05-0162-06
TP391.9
A
