Relativistic Correction on Neutrino Emission from Neutron Stars in Various Parameter Sets∗

2016-05-10WenBoDing丁文波ZhanQiangQi戚湛强JiaWeiHou侯佳为GengMi密更TmurbaganBao特木尔巴根ZiYu喻孜GuangZhouLiu刘广洲andEnGuangZhao赵恩广

Communications in Theoretical Physics 2016年10期

Wen-Bo Ding(丁文波), Zhan-Qiang Qi(戚湛强),Jia-Wei Hou(侯佳为),Geng Mi(密更), Tmurbagan Bao(特木尔巴根),Zi Yu(喻孜),Guang-Zhou Liu(刘广洲),and En-Guang Zhao(赵恩广)

1College of Mathematics and Physics,Bohai University,Jinzhou 121000,China

2College of Chemistry,Chemical Engineering and Food Safety,Bohai University,Jinzhou 121000,China

3College of Physics And Electronic Information,Inner Mongolia University For The Nationalities,Tongliao 028043,China

4College of Science,Nanjing Forestry University,Nanjing 210037,China

5Center for Theoretical Physics,Jilin University,Changchun 130023,China

6Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China

1 Introduction

The neutron stars(NSs)are some tiny stars with the radii of about 10 km,however,their masses are aroundMsol∼2Msol.These characters make them an ideal laboratory for people to study extreme interactions and the nature of dense matter.[1−5]As the remnant of supernova explosion,NS was quite hot at initial,and the temperature could be as high as(1011–1012)K.Then the temperature was reduced to 1010K only in a few minutes by emitting neutrinos.In the first 106–107years of the lifetime of NS,the cooling is mainly realized by neutrino emission,which can be divided into two types:enhanced neutrino processes and standard neutrino processes.The enhanced neutrino processes include nucleon direct Urca(dUrca)process,hyperon direct Urca process,antikaon condensation direct Urca process,etc.,and among which dUrca process is the most effective cooling method in NS.[6−11]Researches have shown that the emissivity of enhanced neutrino processes is 103∼105times larger than that of standard neutrino processes,which may be neglected in some studies.Therefore for majority of NSs,neutrino emission due to dUrca process is mainly responsible for the cooling.

So far,there has been two forms of expression of the neutrino emissivity.The one is non-relativistic form,which was put forward by Prakash and Lattimer in 1991;[10]the other one is the relativistic form,which was proposed by Leinson in 2001.[12]Obviously,it is necessary to calculate the neutrino emissivity using this relativistic manner,which can make the numerical results more reliable,as the motion of the nucleons and leptons which participate in dUrca process in the star are relativistic,due to the high threshold density of the dUrca process,roughly 2n0(n0denotes the normal nuclear matter density).[13]However,majority of previous work related to neutrino emissivity have been done through the non-relativistic way.So it is meaningful to evaluate the relativistic correction on the neutrino emission,and make the previous non-relativistic results more available.

It is known that properties of neutron star matter are quite different from various parameter sets due to the uncertainty when extrapolating the equation of state(EoS)fromn0to high densities.For example,GM1 parameter set leads to a sti ffEoS and 2.34MsolNS can be obtained,whereas GPS250 set leads to a soft EoS and the maximum neutron star mass is as low as 1.98Msol.The EoS,neutrino emissivity,neutrino luminosity and cooling characteristics,which are related to the NS cooling,all depend on the choice of parameters.So different parameter sets will give quite different data results.Therefore in the paper,we will calculate the disparity in NS cooling properties between relativistic and non-relativistic ways in four classical parameter sets:GL85,GM1,GPS250,and GPS300 to get a general conclusion of relativistic correction on NS cooling.

This paper is arranged as follows.The details of our theoretical model are presented in Sec.2,and the numerical results and discussion are showed in Sec.3.Conclusions are given in Sec.4.

2 Models

We adopt the standard form of relativistic mean field theory(RMFT)to describe the properties of neutron star matter.[2,14−16]The Lagrangian density for the system takes the form(see Refs.[17–18]for details),

Here the baryons B include protons p and neutrons n,the leptons l include electrons e,and muonsµ.Three meson field equations can be acquired by solving the Euler-Lagrange equation,

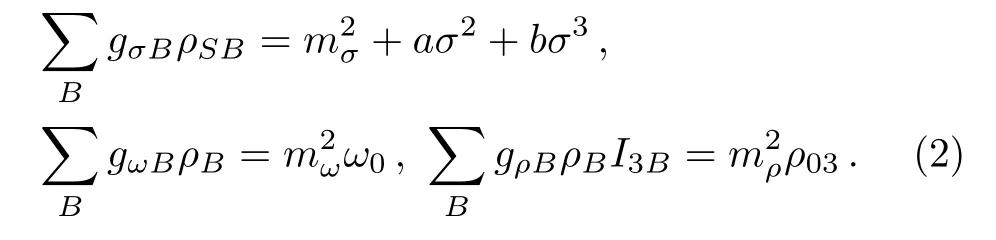
The related detail can be found in Refs.[17–18].Under the conditions ofβequilibrium and charge neutrality,the chemical potential is satis fied with this form,

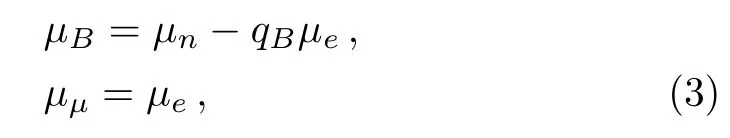
in whichqBrepresents the charged quantity of baryons.µB,µn,µeandµµare the chemical potentials of nucleons,neutrons,electrons and muons,respectively.For NSs,the electrically neutral and baryon number conservation must be obeyed,

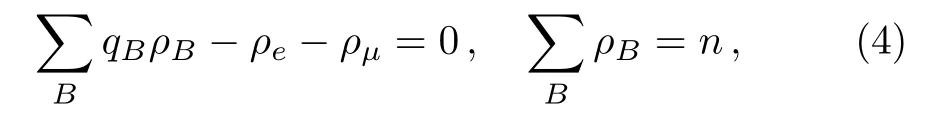
whereρB,ρe,ρµandnare number densities of nucleons,electrons and muons,and the total baryonic density,respectively.So at a fixed density,we can obtain the properties of neutron star matter by solving the above equations.Then using the Tolman–Oppenheimer–Volko ff(TOV)equations[19]we can obtain the static neutron star sequences.

The dUrca process consists of two successive reactions,βdecay and lepton capture,

And the corresponding relativistic neutrino emissivity[12]can be written as

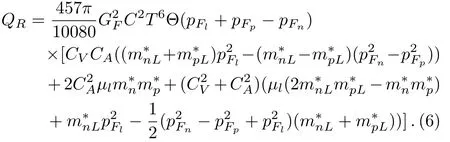
HereGF=1.436×10−49erg·cm−3represents the weakcoupling constant,andC=cosθc=0.973 is Cabibbo factor.CV=1 andCA=1.26 are the vector and axialvector constants.andin Eq.(6)represent Landau effective masses of neutrons and protons,which can be expressed in RMFT as

Whileis Dirac effective mass,which can be written as

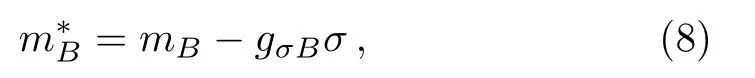
wheregσBis the coupling constant ofσfield and nucleons.pFl,pFp,pFnin Eqs.(6)–(7)are the Fermi momenta of lepton,proton and neutron,and Θ=1 if the Fermi momenta satisfy the triangle condition,

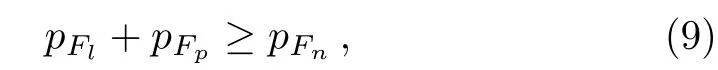
otherwise Θ=0,meaning dUrca process is not allowed.The non-relativistic neutrino emissivity[10]is

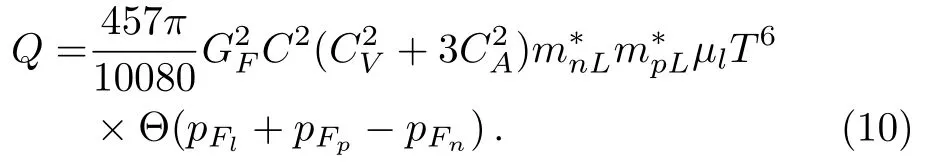
The cooling curves of NSs can be obtained by solving the cooling equation

in whichTandCvare the interior temperature and heat capacity of NS respectively.LνandLrrepresent the neutrino and photon luminosity.ForLγ,we use the empirical formulation,

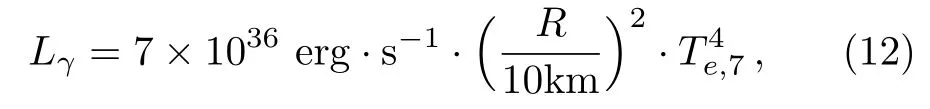
whereTe,7=Te×10−7,andTeis the effective surface temperature,

3 Discussion

In this paper,related to strong interaction,we consider conventional neutron star matter,which includes neutrons,protons,electrons and muons.To compare results roundly,four typical parameter sets:GL85,GM1,GPS250 and GPS300 are used,and the characters of parameters atn0can be seen in Refs.[2,14,20].

According to Eqs.(6)and(9),neutrino emissivityQdue to dUrca process as a function of the density in conventional neutron star matter with four parameter sets(GL85,GM1,GPS250,and GPS300)are shown in Fig.1.It is seen both relativistic and non-relativistic neutrino emissivity increase with the density.At low densities,there is a point corresponding to the considerable raise inQon each curve,meaning the occurrence of dUrca process withµ(dUrcaµprocess),which doubles the neutrino emissivity.However,the critical densities of dUrca processes with both electrons(dUrcae process)and muons are different in various parameter sets(also see Table 1),and GL85 set leads to the lowest critical densities,whereas GPS300 set leads to the highest.This is because the increasing speeds ofpFlandpFpin GL85 set are the fastest in the four sets,leading the trangle condition Eq.(9)to be ful filled at relatively low densities.It is found in Fig.1 that relativistic correction on neutrino emission lowers the magnitude ofQin all the four sets.At the maximum central density in every set,results show that relativistic correction leads to the lowest fall in GL85 set,however the biggest fall corresponds to GM1 set.Note that the disparity between relativistic and non-relativistic neutrino emissivity decreases with density,so the disparity on the maximum central density is actually almost the lowest for every parameter set.

Fig.1 (Color online)The relativistic(solid lines)and nonrelativistic(dashed lines)neutrino emissivity due to dUrca process in four parameter sets:GM1,GL85,GPS250 and GPS300.Here vertical dash-dotted lines correspond to the maximum central densities,and “R-” denotes relativistic results,whereas “NR-” means the exclusion of relativistic effect.

Combining with Eqs.(6),(9),(10)and the TOV equations,we can obtain the properties of neutrino emission in NSs.The critical masses of NSs for both dUrcae and dUrcaµprocesses in the four parameter sets are shown in Table 1,as well as the bulk properties of NSs and critical density of Urca process.It is seen that the mass range of NS where dUrcae or dUrcaµprocess can be allowed is quite different in various parameter sets due to the sensitivity of properties of NS matter to parameters.We find GL85 set favors the occurrence of dUrca process obviously in the four sets,for the critical masses of NSs for both dUrcae and dUrcaµprocesses are the lowest because of the low critical density in GL85 set(also see Fig.1).While the mass range of dUrca process in GPS300 set is the narrowest.Note that considering the consistent with observations,we ignore the NSs with the mass below 1.00Msol.

Neutrino emissivity due to dUrca process in NS interior with masses of 1.4Msoland 2.0Msolin various parameter sets are shown in Fig.2.It is found that neutrino emissivity declines with the increase of radial distanceR,and the relativistic Effect makes the neutrino emissivity lower,compared with the non-relativistic case.These results are also consistent with the relation between neutrino emissivity and density(see Fig.1).However,in the star with 1.4Msol(Fig.1(a)),it is seen that neutrino emissivity in GM1 set is much lower than that in the other parameter sets,and the low central density of the star is responsible for this phenomenon.In fact,the central density of 1.4Msolneutron star in GM1 set is only as small as 2.18n0,lower than the critical density of dUrcaµprocess(also see Table 1),consequently the absence of contribution of dUrcaµprocess leads to the very low magnitude ofQ.At the core of 1.4Msolstar,neutrino emissivityQin GPS300 set is the highest,however,at other radial range of the star,Qbecomes lower than that in GL85 and GPS250 sets.The main reason is the high critical density of dUrcaµprocess in GPS300 set,which makes the critical radial distance very small.The relativistic effect on neutrino emission is obvious in 1.4MsolNS.From calculating,we find that relativistic correction makes the neutrino emissivity decrease about 0.27,0.57,0.68 and 0.74 in units of 1erg·cm−3·s−1,meaning GPS300 set yields the strong relativistic Effect on neutrino emissivity.From Fig.2(b),we find the radial area where dUrca process is allowed becomes much wider in 2.0MsolNS than that in 1.4MsolNS due to the high density in 2.0MsolNS interior.And look from whole,the in fluence of relativistic Effect is deeper in 2.0MsolNS,compared with 1.4MsolNS.However,at the core of NS,the disparity ofQdue to relativistic correction is somewhat smaller in GL85,GPS250,and GPS300 sets.The reason is that the disparity falls with the density,which is showed in Fig.1.

Table 1 The maximum mass Mmax,central densities ucent=ncent/n0,radius R,the critical density of dUrca process for electrons ucdeand muons ucdµ,and mass ranges of NSs where dUrca processes of electrons and muons are allowed.

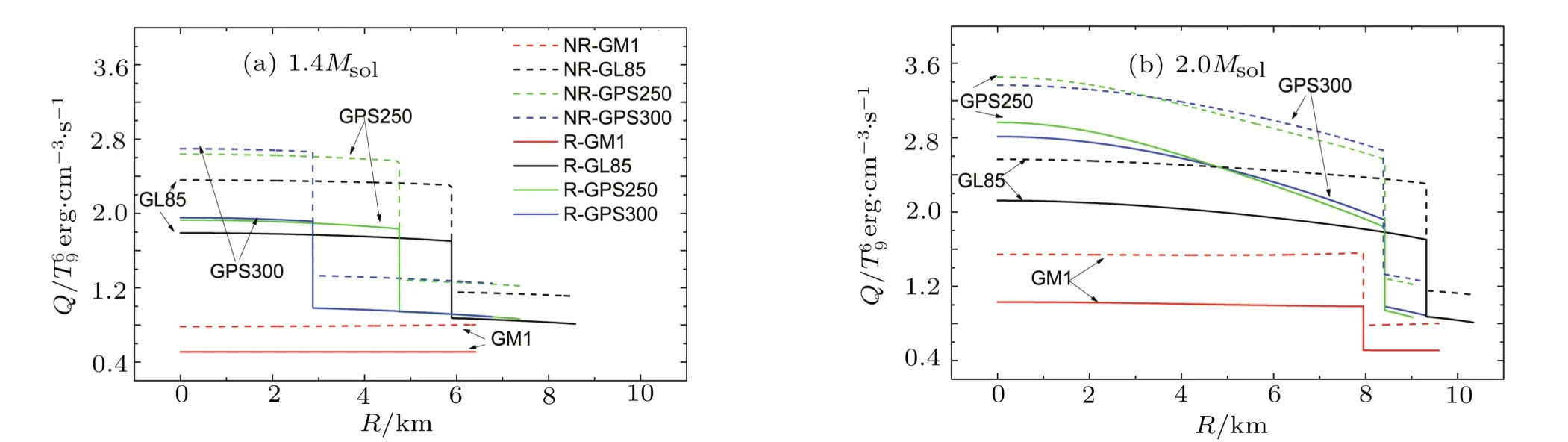
Fig.2(Color online)The relativistic(solid lines)and non-relativistic(dashed lines)neutrino emissivity due to dUrca processes in NSs with masses of 1.4Msoland 2.0Msolin the four parameter sets.Here R denotes the radial distance in NS.

Figure 3 shows the neutrino luminosity as a function of the mass of NS.It is seen that the maximum values of both relativistic and non-relativistic neutrino luminosity belong to GL85 set and the minimum ones belong to GM1 set.The relativistic Effect make neutrino luminosity decline obviously comparing with non-relativistic case.And the disparity between relativistic and non-relativistic neutrino luminosity grows with the mass of NS.This is reasonable,and the neutrino luminosity just reflect the overall relativistic Effect in NSs(see Fig.2).For example,the disparity of neutrino luminosity increases from 0.286 erg/s to 1.236 erg/s when the mass of NS is from 1.4Msolto 2.0Msolin GM1 set.And GM1 set leads to the largest decrease rate in the four sets,about 35 percents,whereas the other three sets lead about 25 percents fall.

By solving the cooling equation Eq.(11),we can obtain the cooling curves of NSs,as shown in Fig.4.It is found from Figs.4(a)and 4(b)that for each parameter set,relativistic cooling rate of NS is lower than non-relativistic one.And the difference in GM1 set is the most obvious in the four parameter sets.The large disparity of neutrino luminosity due to relativistic correction is mainly responsible for this result.It is found in Fig.4 that the difference of cooling rate in 2.0MsolNSs is bigger than that in 1.4Msol.For example,when the temperature of NS falls from 109K to 4×108K,in GM1 set,for 1.4MsolNS,the difference of time between relativistic and nonrelativistic Effect is about 150 years,whereas for 2.0MsolNS is about 200 years;in GL85 set,30 years and 80 years for 1.4Msoland 2.0MsolNS,respectively;in GPS250 set,50 and 70 years;in GPS300 set,50 and 80 years.From a theoretical point of view,the interior of massive neutron stars must exist tremendous gravitational field.And the general relativity is the theory which describes gravity,so the disparity between relativistic and non-relativistic effect is more obvious for massive neutron star.The above results mean the relativistic Effect on cooling rate in GM1 set is the strongest in the four sets.This result seems not to be consistent with Fig.2,however in fact the cooling rate is influenced by neutrino emissivity,properties of the NS,heat capacity and so on.So we conclude that the relativistic correction due to neutrino emission can be ignored for NSs with low masses in GL85 set.

Fig.3(Color online)The neutrino luminosity Lνas a function of the mass of NS in the four sets.

Fig.4(Color online)Cooling curves of temperature versus time for neutron stars with 1.4Msol(a)and 2.0Msol(b)in the four parameter sets.

4 Conclusion

In summary,we have investigated the relativistic correction on neutrino emissivity,neutrino luminosity and cooling rate in four typical parameter sets:GL85,GM1,GPS250,and GPS300.Results show that the mass range of NSs where dUrca process is allowed is the widest in GL85 set,whereas narrowest in GPS300 set,comparing with the other sets. Roughly speaking,relativistic effect makes the neutrino emissivity,neutrino luminosity and cooling rate lower,compared with the non-relativistic case.For neutrino emissivity,the biggest decrease due to relativistic correction is produced by GPS300 set.However,the largest fall in cooling rate corresponds to GM1 set.The influence of relativistic Effect grows with the mass of NS.And it is interesting that relativistic Effect can hardly influence the cooling rate of NSs with low masses(<1.4Msol)in GL85 set.

References

[1]J.Boguta,Phys.Lett.B106(1981)255.

[2]N.K.Glendenning and J.Schaner-Bielich,Phys.Rev.C60(1999)025803.

[3]S.E.Thorsett and D.Chakrabarty,Astrophys.J.512(1999)288.

[4]A.D.Kaminker,P.Haensel,and D.G.Yakovlev,Astron.&Astrophys.373(2001)17.

[5]D.G.Yakovlev,K.P.Leven fish,A.Y.Potekhin,et al.,Astron.&Astrophys.417(2004)169.

[6]Prakash,J.M.Lattimer,et al.,Astrophys.J.390(1992)77.

[7]P.Haensel and O.Y.Gnedin,Astron.&Astrophys.290(1994)458.

[8]D.G.Yakovlev,A.D.Kaminker,O.Y.Gnedin,et al.,Phys.Rep.354(2001)13.

[9]D.G.Yakovlev,A.D.Kaminker,P.Haensel,et al.,Astron.&Astrophys.389(2002)24.

[10]J.M.Lattimer,C.J.Pethick,M.Prakash,et al.,Phys.Rev.Lett.66(1991)2701.

[11]L.B.Leinson,Nucl.Phys.A707(2002)543.