Critical Behavior of Spatial Evolutionary Game with Altruistic to Spiteful Preferences on Two-Dimensional Lattices∗
2016-05-10BoYang杨波XiaoTengLi李晓腾WeiChen陈卫JianLiu刘剑andXiaoSongChen陈晓松
Bo Yang(杨波)Xiao-Teng Li(李晓腾)Wei Chen(陈卫)Jian Liu(刘剑)and Xiao-Song Chen(陈晓松)†
1Institute of Theoretical Physics,Key Laboratory of Theoretical Physics,Chinese Academy of Sciences,P.O.Box 2735,Beijing 100190,China
2School of Physical Sciences,University of Chinese Academy of Sciences,No.19A Yuquan Road,Beijing 100049,China
3Supercomputing Center of Chinese Academy of Sciences,Computer Network Information Center,Chinese Academy of Sciences,P.O.Box 349,Beijing 100190,China
4School of Science,Beijing Technology and Business University,Beijing 100048,China
1 Introduction
The spatial evolutionary game has been minutely studied to explain the emergence and maintenance of cooperation among selfish individuals during the past few years[1−4]in economics,biology and social sciences.
The structure of social networks and the evolutionary rules are two important research fields of evolutionary game.[5]Many interesting results have been obtained on different spatial structures,such as two-dimensional regular lattices,[6−7]small world networks[8]and scale-free networks.[9]Learning mechanism has been widely adopted in evolutionary rules.[5−7,9]Players revise their strategies by learning from their neighbors.Self-questioning mechanism is presented in Ref.[10].Each player adopts its anti-strategy to play a virtual game with all its neighbors,then obtains a virtual payoff.By comparing the real payoffand the virtual payoff,each player can get its optimal strategy corresponding to the highest payoff.[10−12]This evolutionary rule is similar to Ising model’s Metropolis algorithm in statistical physics.
Traditional economic theory predicts that individuals will not supply goods and services without being compensated.However,individuals do not always pursue selfinterest:people risking their own life to rescue others,soldiers participating in wars voluntarily,many kinds of charity etc.[13]Nowak summarized five possible rules for the evolution of cooperation corresponding to different situations:Kin selection,Direct reciprocity,Indirect reciprocity,Network reciprocity,Group selection.[4]In economics,altruistic and spiteful preferences have been introduced to study evolutionary stability of altruism and spitefulness.[13−16]In this paper,altruism,egoism and spitefulness are considered through a preference parameterp.Whenp>0,player is altruistic,which means a player has a positive regard for his opponents.p=0 represents the player as selfish.p<0 determines the player as spiteful.
In statistical physics,the internal energy decreases and approaches a minimum value at equilibrium in a closed system with constant external parameters and entropy(Principle of minimum energy).[17]Similarly,in economics,pro fit maximization is an eternal pursuit to the individual and society,so one may expect that the equilibrium probability distribution function of payoff s in a closed system of agents has the Boltzmann–Gibbs form.[18]In analogy to Ising model,spatial evolutionary game model can convert into Ising-like model,the effective Hamiltonian of evolutionary game can be obtained. By analyzing the effective Hamilton of game,game model is divided into three different phases:entirely cooperative phase(ferromagnetic order upward),entirely non-cooperative phase(ferromagnetic order downward),mixed phase(anti-ferromagnetic order)at zero social temperature(the noise introduced to permit irrational choices[6−7]).Two paths(the phase of game model translating from entirely cooperative phase to entirely noncooperative phase)are investigated.Continuous and discontinuous phase transitions are observed at sufficiently low temperature.Fourth-order cumulant is investigated to locate critical points.The critical exponents(ν,β,γ)are obtained by finite-size scaling.
This paper is organized as follows.In Sec.2,we make a brief review of Ising model with a nonzero field firstly,then we introduce our evolutionary game model and obtain the effective Hamilton of game model.Finally,the ground state of game model is divided into three phases in the condition of perfect rationality;in Sec.3,we present and discuss the results;in Sec.4,we draw a conclusions from the results.
2 Model
2.1 A Brief Review of Ising Model
The Hamiltonian of Ising model with an interactionJijfor any two adjacent sitesiandjand an external magnetic fieldhifor any siteiis given by

whereSiis the Ising spinat lattice sitei,the first sum is over pairs of adjacent spins(every pair is counted once).The notationindicates that sitesiandjare the nearest neighbors.
Ising models can be classi fied according to the sign of the interaction:forJij>0 the interaction is ferromagnetic and it is antiferromagnetic ifJij<0;whenJij=0,the spins are noninteracting.Additionally,the spin site wants to line up with the external field,forhi>0 the spin siteidesires to line up in the positive direction and it desires to line up in the negative direction ifhi<0;whenhi=0,there is no external in fluence on the spin site.Forhi=0,the Ising model is symmetric under switching the value of the spin in all the lattice sites,but a non zero field breaks this symmetry.The introduction of nonzero magnetic field destroys the continuous phase transition of the ferromagnetic Ising model,whereas the nonzero uniform field does not destroy the transition of the antiferromagnetic Ising model.The exact solution of antiferromagnetic Ising model in an external field can not be obtained.Instead,the researchers focus on the critical line(N´eel temperature as a function of external field)for the square lattice antiferromagnetic Ising in an external field.[19−23]For critical line,there are different approximations,[20,22,24]for example cosh(h/Tc)=sinh2(2J/Tc).The ends of the(T,h)critical line are(2.269,0)and(0,4|J|),and the antiferromagnetic phase is completely enclosed by transition lines.[25]
At zero temperature,a critical magnetic fieldhcexist in antiferromagnetic Ising model such ashc=4|J|for a square lattice.When−4J
In order to obtain energy difference∆E(iflips its directionEq.(1)can be rewritten as

wherekis a spin excepti.When the state ofiflips,the new energyE′is

Thus,the energy differenceis

2.2 Introduction of Game Model
For a randomly given agent i,two available strategies cooperation(Si=+1)and non-cooperation(Si=−1)can be adopted to play with its nearest neighbors.Mutual cooperation yields the rewarda,mutual non-cooperation leads to punishmentd,and the mixed choice gives the cooperator the suck’s payo ffband the non-cooperation the temptationc.
The randomly chosen playerirevises its strategy according to self-questioning mechanism and the stochastic evolutionary rule.That is to say,playeriadopts its antistrategy to play a virtual game with all its neighbors,and calculates the virtual payo ff.By comparing the real payoff and the virtual payo ff,player will find out its optimal strategy.[10−11]In next round,playeriwill revise its current strategy to its anti-strategy with a given probability

whereandare the real and virtual payo ffof playeri,respectively.The noise can be described viaT.TheGiis defined as

wheregirepresents the total payo ffof playeri(playeriplays with all its nearest neighbors and accumulates the obtained payoff).represents all its nearest neighbors’s total payoff by playing withi.pis preference parameter,positive denotes altruism,negative stands for spite,and zero characterizes classical own pro fit maximization.
This evolutionary rule is similar to single spin- flip of Ising model in statistical physics.We will find out the relationship between evolutionary game model and Ising model hereafter.
For a given agenti,the number of cooperative and non-cooperative neighbors areni+andni−,
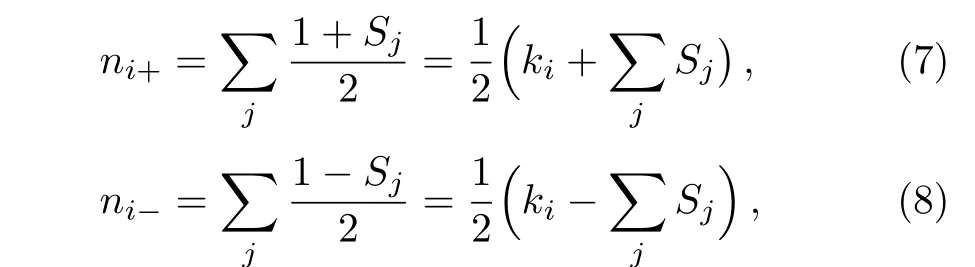
wherejis the neighbors set of agenti,kiis the sum of neighbors.
By playing the game with all its nearest neighbors,agentiacquires its payo ffgi. At the same time,its neighbors acquirein this process.WhenSi=+1,,andwhenSi=−1,and
In the process of virtual game(corresponding toiflips its direct in Ising),the payo ff s difference are∆giandThey can be calculated as
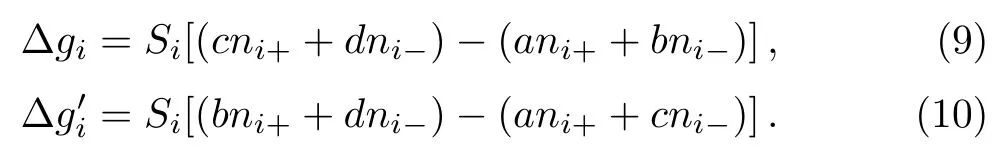
In our model,players care not only about their own monetary payoffs,but also about their opponent’s monetary payo ff s.Thus,the playidoes not necessarily maximize pay off itself,but rather weighted sums of own and opponent’s payoffs.The change of payoffs when the state ofiflips:can be written as,
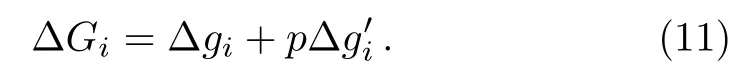
By substituting Eqs.(9)and(10)into Eq.(11),we obtain



As the Ising model,the strength of interactionJijand external fieldhican be defined as

The effective energy can be obtained

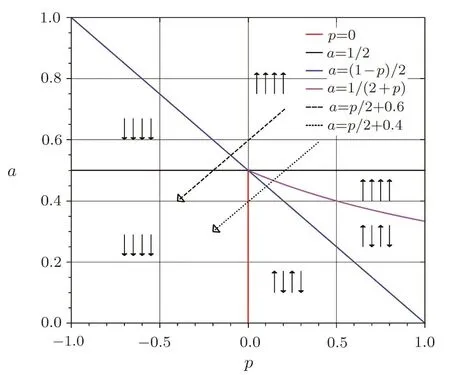
As a special accommodation,we investigate weak Prisoner’s Dilemma.We takea=a,b=0,c=1−a,d=0,and 1/3 For two-dimensional square lattices,ki=4,the effective energy is The ground state of game model at zero temperature can be divided though three equations:the strength of interactionJ=0,the external fieldh=0,and the critical external fieldh=4|J|.Results of these functions area=1/2 orp=−1 forJ=0;a=1/2(1−p)forh=0;a=1/(2+p)forh=−4J,andp=0 forh=4J,which are shown in Fig.1.Game model is divided into three phases:entirely cooperative phase(ferromagnetic order upward),entirely non-cooperative phase(ferromagnetic order downward),mixed phase(anti-ferromagnetic order).The region of cooperative and non-cooperative coexistence is enclosed by the critical lines(p=0 anda=1/(2+p)).In game model,Tis the measure of stochastic uncertainties(noise)allowing the irrational choices.ais an inherent parameter,which belongs the payoffmatrix.Whena>0.5,cooperation will gain much more benefit;whena<0.5,non-cooperation will get more.But cooperation can survive fora<0.5 owing to altruism.pas a preference parameter measures the relationship between spitefulness,egoism and altruism.Non-cooperation can arise only spitefulness existing. Fig.1 The ground state at zero temperature on the(a,p)parameter space.Three phases can exist:four small upward arrows denote entirely cooperative phase(ferromagnetic order upward),four small downward arrows denote entirely non-cooperative phase(ferromagnetic order downward)and small arrows upward and downward alternatively denote cooperative and noncooperative coexistence(antiferromagnetic order).The phase transition and critical phenomena are investigated by two special paths(two dashed lines),which cross cooperative and non-cooperative region. We have preformed Monte Carlo simulations on square lattice with periodic boundary conditions using Metropolis algorithm.The randomly chosen playerirevises its strategy according self-questioning rule.In general,we discarded the first 10000 Monte Carlo Steps(MCS)in order to achieve the stationary regime for all lattices sizes.In order to estimate the quantities of interest,we considered the next 2×105MCS to calculate the averages.To further improve accuracy,the final results are average over 100 independent realization with different initial con figurations. For antiferromagnetic Ising model,the staggered magnetization can be defined as which is the order parameter for antiferromagnetic systems.[26−27]The corresponding susceptibilities are defined by and the fourth-order Binder cumulants is wheremcan bemtormsforχ(m)andU(m). mt,ms,χ(m)andU(m)obey the following finite size scaling relations in the neighborhood of the stationary critical pointpc: whereis the critical preference parameter for a givenT. The derivative of fourth-order Binder cumulantsUL(p)is We can obtain the critical exponentνfrom a log-log plot ofversusL. In this model,the evolution of game model from entirely cooperative phase to entirely non-cooperative phase is an interesting problem,which involves the interaction between game’s parameteraand individual preferencepat low social temperatures.Thus,two special evolutionary pathsa=1/2p+0.6 anda=1/2p+0.4(broken lines in Fig.1)are taken.The patha=1/2p+0.4 passes through the antiferromagnetic region. In Fig.2,magnetisation as a function ofpfor several lattice sizesLis shown atT=0.002.The value of the magnetizationmtjumps from+1 to−1 as the preference parameterpis scanned from the positive direction to the negative direction by the patha=1/2p+0.6 of Fig.1.The order parameter of magnetisationmtis discontinuous.Obviously,the critical exponentβ/ν=0,indicate a discontinuous phase transition. Theoretically,the phase transition sweeping along patha=1/2p+0.6 is a transition from ferromagnetic order upward to ferromagnetic order downward.This is equivalent to a magnetic material placed in an external fieldh.If the temperature is lower thanTc(critical temperature at the intersection ofh=0 anda=1/2p+0.6),the value of the magnetizationmjumps from positive to negative as the external magnetic fieldhis scanned from the positive direction to the negative direction.Consider the 2D Ising model on a square lattice,the critical temperature isTc=2.269J=0.00225 at transition point(p=−0.1,a=0.55). Fig.2 Magnetisation as a function of p for several lattice sizes L along the path a=1/2p+0.6,magnetisation is discontinuous at transition point(p=−0.1,a=0.55). Fig.3 Staggered magnetization msfor various system sizes along the path a=1/2p+0.4 at T=0.02.Apparently,two critical points exist,because of the finite-size effects near p=0 and p=0.15 have been observed. In Fig.3,the order parameter of antimagnetisationmsas a function ofpfor several lattice sizesLis shown atT=0.02.The staggered magnetization changes with the lattice sizes near critical points.In Fig.4,susceptibility as a function ofpfor various system sizes is shown.The susceptibility has two maxima whose positions shift toward the corresponding critical points and their peaks increase with system sizeL.Those phenomena display remarkable finite-size effects.There are two critical points existing.To see them more clearly,we narrow down the range ofpto redraw the staggered magnetization(Figs.5 and 6)and susceptibility(Figs.7 and 8). Theoretically,patha=1/2p+0.4 intersects antiferromagnetic critical line. The antimagnetic phase transition is a second-order transition. In this situation,and the approximate critical line is cosh(2p−0.2/Tc) =sinh2[(p−0.2)(1+p)/(2Tc)].Two intersection can be obtained by solving this equation atTc=0.02,pc=0.01167 andpc=0.131426. Fig.4 Susceptibility as a function of p for various system sizes along the path a=1/2p+0.4 at T=0.02.The susceptibility has sharp jump near p=0 and p=0.15. Fig.5 The Staggered magnetization of the left critical point in Fig.3 near p=0. To locate the two critical points by using Monte Carlo simulations,we plot the reduced fourth-order cumulant,respectively.The fourth-order cumulant of the left phase transition point in Fig.3 is shown in Fig.9 as a function ofpfor several values ofL.The scaling relation for the fourth-order cumulant shows that,at the critical preference parameter,all curves must cross at a common point.From the crossing of these curves,we estimate the critical preference parameterpc=0.01127±0.00014.The fourth-order cumulant of the right phase transition point in Fig.3 is shown in Fig.10 as a function ofpfor several values ofL.The critical preference parameter ispc=0.13156±0.00008.Critical points are in good agreement with the one found from theoretical prediction(pc=0.01167 andpc=0.131426). Fig.6 The Staggered magnetization msof the right critical point in Fig.3 for various system sizes along the path a=1/2p+0.4 near p=0.15. Fig.7 The susceptibility of the left critical point in Fig.4 for varying lattice size near p=0. Fig.8 The susceptibility of the right critical point in Fig.4 as a function of p for various system sizes along the path a=1/2p+0.4 near p=0.15. Fig.9 Fourth-order cumulant UL(p)of the left critical point as a function of p.The intersection point is pc=0.01127±0.00014. Fig.10 Fourth-order cumulant UL(p)of the right critical point as a function of p for various system sizes and T=0.02.The intersection point is pc=0.13156±0.00008. In order to compare the critical phenomena with Ising model,we evaluate the critical exponents via finite size scaling relations in Fig.11.The log-log plots ofmL(p)as function ofLat the critical pointspc=0.01127 andpc=0.13156 are shown at Figs.11(a)and 11(b),respectively.The best fit to the data points furnishes the valueβ/ν=0.116±0.0093 atpc=0.01127.Whenpc=0.13156,the value isβ/ν=0.1135±0.00702.Figures 11(c)and 11(d)show the log-log plot of susceptibilityχL(pc)vs.Lat the critical pointspc=0.01127 andpc=0.13156,respectively. The slope of the fitting lines areγ/ν=1.749±0.0212 atpc=0.01127,andγ/ν=1.736±0.0405 atpc=0.13156.The loglog plots ofU′L(p)as function ofLat the critical pointspc=0.01127 andpc=0.13156 are shown at Figs.11(e)and 11(f),respectively.The solid lines are the best fit with slope 1/ν=0.977±0.0391 atpc=0.01127,and 1/ν=0.982±0.0296 atpc=0.13156. Fig.11 Log-log plot of staggered magnetization mL(pc)vs.L:(a)pc=0.01127,the slope of fitting line is−β/ν = −0.116± 0.0093;(b)pc=0.13156,the slope is−β/ν = −0.1135± 0.00702.Log-log plot of susceptibility χL(pc)vs.L:(c)pc=0.01127,the solid line is the best fit with slop γ/ν =1.749 ± 0.0212;(d)γ/ν=1.736±0.0405 at pc=0.13156.Log-log plot ofvs.L:(e)pc=0.01127,the solid line is the best fit with slop 1/ν=0.977±0.0391;(f)1/ν=0.982±0.0296 at pc=0.13156. A general game model about economical and social activities is proposed in this paper.We can relate this game model with Ising model in statistical mechanics.The interaction between spins and external field of the Ising model are determined by the rewardaof cooperation and the preference parameterp,which can be altruistic to spiteful.We have studied weak prisoner’s dilemma on a square lattice with periodic boundary condition.At zero social temperature without noise for irrational decision,there are three different phases:entirely cooperative phase(ferromagnetic order upward),entirely non-cooperative phase(ferromagnetic order downward),and mixed phase(anti-ferromagnetic order).In the investigation of evolution from entirely cooperative phase to entirely non-cooperative phase,two evolutionary pathsa=1/2p+0.6 anda=1/2p+0.4 have been taken.For the patha=1/2p+0.6,the sytem undergoes a discontinuous transition under a critical temperature.For the patha=1/2p+0.4,there are two continuous phase transitions at the critical pointspc=0.01127 andpc=0.13156 respectively.The critical exponentsβ/ν,γ/νand 1/νare estimated for the two critical points at a fixed reduced temperatureT=0.02.Within the error range of data,the critical exponents atpc=0.01127 andpc=0.13156 are the same and equal to the results of two-dimensional Ising model.These results indicate that the continuous phase transitions of the game model belong to the same universal class as the two-dimensional Ising model. References [1]1234 R.Axelrod,The Evolution of Cooperation,Basic Books,New York(1984). [2]M.A.Nowak and R.M.May,Nature(London)359(1992)826. [3]M.A.Nowak,Evolutionary Dynamics:Exploring theEquations of Life,Harvard University Press,Harvard,MA(2006). [4]M.A.Nowak,Science314(2006)1560. [5]G.Szab´o and G.F´ath,Phys.Rep.446(2007)97. [6]G.Szab´o and C.T˝oke,Phys.Rev.E58(1998)69. [7]G.Szab´o,J.Vukov,and A.Szolnoki,Phys.Rev.E72(2005)047107. [8]J.Vukov,G.Szab´o,and A.Szolnoki,Phys.Rev.E77(2008)026109. [9]F.C.Santos and J.M.Pacheco,Phys.Rev.Lett.95(2005)098104. [10]W.X.Wang,J.Ren,G.R.Chen,and B.H.Wang,Phys.Rev.E74(2006)056113. [11]K.Gao,W.X.Wang,and B.H.Wang,Physica A380(2007)528. [12]Y.K.Liu,Z.Li,X.J.Chen,and L.Wang,Chin.Phys.Lett.26(2009)088902. [13]H.Bester and W.G¨uth,J.Econ.Behav.Organ.34(1998)193. [14]A.Possajennikov,J.Econ.Behav.Organ.42(2000)125. [15]D.K.Levine,Rev.Econ.Dynam.1(1998)593. [16]F.Bolle and A.Kritikos,Theory Dec.60(2006)371. [17]H.B.Callen,Thermodynamics and an Introduction to Thermostatistics,(2nd).,John Wiley&Sons,New York(1985). [18]Q.Zhuang,Z.R.Di,and J.S.Wu,PloS ONE9(2014)e105391. [19]L.Onsager,Phys.Rev.65(1944)117. [20]E.M¨uller-Hartmann and J.Zittartz,Z.Phys.B27(1977)261. [21]X.N.Wu and F.Y.Wu,Phys.Lett.A144(1990)123. [22]X.Z.Wang and J.S.Kim,Phys.Rev.Lett.78(1997)413. [23]S.Y.Kim and J.Korean,Phys.Soc.61(2012)1950. [24]S.J.Penney,V.K.Cumyn,and D.D.Betts,Physica A330(2003)507. [25]M.E.Fisher,Rep.Prog.Phys.30(1967)615. [26]J.P.Neirotti and M.J.de Oliveira,Phys.Rev.B54(1996)6351. [27]M.Godoy and W.Figueiredo,Phys.Rev.E65(2002)026111.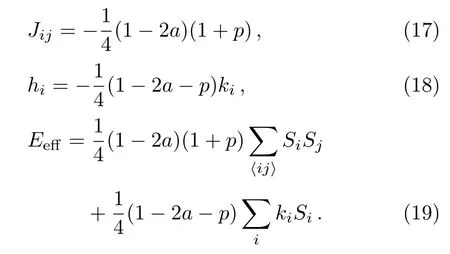

2.3 Three Phases of Game Model
3 Results and Discussions

















4 Conclusions
猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Relativistic Correction on Neutrino Emission from Neutron Stars in Various Parameter Sets∗
- Study of Friction between Liquid Crystals and Crystalline Surfaces by Molecular Dynamic Simulations∗
- A Complex Network Model for Analyzing Railway Accidents Based on the Maximal Information Coefficient∗
- E ff ect of Mis fit Strain on Pyroelectric Properties of(111)Oriented Pb(Zr1−xTix)O3 Thin Films∗
- First-Principles Study of Structural,Magnetic,Electronic and Elastic Properties of PuC2∗
- In fluence of Defects and Crystallographic Orientation on Mechanical Behavior of Nanocrystalline Aluminium∗
