Semi-Relativistic Reflection and Transmission Coefficients for Two Spinless Particles Separated by a Rectangular-Shaped Potential Barrier
2016-05-10ThylweOluwadareandOyewumi
K.E.Thylwe,O.J.Oluwadare,and K.J.Oyewumi
1KTH-Mechanics,Royal institute of Technology,S-100 44 Stockholm,Sweden
2Department of Physics,Federal University Oye-Ekiti,P.M.B.373,Ekiti State,Nigeria
3Theoretical Physics Section,Department of Physics,University of Ilorin,P.M.B.1515,Ilorin,Nigeria
1 Introduction
The simplest models used for theoretical predictions of a transmission coefficient are taken from non-relativistic quantum mechanics describing a single mass particle approaching a repulsive potential barrier in one space dimension.
The non-relativistic quantum theory of relative motion of particles does not take into account two-body phenomena.It predicts the same results for any two particles with the same,common reduced mass.Two-body effects have to do withrelativisticconsiderations;special relativity.Two-body effects may be;energy shifts of resonances and bound states,and even disappearance of exited bound states.Such relativistic effects exist for a single Dirac mass in a potential,described by Dirac theory.[1]In the present study spin is ignored and focus is on the role of different two-body mass combinations.

A recent analysis of the two-body barrier problem in(1+1)dimensions was treated by the so called spinless Salpeter(SSE)equation.[5]This equation results from a Schr¨odinger-type approximation of the SRQ-equation due to Ikhdair&Sever,[2]primarily for obtaining discrete energy spectra.The method has been applied to several bound-state problems[6]and some of its results have been discussed and questioned by Lucha&Sch¨oberl.[3]In the present scattering context the same approximation will be referred to as the generalized Schr¨odinger(GS)approximation.
The present study is limited to scattering in(1+1)relativistic dimension of two spinless particle masses.Exact results for the rectangular potential model are compared to results based on the generalized Schr¨odinger(GS-)approximation and those of the non-relativistic Schr¨odinger approximation.The non-relativistic Schr¨odinger theory depends only on the reduced mass of the particles.Therefore,it is instructive to present two-body results with a given reduced mass.
The potential is given by
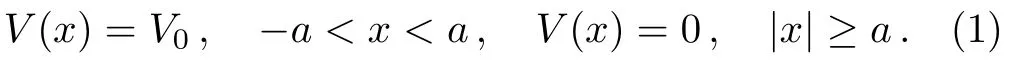
A limit for the potential strengthV0is introduced,having to do with the physical understanding of the scattering results.The potential rangeais varied,as it appears to be particularly important for the occurrence of oscillations in the transmission coefficient as function of the scattering energy.
Section 2 formulates the semi-relativistic two-body problem.Section 3 presents an analytic solution of the non-relativistic and the generalized Schr¨odinger problems for the potential model used.Illustrations and results are presented in Sec.4.Conclusions are given in Sec.5.
2 Quantum-Mechanical Two-Particle Equations with Relativistic Corrections
The total linear momentum is conserved and the centre-of-mass relative momenta are related by the classical vector equationp2=−p1.Therefore,a single operator symbolˆp=−i~d/dxis introduced,~being the reduced Planck’s constant.This operator describes the relative motion of two particles with massesm1andm2along anx-axis in a center-of-mass reference system.The SRQ-wave functionψfor the relative motion satisfies the equation[3]

whereis the total energy,andϵis the(non-rest)scattering energy.
In regions of no interaction potential,the free wave(a plane waveψk=eikx)satisfies

wherekis the “free” wave number away from the barrier.This implies,by expanding the square-root operators in Eq.(2),that

wherem=m1+m2is the total mass.
In the asymptotic(potential-free)regions,the relation between the wave number and the energy is or equivalently
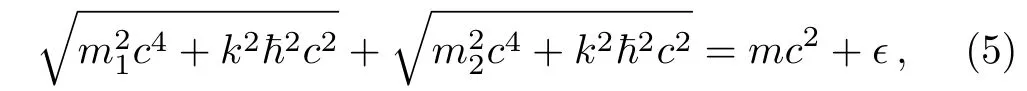
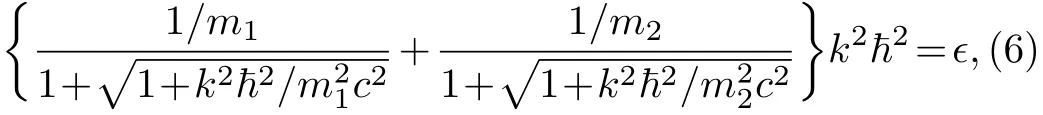
obtained by standard algebraic manipulations.
By solving Eq.(5)(or Eq.(6))for the asymptotic wave number,one obtains
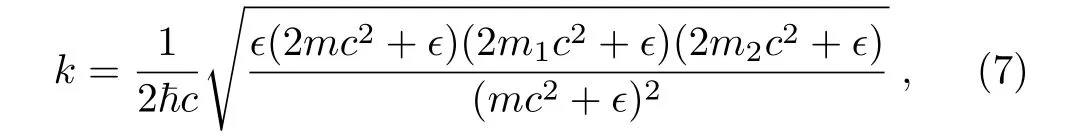
which reduces to the non-relativistic(NR)expression(asc→+∞)
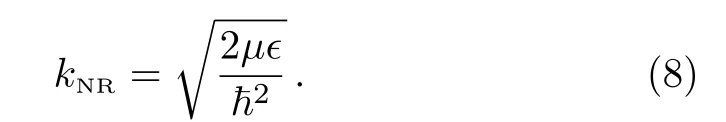
whereµis the reduced mass
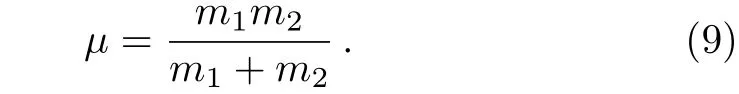
The wave numberskandkNRare positive for allϵ>0.
In the barrier region of the rectangular potential(1)the wave number of a plane wave is denotedkB,and is given by
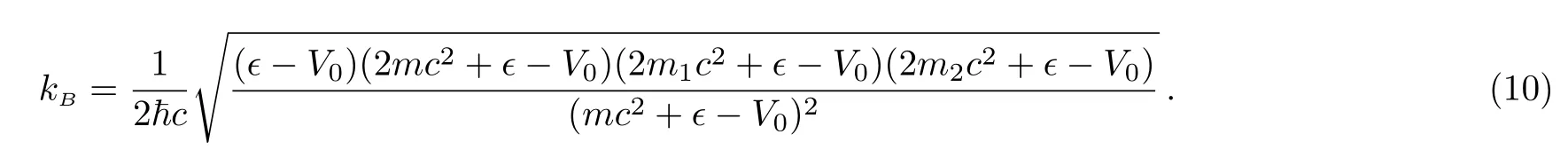
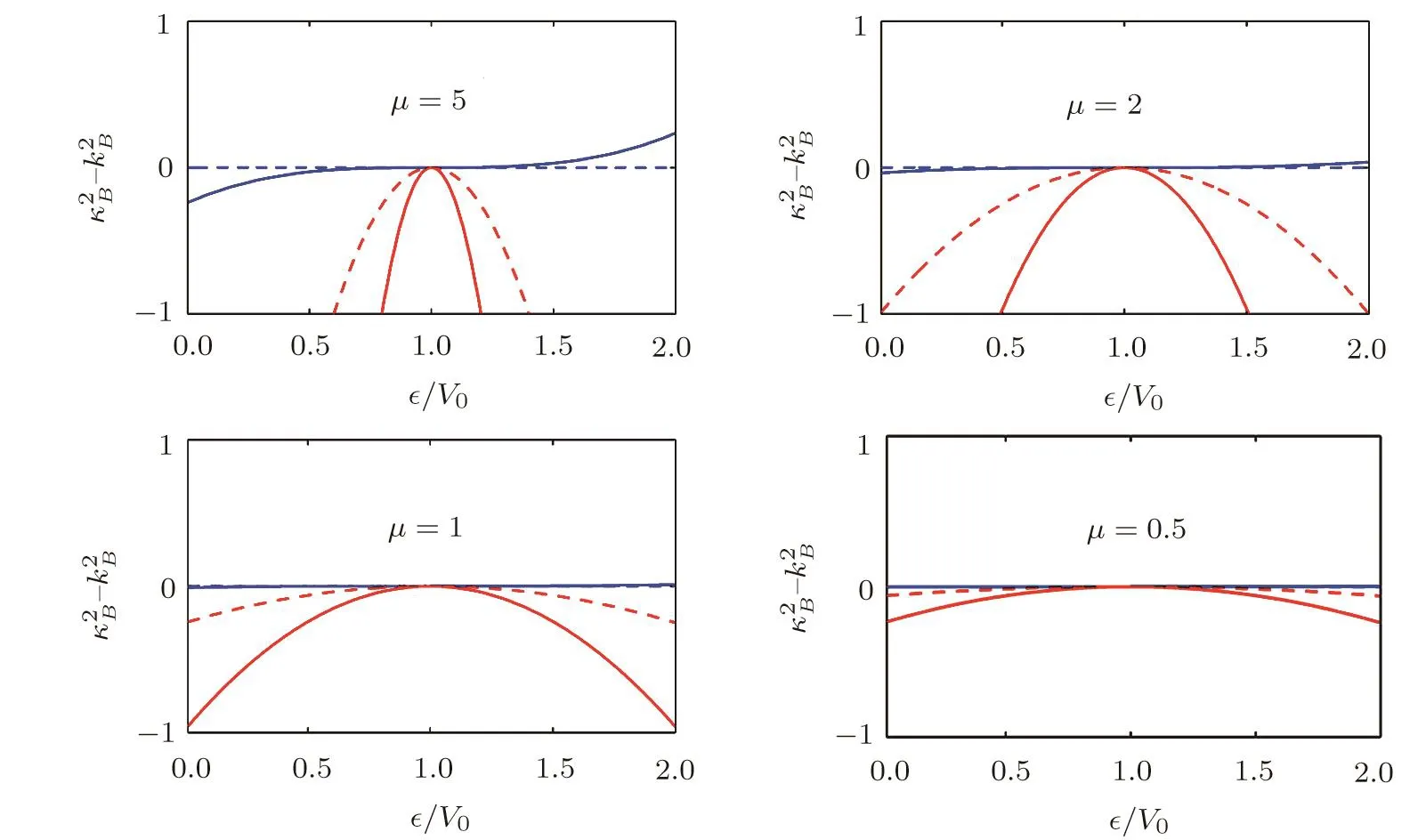
The wave numberkBis either real or imaginary.It is positive forV0−ϵ<0.It may also turn real at a second energy range for which physical intuition is not obvious.More specifically,kBis positive also forwherem2is the smaller mass of the particles.For equal masses this second positive branch ofkBdoes not exist.Note that,if masses are different,there is also a singular value ofkBin the second energy branch,since
This odd behavior of the barrier wave number does not affect the off-barrier wave numberk.To avoid questionable behaviors ofkBthe present study restricts the potential maximum and the scattering energy to be sufficiently small.Hence,ifm1>m2,implying the reduced mass satisfyingµ A plane wave of relative motion may be assumed propagating in the positivex-direction and then being re flected by a potential barrier,so that the stationary behavior asbecomes whereris the reflection amplitude andkthe asymptotic wave number.Part of the incoming wave penetrates the barrier region,and becoming the transmitted wave wheretis the transmission amplitude.The reflection coefficientRand the transmission coefficientTare defined by[7] NoteWhen considering the wave function describing the motion of both particles,sayψ1+ψ2,one needs a superposition of two waves traveling in opposite directions.Then one wave function,sayψ1,would be defined above and the other one,ψ2,defined by space-reflected boundary conditions.In this case interference effects occur,and the phases of the amplitudesrandtbecome important.Such considerations are ignored in the present study. The plane-wave solutions of the SRQ equations,and their derivatives,are fitted at the two boundary positionsx=±aof the rectangular barrier,yielding the transmission coefficient which is valid at all energiesϵ>0.Note in Eq.(14)that sin2for energiesϵ>V0turns into a sinh2-behavior forϵ The generalized Schr¨odinger(GS)equation for the two-body problem is given by:[2,4−5] where the variable coefficientis containing a two-body mass index This indexηGSappears only in the approximate theory and having numerical values in the range 1/4≤ηGS≤1,attaining the minimum value for equal masses;see Ref.[4]. Equation(15)is equivalent to the spinless Salpeter equation(SSE)introduced by Ikhdair in Ref.[2],and in earlier references therein.It has been applied by others;to scattering transmission[5]and to bound-state spectra.[6]It can for exponential-type potentials often be treated by transforming it to a standard differential equation of the hyper-geometric type.For the rectangular barrier case such transformations are not needed.The non-relativistic problem is covered by Eq.(16),where in(and inκBbelow in Eq.(19))one putsηGS=0. The generalized Schr¨odinger formula for the transmission(and reflection)coefficient would be similar to Eq.(14),but with different wave numbers.For notational simplicity the approximate wave numbers are denoted byκ(instead of e.g.kGS).Hence,the o ff-barrier GS-wave number is while in the barrier region one has The approximate transmission coefficient is given by The non-relativistic transition coefficient would be obtained from Eqs.(19)and(20)withηGS=0.The nonrelativistic transition coefficient does not show two-body effects and is not illustrated in the subsequent section. Results are presented in units such that1,wheremuis a mass unit.The length unit(xu=1)corresponds to the Compton wave lengthThe individual particle masses are denotedm1andm2in such mass units.One of the masses,m2,is determined in this study bym1and the reduced massµ.This choice of keeping the reduced mass as a primary mass parameter is motivated by the fact that non-relativistic results only depend on the reduced mass.The massm1is chosen to be the“large” mass so thatm1≥2µ. The two-body effects in this study have to do with the different mass combinations for the same reduced massµ.Equal masses are represented bym1=2µin the computations,and unequal masses are represented bym1=100µ. Transmission and reflection coefficients depend on the wave numbers in and off the barrier region.It is relevant to understand the approximate and exact wave numbers before a comparison of the transmission coefficients. The wave numberskBandκBseem analytically different.With the restricted conditiona numerical investigation of their squares shows that the approximate wave numberis a reasonably good approximation ofin a large range of realistic potential parameters. Fig.1 (Color online)Approximation errors in(blue curves)as function of ϵ/V0for V0= µ with µ =5,2,1,and 0.5 mass units.Solid lines represent unequal masses with m1=100µand dashed lines represent equal masses where m1=2µ.Hence,for equal massesRed lines correspond to errors of the non-relativistic wave numbers,for which ηGS=0 in the GS approximation.Hence,for equal masses the non-relativistic wave numbers are in best agreement with those of the semi-relativistic theory.For ϵ=V0all barrier wave numbers are in agreement. A potential barrier withV0=1µandµof the order of the relativistic mass unit(mu=1)shows good agreement betweenandTheir difference is plotted in Fig.1,againstϵ/V0.Dashed curves in Fig.1 represent equal masses and solid curves represent unequal masses for the same reduced mass.Red curves represent nonrelativistic wave numbers,obtained by puttingηGS=0 in the GS formulas. Errors in the GS barrier wave numbers increase significantly for unequal masses andV0(orµ)increasing beyond the unit mass.The GS approximation seems to be excellent for the equal-mass case(blue,dashed curves).The non-relativistic approximation is only valid for scattering energies close to the barrier top energy. For the same barriers as in Fig.1,the o ff-barrier wave numbers are studied in Fig.2.The non-relativistic(red curves)are accurate only nearϵ≈0 unless the reduced mass is much smaller than the relativistic mass unit.The GS-approximation improves the non-relativistic off barrier wave numbers significantly,although not as much as it improves the barrier wave numbers.The equal-mass cases(blue,dashed curves)in Fig.2 show no errors in the GS approximation. Fig.2 Approximation error in κ2(blue curves)as function of ϵ/V0for V0= µ with µ =5,2,1,and 0.5 mass units.Solid lines represent unequal masses with m1=100µ and dashed lines represent equal masses where m1=2µ.Red lines,tending to negative values as ϵ increases,correspond to errors of the non-relativistic wave numbers for which ηGS=0 in the GS formulas. Because of the relation between the transmission and reflection coefficients,T+R=1,it is sufficient to analyze just the transmission coefficientT.The formulas(14)and(20)indicate that the wave numbers play an important role.The over-barrier case of scattering energies allow oscillations depending on the barrier wave numbers and the barrier sizea.The o ff-barrier wave numbers affect the magnitudes of the amplitudes of the oscillations only,not the frequencies of the oscillations.For wide barriers,small errors in the barrier wave numbers may still be significant for the oscillation phases at energiesϵ≫V0. The error in the oscillation pre-factoris more difficult to understand.In Fig.3 the absolute error is denoted The parameters and energies used in Fig.3 are those taken as those in Figs.1 and 2.The error∆γfor the case of unequal masses(solid curves)changes sign and seems to be almost independent of potential and mass parameters,despite the significant differences due to parameters of the wave numbers in Figs.1 and 2.This error is singular in a transition region where the scattering energy is near the barrier top energy,and also close to the threshold limitϵ=0.Well inside the over-barrier and the under-barrier energy regions the errors are small.The singularities are cancelled by the fact thatκagrees withkasandagrees withasIn the barrier transition region there is a sign change inand in the oscillation pre-factorIn the same region one has which cancelsin the pre-factor and the over-all sign change.As a result of the apparent independence of∆γas potential parameters are changed,the main source of error in the transmission coefficient seems to be the argument of the sine function,4κBa,when this is real valued(overbarrier case).The spatial range of the potential magnifies the positive error inκBfora>1.The GS approximation predicts shorter energy periods of the possible oscillations inT,asϵ(>V0)increases.For scattering energies belowV0,Tis non-oscillatory and usually vanishing asϵ→0.The sine function has turned exponentially increasing asϵapproaches zero,whileV0being not too small.Errors inTare then less likely to be observed for the parameters used in Figs.1–3. Fig.3 Absolute GS-approximation error, in the oscillation pre-factor(Eq.(21))as function of ϵ/V0with V0=µandµ=5,2,1,and 0.5 mass units.The equal mass case(dashed line)does not show any significant numerical error. Fig.4 Transmission coefficients for a barrier range a=1,and other parameters being as in Figs.1–3.The equal mass cases are represented by dashed curves and the unequal mass cases represented by solid curves. Figure 4 shows the transmission coefficient for a barrier rangea=1 and for other parameters as in Figs.1–3.Two-body effects are signi ficant in all four subplots of Fig.4,although not forϵ≈V0.The GS-approximation results(surprisingly)agree with those of exact calculations(see Table 1),and results are represented by common curves.The dashed curves(m1=2µ)and solid curves(m1=100µ)differ slightly in their wavy behaviors.This is the two-body effect seen in Fig.4,which is well predicted by the GS-approximation. Figure 5 considers a three times wider barrier witha=3.Again,the results of the GS-approximation are in-distinguishable from the exact results on the scale of the figures.The two-body effects here,predictable by the GS-approximation,appear as shifts of transmission peaks for over-barrier energies.These shifts gradually increase as the energy increases. Table 1 shows numerical results for the transmission coefficient related to Fig.5 forµ=5,and selected values of the scattering energy.In this table results are compared with those of the GS-approximation.In the equal mass case(m1=2µ)in Table 1 both entries are identical.It can be con firmed(not included in the present work)that the transmission coefficientsTandTGSare analytically the same in the equal-mass case.For “light-heavy”masses the differences betweenTandTGSare still small on the graphical scales in Figs.4 and 5. The table,as well as Figs.4 and 5,show significant two-body effects for all system parameters,unless the transmission coefficient is exponentially small. Fig.5 Transmission coefficients for a barrier range a=3 and other parameters are as in Figs.1–3.The equal mass cases are represented by dashed curves and the unequal mass cases represented by solid curves. Table 1 Two-body transmission coefficients T and TGSare compared for selected scattering energies(ϵ/V0).The potential parameters are V0=1µ and a=3,and the results correspond to Fig.5,forµ=5. The rectangular potential allows exact numerical semirelativistic calculations,involving linear plane waves only and their matching at the barrier discontinuities.The generalized Schr¨odinger(GS)approximation seems to predict accurate energy behavior of the transmission coefficient in a reasonably realistic energy range.With the scales of the illustrations,the GS results are indistinguishable from those of the exact computations of the transmission coefficient and significant two-body effects are accurately obtained. Two-body effects in the present illustrations appear mainly as energy shifts of total transmission in the overbarrier energy region.These effects may seem more striking in numerical tables,like in Table 1,where in the overbarrier case oscillations may be dense on the energy scale and of quite large amplitudes;see Figs.4–5.In the underbarrier case two-body effects appear stronger for smaller values of the reduced mass(compare Figs.4 and 5). The observed accuracy of the GS approximation does not apply to the local wave numbers,but errors appear to cancel in the final formula for the transmission coefficient.In a more rigorous study on two-body interference effects,discussed in the final paragraphs of Sec.2,this situation may no longer prevail if the barrier energyV0is of the order ofm2c2or much larger. References [1]K.E.Thylwe,Phys.Scr.85(2012)065009;K.E.Thylwe,Eur.Phys.J.D66(2012)7. [2]S.M.Ikhdair and R.Sever Int.J.Mod.Phys.E17(2008)1107;Int.J.Mod.Phys.A20(2005)16509. [3]W.Lucha and F.F.Sch¨oberl,Int.J.Mod.Phys.A17(2002)2233;Int.J.Mod.Phys.A15(2000)3221,arXiv:hep-ph/9909451;Int.J.Mod.Phys.A14(1999)2309;Fizika B8(1999)193;Phys.Rev.A60(1999)5091,arXiv:hep-ph/9904391;Phys.Rev.A54(1996)3790;Phys.Rev.D50(1994)5443;Phys.Rev.D50(1994)5443. [4]K.E.Thylwe and S.Belov,arXiv:quant-ph/1508.02067. [5]S.Hassanabadi,M.Ghominejad,and K.E.Thylwe,Commun.Theor.Phys.63(2015)423. [6]S.Hassanabadi and A.A.Rajabi,Mod.Phys.Lett.A27(2012)1250057;S.Zarrinkamar,A.A.Rajabi,H.Hassanabadi,and H.Rahimov,Phys.Scr.84(2011)065008;S.Zarrinkamar,A.A.Rajabi,and H.Hassanabadi,Few-Body Sys.52(2011)165. [7]K.E.Thylwe,J.Phys.A:Math.Gen.38(2005)235.2.1 Scattering Boundary Conditions
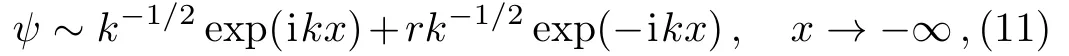
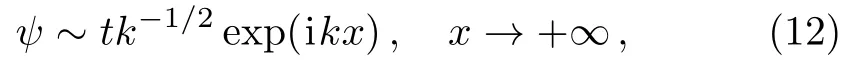
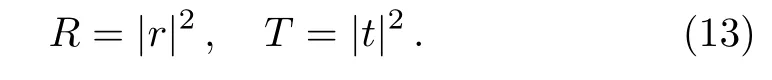
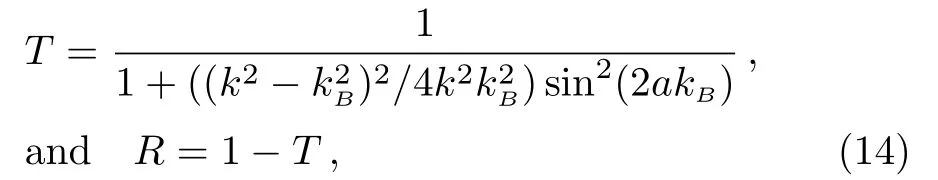
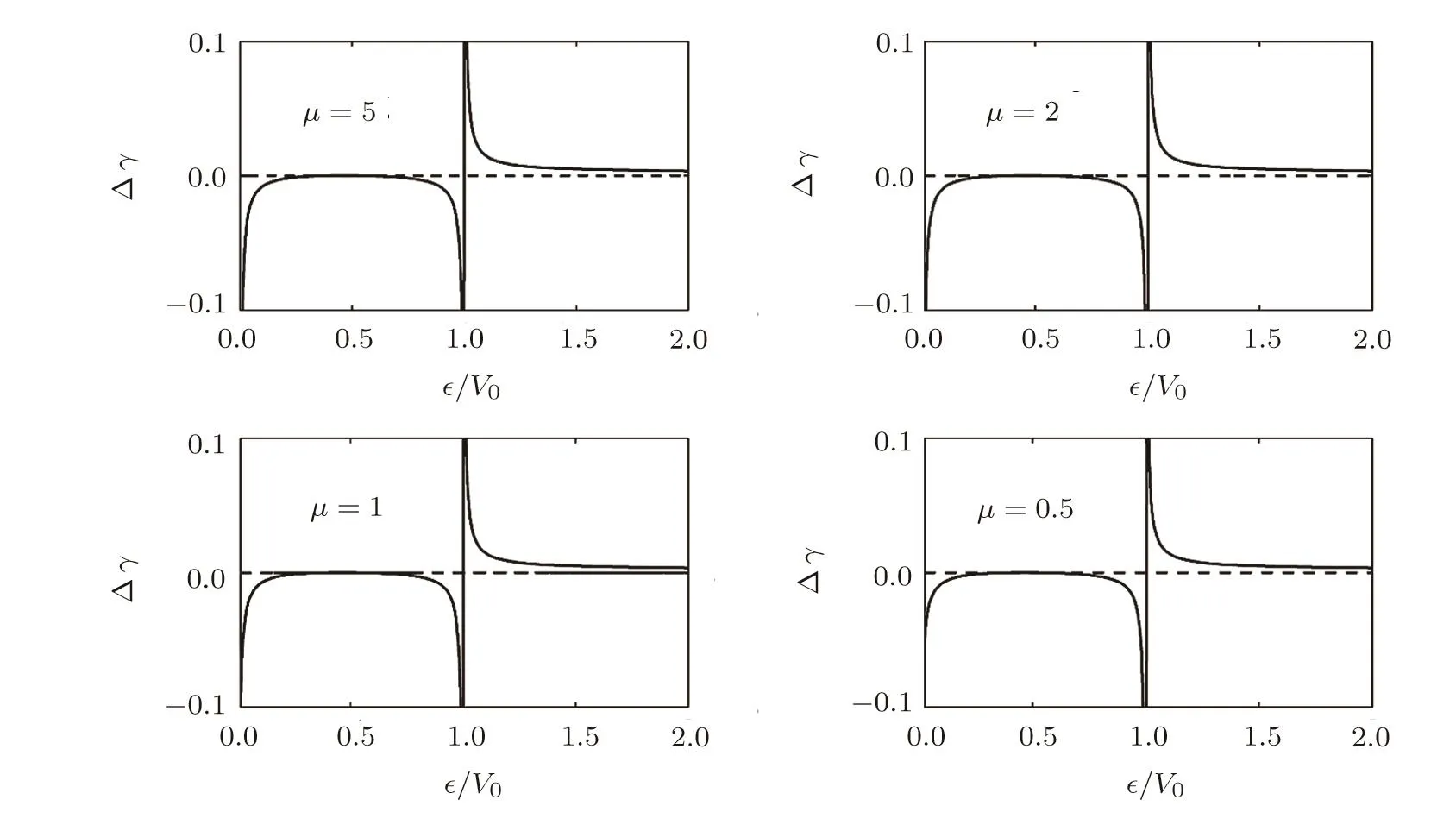
3 Generalized Schr¨odinger Method

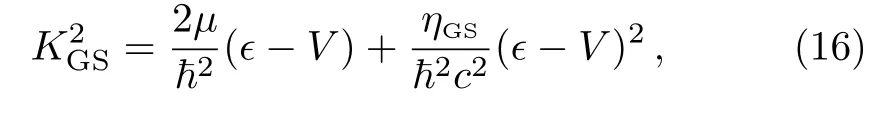
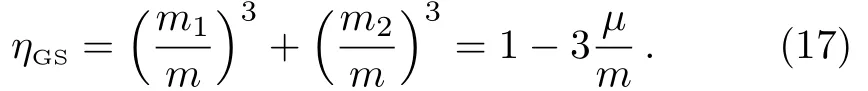
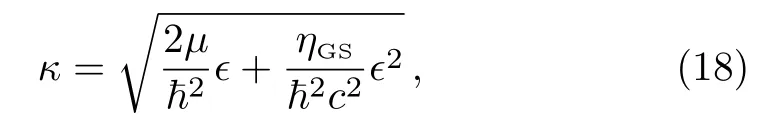
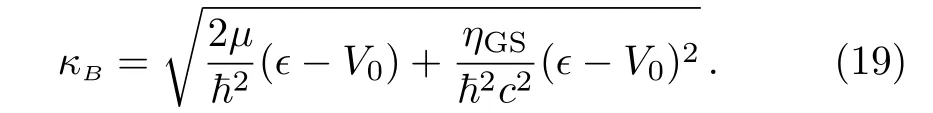
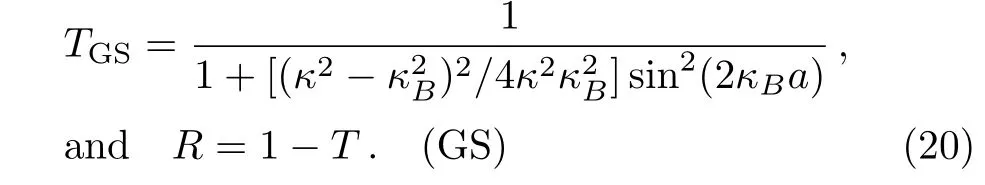
4 Results and Illustrations
4.1 Wave Numbers

4.2 Transmission Coefficient


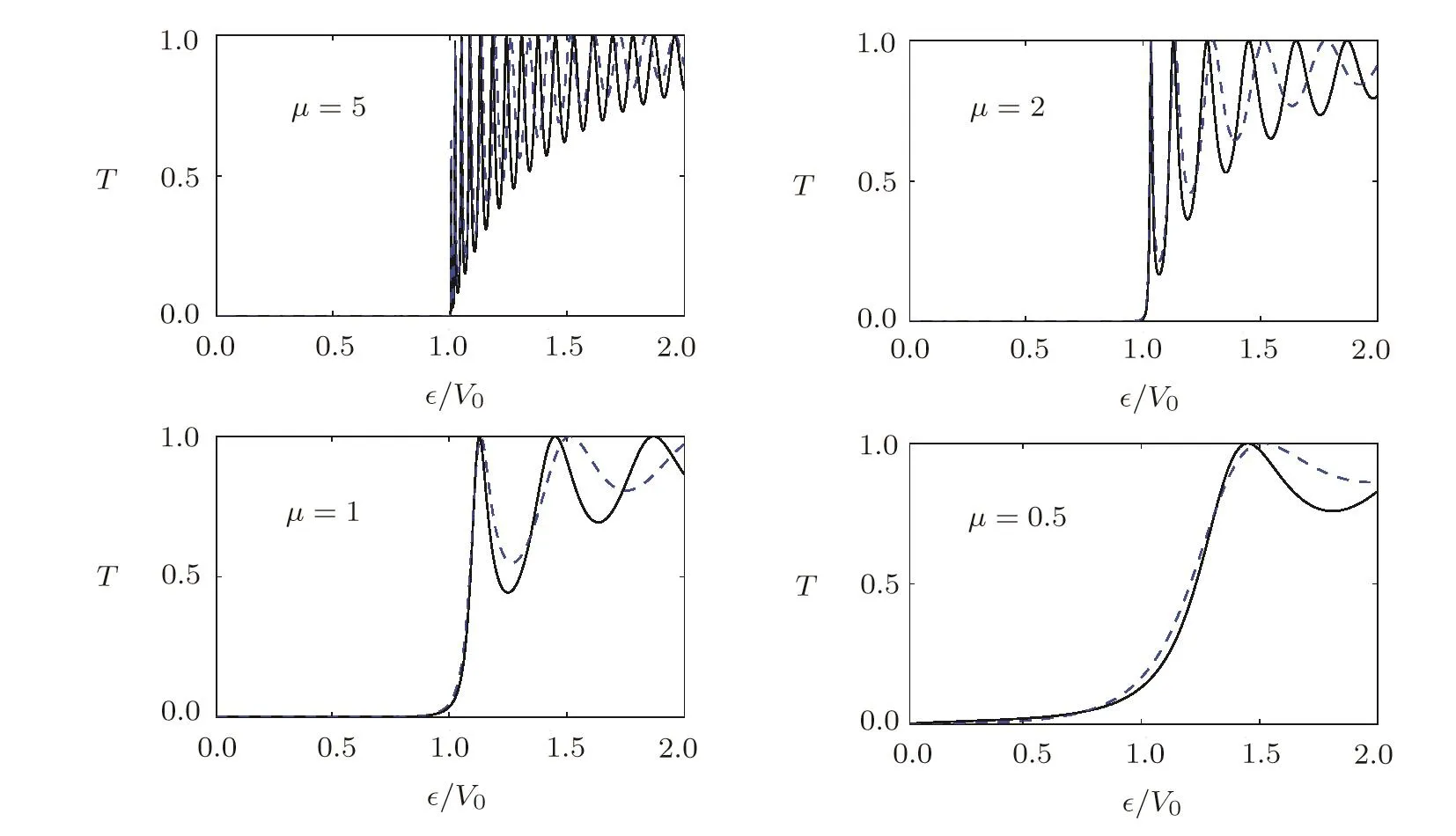

5 Conclusions
杂志排行
Communications in Theoretical Physics的其它文章
- Relativistic Correction on Neutrino Emission from Neutron Stars in Various Parameter Sets∗
- Study of Friction between Liquid Crystals and Crystalline Surfaces by Molecular Dynamic Simulations∗
- A Complex Network Model for Analyzing Railway Accidents Based on the Maximal Information Coefficient∗
- E ff ect of Mis fit Strain on Pyroelectric Properties of(111)Oriented Pb(Zr1−xTix)O3 Thin Films∗
- First-Principles Study of Structural,Magnetic,Electronic and Elastic Properties of PuC2∗
- Critical Behavior of Spatial Evolutionary Game with Altruistic to Spiteful Preferences on Two-Dimensional Lattices∗
