基于正弦调整的粒子群算法应用于换热网络

周　静,崔国民,彭富裕,肖　媛

(上海理工大学 新能源科学与工程研究所,上海　200093)



基于正弦调整的粒子群算法应用于换热网络

周静,崔国民,彭富裕,肖媛

(上海理工大学 新能源科学与工程研究所,上海200093)

摘要粒子群算法在优化换热网络综合问题后期,通常陷入局部极值而无法寻到全局最优解。通过对粒子群算法中的种群大小、迭代步数、最大速度、惯性权重4个参数的正交试验,得出了惯性权重是平衡算法局部搜索和全局搜索能力的一个重要因素。在综合分析标准PSO算法速度进化方程的基础上,提出了一种按正弦变化惯性权重的PSO算法,并利用标准测试函数验证了算法的性能。通过典型算例证明改进后的PSO对换热网络综合问题的有效性。

关键词粒子群算法;正交试验;正弦变化;换热网络综合

换热网络综合(Heat Exchanger Networks Synthesis,HENS)问题对过程系统的能量利用率和经济性具有重要的影响,该问题在本质上属于混合整数非线性规划模型(Mixed Integer Nonlinear Programming,MINLP)的范畴[1-2],其目标函数具有严重非凸、非线性的特性,导致其优化进程的不可持续且容易陷入局部最优解。

近年来,启发式方法的兴起使其在优化换热网络方面取得良好成效,这类算法主要有遗传算法[3-5]、模拟退火算法[6-7]、微分进化算法[8-9]、粒子群算法[10-11]等。粒子群算法(Particle Swarm Optimization,PSO)是由Kennedy 和Eberhart在1995年提出的一种模拟群体智能的优化算法[14]。为平衡PSO算法的探索和开发能力,本文首先对算法的参数进行正交试验而得到对算法性能影响较大的因子惯性权重,并在此基础上对其进行正弦动态变化,使粒子能够在一定的范围内实时获取更多的信息来调整自身的状态,增强PSO算法的全局搜索能力。

1换热网络数学模型

1.1换热网络问题描述

本文采用的换热网络模型为Grossmann提出的无分流分级超结构模型[12]。其中,换热网络级数表示为NK=max(NH,NC),最大换热器个数为NK×NC×NH。以一个5sp的案例为例,其包括2股热流体和3股冷流体,物流间的匹配关系如图1所示。

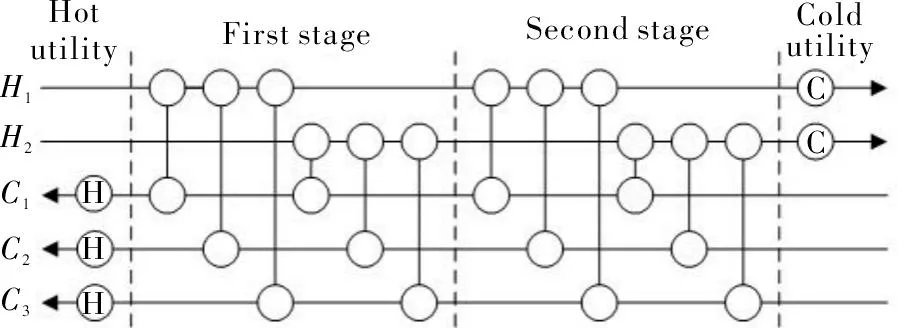
图1　换热网络分级超结构模型

1.2换热网络目标函数

换热网络将最小年综合费用作为优化问题的目标函数,式(1)为其数学表达式

(1)

其中,FEX为换热网络的固定投资费用;FHU、FCU为热、冷公用工程的年运行费用;FA为换热器的面积费用总和;k代表换热网络超结构模型的级数;i、j代表第股热流体与j第股冷流体;HU、CU代表热、冷公用工程;C0为换热器固定投资费用系数;C1为公用工程费用系数;C2为换热器面积费用系数;A代表换热器面积大小;Z代表换热器有无,有则取1,无取0。文献[13]对其热力学关系及约束给出了详细的解释。

2粒子群算法中参数的正交试验

PSO算法的特点是参数设置较少,不同的参数组合对PSO的优化效果有显著的影响[10]。采用正交试验法能合理有效的解决参数问题,以较少的试验次数得到一组较优的参数配置。

PSO算法主要参数为种群大小N,惯性权重ω,加速因子c1和c2,最大速度vmax,最大迭代次数K。其中,c1和c2有内在的联系,使c1=c2=0.5。下面对4个参数通过正交试验安排组合进行试验,上述因素都选用3水平,采用L4(23)的正交表,选Grossmann & Sargent (1978)文献[15]中的8sp1为例,结果如表1所示。

本文用方差分析方法[16],对数据进行分析,检验在一定假设条件下各组均值是否相等,由此判断因素各水平状态对试验指标的影响是否显著,得出对试验指标起重要作用的因素。

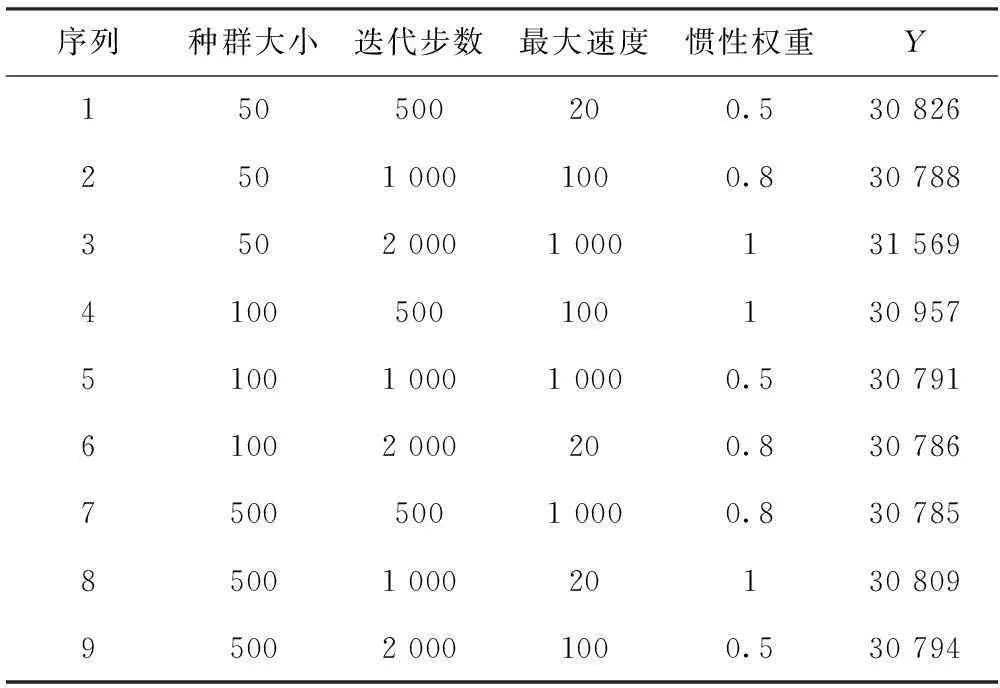
表1　正交试验表

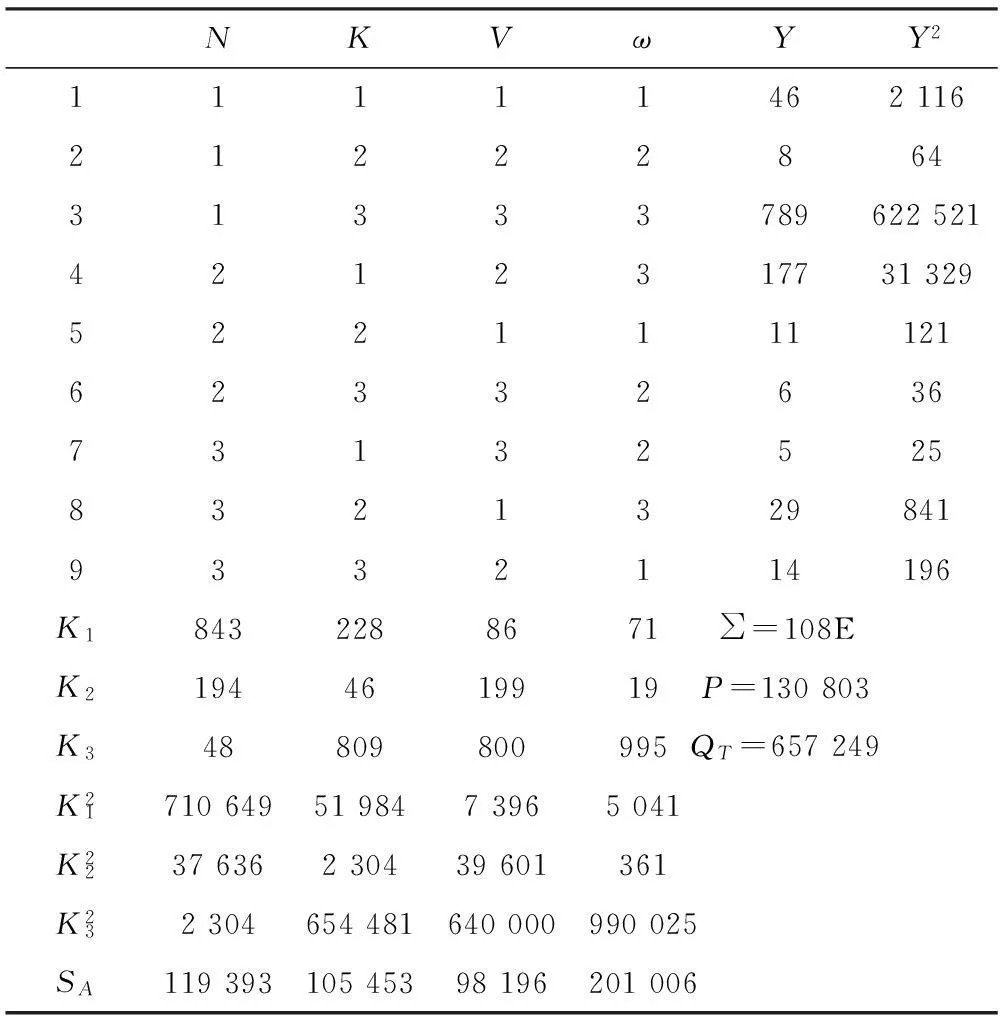
表2　试验结果方差分析表

注:为数据简单,表格中的Y都是减去常数30 780后的结果。

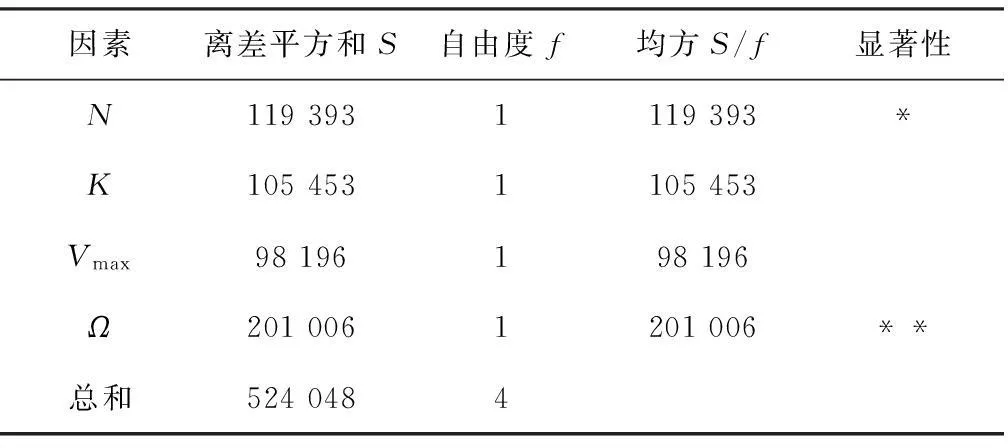
表3　显著性分析表

从方差分析表可看出,惯性权重对算法的影响效果最为突出。在单独研究惯性权重之前,先对另外3个参数的取值进行固定。此处令N=100,K=1 000,Vmax=1 000。

3正弦变化惯性权重的粒子群算法

在其他参数一致的基础上,来研究影响粒子群算法效果最显著的参数惯性权重ω。PSO算法的搜索过程是复杂非线性的,仅线性减小ω[17],结果只能收敛到局部极值点。本文提出一种非线性调整策略即正弦变化惯性权重的PSO,以此来研究粒子群算法的执行效果。

策略1(SIN-PSO)

ω=0.4+0.5sin(πiter/itermax)

(4)

该策略在算法执行早期,先让粒子进行自身最优点的寻求,当算法进行到一定程度后,开始重视粒子间的互相协作关系,使其都参与到最优信息的分享中,进行全局最优搜索,最后让最优的粒子进行局部搜索。

策略2(TSIN-PSO)

ω=0.4+0.5sin(10πiter/itermax)

(5)

在策略1的式子中,正弦函数的周期和幅值是需关注两个潜在的变量。合理选取周期可使粒子的搜索更细致、频繁,幅值的选取可改善探索能力。惯性权重的变化范围在[0.4,0.9]最为合适,为使其在幅值范围内逐步搜索更精细,将正弦函数的周期缩小为原来的10倍,此时函数如策略2所示。

由上式ω值的变化可知,在算法运行的整个过程中,ω值均在其区间范围内作周期性正弦变化,保证自身寻优与全局寻优同时动态进行。

4实验结果分析

为验证上述基于非线性正弦函数调整惯性权重的粒子群算法的性能,采用Griewangk 函数对其加以测试。

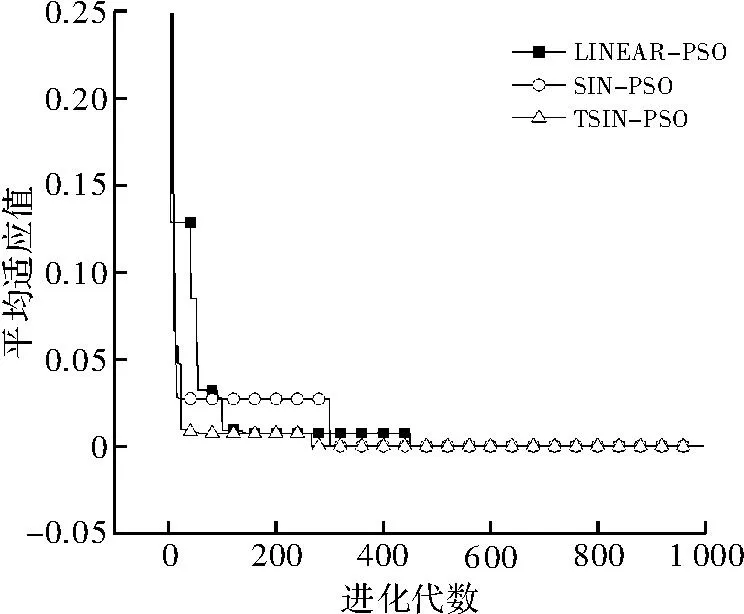
图2　Griewangk 函数图像

(6)

该函数的全局最优z(x,y)=0,(x,y)=(0,0)。分别用标准粒子群算法、SIN-PSO和周期改进策略的的TSIN-PSO算法对上述两个测试函数进行计算比较,其中标准PSO中的ω随着进化的进行从0.9线性减到0.4。对该测试函数的最优极小值进行求解,实验所得各测试函数平均最佳适应值进化对比情况如图2所示。通过3种惯性权重的适应度曲线对比可发

现:在相同的迭代次数下,TSIN-PSO算法的结果均优于标准粒子群算法和SIN-PSO算法,且其对于多峰高维函数也有较好的性能。

5换热网络算例分析

采用文献[18～21]的10sp算例进行验证,表4给出冷、热流体及公用工程的各参数。

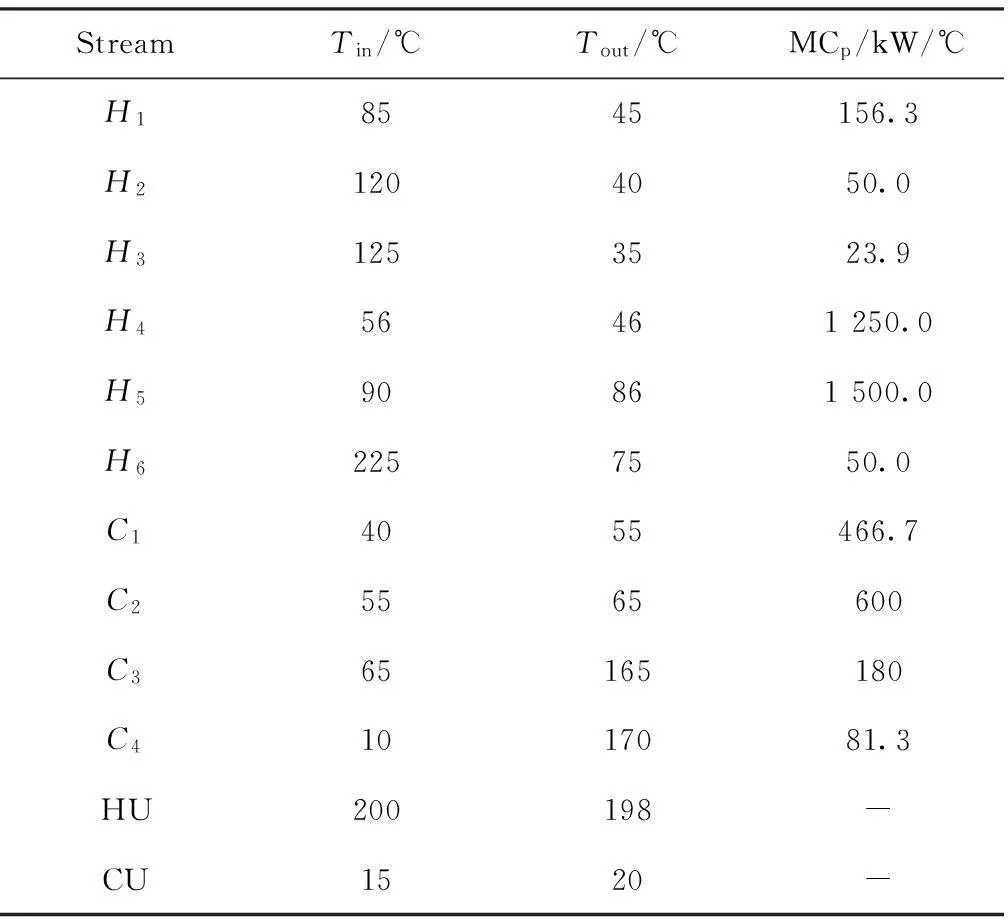
表4　算例1流股参数

换热器、冷却器和加热器的传热系数均为K=0.025 kW·(m2·℃)-1,费用计算公式均为60×A ＄·year-1;热公用工程费用为100 ＄·(kW·year)-1;冷公用工程费用为15 ＄·(kW·year)-1。

本文利用TSIN-PSO算法优化换热网络综合性能,优化得到的换热网络结构如图3所示,与其他文献结果相比如表5所示。通过本算例,充分说明了TSIN-PSO算法在解决换热网络的混合整数非线性规划问题方面有一定的优势,并能跳出其局部最优解,使优化精度更高,最终得到令人满意的优化结果。

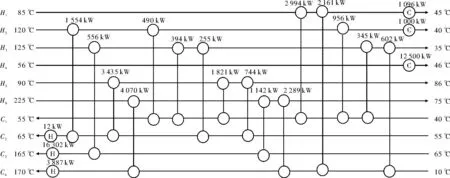
图3　算例10 sp优化结果

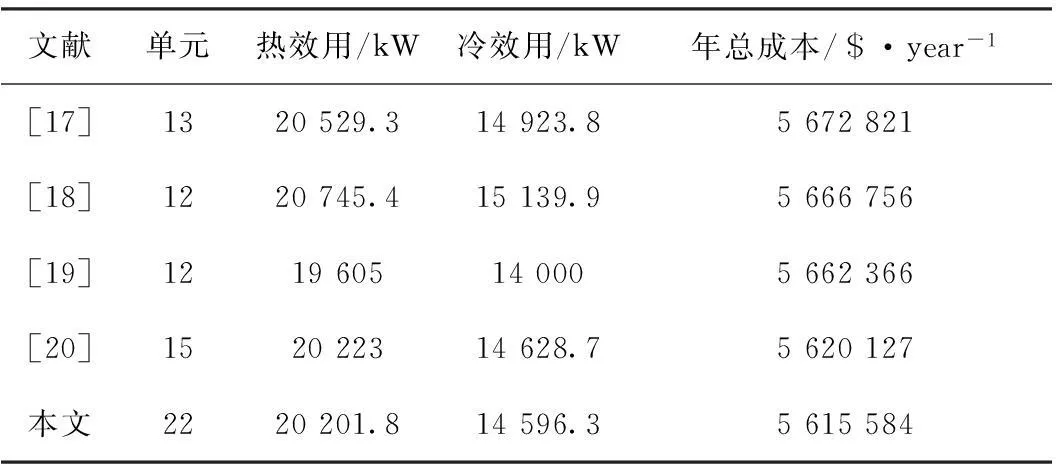
文献单元热效用/kW冷效用/kW年总成本/$·year-1[17]1320529.314923.85672821[18]1220745.415139.95666756[19]1219605140005662366[20]152022314628.75620127本文2220201.814596.35615584

6结束语

本文在标准粒子群算法基础上,以算法的参数分析为出发点,对参数进行正交试验得到在该算法中显著性最大的参数惯性权重。基于惯性权重的动态改进思想,提出一种基于惯性权重正弦调整的粒子群优化算法,并将正弦函数的周期性引入其中。通过两个典型函数的测试,其结果表明该方法在收敛速度和全局收敛性方面相比标准粒子群算法有一定的优势。最后,通过一个换热网络问题的实例进行验证,优化结果证明正弦改进的粒子群算法的有效性。

参考文献

[1]Furman K C,Sahinidis N V.A critical review and annotated bibliography for heat exchanger network synthesis in the 20th century[J].Industrial & Engineering Chemistry Research,2002,41(10):2335-2370.

[2]Morar Mihaela,Agachi Paul Serban.Review:important contributions in development and improvement of the heat integration techniques[J].Computers & Chemical Engineering,2010,34(8):1171-1179.

[3]Ravagnani M,Silva A P,Arroyo P A,et al.Heat exchanger network synthesis and optimisation using genetic algorithm[J].Applied Thermal Engineering,2005(25):1003-1017.

[4]Wang K F,Qian Y,Huang Q M,et al.New model and new algorithm for optimal synthesis of large scale heat exchanger networks without stream splitting[J].Computers & Chemical Engineering,1999(23):149-152.

[5]Brandt C,Fieg G,Luo X,Efficient synthesis of heat exchanger networks combining heuristic approaches with a genetic algorithm[J].Heat and Mass Transfer,2011(47):1019-1026.

[6]Athier G,Floquet P,Plbouleau L,et al.Process optimization by simulated annealing and NLP procedures.Application to heat exchanger network synthesis[J].Computers & Chemical Engineering,1997(21):475-480.

[7]Kirkpatric S,Gelatt C D,Vecchi M P,et al.Optimization by simulated annealing[J].Science,1983(220):671-680.

[8]Yerramsetty K M,Murty C V S.Synthesis of cost-optimal heat exchanger networks using differential evolution[J].Computers & Chemical Engineering,2008(32):1861-1876.

[9]Das S,Abraham A,Konar A.Particle swarm optimization and differential evolution algorithms:technical analysis,applications and hybridization perspectives[J].Study Computer Intellence,2008,116(3):1-38.

[10]Yan Lidi,Huo Zhaoyi,Yin Hongchao.Simultaneous synthesis of heat exchanger networks using particle swarm optimization[J].Chemical Industry Engineering Proceeding,2009(SI):439-442.

[11]He Qiaole,Cui Guomin,Xu Haizhu.Application of mimetic particle swarm optimization to continuous variable global optimization of cost-optimal heat exchanger networks[J].Petrochemical Technology,2014,43(1):37-45.

[12]Kennedy J,Eberhart R.Particle swarm optimization[C].Perth:IEEE International Conference on Neural Networks Proceedings,IEEE,1995.

[13]Fraser D M.The use of minimum flux instead of minimum approach temperature as a design specification for heat exchanger networks[J].Chemical Engineering Science,1989,44(5):1121-1127.

[14]Liu Z,Zhang J.An improved differential evolution algorithm for economic dispatch of power systems[J].Procedures Chinese Society of Electrical Engineering,2008,28(10):100-109.

[15]Grossmann I E,Sargent R W H.Optimum design of heat exchanger networks[J].Computers & Chemical Engineering,1978,2(1):1-7.

[16]Chen Kui.Design and analysis of experiments[M].Beijing:Tsinghua University Press,2005.

[17]Shi Y,Eberhart R C.A modified particle sws Fln optimizer[C].Anchorage:Proceeding IEEE International Conference on Evolutionary Computation,1998.

[18]Ravagnani M A,Silva A P,Arroyo P A,et al.Heat exchanger network synthesis and optimization using genetic algorithm[J].Application Thermy Engineering,2005,25(7):1003-1017.

[19]Yerram Setty K M,Murty C V S.Synthesis of cost—optimal heat exchanger networks using differential evolution[J].Computers and Chemical Engineering,2008,32(8):1861-1876.

[20]Mohammadhasani Khorasany R,Fesanghary M.A novel approach for synthesis of cost-optimal heat exchanger networks[J].Computers and Chemical Engineering,2009,33(8):1363-1370.

[21]Fang Dajun,Cui Guomin.Global optimization of heat exchanger networks using differential evolution algorithm[J].Journal of Chemical Industry and Engineering,2013,64(9):3285-3290.

Particle Swarm Optimization (PSO) with Sinusoidal Changing Inertia Weightfor Heat Exchange Network Synthesis

ZHOU Jing,CUI Guomin,PENG Fuyu,XIAO Yuan

(Research Institute of New Energy Science and Technology,University of Shanghai for Science and Technology,Shanghai 200093,China)

AbstractThe local optimum often arises when the Particle Swarm Optimization (PSO) optimization is used to optimize heat exchanger networks synthesis problems.The orthogonal experiments in population size,iterative steps,maximum velocity and the inertia weight show that the inertia weight is an important factor in the PSO improvement.Based on a comprehensive analysis of the standard PSO algorithm,this paper proposes a strategy of inertia weight according to the sinusoid.The performance of the algorithm is verified using the standard test functions.The presented case reveals the effectiveness of the proposed strategy in the heat exchange network synthesis.

Keywordsparticle swarm optimization;orthogonal experiment;sine change;heat exchanger network synthesis

中图分类号TP306.1

文献标识码A

文章编号1007-7820(2016)04-037-04

doi:10.16180/j.cnki.issn1007-7820.2016.04.010

作者简介:周静(1991—),女,硕士研究生。研究方向:化工过程系统优化。

基金项目:国家自然科学基金资助项目(51176125);上海市研究生创新基金资助项目(JWCXSL1301)

收稿日期:2015- 11- 13